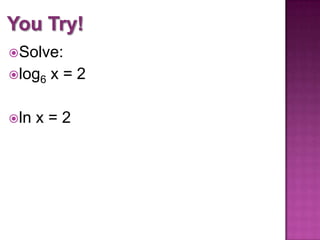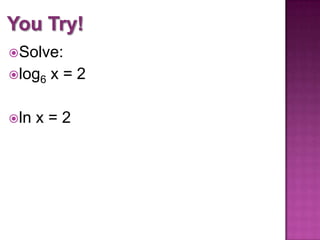
1. The document discusses rewriting logarithmic expressions, evaluating logarithms, and solving logarithmic equations. 2. It defines logarithms, introduces common (base 10) and natural (base e) logarithms, and explains how to "chop off the log" by rewriting logarithmic expressions in exponential form. 3. Examples are provided for evaluating logarithms and solving simple logarithmic equations.

1. Objectives:
1. Rewrite log equations
2. Evaluate logarithms
3. Solve log equations

2. know 22 = 4 and 23 = 8, but for
what value of x does 2x = 6?
It must be between 2 and 3…
Logarithms were invented to
solve exponential equations like
this.
x = log26 ≈ 2.585
We

3. Let
b and y be positive numbers
and b≠1.
The logarithm of y with base b is
written logby and is defined:
logby = x if and only if bx = y

4. Common
Logarithm - the log with
base 10
 log10 x = log x
Natural
Logarithm – the log with
base e
 loge x = ln x

5. Use the “circle cycle” to “chop off the
log!”
Write these in exponential form:
log2
32 = 5
log5 1
=0
log 10
=1
 ln
0.2 ≈ -1.6

6. To
find logb y, think
“b to what power will give me y?”
Examples:
log3
81
log1/2
log9
8
3

7. Find
log4
each logarithm:
64
log32
log
2
100

8. Find
the value of x to the nearest
hundredth:
10x = 170
ex
= 500

9. Solve
for x to the nearest
hundredth.
10x = 50
ex
= 50

10. To solve: rewrite in exponential
form, then simplify.
Solve without a calculator:
log5 x = 2
log
ln
x=2
|x| = 2

11. Solve:
log6
ln
x=2
x=2