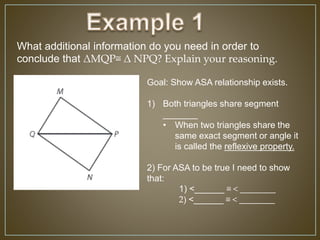
1) The document provides instructions for drawing triangles with specific side lengths and angle measures to demonstrate the ASA congruence criterion. It asks students to compare their triangles to see if they are congruent. 2) It explains that when a triangle has a side of a specific length and includes two particular angles, the ASA criterion guarantees all such triangles will be congruent. 3) The document then provides examples applying the ASA criterion to show two triangles are congruent, and asks what additional information is needed to show other pairs of triangles are congruent based on their corresponding parts.

1. QR for lesson

2. I would like to guarantee that the following triangles are
congruent.
Use whatever way you want to show if the triangles below are
or are not congruent. Remember what methods you used.

3. 1) On the back side draw a two inch line (use a pencil).
2) Draw two more lines to turn it into a triangle.
3) Compare you triangle with the people around you.
Can you guarantee that everyone in the room will have
the same triangle?

4. 4) Erase everything except for your two inch line.
5) Use the two inch line to create another line that will
form a 30° angle.
6) Draw one more line to form a triangle
7) Compare you triangle with the people around you.
Can you guarantee that everyone in the room will have
the same triangle?

5. 8) Erase the line that is NOT part of the 30°
9) Use the other side of the two inch line two creates a 40°
angle. Extend your line until they meet to form a triangle.
10) Compare you triangle with the people around you.
Can you guarantee that everyone in the room will have
the same triangle?
What do you notice?

6. Correspondin
g
Parts
Congruent
Triangles
Congruent
In order to show to triangles (or other figures) are congruent, you need
to show ALL the corresponding segments from both figures are
congruent and ALL the corresponding angles from both figures are
congruent.
While doing this can get repetitive, there are ‘tricks’ to help show
congruence. This is what we will study.

7. Objective: Use the ASA congruence
relationship to write and justify triangle
congruence.

8. When I gave you a side length and two angles in between the side
length, everyone should have created congruent triangles.
The reason is there is only ONE possible triangle that can be made
where a side is two inches and the angle in between is 30 and 40
degrees.
ASA (Angle-Side-Angle) triangle congruence happens
when two angles and the included side of one triangle is
congruent to two angles and the included side of another
triangle.

9. In ΔABC:
m<A = 30°
m<C = 40°
AC = 2’’
In ΔDEF:
m<D = 30°
m<F = 40°
DF = 2’’
By applying ASA ≅, ΔABC ≅ ΔDEF

10. What additional information do you need in order to
conclude that ΔMQP≅ Δ NPQ? Explain your reasoning.
Goal: Show ASA relationship exists.
1) Both triangles share segment
_______
• When two triangles share the
same exact segment or angle it
is called the reflexive property.
2) For ASA to be true I need to show
that:
1) <______ ≅ < ________
2) <______ ≅ < ________

11. What additional information do you need in order to
conclude that ΔMQP≅ Δ NPQ? Explain your reasoning.
How Mr.D. would answer this
questions if it was a homework, quiz,
or test question.
Since I know both triangles
share segment QP, I would
need to show that <MQP ≅ <
QPN and <MPQ ≅ <PQN. This
would allow me to say that
ΔMQP≅ Δ NPQ because of
ASA ≅

12. Point T is the midpoint of segment SU. What additional information do
you need in order to conclude that ΔRST≅ Δ VUT? Explain your
reasoning.
I know that segment _______ ≅ segment
______ because point T bisects segment SU.
I also know that <RTS ≅ <VTU because they are
__________ angles.
I would need to show that <RST ≅ <VUT. That
would show ΔRST≅ Δ VUT because of ASA ≅

13. What additional information do you need in order to
conclude that △SPR ≅△QRP? Explain your reasoning

14. Is there enough information in the diagram below to
say that the two triangles are congruent? Explain you
reasoning and draw a diagram to demonstrate.
No.
Even though two angles and a side from both triangles
are congruent, the triangle on the right shows ASA,
while the triangle on the left does not. This is not
enough to determine congruence.

15. ASA congruence in ebackpack. Do only #1-3
For full credit, make sure you completely explain your
reasoning like we did in the examples.