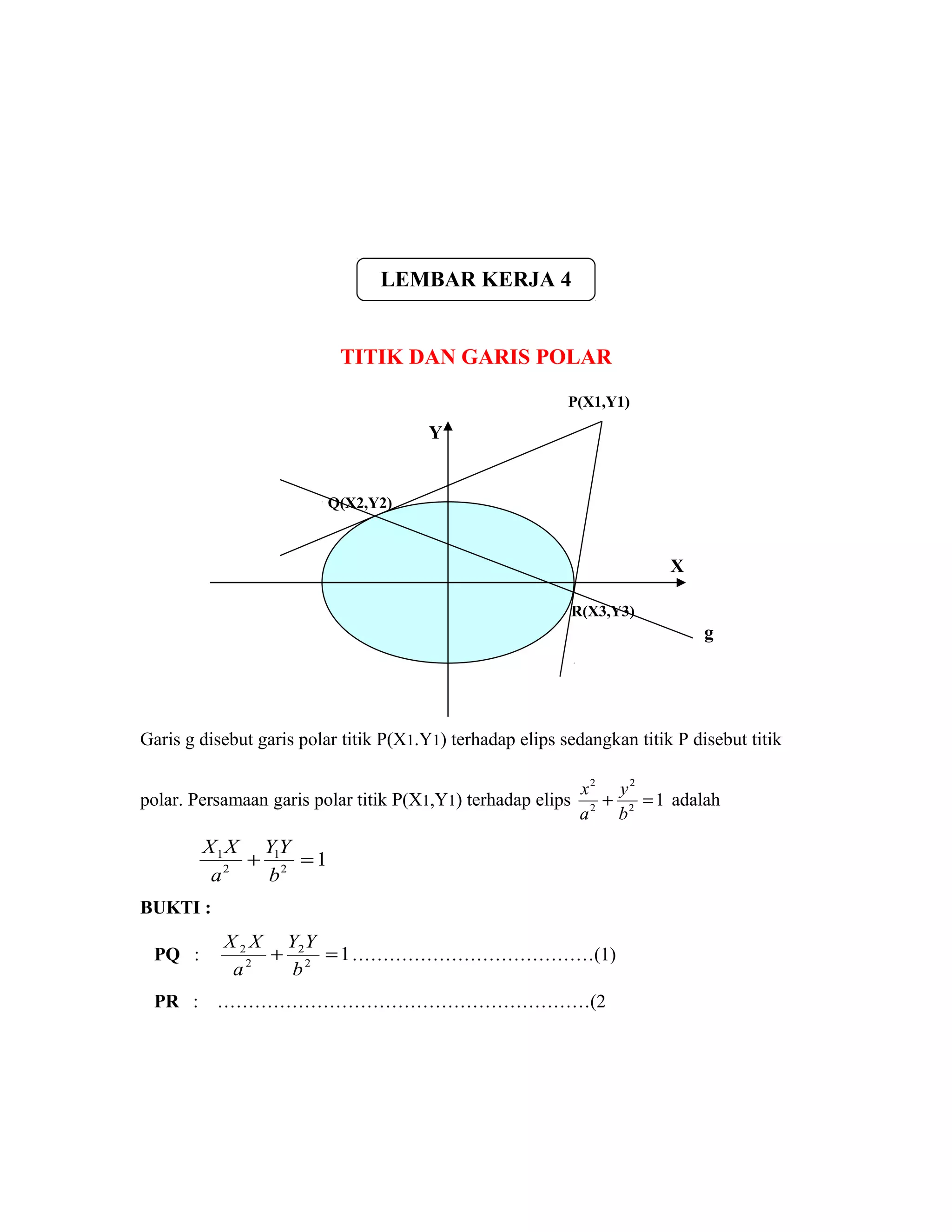
Dokumen ini membahas tentang konsep elips dalam geometri analitik, termasuk definisi, persamaan elips, serta metode untuk menentukan pusat, fokus, dan sumbu. Selain itu, ada penjelasan mengenai garis singgung, normal, dan garis polar terhadap elips, serta latihan soal yang menguji pemahaman konsep tersebut. Sebagian besar materi diorganisir dalam lembar kerja yang interaktif untuk membantu pemahaman siswa.

1. MATERI
Oleh :
Oktiana Dwi P H
NIM: 20082012012
MATA KULIAH
GEOMETRI ANALITIK BIDANG
DAN RUANG
PERSAMAAN ELIPS DAN GARIS
SINGGUNG ELIPS

2. ELIPS
Definisi elips :
Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya terhadap dua titik
tertentu tetap harganya.
Dua titik tertentu tersebut dinamakan titik fokus ( F 1 dan F 2 ) . Titik C, P dan Q
ada pada elips, maka berdasarkan definisi elips di atas diperoleh :
CF1 + CF 2 = PF1 + PF 2 = QF1 + QF 2
Q
P
C
F1
F 2
LEMBAR KERJA 1

3. PERSAMAAN ELIPS
1. PERSAMAAN ELIPS DENGAN PUSAT O(0,0)
Misal titik F1(-c,0) dan F2 (c,0)
Titik A(-a , 0) ada pada elips maka AF1 + AF2 = ……….. + …………..= …………..
Titik C (0,b) ada pada elips maka CF1 + CF2 = ……………..
CF1 = CF2 =……………
Sesuai definisi elips :
Apabila P ( x , y ) ada pada elips maka PF1 + PF2 = 2a, maka :
Ellips = { P | PF1 + PF2 = 2a }
= { (x,y) | √ (( x+c )² + y²) + √ ((x-c)² + y²) = 2a }
= { (x,y) | √ (( x+c )² + y²) = 2a - √ ((x-c)² + y²) }
= { (x,y) | ………………………………………............................................... }
= { (x,y) | …………………………………………………………………….. ..}
= { (x,y) | ……………………………………………………………………… }
= { (x,y) | ……………………………………………………………………….}
= { (x,y) | ……………………………………………………………………….}
( dari gambar diperoleh a² - c² = b² )
Ellips = { (x,y) | …………………………} atau { (x,y) | 2
2
a
x
+ 2
2
b
y
= 1 }
A(-a,0) B(a,0)
C (o,b)
F1(-c,0) F2( c,0)
P(x,y)
Y
X
a a
D(0,-b)
O

4. Jadi Persamaan Elips dengan pusat (0,0) adalah { (x,y) | 2
2
a
x
+ 2
2
b
y
= 1 }
Catatan :
1. Titik A, B, C dan D disebut titik puncak elips.
2. A(-a,0) , B(a,0) dan AB disebut sumbu mayor /sumbu panjang (panjangnya = 2a)
3. C(0,b) , D(0,-b) , CD disebut sumbu minor / sumbu pendek ( panjangnya = 2b )
4. Dari gambar terlihat bahwa a 2
= b 2
+ c 2
2. PERSAMAAN ELIPS DENGAN PUSAT (p,q)
Jika pusat elips adalah titik P(p,q) dan melalui titik ini dibuat garis-garis sejajar sb x dan
sb y ( yang dinamakan x’ dan y’), maka terdapat hubungan :
x = p + x’ atau x’ = x - p dan y = q + y’ atau y’ = y – q
Terhadap sistem koordinat bersumbu X’ dan Y’ persamaan elips adalah :
……………………………………..
Dengan substitusi hasil pergeseran sumbu diperoleh persamaan elips berpusat di P(p,q) :
………………………………………
Jadi Persamaan Ellips dengan pusat P(p,q) adalah
x’
y’
Y’Y
T(x,y)
F2(p+c,q)F1(p-c,q) P(p,q)
X’
XO

5. { (x,y) | …………………………………………………. }
LATIHAN
1. Diketahui persamaan elips :
1
9
)4(
25
)2( 22
=
−
+
+ yx
Tentukan :
a. Koordinat pusat.
b. Koordinat fokus.
c. Koordinat ke empat titik ujung sumbu elips
2. Tentukan persamaan elips apabila diketahui koordinat titik fokusnya (-6,2) dan (2,2)
serta salah satu koordinat titik puncaknya adalah (3,2)
3. Kalau sumbu panjang suatu elips berimpit dengan sb x dan panjang kedua sumbunya
berturut-turut 10 dan 6 , sedangkan elips itu menyinggung sb y , tentukan persamaan
elips tersebut!

6. DIREKTRIX DAN EKSENTRISITET
Elips juga didefinisikan sebagai tempat kedudukan titik-titik yang perbandingan jarak ke
suatu titik tertentu dan suatu garis tertentu tetap harganya yaitu antara 0 – 1
Titik tertentu disebut titik fokus dan garis tertentu disebut direktrix.
Titik fokusnya adalah titik F (-c,0) dan G (c,0) serta garis f dan g disebut garis direktrix
Dari gambar di atas maka diperoleh :
p 2
= ………………………….. = ………………………………………..
q 2
= ……………………………= ………………………………………..
p 2
- q 2
= …………………..
( p – q ) ( p + q ) = ………………
( p – q ) (……..) =………………
( p – q ) = ………………
( p – q ) = …………………………….
( p + q ) =…………………………...... +
………. =…………………………….
( p – q ) = ……………………………
( p + q ) =…………………………...... -
Y
X
g
X
f
p q
F G
P(X0,Y0)
O
LEMBAR KERJA 2

7. ……… = ……………………………...
Diperoleh :
P =……………
q = ……………
Jadi :
p : (……………..) = ………... ( perbandingan jarak dari titik P ke titik fokus F
dengan jarak dari titik P ke garis f =
a
c
)
q : (……………..) = ……....... ( perbandingan jarak dari titik P ke titik fokus G
dengan jarak dari titik P ke garis g =
a
c
)
Artinya :
1. Jarak dari titik P ke garis f adalah …………
Jadi f : x = ……
2. Jarak dari titik P ke garis g adalah …………
Jadi g : x = …….
Jadi :
Perbandingan jarak dari titik P ke titik F dan jarak dari titik P ke garis f = perbandingan
jarak dari titik P ke titik G dan jarak dari titik P ke garis g =
a
c
Catatan :
Garis f dan garis g disebut garis direktrix dan harga
a
c
disebut eksentrisitet
SOAL LATIHAN :
1. Diketahui persamaan elips :
1
9
)4(
25
)2( 22
=
−
+
+ yx
Tentukan :
a. Persamaan direktrix elips
2. Tentukan persamaan elips dengan pusat
(1,2) dan eksentrisitet 4/5 , sedangkan
direktrixnya 4x = 25

8. b. Eksentrisitet
GARIS SINGGUNG PADA ELIPS
1. PERSAMAAN GARIS SINGGUNG ELIPS DENGAN GRADIEN TERTENTU
Misal ada garis g : y = mx + n…………………………(1)
Dan elips : 2
2
a
x
+ 2
2
b
y
= 1 ……………………….(2)
Maka jika garis g (1) dipotongkan terhadap elips (2) maka diperoleh :
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
Dari persamaan di atas didapat :
D = …………………………………
= …………………………………
= …………………………………
= …………………………………
= …………………………………
Jika garis g menyinggung elips maka D = 0
……………………………………. = 0
…………………………………… = 0
n 2
=……………………………
n = ……………………………
LEMBAR KERJA 3

9. Jadi diperoleh persamaan garis singgung elips 2
2
a
x
+ 2
2
b
y
= 1 dengan gradien m adalah:
y = ………………………..
2. PERSAMAAN GARIS SINGGUNG ELIPS DI TITIK S ( X 1 , Y 1 )
Titik S ( X1 , Y1 ) pada elips, maka :
12
2
1
2
2
1
=+
b
Y
a
X
⇔ 222
1
22
1
2
baYaXb =+ ………………..(1)
Titik ( X2 , Y2 ) pada elips maka :
12
2
2
2
2
2
=+
b
Y
a
X
⇔ 222
2
22
2
2
baYaXb =+ ………………(2)
Titik ( X3 , Y3 ) pada elips maka :
12
2
3
2
2
3
=+
b
Y
a
X
⇔ 222
3
22
3
2
baYaXb =+ ………………(3)
Jika (2) dikurangi (3) maka diperoleh :
………………………………………………..
…………………………………………………
………………………………………………..
…………………………………………………
X
Y
S
S’
S(X1,Y1)
O
(X2.Y2)
(X3,Y3)

10. …………………………………………………
32
32
XX
YY
−
−
=
)(
)(
32
2
32
2
YYa
XXb
+−
+
Jadi gradien garis s’ adalah:
)(
)(
32
2
32
2
YYa
XXb
+−
+
Karena s // s’ maka gradien garis s adalah :
)(
)(
32
2
32
2
YYa
XXb
+−
+
Pada saat s merupakan garis singgung maka ( X2 , Y2 ) = ( X3 , Y3 ) = ( X1 , Y1 )
sehingga gradien garis s = …………….. = ………………… = …………………
Jadi persamaan garis singgung di S ( X1 , Y1 ) adalah :
………………………………………….
………………………………………….
………………………………………….
Sehingga diperoleh :
……………………………………………
……………………………………………
Atau
………………………………………….
Jadi persamaan garis singgung elips 2
2
a
x
+ 2
2
b
y
= 1 di titik S ( X1 , Y1 ) adalah :
……………………………………………
Dengan cara yang sama maka persamaan garis singgung pada elips

11. 2
2
2
2
)()(
b
qy
a
px −
+
−
= 1 di titik ( X1 , Y1 ) adalah :
…………………………………………………………..
SOAL LATIHAN :
1. Tentukan persamaan kedua garis singgung pada elips 16x 2
+25y 2
= 400
yang sejajar dengan garis 3x + y +1 = 0
2. Tentukan persamaan garis singgung elips 16x 2
+ 25y 2
+ 160x – 150y +
225 = 0 di titik yang berabsis 0.

12. PERSAMAAN GARIS NORMAL PADA ELIPS
Persamaan garis singgung elips di titik (X1,Y1) adalah:
12
1
2
1
=+
b
YY
a
XX
Maka :
X
Ya
Xb
Y
1
2
1
2
−=
Jadi gradien garis singgung elips di (X1,Y1) adalah :
1
2
1
2
Ya
Xb
−
Maka gradien garis normal (garis yang melalui titik singgung dan tegak lurus garis
singgung) adalah :
1
2
1
2
Xb
Ya
Jadi persamaan garis normal elips di titik (X1,Y1) adalah :
)( 1
1
2
1
2
1 XX
Xb
Ya
YY −=−

13. M
A
T
E
R
I
TITIK DAN GARIS POLAR
ELIPS
MATA KULIAH
GEOMETRI ANALITIK BIDANG DAN
RUANG

14. TITIK DAN GARIS POLAR
Garis g disebut garis polar titik P(X1.Y1) terhadap elips sedangkan titik P disebut titik
polar. Persamaan garis polar titik P(X1,Y1) terhadap elips 12
2
2
2
=+
b
y
a
x
adalah
12
1
2
1
=+
b
YY
a
XX
BUKTI :
PQ : 12
2
2
2
=+
b
YY
a
XX
…………………………………(1)
PR : ……………………………………………………(2
LEMBAR KERJA 4
Y
X
R(X3,Y3)
Q(X2,Y2)
P(X1,Y1)
g

15. P ( X 1 ,Y 1 ) pada PQ maka : ………………………………………..(3)
P ( X 1 ,Y 1 ) pada PR maka : ………………………………………...(4)
Perhatikan (3) dan (4) ternyata titik Q(X2,Y2) dan R(X3,Y3) terletak pada garis :
………………………………………
Maka persamaan garis polar titik P (garis g) adalah :
…………………………………………
…………………………………………
SOAL LATIHAN :
1. Buktikan, bahwa ketiga garis polar
titik-titik (2,5/2) , (-4 , 10), dan (8,-5)
terhadap elips 5x 2
+ 4y 2
= 20
melalui sebuah titik tertentu. Titik
manakah itu?
3. Diketahui elips dengan persamaan 25x
2
+ 16y 2
- 50x - 32y – 359 = 0
Tentukan =
a. Koordinat pusat
2. Tentukan titik polarnya garis
2x – 3y = 12 terhadap elips
1
46
22
=+
yx
4. Diketahui elips
yxyx 284 22
−++ +1 = 0.
Tentukan koordinat titik potong garis
y = x dengan elips tersebut.

16. b. Koordinat kedua titik fokus
c. Koordinat titik puncak
d. Panjang sumbu mayor dan
panjang sumbu minor
DUA GARIS TENGAH SEKAWAN
k : y = m x
garis-garis yang sejajar k mempunyai persamaan
y = m x + n …………………(1)
garis (1) memotong elips 12
2
2
2
=+
b
y
a
x
maka diperoleh :
……………………………………………..
Sehingga :
S
X
Y
R
Q(X2,Y2)
P(X1,Y1)
B A
T
M
l
k=mx

17. X1 + X2 = ………………..
Jika titik T merupakan titik tengah talibusur antara kedua titik potong maka :
XT = …………………………………………………………………
Dan
YT = ………………………………………………………………..
= ………………………………………………………………..
Jadi garis yang melalui T ( XT , YT ) adalah :
y = ……………………………………………… …………..(2)
Garis tersebut merupakan garis lurus dan dinamakan garis l yang melalui titik O(0,0)
Garis-garis k dan l disebut dua garis tengah sekawan suatu elips, yang satu merupakan
tempat kedudukan titik-titik tengah semua tali busur yang sejajar dengan garis lainnya.
k : y = mx
l : y = - x
ma
b
2
2
hasilkali kedua koefisien arah dari dua garis tengah sekawan adalah tetap yaitu :
m . 





−
ma
b
2
2
= 2
2
a
b
−

18. Misal kedua garis tengah sekawan elips adalah PQ dan RS dengan P(X1,Y1)
P(X1,Y1) ada pada elips maka :
222
1
22
1
2
2
2
1
2
2
1
1
bayaxb
b
y
a
x
=+
=+
Koefisien arah PQ adalah :
1
1
x
y
mPQ . mRS = - 2
2
a
b
mRS = - 2
2
a
b
1
1
y
x
maka persamaan garis RS adalah :
Q
S
R
P(X1,Y1)l
k

19. Y = - X
ya
xb
1
2
1
2
Perpotongan RS dengan elips menghasilkan :
22
2
1
2
1
2
222
bax
ya
xb
axb =




 −
+
( ) 2
1
422
1
22
1
2
yaxxbya =+
Maka diperoleh :
b
y
a
x
yaxba
1
2
1
4222
±=
=
Dengan jalan yang sama maka diperoleh:
a
x
b
y
dan
a
x
b
y
b
y
a
x
dan
b
y
a
x
jadi
a
x
b
y
sr
sr
11
11
1
:
−==
=−=
±=
SOAL LATIHAN :

20. 1. Buktikan, bahwa ketiga garis polar titik-titik (2,5/2) , (-4 , 10), dan (8,-5) terhadap
elips 5x 2
+ 4y 2
= 20 melalui sebuah titik tertentu. Titik manakah itu?
2. Tentukan titik polarnya garis
2x – 3y = 12 terhadap elips 1
46
22
=+
yx