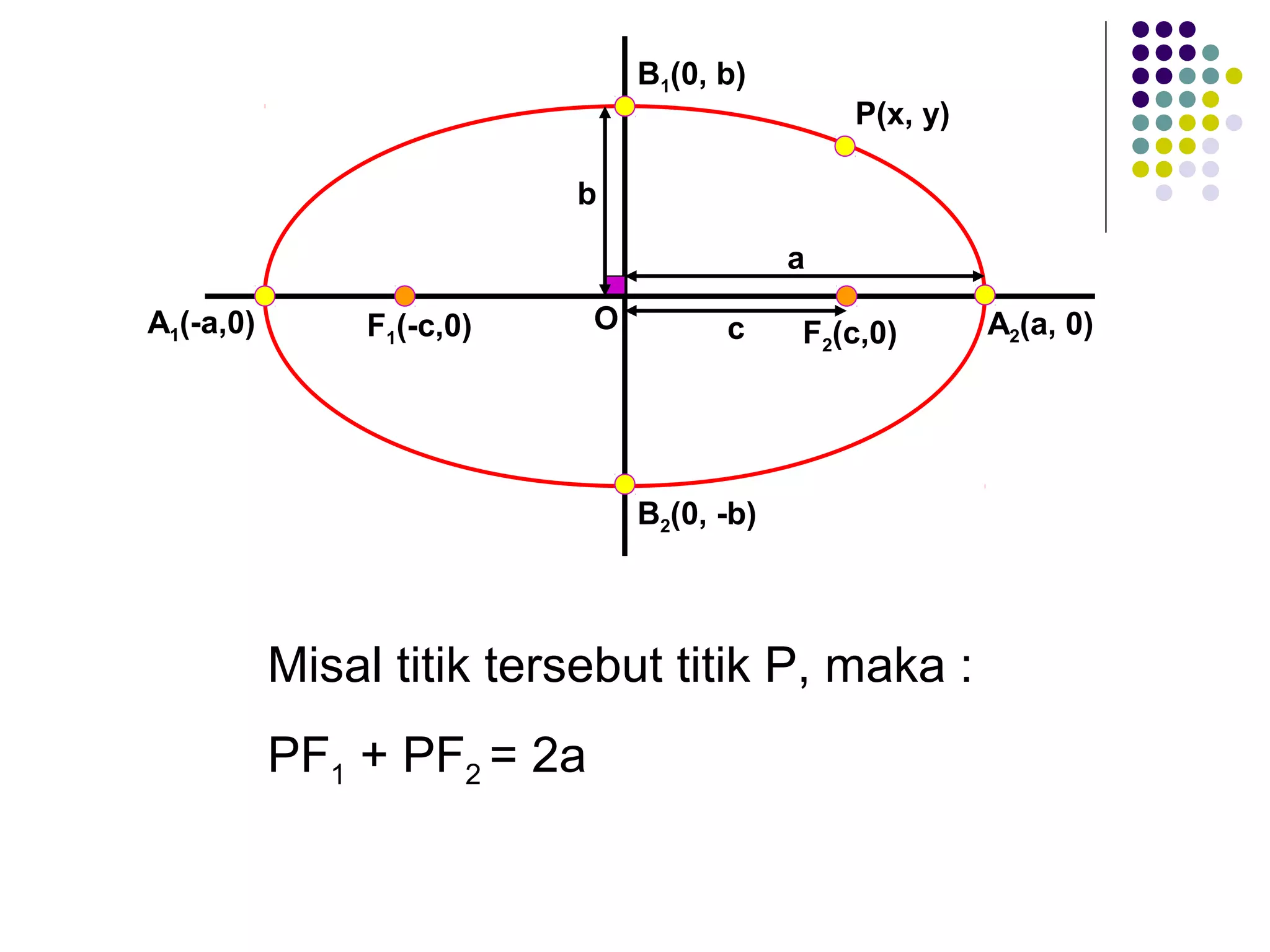
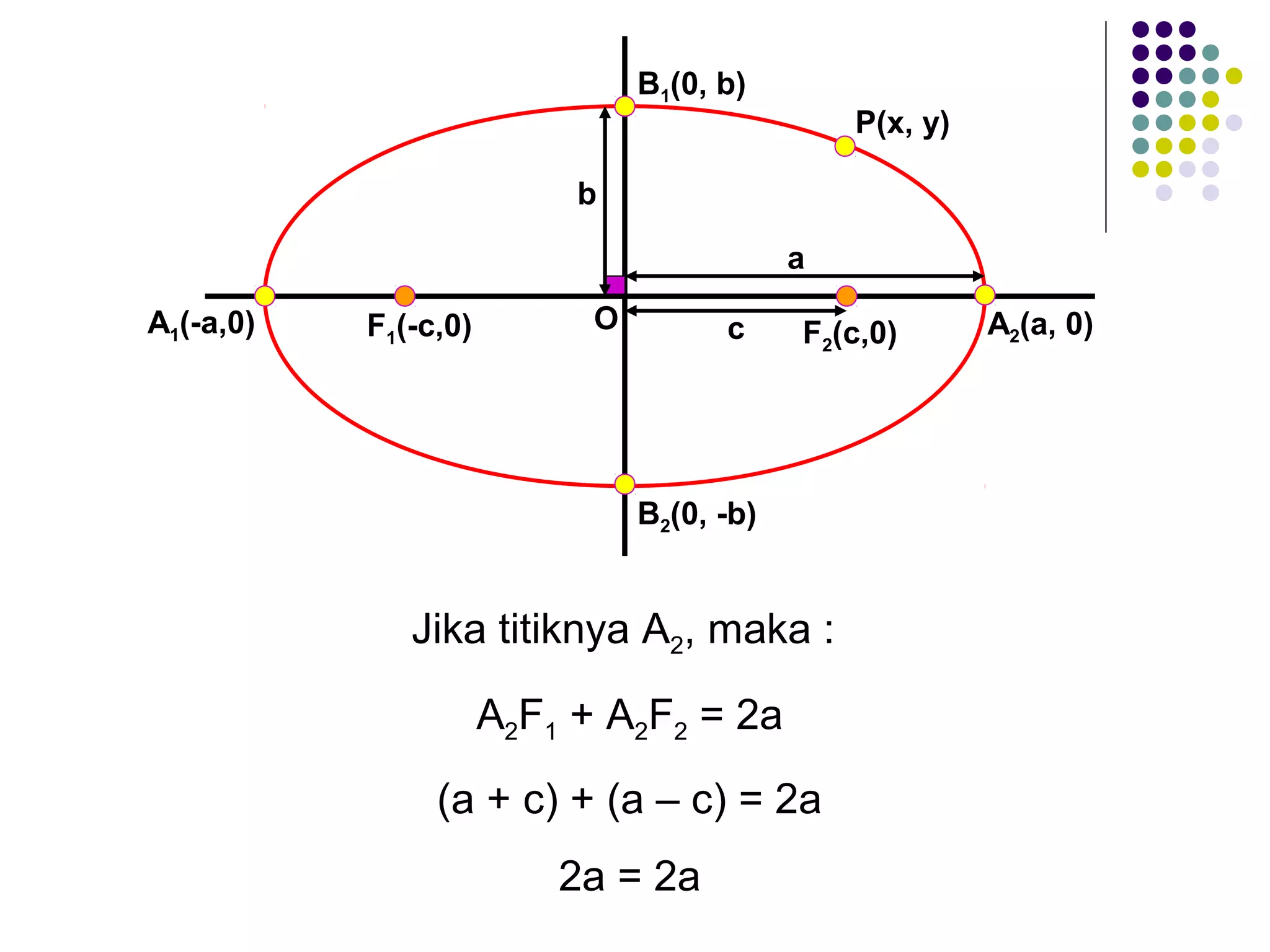
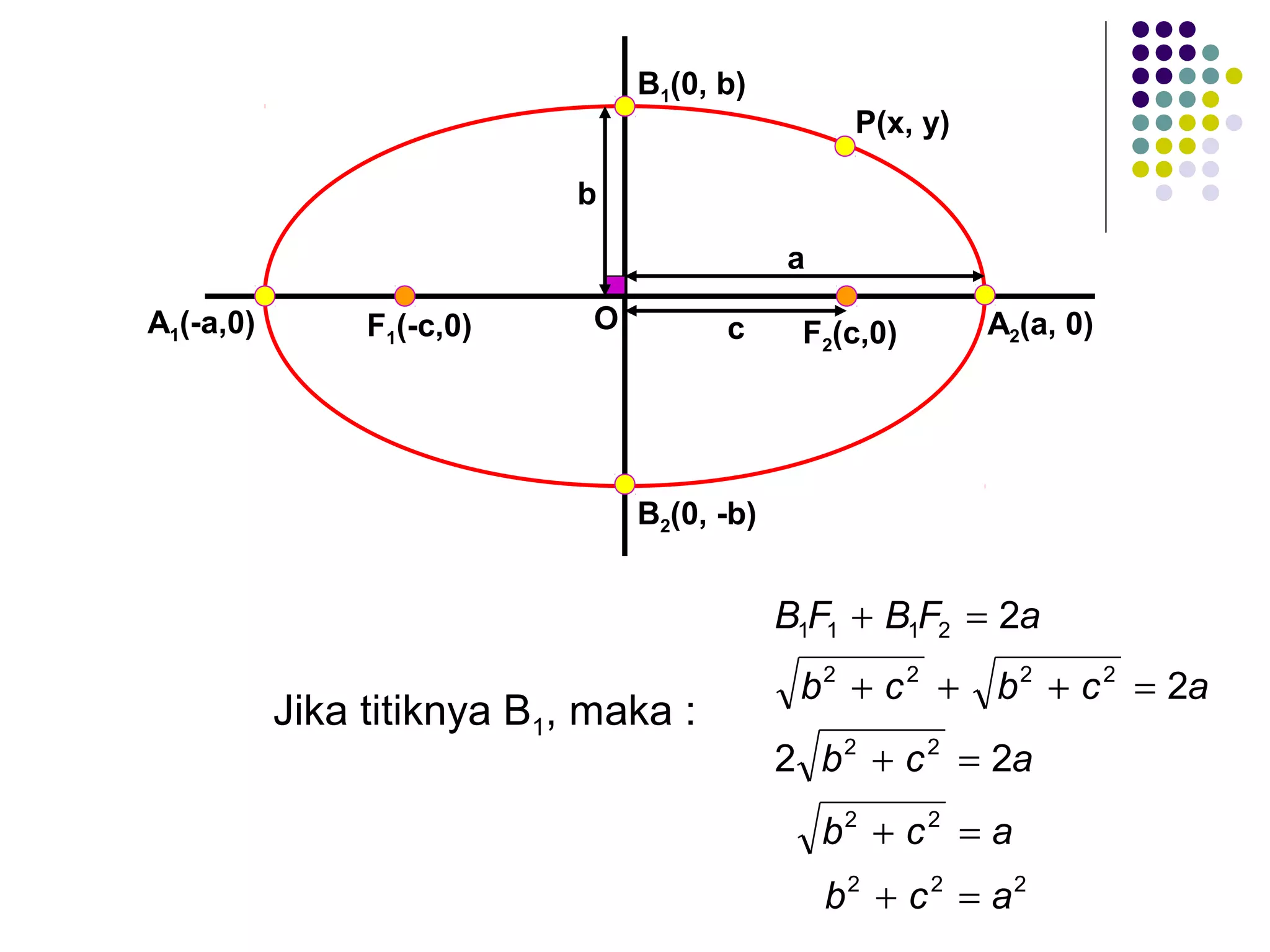
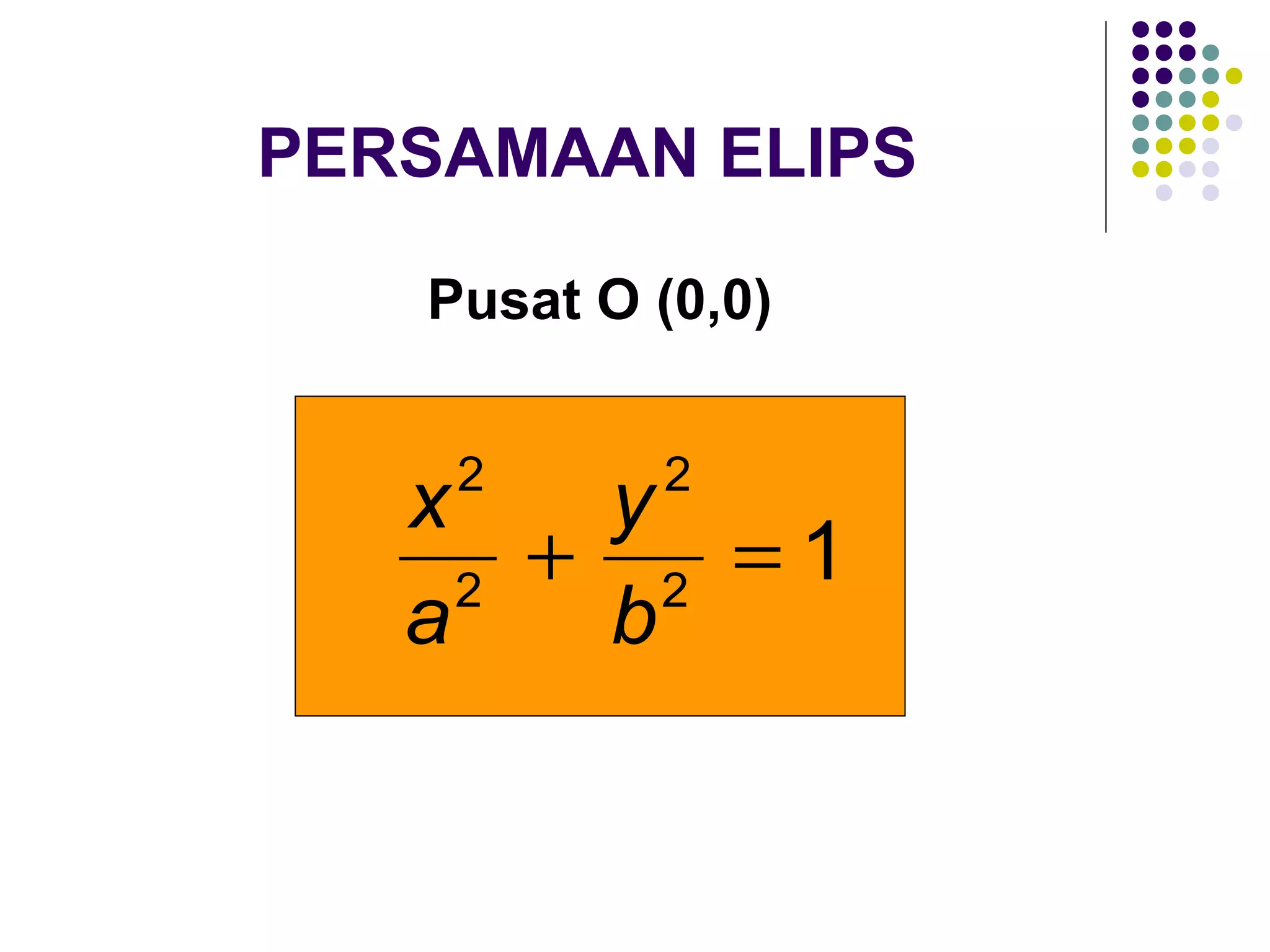
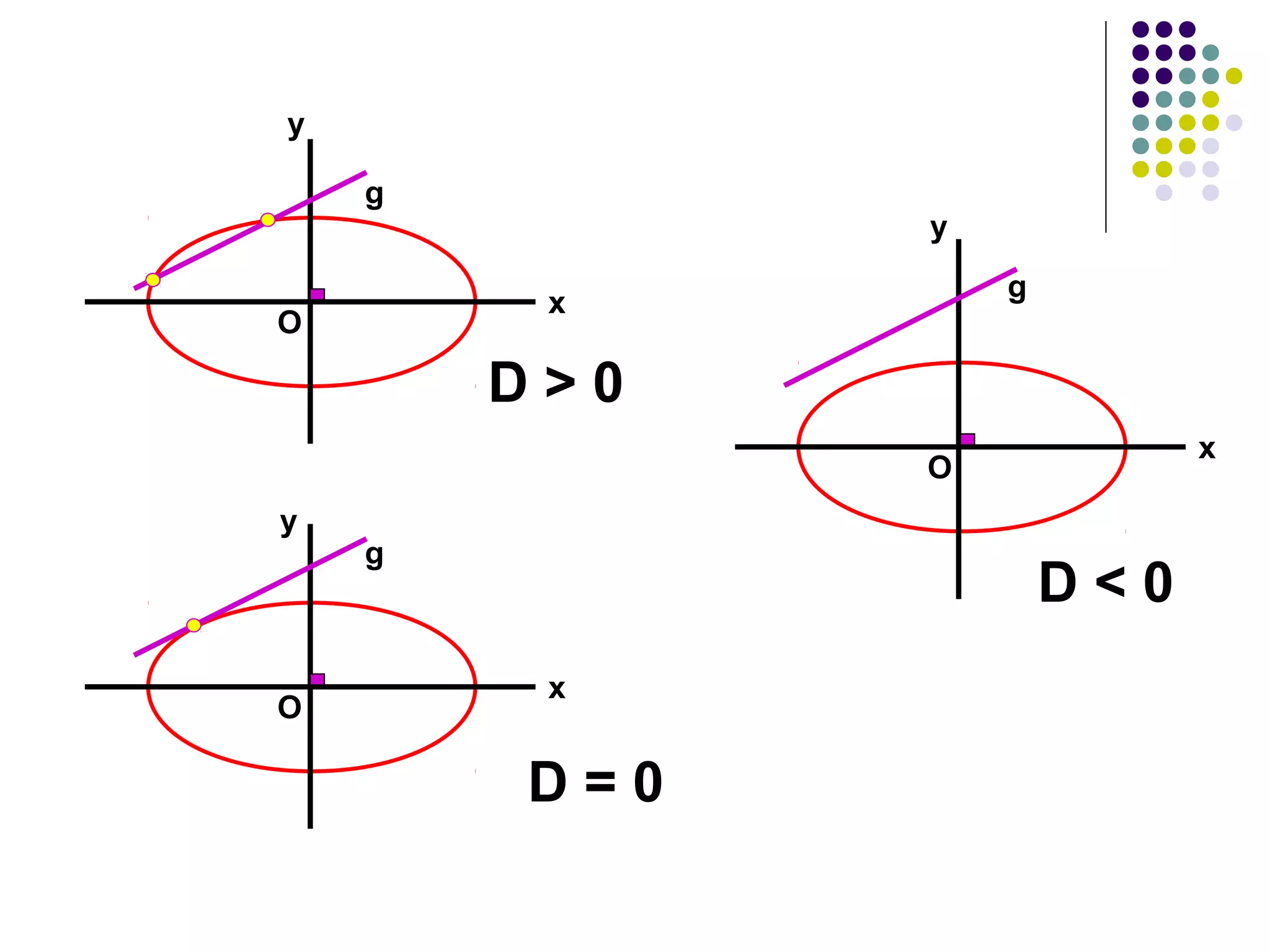
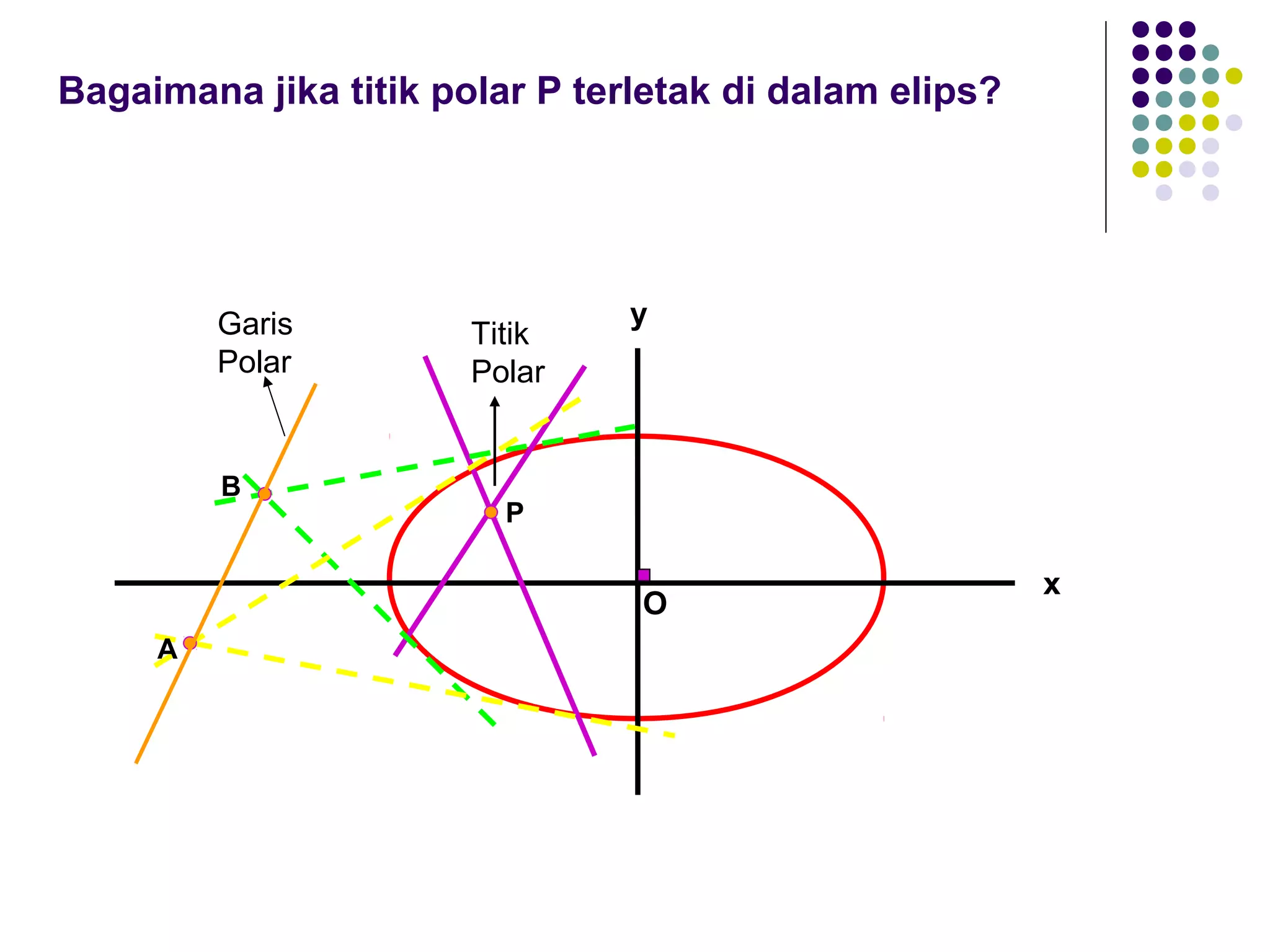
Dokumen ini membahas tentang elips, termasuk definisi, persamaan, sumbu simetri, eksentrisitas, direktris, dan latus rectum. Diberikan juga contoh untuk menentukan persamaan elips berdasarkan pusat dan eksentrisitas serta penjelasan tentang garis singgung dan titik polar. Selain itu, terdapat latihan untuk memperdalam pemahaman tentang konsep yang dijelaskan.

1. ELIPS
Tempat kedudukan titik-titik yang
jumlah jaraknya terhadap dua titik
tertentu mempunyai nilai yang
tetap
Titik tertentu itu dinamakan
fokus atau titik api dari elips

2. F1
F2A1 A2

3. F1(-c,0)A1(-a,0) F2(c,0)O
b
c
a
A2(a, 0)
B1(0, b)
B2(0, -b)
P(x, y)
Misal titik tersebut titik P, maka :
PF1 + PF2 = 2a

4. F1(-c,0)A1(-a,0) F2(c,0)O
b
c
a
A2(a, 0)
B1(0, b)
B2(0, -b)
P(x, y)
Jika titiknya A2, maka :
A2F1 + A2F2 = 2a
(a + c) + (a – c) = 2a
2a = 2a

5. F1(-c,0)A1(-a,0) F2(c,0)O
b
c
a
A2(a, 0)
B1(0, b)
B2(0, -b)
P(x, y)
Jika titiknya B1, maka :
222
22
22
2222
2111
22
2
2
acb
acb
acb
acbcb
aFBFB
=+
=+
=+
=+++
=+

6. PERSAMAAN ELIPS
12
2
2
2
=+
b
y
a
x
Pusat O (0,0)

7. SUMBU SIMETRI
 Sumbu simetri yang melalui titik fokus F1 dan F2
disebut sumbu utama atau sumbu transversal
 Ruas garis A1A2 disebut sumbu panjang atau sumbu
mayor
 Sumbu simetri yang melalui titik tengah F1 dan F2
yang tegak lurus sumbu utama disebut sumbu
sekawan atau sumbu konjugasi
 Ruas garis B1B2 disebut sumbu pendek atau sumbu
minor

8. Menentukan eksentrisitas,
direktris dan lactus rectum
Definisi elips :
Perbandingan kedudukan titik-titik yang
berjarak sama terhadap suatu titik dan suatu
garis tetap harganya antara 0 dan 1

9. F1A1
F2 A2
B1
O
b
B2
c
a
x = -k x = k
Q P

10.  Ambil titik tertentu : A2
)1(....
)(
222
2
22
caaeke
caeak
FAPeA
PA
FA
e
−=−
−=−
=
=
 Ambil titik tertentu : A1
)2(....
)(
211
1
21
cakeae
caeka
FAPeA
PA
FA
e
+=+
+=+
=
=
F1A1
F2 A2
B1
O
b
B2
c
a
x = -k x = k
Q P

11. Subsitusi (1) dan (2)
direktrispers
e
a
k
kea
kea
aekeca
aekeca
.
22
→=
=
=
+=+
−=−

12. Subsitusi (1) dan (2)
taseksentrisi
a
c
e
aec
aec
aekeca
aekeca
→=
=
=
+=+
−=−
22

13. Contoh :
Tentukan persamaan elips dengan
pusat (1,2) dan eksentrisitas 4/5
sedangkan direktrisnya 4x = 25

14. F1A1
L1
L1’
F2 A2
L2(c, -y)
L2’(c, y)
B1
O
b
B2
c
a
Menentukan latus rectum
Definisi:
Garis yang melalui F1 dan F2 tegak
lurus sb. Utama memotong elips di L1 dan L’1
L1L1’ = L2L2’ =
latus rectum

15. a
b
y
a
b
y
bbya
cabya
bcbaya
baaybc
b
y
a
c
b
y
a
x
elipsL
2
2
4
2
2222
22222
222222
222222
2
2
2
2
2
2
2
2
1
)(
1
1
±=→=
=
−=
−=
=+
=+
=+
∈
a
b
a
b
a
b
FLFLLL
maka
a
b
cL
dan
a
b
cL
diperoleh
2
22
212111
2
1
2
1
2
''
,,'
,
:
=
+=
+=






−






Panjang lactus rectum

16. ANALOG DENGAN
PERSAMAAN ELIPS PUSAT
( ) ( ) 12
2
2
2
=
−
+
−
b
y
a
x βα
( )βα,
e
a
hk
a
c
e ±== ,

17. GARIS SINGGUNG
Misal garis )1(.........cmxyg +=≡
)2(...........12
2
2
2
=+
b
y
a
x
)(4
02)(
)(
222222
222222222
222222
cbmabaD
bacamcxaxbma
bacmxaxb
−+=
=−+++
=++
Pers. Elips
maka :

18. g
O
x
y
g
O
x
y
g
O
x
y
D = 0
D > 0
D < 0

19. Persamaan garis singgung
bergradien p
12
1
2
1
=+
b
yy
a
xx

20. TITIK DAN GARIS POLAR
Misal sebuah titik P(x1, Y2) diluar suatu
elips . Dari titik P ditarik dua buah garis
singgung, maka garis hubung p antara
kedua titik singgungnya disebut garis
polarnya P terhadap elips dan P sebagai
titik polar dari garis p tersebut.

21. x
O
y
P (x1, y1)
Q (x2, y2)
R (x3, y3)
Titik Polar
Garis Polar

22. Akan dibuktikan:
12
1
2
1
=+
b
yy
a
xx
merupakan persamaan garis polar
titik P(x1, y1) yang terletak diluar
elips terhadap elips tersebut

23. Bagaimana jika titik polar P terletak di dalam elips?
x
O
y
P
Titik
Polar
Garis
Polar
A
B

24. Latihan (Hal 20 – 23)
 No. 4
 No. 7
 No. 26