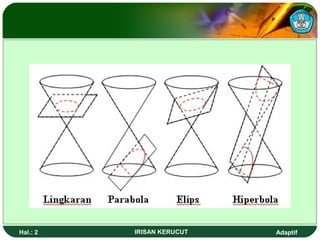
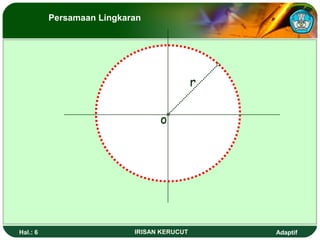
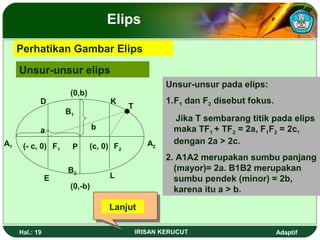
Dokumen ini membahas tentang persamaan lingkaran, elips, dan parabola, termasuk cara menentukan titik pusat, fokus, serta persamaan dari masing-masing bentuk. Terdapat contoh soal dan latihan yang memperlihatkan penerapan konsep-konsep tersebut secara praktis. Selain itu, dokumen ini juga menjelaskan unsur-unsur dan grafik dari elips serta parabola.

1. PERSAMAAN LINGKARAN

2. Hal.: 2 IRISAN KERUCUT Adaptif

3. Hal.: 3 IRISAN KERUCUT Adaptif

4. Persamaan Lingkaran
Hal.: 4 IRISAN KERUCUT Adaptif

5. Persamaan lingkaran
LINGKARAN DIDEFINISIKAN SEBAGAI
HIMPUNAN TITIK TITIK YANG
BERJARAK TETAP TERHADAP TITIK
TERTENTU, DIMANA TITIK TERTENTU
TERSEBUT DISEBUT SEBAGAI PUSAT
LINGKARAN DAN JARAK YANG TETAP
DISEBUT JARI - JARI
Hal.: 5 IRISAN KERUCUT Adaptif

6. o
r
Persamaan Lingkaran
Hal.: 6 IRISAN KERUCUT Adaptif

7. Persamaan Lingkaran
Persamaan Lingkaran
PPeerrssaammaaaann LLiinnggkkaarraann BBeerrppuussaatt ddii TTiittiikk OO((00,,00))
ddaann BBeerrjjaarrii--jjaarrii rr
PPeerrssaammaaaann LLiinnggkkaarraann BBeerrppuussaatt ddii TTiittiikk PP((aa,,bb))
ddaann BBeerrjjaarrii--jjaarrii rr
Hal.: 7 IRISAN KERUCUT Adaptif

8. Y
o
r
T (x,y)
OT = r
( x2 - x1 )2 + ( y2 - y1 ) 2= r
X ( x - 0 ) 2 + ( y - 0 ) 2 = r
x 2 + y 2 = r 2
Hal.: 8 IRISAN KERUCUT Adaptif

9. Persamaan Lingkaran
Hal.: 9 IRISAN KERUCUT Adaptif

10. Persamaan lingkaran
Soal Latihan
Tentukan persamaan lingkaran yang berpusat
di titik O (0,0) dan :
a. berjari-jari 2
b. melalui titik (3,4)
Hal.: 10 IRISAN KERUCUT Adaptif

11. r T (x,y)
P (a,b )
PT = r
( x2 - x1 ) +2 ( y2 - y1 ) =2 r
( x - a ) + ( y - b ) = r 2 2
(x-a) 2 + (y-b) 2= r 2
Y
O X
Hal.: 11 IRISAN KERUCUT Adaptif

12. Persamaan Lingkaran
Hal.: 12 IRISAN KERUCUT Adaptif

13. Persamaan lingkaran
Soal Latihan
Tentukan persamaan lingkaran jika :
a. Berpusat di titik P (3,2) dan berjari-jari 4
b. Berpusat di titik Q (2,-1) dan melalui titik R(5,3)
Hal.: 13 IRISAN KERUCUT Adaptif

14. Hal.: 14 IRISAN KERUCUT Adaptif

15. ELIPS
Hal.: 15 IRISAN KERUCUT Adaptif

16. Elips
Standar Kompetensi
Menerapkan konsep irisan kerucut dalam memecahkan
masalah.
Kompetensi dasar:
3. Menerapkan konsep elips
Indikator
1. Menjelaskan pengertian elips.
2. Menentukan unsur-unsur elips.
3. Menentukan persamaan elips
4. Melukis grafik persamaan ellips
Hal.: 16 IRISAN KERUCUT Adaptif

17. Elips
Indikator
1. Menjelaskan pengertian elips.
2. Menentukan unsur-unsur elips.
3. Menentukan persamaan elips.
4. Melukis grafik persamaan elips.
Hal.: 17 IRISAN KERUCUT Adaptif

18. Elips
Pengertian Elips
Elips adalah tempat kedudukan titik-titik pada
bidang datar yang jumlah jaraknya terhadap dua
titik tertentu yang diketahui adalah tetap (konstan).
Hal.: 18 IRISAN KERUCUT Adaptif

19. Elips
Perhatikan Gambar Elips
Unsur-unsur pada elips:
1.F1 dan F2 disebut fokus.
Jika T sembarang titik pada elips
maka TF1 + TF2 = 2a, F1F2 = 2c,
dengan 2a > 2c.
2. A1A2 merupakan sumbu panjang
(mayor)= 2a. B1B2 merupakan
sumbu pendek (minor) = 2b,
karena itu a > b.
Unsur-unsur elips
b
(0,b)
B1
D
a
·T
A2
(- c, 0) F1 P (c, 0) F2
E
Hal.: 19 IRISAN KERUCUT Adaptif
A1
B2
(0,-b)
K
L
Lanjut

20. Elips
Lanjutan Elips
3. Latus Rectum yaitu segmen garis yang dibatasi elips, tegak lurus
sumbu mayor dan melalui fokus (DE dan KL), panjang Latus Rectum
DE = KL =
2b2
a
4. Titik pusat (P) yaitu titik potong sumbu mayor dengan sumbu minor.
5. Titik puncak elips yaitu titik A1, A2, B1, B2.
Hal.: 20 IRISAN KERUCUT Adaptif

21. Elips
Persamaan Elips
1. Persamaan Elips yang berpusat di O(0,0)
Persamaan Elips : TF1 + TF2 = 2a
(x + c)2 + y2 (x - c)2 + y2
(x + c)2 + y2 (x - c)2 + y2
+ = 2a
= 2a -
Mengkuadratkan ruas kiri dan kanan
sehingga diperoleh ……
·
(0, ) 1 B b
T(x, y)
( ,0) 1 A -a ( ,0) 2 A a
(0, ) 2 B -b
(a2- c2) x2 + a2y2 = a2(a2-c2) . . . (i), jika titik T pada titik puncak pada
sumbu minor (0,b) maka diperoleh … . b2 =a2 – c2 . . . . (ii)
Persamaan (ii) disubstitusikan ke persamaan (i) sehingga diperoleh:
2
2
+ =
1 2
2
y
b
x
a
Hal.: 21 IRISAN KERUCUT Adaptif

22. Elips
Contoh
Tentukan persamaan elips dengan titik puncak (13,0) dan fokus
F1(-12, 0) dan F2(12,0).
Jawab:
Diketahui pusat elips O(0,0)
Titik puncak (13,0) Þ
a = 13
Titik fokus (-12,0) dan (12,0) c = 12
Þ
Sumbu utama adalah sumbu X, sehingga persamaannya:
2
x +y = atau x +y =
1
2 2
169 25
1
2
13 5
2
2
Hal.: 22 IRISAN KERUCUT Adaptif

23. Elips
a. Persamaan elips dengan
titik pusat (m, n):
2
2.Persamaan elips yang bertitik pusat P (m,n)
2
·
y n
x m
- + - =
( ) ( ) 1
2
2
b
a
Y
O
B
X= m
P(m,n)
· ·
A F1 F2
C
D
X
m
3.Titik fokus F1(m-c, n) dan F2( m + c, n )
·
4. Titik puncak A(m-a, n) dan B ( m + a, n )
5. Panjang lactus rectum (LR) = dengan b2 = a2 -c2
b. Sumbu utamanya (sumbu) y = n,
dengan panjang 2a dan sumbu
minornya adalah sumbu x = n,
dengan panjang 2b.
2b2
a
Hal.: 23 IRISAN KERUCUT Adaptif

24. Elips
Contoh:
Tentukan persamaan elips dengan fokus F1(1,3) dan F2(7,3) dan
puncaknya (10,3).
Jawab:
Þ
Fokus (1,3) dan (7,3) = m-c = 1, m + c = 7 dengan eliminasi
Þ
diperoleh m=4 dan c= 3
Pusat P (m,n) = P (4,3) m = 4
Puncak(10,3) m + a= 10 a= 6
b2 = a2 –c2 = 62 - 32 = 36 - 9 = 27
Sumbu utama y=3, sehingga persamaan elips menjadi:
Þ
Þ
Þ
1
( 4) 2 2 2
x - + y - = atau x - + ( y - 3)
=
27
1 ( 4)
36
( 3)
27
6
2
2
Hal.: 24 IRISAN KERUCUT Adaptif

25. Elips
Bentuk umum persamaan elips
Persamaan elips memiliki bentuk umum:
Ax2 + By2 +Cx + Dy + E = 0
Ax2 + By2 + Cx + Dy + E = 0
Hubungan antara persamaan dengan
persamaan x m
2
y n
2
adalah sebagai berikut:
- + - =
( ) ( ) 1
Ax2 + By2 +Cx + Dy + E = 0
2
2
b
a
Jika A > B, maka A = a2, B = b2, C=-2a2m, D= -2b2n, E= a2m2 + b2n2- a2b2
Jika A < B, maka A = b2, B = a2, C=-2b2m, D= -2a2n, E= a2m2 + b2n2- a2b2
Hal.: 25 IRISAN KERUCUT Adaptif

26. Elips
Contoh:
Tentukan titik pusat dan fokus dari elips yang memiliki
persamaan 4x2+ 9y2 -16x+ 18y -11=0.
Jawab:
Diketahui persamaan elips: 4x2+ 9y2 -16x+ 18y -11=0.
A=4, B= 9, C= -16, D=18, E= -11
b2 = A = 4 b Û
= 2
A2 = B = 9 Û a = 3
C = -2 b2m D= -2a2m C2= a2 –b2 = 9 -4 = 5
-16=-2. 4. m 18= -2. 9.n C =
-16= -8m 18= -18n
2= m -1 = n
Pusat P(m,n) Û
P(2, -1)
FokusF2(m-c, n)=F2 dan F2(m+c, n)=F2
(2 - 5, -1) (2 + 5, - 1)
Hal.: 26 IRISAN KERUCUT Adaptif

27. Elips
Persamaan garis singgung melalui titik (x1, y1) pada elips
2
+ y
2
=
x
1. Untuk persamaan elips persamaan garis
1 2
2
b
a
singgung yang melalui (x1, y1) pada elips tersebut adalah:
x x 1 2
atau
y y
1 + 1
=
b
a
2
b2x x +a y y = a b
2 2
1
2
1
2
2
y n
x m
- + - =
( ) ( ) 1
2. Untuk persamaan elips persamaan garis
2
2
b
a
singgung yang melalui (x1, y1) pada elips tersebut adalah:
x -m x -m + - -
y n y n
1 ( )( ) ( )( )
2
1
2
b
a
Hal.: 27 IRISAN KERUCUT Adaptif

28. Elips
Persamaan garis singgung dengan gradien p
2
2
+ =
Pada elips x atau b 2 x 2 + a 2 y 2 = a 2 b 2 ,adalah
1 2
2
y
b
a
y= p x ± a2 p2 +b2
Untuk elips dengan persamaan:
2
2
y n
x m
- + - =
( ) ( ) 1
2
a
Persamaan garis singgungnya adalah:
y - n = p(x-m)
2
b
± a2 p2 +b2
Hal.: 28 IRISAN KERUCUT Adaptif

29. Elips
Contoh:
Tentukan persamaan garis singgung elips berikut.
1,
2 2
x + y =
a. pada titik (4, 3)
28 21
1,
( x - 1)2 2
+ ( y + 2)
=
b. pada titik(5,-3)
18
Jawab:
9
a. Diketahui :
1,
2 2
x + y =
28 21
Û
(4,3) x1 = 4 dan y1= 3
Persamaan garis singgung:
y y
x x
1 + =
1 2
1
2
b
a
Hal.: 29 IRISAN KERUCUT Adaptif

30. Elips
Û4x + y =
1
3
21
28
Ûx + y =
Ûx + y = 7
1
7 7
(x 1)2 y 2
- + ( + 2)
= 1Þ
b. Diketahui: pusat (m, n) = (1, -2)
9
18
Þx1=5dan
( 5, -3) y1 = -3
Persamaan garis singgung:
y n y n
x m x m
1 - - + - - =
( )( ) ( )( ) 1
2
1
2
b
a
Hal.: 30 IRISAN KERUCUT Adaptif

31. Elips
1
Û(5-1)(x -1) + ( - 3 + 2)
=
9
18
Û4(x -1) +- y + =
1
( 2)
9
18
1
Û2(x -1) + - ( y + 2)
=
9
9
Û 2(x - 1) - (y - 2) = 9
Û2x - y =13
Hal.: 31 IRISAN KERUCUT Adaptif

32. Hal.: 32 IRISAN KERUCUT Adaptif

33. Parabola
Persamaan parabola berpuncak 0(0,0)
y2 = 4px
a.Puncak (0,0)
b. Sumbu semetri = sumbu x
c. Fokusnya F(p,0)
d. Direktriknya x = -p
Y
• • •
(0,0) X
d:X=-P
F(P,0)
Hal.: 33 IRISAN KERUCUT Adaptif

34. Parabola
Persamaan parabola yang bepuncak 0(0,0) dan Fokus di
F(-p,0) adalah
Y2 = -4px
X
Y
• •
F(-P,0)(0,0)
d:X=P
•
•
Hal.: 34 IRISAN KERUCUT Adaptif

35. Parabola
Persamaan parabola yang bepuncak 0(0,0) dan Fokus di
F(0,p) adalah
x2 = 4py
X
Y
F(0,p)
•
•
(0,0)
•
d:y=-P
Hal.: 35 IRISAN KERUCUT Adaptif

36. Parabola
Persamaan parabola yang bepuncak 0(0,0) dan Fokus di
F(0,-p) adalah
x2 = -4py
d: y=p
X
Y
•
•
(0,0)
•
F(0,-p)
Hal.: 36 IRISAN KERUCUT Adaptif

37. Parabola
Contoh:
1.Dari parabola-parabola berikut tentukan koordinat
fokus,persamaan sumbu semetri,persamaan direktris dan
panjang lactus rectum
a. y2 = 4x c. x2 = -8y
b. y2 = -12x d. x2 = 6y
Jawab:
a. y2 =4px y2 = 4x, maka p = 1
Parabola ini merupakan parabola horizsontal ysng
terbuka ke kanan.
(i) Koordinat titik fokus F(p,0) F(1,0)
(ii) Sumbu semetri berimpit dengan sumbu X, maka
persamaanya y = 0
(iii) Persamaan direktris: x = -p x = -1
(iv) Panjang lactus rectum (LR) = 4p = 4 . 1 = 4
Hal.: 37 IRISAN KERUCUT Adaptif

38. Parabola
b. y2 =-p4x y2 = -12x, maka 4p = 12 p = 3
Parabola ini merupakan parabola horizsontal yang
terbuka ke kiri
(i) Koordinat titik fokus F(-p,0) F(-3,0)
(ii) Sumbu semetri berimpit dengan sumbu X, maka
persamaanya y = 0
(iii) Persamaan direktris: x = -p x = 3
(iv) Panjang lactus rectum (LR) = 4p = 4 . 3= 12
c. x2 = -p4y x2 = -8y, maka 4p = 8 p = 2
Parabola ini merupakan parabola horizsontal ysng terbuka ke bawah
(i) Koordinat titik fokus F(0,-p) F(0,-2)
(ii) Sumbu semetri berimpit dengan sumbu y, maka
persamaanya x = 0
(iii) Persamaan direktris: y = p y = 2
(iv) Panjang lactus rectum (LR) = 4p = 4 . 2 = 8
d. Untuk latihan
Hal.: 38 IRISAN KERUCUT Adaptif

39. Parabola
Persamaan parabola berpuncak P(a,b)
(y – b)2 = 4p(x – a)
•
•
Fp(a+p,b)
• •
y
P(a,b)
a
• x
O(0,0) F(•p,0)
•
•
•
a. Titik puncak P(a,b)
b. Titik fokus F(a+p,b)
c. Direktris x = -p+a
d. Sumbu semetri y = b
e.
Hal.: 39 IRISAN KERUCUT Adaptif

40. Parabola
Contoh:
Diberikan persamaan parabola 3x – y2 + 4y + 8= 0
Tentukan : a. Titik puncak c. Direktris
b. Titik fokus d. Sumbu semetri
Jawab:
Ubah persamaan parabola ke persamaan umum:
3x – y2 + 4y + 8= 0
y2 - 4y = 3x + 8
y2 - 4y + 4 = 3x + 8 + 4
(y – 2)2 = 3x + 12
(y – 2)2 = 3(x + 4)
Didapat persamaan parabola (y – 2)2 = 3(x + 4) yaitu
parabola mendatar yang terbuka ke kanan.
Hal.: 40 IRISAN KERUCUT Adaptif

41. Parabola
Dari persamaan tersebut diperoleh:
a. Titik puncak P(-4,2)
b. 4p = 3 maka p =
3
4
Titik Fokus F(a+p,b)
F(-4 + 3
,2)
4
F(-3 1
,2)
4
c. Persamaan direktris :
x p a
= - + = - -
x
= -
d. Sumbu semetrinya : y = 2
4 3
4
F
P(-4,2)
4
3
4
y
O(0,0) x
Hal.: 41 IRISAN KERUCUT Adaptif

42. Parabola
Soal untuk latihan:
a.Tentukan persaaman parabola yang
berpuncak di (2,4) dan fokusnys (-3,4)
b.Tentukan persamaan Parabola yang titik
fokusnya F(2-3) dan persamaan didertrisnya
y = 5
Hal.: 42 IRISAN KERUCUT Adaptif

43. Persamaan garis singgung parabola
A. Persamaan garis singgung parabola melaluhi titik A(x1,y1)
yy1 = 2p(x+x1)
x
y
•
A•(x1,y1)
Hal.: 43 IRISAN KERUCUT Adaptif

44. Persamaan garis singgung parabola
Persamaan parabola melaluhi titik A(x1,y1) di sajikan pada
tabel berikut
Persamaan Parabola Persamaan Garis singgung
y2 = 4px yy1 = 2p(x+x1)
y2 = -4px yy1 = -2p(x+x1)
x2 = 4py xx1 = 2p(y+y1)
x2 = -4py xx1 = -2p(y+y1)
(y – b)2 = 4p(x – a) (y-b)(y1-b)=2p(x+x1-2a)
(y – b)2 = -4p(x – a) (y-b)(y1-b)=-2p(x+x1-2a)
(x– a)2 = 4p(y – b) (x-a)(x1-a)=2p(y+y1-2b)
(x– a)2 = -4p(y – b) (x-a)(x1-a)=-2p(y+y1-2b)
Hal.: 44 IRISAN KERUCUT Adaptif

45. Persamaan garis singgung parabola
Contoh:
1. Tentukan persamaan garis singgung parabola y2 = 8x di
titik (2,4)
jawab :
y2 = 8x
4p = 8
p = 2
Titik A(x1,y1) A(2,4)
Persamaan garis singgungnya adalah
yy1 = 2p(x+x1)
y.4 = 2.2(x+2)
4y = 4(x+2)
y = x+2
Hal.: 45 IRISAN KERUCUT Adaptif

46. Persamaan garis singgung parabola
2. Tentukan persamaan garis singgung parabola
(x+1)2 = -3(y-2) pada titik (2,-1)
Jawab :
a = -1 , b = 2, x1 = 2 dan y1 = 1
(x+1)2 = -3(y-2)
-4p = -3
p =
3
4
Persamaan garis singgung parabola di titik A(2,-1) adalah
(x - a)(x1 - a) = -2p(y + y1 - 2b)
(x +1)(2 +1) = -2. 3
4
(y - 1 – 2.2)
(x + 1)(3) =
- 3 ( y -
5)
2
6(x + 1) = - 3(y – 5)
2(x + 1) = -(y – 5)
2x + 2 = -y + 5
y = -2x + 3
Hal.: 46 IRISAN KERUCUT Adaptif

47. Persamaan garis singgung parabola
B.Persamaan garis singgung parabola yang bergradien m
Persamaan parabola Persamaan garis singgung
p
y2 = 4px y = mx +
m
y = mx -
p
y2 =- 4px m
x2 = 4py y = mx – m2p
x2 = -4py y = mx + m2p
p
(y – b)2 = 4p(x – a) (y – b) = m(x – a) +
m
(y – b)2 = -4p(x – a) (y – b) = m(x – a) -
p
m
(x– a)2 = 4p(y – b) (y – b) = m(x – a) – m2p
(x– a)2 = -4p(y – b) (y – b) = m(x – a) + m2p
Hal.: 47 IRISAN KERUCUT Adaptif

48. Persamaan garis singgung parabola
Contoh:
1.Tentukan persamaan garis singgung parabola y2 = 8x yang
kergradien 2
Jawab:
Parabola y2 = 8x
4p = 8
p = 2
Maka persamaan garis singgungnya adalah:
p
y = mx +
y = 2x + 1
m
Hal.: 48 IRISAN KERUCUT Adaptif

49. Persamaan garis singgung parabola
2. Tentukan persamaan garis singgung parabola
(y + 5)2 = -8(x – 2) yang bergradien 3
Jawab :
Parabola (y + 5)2 = -8(x – 2)
-4x = -8
p = 2
Puncak P(2,-5)
Jadi persamaan garis singgungnya adalah
y – b = m(x – a) –
y + 5 = 3(x – 2) –
2
3
3y + 15 = 9(x – 2) -2
3y + 15 = 9x – 20
9x – 3y + 35 = 0
y = 3x -
p
m
35
3
Hal.: 49 IRISAN KERUCUT Adaptif

50. Hiperbola
A.Hiperbola adalah kedudukan titik-titik pada bidang datar yang
selisih jaraknya terhadap dua titik tertentu adalah tetap.
Kedua titik tertentu di sebut fokus(titik apai).
b
x a
x
y
Y =
M K
D
• • 0• • •
F’(-C,0) F(C,0)
E L
Y =
A B
- b
x
a
A.Persamaan Hiperbola Pusat(0,0)
N
2
2
- =
x
y
1 a
2
b
2
a. Pusat O(0,0)
b. Fokus F’(-C,0) dan F(C,0)
c. Puncak A(-a,0) dan B(a,0)
d. Sumbu semetri
- Sumbu Utama sumbu x
- Sumbu sekawan adalah sumbu y
e. Sumbu nyata AB = 2a
f. Sumbu imajiner MN = 2b
b
g. Asimtot , y = + x
a
Hal.: 50 IRISAN KERUCUT Adaptif

51. Hiperbola
b
x a
x
B. Persamaan Hiperbola
y
F(0,C)
•
•
K
B Y =
•
0
A
•
D
E L
•
Y =
- b
y
a
x
a
F’(0,-C)
N
2
2
- =
1 2
2
x
b
atau b2y2 – a2x2 = a2b2
a. Pusat O(0,0)
b. Fokus F’(0,-C) dan F(0,C)
c. Puncak A(0,-a) dan B(0,a)
d. Sumbu semetri
- Sumbu Utama sumbu y
- Sumbu sekawan adalah sumbu x
e. Sumbu nyata AB = 2a
f. Sumbu imajiner MN = 2b
M
b
g. Asimtot , y = + x
a
Hal.: 51 IRISAN KERUCUT Adaptif

52. Hiperbola
Contoh :
1.Tentukan persamaan hiperbola jika titik fokusnya F’(-13,0)
dan F(13,0) dengan puncak (-5,0) dan (5,0)
Jawab :
Pusat (0,0)
a = 5 , c = 13
b2 = c2 – a2
= 132 – 52
= 169 – 25
= 144
Sumbu utama sumbu X, maka persamaan hiperbolanya
adalah:
1
2
x 2 y 2
- = Þ- =
25 144
1
2
2
2
y
b
x
a
Hal.: 52 IRISAN KERUCUT Adaptif

53. Hiperbola
2.Diketahui persamaan hiperbola dari
Jawab :
x 2 + y 2
= 1 Þ a 2
= 16 Û a = 4
dan
b2 = 4Û b = 2
16 4
Pusat(0,0)
Puncak(-a,0)=(-4,0) dan (a,0) = (4,0)
1
2 2
x + y =
16 4
c2 = a2 + b2 = 16 + 4 = 20 Û c = 20 = 2 2
Fokus(-c,0) = (-2 5,0)dan(C,0) = (2 2,0)
Persamaana sin tot : y = ± b
x a
= 2 dan
y x
3
y = - 2
4
Hal.: 53 IRISAN KERUCUT Adaptif

54. Hiperbola
A. Persamaaan Hiperbola dengan pusat P(m,n)
b
x a
x
2
2
y n
x m
- - - =
( ) ( ) 1
y
Y =
2
b
M K
D
• • • • •
F’(-C,0) F(C,0)
0
P
E L
Y =
A B
- b
x
a
N
2
a
a. Pusat P(m,n)
b. Fokus F’(m-C,0) dan F(m+C,0)
c. Puncak A(m-a,0) dan B(m+a,0)
d. Sumbu semetri
- S umbu Utama sumbu y = n
- Sumbu sekawan adalah y = m
e. Sumbu nyata AB = 2a
f. Sumbu imajiner MN = 2b
b
g. Asimtot , y-n = + x (x - a)
a
Hal.: 54 IRISAN KERUCUT Adaptif

55. Hiperbola
Contoh:
1. Tentukan persamaan hiperbola jika titik fokus F’(-2,-3) dan F(8,-3) dan
titik puncaknya (7,-3)
Jawab:
fokus F’(-2,-3) dan F(8,-3)
Jarak pusat ke fokus c = 8 – 3 = 5
Puncak (7,3)
Jarak pusat dengan puncak a = 7 – 3 = 4
b2 = c2 – a2 = 52 – 42 = 25 – 16 = 9
Jadi persamaan hiperbola adalah
atau
1
3 2 2
æ x - y
- æ çè÷ø
+ 3
ö 9
ö 16
çè
= ÷ø
9(x-3)2 – 16(y+3)2 = 144
9x2 – 16y2 – 54x -96y – 207 = 0
Þ pusatæ - + - + -
2 8 = - ÷ø
(3, 3)
, 3 ( 3)
ö 2
çè
2
Hal.: 55 IRISAN KERUCUT Adaptif

56. Hiperbola
2. Tentukan titik pusat,titik fokus, titik puncak, panjang lactus rectum dan
persamaan asimtotnya dari
Jawab:
( x - 4 ) 2 ( y + ) 2
- =
1
64
( x - 4 ) 2 ( - y + 1
) 2
=
1
225
64
Titik pusat (4,-1)
1
225
PanjangLactus
rectum b
a2 = 64Ûa =8
b2 = 225Ûb =15
c2 = a2 + b2 = 64 + 225 = 289Û c = 17
Fokus(4 -17,-1) = (-13,-1)dan(4 +17,-1) = (21,-1)
225
4
2 2 2.225
= = =
8
a
Asimtot : y + 1 = ± 15 x -
( 4)
8
Hal.: 56 IRISAN KERUCUT Adaptif

57. Persamaan Garis Singgung Hiperbola
Persamaan garis singgung hiperbola melelaluiT(x1,y1)
Persamaan garis singgung
di titik T(x1,y1) yaitu
di titik T(x1,y1) yaitu
y y
x x
1 - =
1 2
1
2
b
a
2
2
- =
1 2
2
y
b
x
2
x
a
y
Þ - =
1 2
2
2
y n
Þ
2
2
a
x m
b
Þ - - - =
( ) ( ) 1
2
2
b
a
x x
y y
1 - =
1 2
1
2
b
a
y n y n
x x x m
1 - - - - - =
di titik T(x1,y1) yaitu ( )( ) ( )( ) 1
2
1
2
b
a
x m x m
di titik T(x y n y n 1,y1) yaitu
1 - - - - - =
y n 2
x m
2
( )( ) ( )( ) 1
Þ - - - =
( ) ( ) 1
2
2
b
a
2
1
2
b
a
Hal.: 57 IRISAN KERUCUT Adaptif

58. PERSAMAN GARIS SINGGUNG HIPERBOLA
Contoh 1 :
Tentukan persamaan garis singgung pada hiperbola
pada titik (9, -4)
1
2 2
x - y =
9 2
Jawab
Persamaan garis singgung Hiperbola
2
2
- =
1 2
2
y
b
x
a
y y
x x
di titik T(x1,y1) yaitu 1 - 1
=
1 2
2
b
a
9x - - 4
y =
Jadi persamaan garis singgungnya : 1
2
9
atau x + 2y = 1
Hal.: 58 IRISAN KERUCUT Adaptif

59. Persamaan garis singgung Hiperbola
Contoh 2
( x - 2)2 Tentukan persamaan garis singgung hiperbola - ( y + 3)
2
=
1
12
36
Pada titik (-4, -3)
Jawab :
( x - m
) 2
( y - n
)
2
Persamaan garis singgung hiperbola - =
1 2
2
b
a
di titik T(x1,y1) yaitu
1
y n y n
x x x m
1 - - - - - =
( )( ) ( )( ) 1
2
1
2
b
a
Jadi persamaan garissinggungnya : (-4 - 2)(x - 2) - ( - 3 + 3)( y + 3)
=
12
36
Þ-(x -2) - =
Þ-x + 2 = 6
0 1
6
x = - 4
Hal.: 59 IRISAN KERUCUT Adaptif

60. Hal.: 60 IRISAN KERUCUT Adaptif