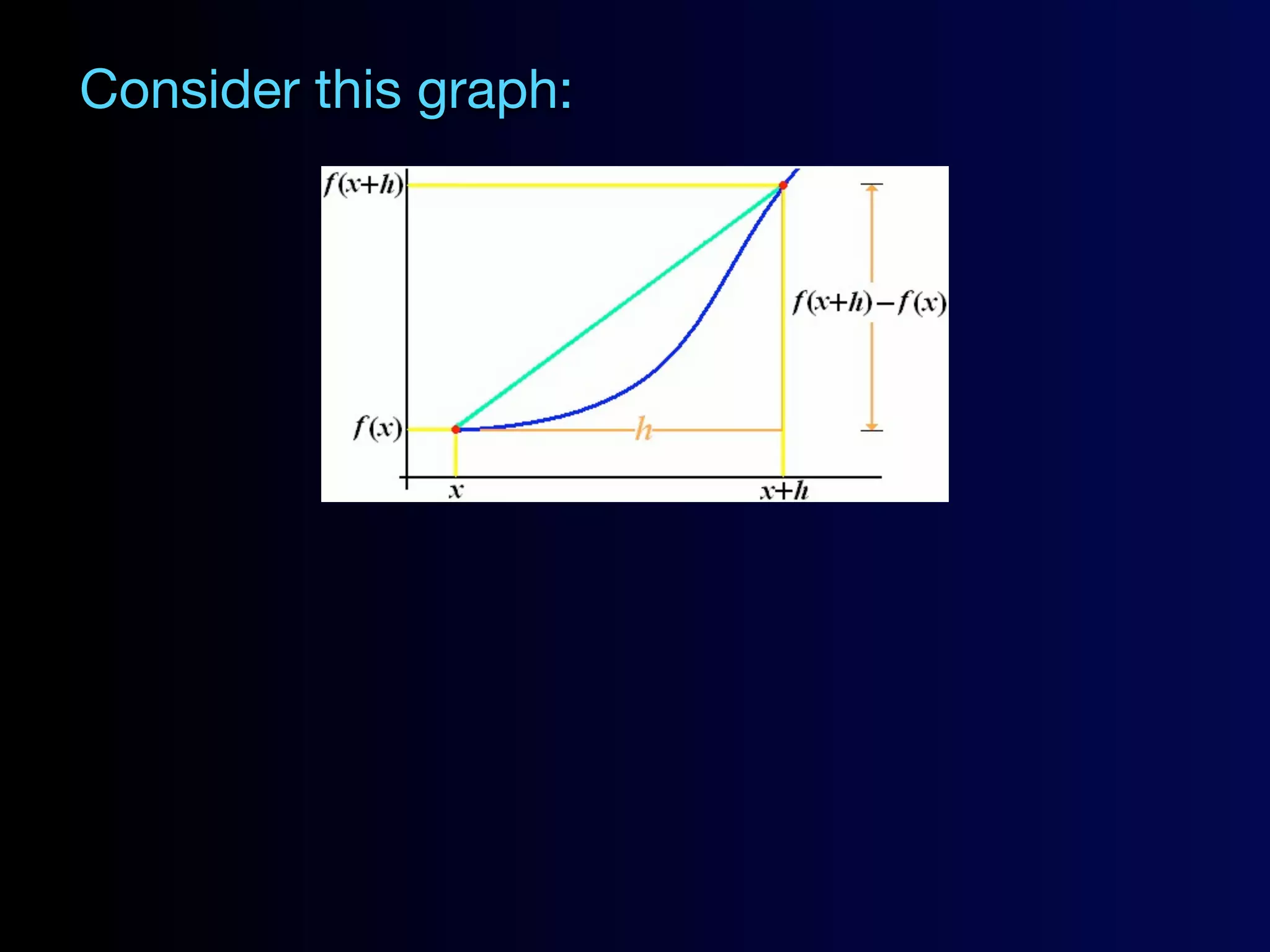
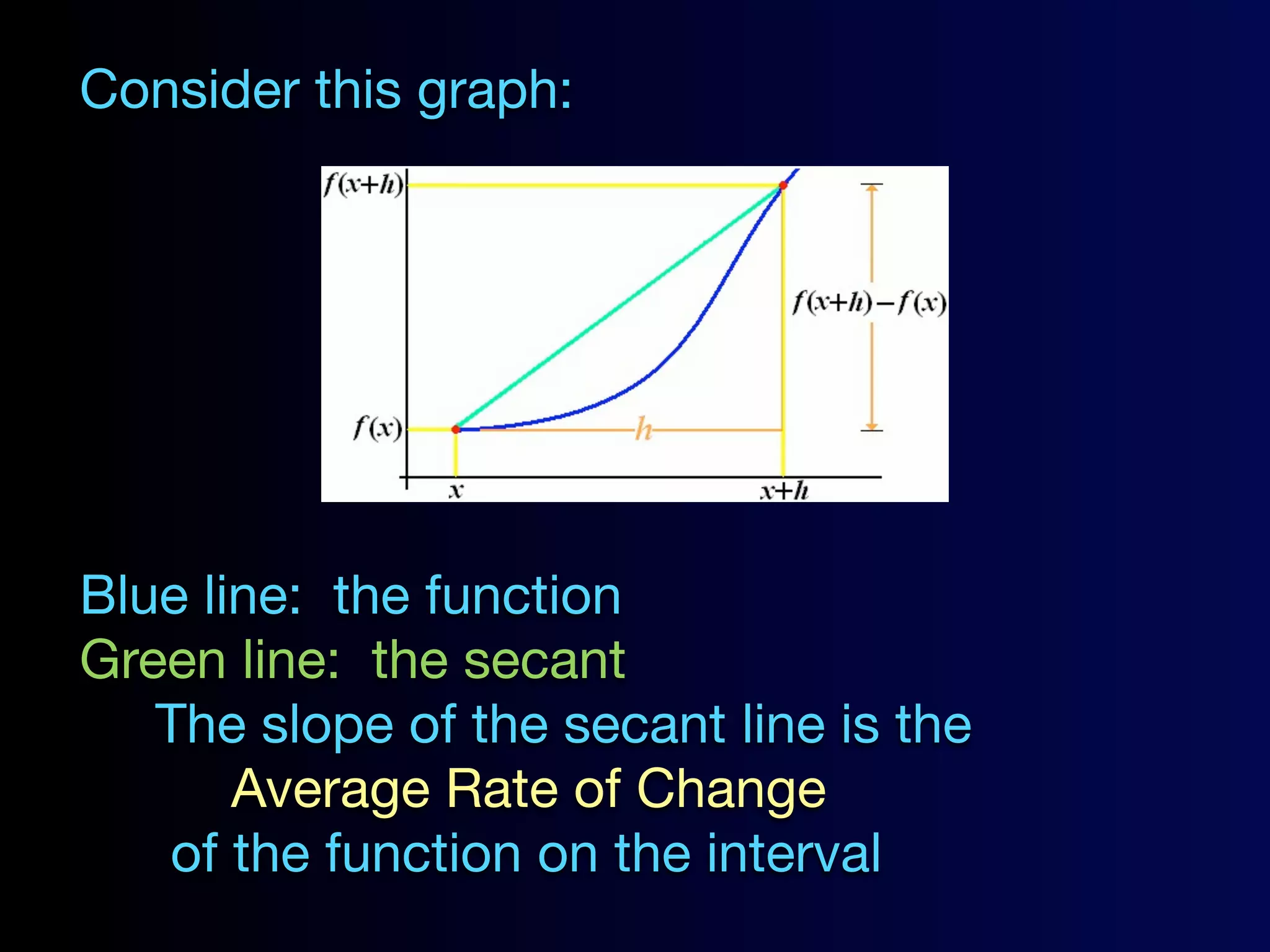
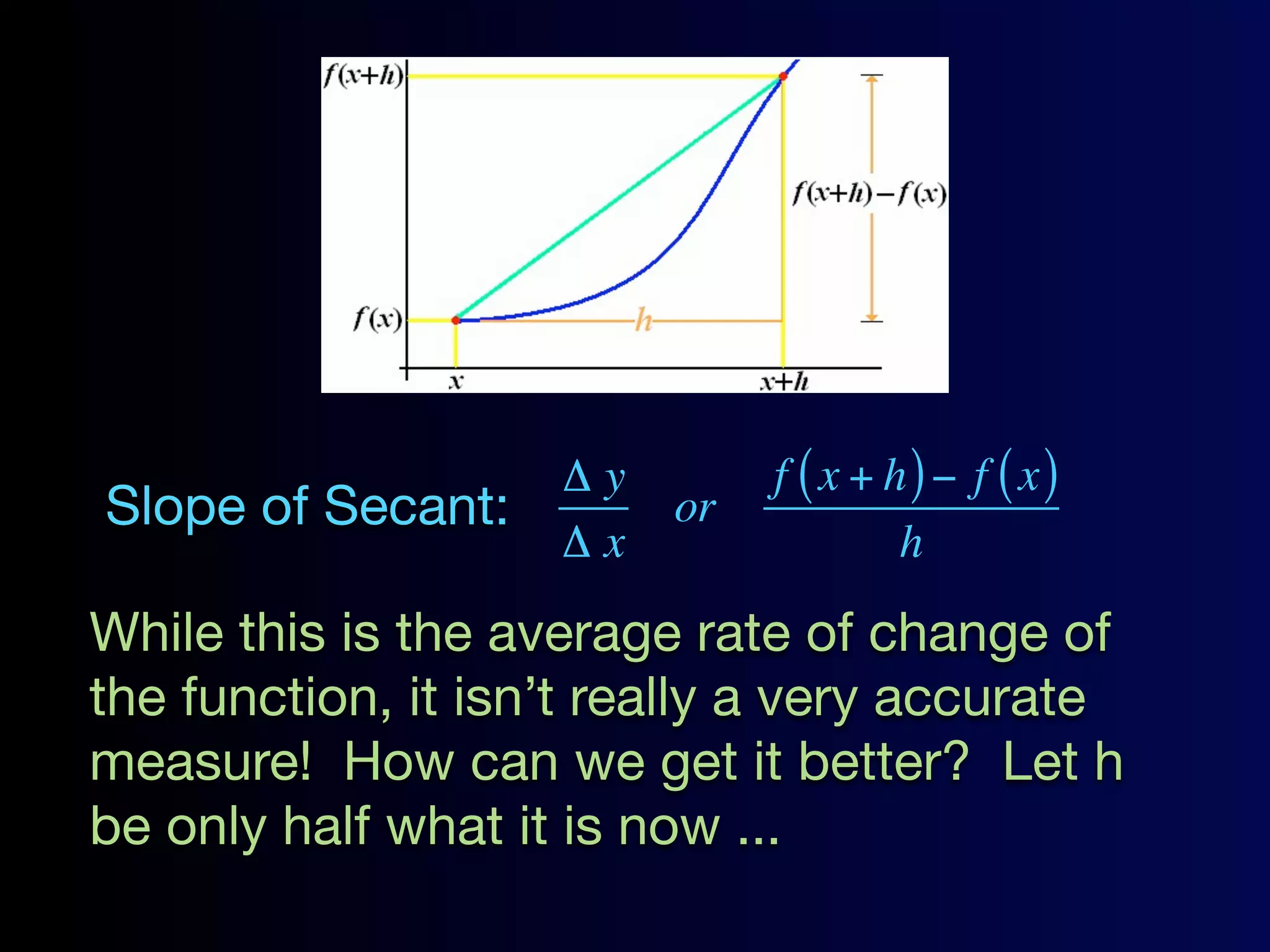
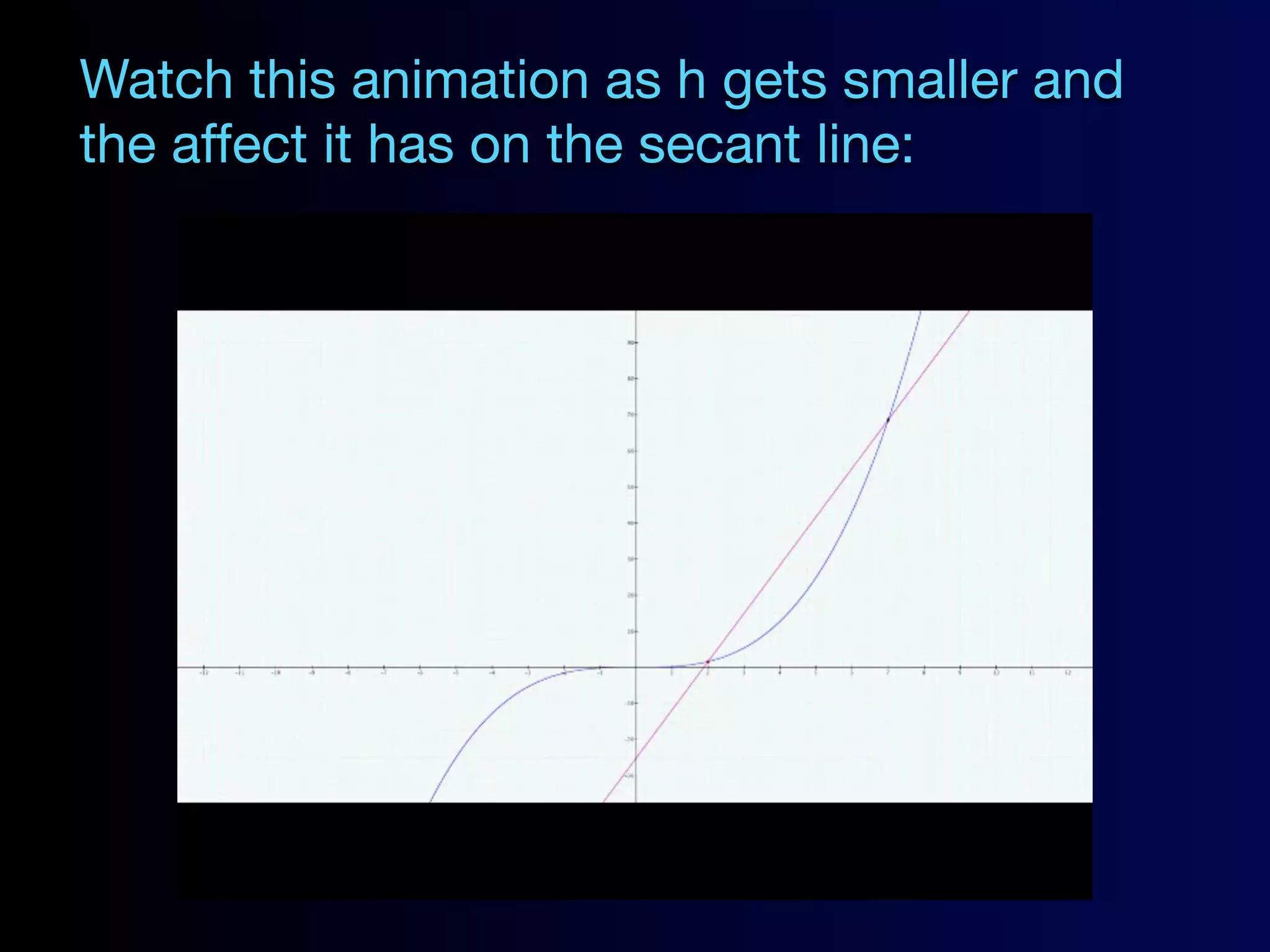
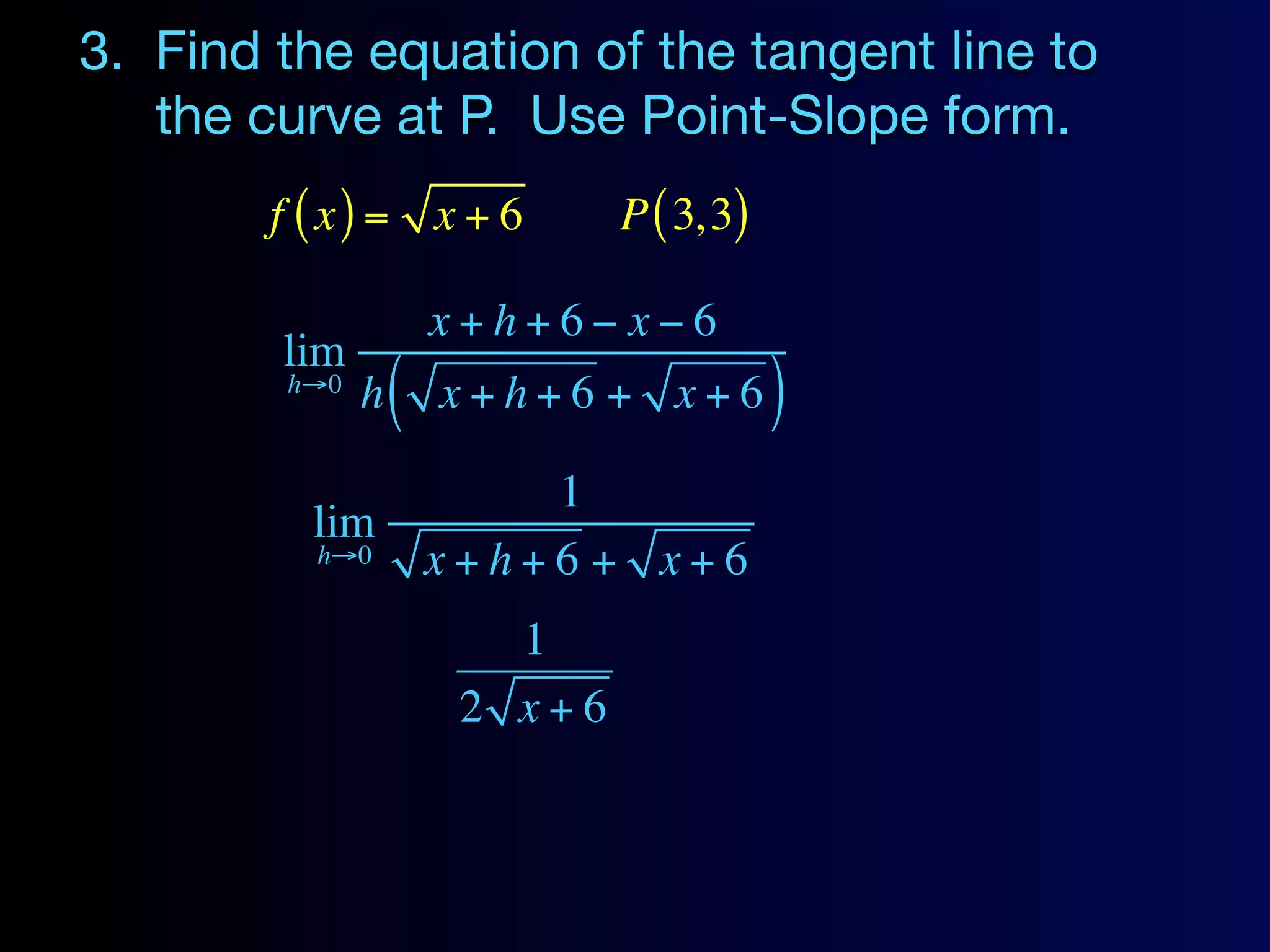Here are the problems from the slides with their solutions: 1. Find the slope of the line tangent to the graph of the function f(x) = x^2 - 5x + 8 at the point P(1,4). Slope = -3 2. Find the equation of the tangent line to the curve f(x) = 2x^2 - 3 at the point P(1,-1) using point-slope form. y - (-1) = 4(x - 1) 3. Find the equation of the tangent line to the curve f(x) = x + 6 at the point P(3,3) using point-slope form. y

1. 12.3 Tangent To A Curve
Revelation 21:4 "He will wipe every tear from their eyes. There
will be no more death, or mourning or crying or pain, for the old
order of things has passed away."

2. Consider this graph:

3. Consider this graph:
Blue line: the function
Green line: the secant
The slope of the secant line is the
Average Rate of Change
of the function on the interval

4. Δy f ( x + h) − f ( x)
Slope of Secant: or
Δx h
While this is the average rate of change of
the function, it isn’t really a very accurate
measure! How can we get it better? Let h
be only half what it is now ...

5. Watch this animation as h gets smaller and
the affect it has on the secant line:

6. Watch this animation as h gets smaller and
the affect it has on the secant line:

7. What will be best is if we allow h to approach
zero as a limit. This then gives us the
Instantaneous Rate of Change of the function
at that specific point!
f ( x + h) − f ( x)
lim
h→0 h

8. What will be best is if we allow h to approach
zero as a limit. This then gives us the
Instantaneous Rate of Change of the function
at that specific point!
f ( x + h) − f ( x)
lim
h→0 h
Since the secant line becomes the tangent
line to the function at that point, this limit is
the slope of that tangent line ... and we call
this value the derivative of the function at that
point. And ... it is the instantaneous rate of
change of that function at that point.

9. I’m going to do some problems on the board,
but I’ll also have the solutions in these slides
so you can review them at a later date.

10. 1. Find the slope of the line tangent to the
graph of the function at P.
2
f ( x ) = x − 5x + 8 P (1, 4 )
end slide

11. 1. Find the slope of the line tangent to the
graph of the function at P.
2
f ( x ) = x − 5x + 8 P (1, 4 )
2. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
2
f ( x ) = 2x − 3 P (1,−1)
end slide

12. 1. Find the slope of the line tangent to the
graph of the function at P.
2
f ( x ) = x − 5x + 8 P (1, 4 )
2. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
2
f ( x ) = 2x − 3 P (1,−1)
3. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
f ( x) = x + 6 P ( 3, 3)
end slide

13. 1. Find the slope of the line tangent to the
graph of the function at P.
2
f ( x ) = x − 5x + 8 P (1, 4 )
f ( x + h) − f ( x)
lim
h→0 h
2
( x + h) − 5 ( x + h ) + 8 − ( x − 5x + 8 )
2
lim
h→0 h
2 2 2
x + 2xh + h − 5x − 5h + 8 − x + 5x − 8
lim
h→0 h
2
2xh + h − 5h
lim
h→0 h

14. 1. Find the slope of the line tangent to the
graph of the function at P. (continued)
2
f ( x ) = x − 5x + 8 P (1, 4 )
2
2xh + h − 5h
lim
h→0 h
h ( 2x + h − 5 )
lim
h→0 h
lim ( 2x + h − 5 )
h→0
2x − 5
at (1, 4 ) : 2 (1) − 5
−3

15. 2. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
2
f ( x ) = 2x − 3 P (1,−1)
f ( x + h) − f ( x)
lim
h→0 h
2
2 ( x + h ) − 3 − ( 2x − 3)
2
lim
h→0 h
2 2 2
2x + 4xh + 2h − 3 − 2x + 3
lim
h→0 h
2
4xh + 2h
lim
h→0 h

16. 2. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
2
f ( x ) = 2x − 3 P (1,−1)
2
4xh + 2h
lim
h→0 h
h ( 4x + 2h )
lim
h→0 h
lim ( 4x + 2h )
h→0
4x
at (1,−1) : 4
y + 1 = 4 ( x − 1)

17. 3. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
f ( x) = x + 6 P ( 3, 3)
f ( x + h) − f ( x)
lim
h→0 h
x+h+6 − x+6
lim
h→0 h
x+h+6 − x+6 x+h+6 + x+6
lim g
h→0 h x+h+6 + x+6
x+h+6− x−6
lim
h→0
h ( x+h+6 + x+6 )

18. 3. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
f ( x) = x + 6 P ( 3, 3)
x+h+6− x−6
lim
h→0
h ( x+h+6 + x+6 )
1
lim
h→0 x+h+6 + x+6
1
2 x+6

19. 3. Find the equation of the tangent line to
the curve at P. Use Point-Slope form.
f ( x) = x + 6 P ( 3, 3)
1 1 1
at P : → →
2 x+6 2 3+ 6 6
1
y − 3 = ( x − 3)
6

20. HW #3
"I hear and I forget.
I see and I remember.
I do and I understand." -- Chinese Proverb.
“DO PROBLEMS!” -- Mr. Wright