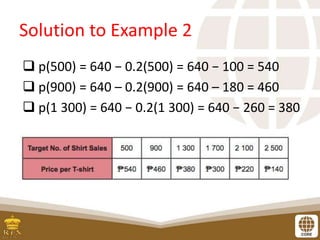
This document discusses evaluating functions by substituting values for variables. It provides examples of evaluating various functions, including price functions. Students should be able to evaluate functions and solve problems involving function evaluation. Functions can be even, odd, or neither based on whether f(-x) = f(x) or f(-x) = -f(x). Examples are provided to identify functions as even, odd, or neither. Exercises include evaluating functions for given values and determining function parity.

1. Evaluating Functions
General Mathematics

2. Lesson Objectives
At the end of the lesson, the students must be
able to:
• evaluate a function; and
• solve problems involving evaluation of
functions.

3. Law of Substitution
If a + x = b and x = c, then a+ c= b
Illustration:
To find the value of n2 when n is 15: Substitute
15 in place of n in n2 to get 152 or 225.

4. Evaluating Functions
To evaluate function is to replace its variable
with a given number or expression.
Think of the domain as the
set of the function’s input
values and the range as the
set of the function’s output
values as shown in the figure
below. The input is
represented by x and the
output by f(x).

5. Example 1
If f(x) = x + 8, evaluate each.
a. f(4)
b. f(–2)
c. f(–x)
d. f(x + 3)

6. Solution to Example 1
a. f(4) = 4 + 8 or 12.
b. f(–2) = –2 + 8 or 6
c. f(–x) = –x + 8
d. f(x + 3) = x + 3 + 8 or x + 11

7. Example 2
The price function p(x) = 640 – 0.2(x) represents
the price for which you can sell x printed T-
shirts.
What must be the price of the shirt for the first
3 entries in the table?
Target No. of Shirt Sales 500 900 130
0
170
0
2100 2500
Price per T-shirt

8. Solution to Example 2
 p(500) = 640 − 0.2(500) = 640 − 100 = 540
 p(900) = 640 – 0.2(900) = 640 – 180 = 460
 p(1 300) = 640 − 0.2(1 300) = 640 − 260 = 380

9. Even and Odd Functions
The function f is an even function if and only if
f(–x) = f(x),for all x in the domain of f.
The function f is an odd function if and only if
f(–x) = –f(x), for all x in the domain of f.

10. Example 3
Identify each function as even, odd, or neither.
a. f(x) = x5
b. g(x) = 3x4 – 2x2
c. h(x) = x2+ 3x + 1

11. Solution to Example 3
a. f(x) = x5 Since f(–x) =
–f(x),
f(–x) = (–x)5 f is an odd function.
= –x5
b. g(x) = 3x4 – 2x2 Since g(–x) = g(x),
g(–x) = 3(–x)4 – 2(–x)2 g is an even function.
= 3x4 – 2x2
b. h(x) = x2+ 3x + 1

12. Solution to Example 3
c. h(x) = x2+ 3x + 1
h(–x) = (–x)2 + 3(–x) + 1
= x2 – 3x + 1
Only the second term changed sign when x was
replaced by –x. Thus, h is neither even nor odd.

13. Exercise A
Evaluate each function at the indicated values of
the independent variable and simplify the result.
1. f(x) = 9 – 6x f(–1)
2. g(x) = x2 – 4x g(2 – x)
3. h(x) =2x h (1/2)
4. f(x) = –2x2 – 3 f(–3)
5. f(x) = √9 − x2 f(3)

14. Exercise B
The function C described by C(F) = 5/9(F − 32)
gives the Celsius temperature corresponding to
the Fahrenheit temperature F.
1. Find the Celsius temperature equivalent to
14°F.
2. Find the Celsius temperature equivalent to
68°F.

15. Exercise C
Determine whether or not each function is
even, odd, or neither.
1. f(x) = x3 – 1
2. g(x) = 2x4+ 3x2+ 1
3. h(x) = 3x3– 4x5
4. h(x) = x4– x2
5. g(x) = 2x4+ 3x2+ 1