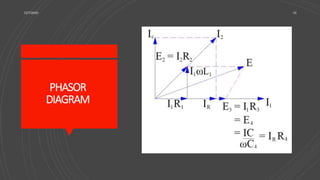
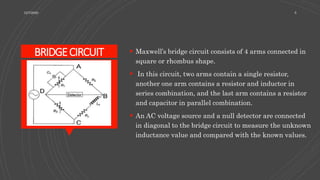
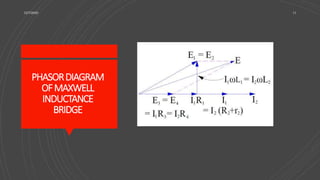
The Maxwell Bridge is an advanced form of the Wheatstone Bridge used to measure self-inductance in circuits through the null deflection method, comparing known and unknown inductance values. The bridge operates on principles of resonance and utilizes specific formulas for balanced conditions to determine unknown inductance and resistance. It has applications in various electronic and communication systems but also has limitations regarding high-quality factors and cost of components.

1. MAXWELL BRIDGE
KAROLINEKERSIN.E
Asst.prof /BMIE

2. MAXWELL
BRIDGE
 The bridge used for the measurement of self-
inductance of the circuit is known as the
Maxwell bridge.
 It is the advanced form of the Wheatstone
bridge.
 A Maxwell bridge uses the null deflection
method (also known as the “bridge method”) to
calculate an unknown inductance in a circuit.
 When the calibrated components are a parallel
capacitor and resistor, the bridge is known as a
Maxwell-Wien bridge.
12/7/2020 2

3. PRINCIPLE
 It works on the principle of comparison of known and unknown
inductance values.
 The working principle is that the positive phase angle of an
inductive impedance can be compensated by the negative
phase angle of a capacitive impedance when put in the opposite
arm and the circuit is at resonance (i.e., no potential difference
across the detector and hence no current flowing through it).
 The unknown inductance then becomes known in terms of this
capacitance.
12/7/2020 3

4. MAXWELL
BRIDGE
FORMULA
 If the maxwell’s bridge is in balance condition, the
unknown inductance can be measured by using a
variable standard capacitor. The maxwell’s bridge
formula is given as (in terms of inductance, resistance,
and capacitance)
 R1 = R2R3/R4
 L1= R2R3C4
The quality factor of Maxwell’s bridge circuit is given as,
Q = ωL1/R1 = ωC4R4
12/7/2020 4

5. BRIDGECIRCUIT  Maxwell’s bridge circuit consists of 4 arms connected in
square or rhombus shape.
 In this circuit, two arms contain a single resistor,
another one arm contains a resistor and inductor in
series combination, and the last arm contains a resistor
and capacitor in parallel combination.
 An AC voltage source and a null detector are connected
in diagonal to the bridge circuit to measure the unknown
inductance value and compared with the known values.
12/7/2020 5

6. TYPESOF
MAXWELL’S
BRIDGE
 Two methods are used for determining the self-
inductance of the circuit. They are
 Maxwell’s Inductance Bridge
 Maxwell’s inductance Capacitance Bridge
12/7/2020 6

7. MAXWELL
INDUCTANCE
BRIDGE
 In such type of bridges, the value of unknown resistance
is determined by comparing it with the known value of
the standard self-inductance.
12/7/2020 7

8. In the circuit,
 L1 = Unknown inductance having resistance R1
 L2 = Variable standard inductance with fixed resistance r2
 R2 = Variable resistance
 R3 and R4 = Known resistance
Impedance of arm ab, Z1 = (R1+jwL1)
Impedance of arm cd, Z2 = R4
Impedance of arm ad, Z3 = (R2+r2+jwL2)
Impedance of arm bc, Z4 = R3
12/7/2020 8

9. Hence for balanced bridge,
Z1Z2 =Z3Z4
(R1+jwL1)xR4 = (R2+r2+jwL2)xR3
R1R4-R2R3-r2R3+jw(L1R4-L2R3) = 0
Equating real and imaginary part we get,
R1R4-R2R3-r2R3 = 0 ……………(1)
and (L1R4-L2R3) = 0 ……………(2)
Thus unknown inductance L1 and its resistance R1
may be calculated.
12/7/2020 9

10. From (1),
R1R4 = R2R3+r2R3
= R3(R2+r2)
Hence, R1 = (R3/R4)(R2+r2)
Now from (2),
L1R4 = L2R3
Hence, L1 = L2R3 / R4
Thus unknown inductance L1 and its
resistance R1 may be calculated.
12/7/2020 10

11. PHASORDIAGRAM
OFMAXWELL
INDUCTANCE
BRIDGE
12/7/2020 11

12. MAXWELLINDUCTANCE
CAPACITANCEBRIDGE
 In this method, the unknown inductance is measured
by comparison with standard known capacitance.
12/7/2020 12

13. In the above diagram,
 L1 = Unknown inductance with resistance R1
 C4 =variable standard capacitor
 R2, R3 & R4 = Known fixed resistance
 Now,
 Impedance of arm ab, Z1 = (R1+jwL1)
 Impedance of arm cd, Z2 = R4 / (1+jwC4R4)
 Impedance of arm ad, Z3 = R2
 Impedance of arm bc, Z4 = R3
12/7/2020 13

14. For bridge to be balance,
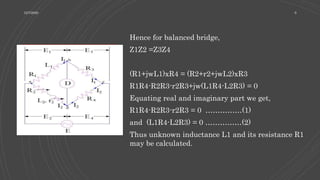
 Z1Z2 =Z3Z4
 (R1+jwL1)x [R4 / (1+jwC4R4)] = R2R3
 R1R4-R2R3 +jw(L1R4-R2R3C4R4) = 0
 Equating real and imaginary parts we get,
 R1 = R2R3 / R4
 and L1 = R2R3C4
12/7/2020 14

15. QUALITYFACTOR
 The quality factor of inductor may also be calculated as
 Q = wL1/R1
 = wR2R3C4 / R1
 Since R4 = R2R3C4 / R1 , hence
 Q = wC4R4
12/7/2020 15

16. PHASOR
DIAGRAM
12/7/2020 16

17. ADVANTAGE
 The expression of inductance is independent of
frequency.
 A wide range of inductance can be measured at power
and audio frequencies.
 The expression for inductance is simple and can easily
be calculated.
12/7/2020 17

18. DISADVANTAGE
 The fixed capacitor in Maxwell’s bridge circuit
may create interaction between resistance and
reactance balance.
 It is not suitable to measure a high range of
quality factor ( Q values >=10)
 The variable standard capacitor used in the
circuit is very costly.
 It is not used to measure the low-quality factor (
Q value) due to the circuit balance condition.
Hence it is used for medium quality coils.
12/7/2020 18

19. APPLICATIONS
 Used in communication systems
 Used in electronic circuits
 Used in power and audio frequency circuits
 Used to measure unknown inductance values of the
circuit and compared with a standard value.
 Used to measure medium quality coils.
 Used in filter circuits, instrumentation, linear and non-
linear circuits
 Used in power conversion circuits.
12/7/2020 19

20. THANK YOU
12/7/2020 20