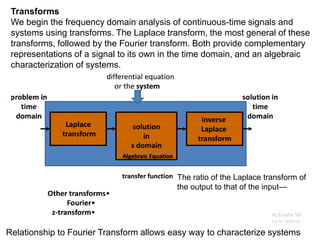
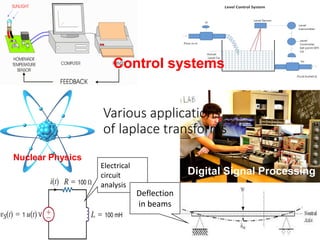
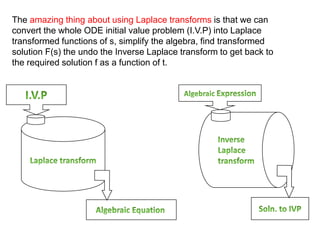
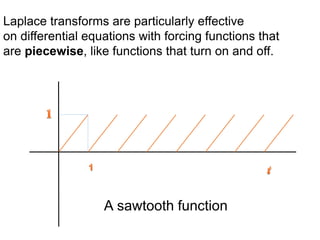
The document discusses Laplace transforms, which convert functions of time into functions of frequency to make differential equations easier to solve. Laplace transforms are useful for solving complex differential equations by converting them into simpler polynomial equations. The document also outlines several applications of Laplace transforms in fields like control systems, signal processing, physics, and circuit analysis.

1. Laplace Transforms and
it’s Applications

3. What is Laplace transform ?
Basically, a Laplace transform will convert a function in some
domain into a function in another domain, without changing
the value of the function.
For example
let’s take this function where a Laplace transform is used to
convert a function of time to a function of frequency.
L {cos(wt)} = s / (s² + w²)
A Laplace transform is a type of integral transform

4. Why do we use Laplace Transform ?
•We use Laplace transform to convert equations having
complex differential equations to relatively simple
equations having polynomials. Since equations having
polynomials are easier to solve, we use Laplace
transform to make calculations easier.
Laplace transforms are invaluable for any engineer’s
mathematical toolbox as they make solving linear ODEs and
related initial value problems, as well as systems of linear
ODEs, much easier.

5. • With Laplace transform nth degree differential equation can
be transformed into an nth degree polynomial. One can easily
solve the polynomial to get the result and then change it into
a differential equation using inverse Laplace transform.

6. Relationship to Fourier Transform allows easy way to characterize systems
The ratio of the Laplace transform of
the output to that of the input—
Transforms
We begin the frequency domain analysis of continuous-time signals and
systems using transforms. The Laplace transform, the most general of these
transforms, followed by the Fourier transform. Both provide complementary
representations of a signal to its own in the time domain, and an algebraic
characterization of systems.

7. The Laplace transform depends on a complex variable
s = σ + jΩ, composed of damping σ and frequency Ω , while the
Fourier transform considers only frequency Ω.
■ Damping and frequency characterization of continuous-time
signals:
The growth or decay of a signal— damping—as well as its
repetitive nature—frequency—in the time domain ,are
characterized in the Laplace domain (s domain)by the location
of the roots of the numerator and denominator, or zeros and
poles, of the Laplace transform of the signal.
s-plane

j





0



8. Some other Uses of Laplace transform
• The Laplace transform provides a significant algebraic characterization of
continuous-time systems: The ratio of the Laplace transform of the output
to that of the input—or the transfer function of the system.
• In so doing, it also transforms the main differential equation into an
algebraic equation which is often easier to analyze.
• The Laplace transform unifies the convolution integral and the differential
equations system representations.
The concept of transfer function is not only useful in analysis but also in
design.
• Laplace Transform systems have the very important property that if the
input to the system is sinusoidal, then the output will also be sinusoidal at
the same frequency but in general with different magnitude and phase.
These magnitude and phase differences as a function of frequency are
known as the frequency response of the system.

9. Various applications
of laplace transforms
Nuclear Physics
Control systems
Digital Signal Processing
Electrical
circuit
analysis
Deflection
in beams

10. The amazing thing about using Laplace transforms is that we can
convert the whole ODE initial value problem (I.V.P) into Laplace
transformed functions of s, simplify the algebra, find transformed
solution F(s) the undo the Inverse Laplace transform to get back to
the required solution f as a function of t.

11. Application in digital signal processing
Application in digital signal processing
A simple Laplace transform is conducted while
sending signals over two-way communication
medium (FM/AM stereos, 2 way radio sets,
cellular phones.)
When information is sent over medium such as
cellular phones, they are first converted into
time-varying wave and then it is super imposed
on the medium. In this way, the information
propagates. Now, at the receiving end, to
decode the information being sent, medium
wave’s time functions are converted to
frequency functions. This is a simple example of
Laplace transform in real life.

12. 1
A sawtooth function
Laplace transforms are particularly effective
on differential equations with forcing functions that
are piecewise, like functions that turn on and off.

13.  Consider the following piecewise-defined function f.
 From this definition of f, and from the graph of f below, we see
that f is piecewise continuous on [0, 3].














3
2
1
2
1
,
3
1
0
,
)
(
2
t
t
t
t
t
t
t
f
Example 1

14.  Consider the following piecewise-defined function f.
 From this definition of f, and from the graph of f below, we
see that f is not piecewise continuous on [0, 3].
Example 2
 















3
2
,
4
2
1
,
2
1
0
,
1
)
(
1
2
t
t
t
t
t
t
f

15. In practice, Laplace transforms and inverse Laplace transforms are
obtained using tables and computer algebra systems.