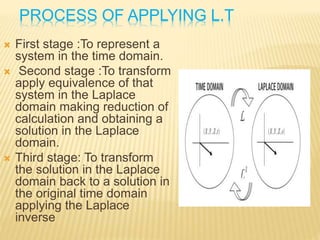
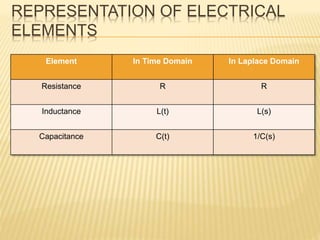
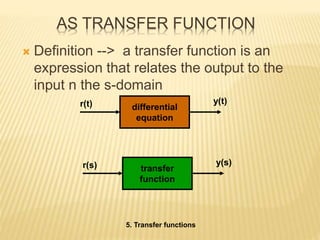
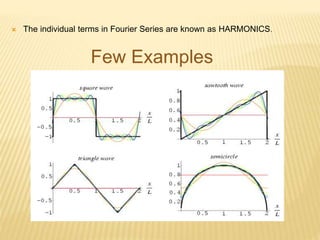
This document discusses different mathematical concepts including Laplace transforms, Fourier series, and their applications. It defines Laplace transforms as a linear operator that transforms a function of time into a function of complex variables. Laplace transforms can be used to solve differential equations by converting them into algebraic equations. Fourier series represent periodic functions as the sum of simple sine and cosine terms. Both Laplace transforms and Fourier series have applications in electrical engineering for analyzing circuits, signals, and systems. Overall, the document outlines important mathematical concepts and their uses in engineering problems.

1. By :
T.ANIL KUMAR(14A81A0237)&
S HEMANTH DURGA REDDY(14A81A0236)
SRI VASAVI ENGINEERING COLLEGE
TADEPALLIGUDEM
B.Tech 3rd year EEE

2. WHAT IS MATHS ?
In Ramanujan’s point of view maths
is defined as “A pattern connected
with Calculus, Geometry,
Trignomentry and etc., combined
together to form a solution

3. CREATIVITY HOLDS TWO THINGS
Engineering + Maths = Everything
Enginnering – Maths = Nothing

4. DIFFERENT METHODS IN MATHS
 Laplace transforms
 Calculus
 Z- transforms
 Complex numbers
 Probability
 Fourier series
 Limits
 Trigonometry etc....

5. LAPLACE TRANSFORMS

6. THE FRENCH NEWTON
PIERRE-SIMON LAPLACE
 Transformation in mathematics deals with
the conversion of one function to another
function that may not be in the same
domain.
 Laplace transform is a powerful
transformation tool, which literally
transforms the original differential
equation into an elementary algebraic
expression.
 This transform is named after the
mathematician and renowned astronomer
Pierre Simon Laplace who lived in
France.

7. DEFINITION
 The Laplace transform is a linear operator
that switched a function f(t) to F(s).
 Specifically:
where:
{ ( )}f tL =F(s)
t domain s domain

8. PROCESS OF APPLYING L.T
 First stage :To represent a
system in the time domain.
 Second stage :To transform
apply equivalence of that
system in the Laplace
domain making reduction of
calculation and obtaining a
solution in the Laplace
domain.
 Third stage: To transform
the solution in the Laplace
domain back to a solution in
the original time domain
applying the Laplace
inverse

9. REPRESENTATION OF ELECTRICAL
ELEMENTS
Element In Time Domain In Laplace Domain
Resistance R R
Inductance L(t) L(s)
Capacitance C(t) 1/C(s)

10. AS TRANSFER FUNCTION
 Definition --> a transfer function is an
expression that relates the output to the
input n the s-domain
differential
equation
r(t) y(t)
transfer
function
r(s) y(s)
5. Transfer functions

11. APPLICATIONS OF LAPLACE TRANSFORMS
 Electrical circuits
 Control Systems
 Signals & Systems

12. FOURIER SERIES
 Introduced by JOSEPH
FOURIER
 DEF:-A way to represent a
(wave-like) function as the
sum of simple sine waves.

13. Fourier series make use of the orthogonality relationships
of the sine and cosine functions.
FOURIER SERIES can be generally written as,
Where,
……… (1.1)
……… (1.2)
……… (1.3)

14.  The individual terms in Fourier Series are known as HARMONICS.
Few Examples

15. APPLICATIONS
 Used in Harmonic Analysis
 Transient Analysis
 Conversion of Response from Time
Domain to Frequency Domain
 Power Electronics

16. Electrical Engineering (A.C. Circuits):
 Resistors, inductors, capacitors, power
engineering, analysis of electric magnetic
fields and their interactions with materials
and structures.

17. CONCLUSION
Machines Rule The World We Rule
The Machines Without Calculations
There Are No Machines

18. REFERENCES
 WWW.WIKIPEDIA.COM
 WWW.SCRIBD.COM