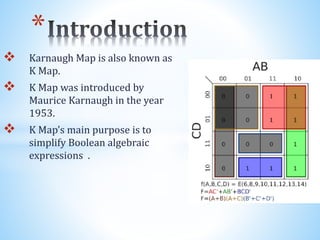
The document discusses Karnaugh maps, which are used to simplify Boolean algebraic expressions. It describes the basics of Karnaugh maps including their introduction in 1953, how they can simplify sum of products and product of sums expressions, their properties for two and three variable maps, and the rules for grouping cells in maps. Advantages are their simplicity and reducing costs. Applications include simplifying circuits.

1. By
-Abhijit H Jadhav (Roll no 02)
*Karnaugh Map

2.  Introduction
 Sum Of Product
 Product of Sum
 Properties
 Types
 Two Variable
 Three Variable
 Rules
 Advantages and disadvantages
 Application
 Biblography
*

3.  Karnaugh Map is also known as
K Map.
 K Map was introduced by
Maurice Karnaugh in the year
1953.
 K Map’s main purpose is to
simplify Boolean algebraic
expressions .
*

4.  A Sum Of Product expression can always be
implemented using AND gates.
 The Sum Of Product represents the High value i.e ( 1
) .
 Example:
f (A,B,C ) = AB + AC + ABC
*

5.  A Product of Sum expression can always be
implemented using OR gates.
 The Sum Of Product represents the low
value i.e ( 0 ) .
 Example:
f (A, B, C) = (A +B). (A +C).(B +C)
*

6.  IAn n-variable K-map has 2n
cells with n-variable
truth table value.
 Adjacent cells differ
in only one bit .
 Each cell refers to a
minterm or maxterm.
 For min term mi ,
max term Mi and
don’t care of f we
place 1 , 0 , x .
*

7. 1. Groups may not include any cell containing a zero
2. Groups may be horizontal or vertical, but not
3. diagonal.
4. Groups must contain 1, 2, 4, 8, or in general 2n cells.
That is if n = 1, a group will contain two 1's since 21 =
2.
5. If n = 2, a group will contain four 1's since 22 = 4
6. Each group should be as large as possible.
7. Each cell containing a one must be in at least one
group
8. Groups may overlap
9. Groups may wrap around the table.
10. There should be as few groups as possible, as long as
this does not contradict any of the previous rules.
*

8.  K Map Having Two Variable.
 K map having three Variable.
*

9.  Steps for solving the K map with (two variable):
1.Mark the Expansion in the Tabular form
f (A,B) = ∑m (1,2,3)
2. Form the groups of 2 or 4.
3. For the equation for output.
=B+A
*
B A 0 1
0 1
1 1 1

10.  Step are followed same as for two Variable:
*

11.  Data representation’s simplicity.
 Easy and Convenient to implement.
 Reduces the cost and quantity of logical gates.
 Less number of steps when compared to
algebraic minimization technique.
 Does not demand for the knowledge of boolean
algebraic theorems.
*
* Complexity of K-map simplification process increases
with the increase in the number of variables.

12.  Demonstrating concepts used in computer
Program to simplify large circuit.
 Visualizing concepts related to manupilating
Boolean alegebra
 Simplification of Half Adder and Full Adder
*

13.  www.wikipedia.org
 www.falstad.com
 www.microelectronics.com
 www.stelectronics.com
 www.IEEEsignalprocessing/Kmap
 www.falstad.com
*