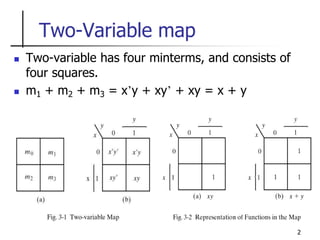
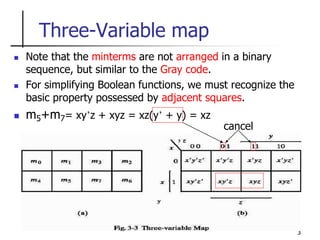
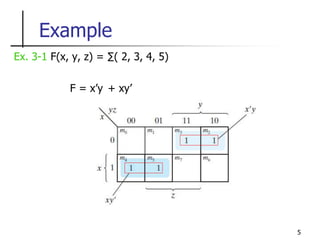
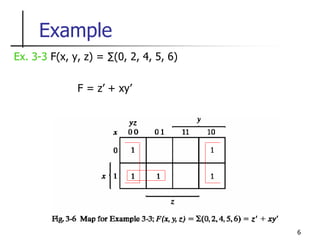
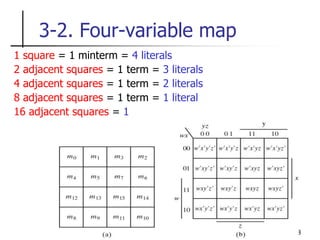
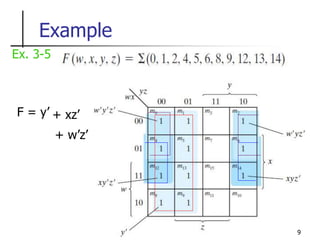
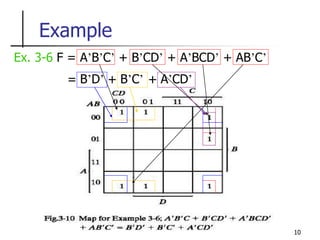
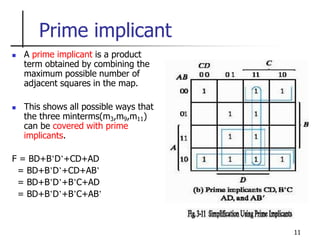
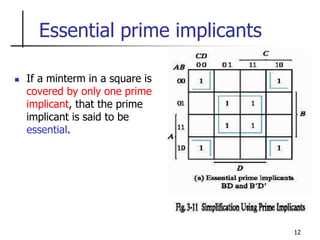
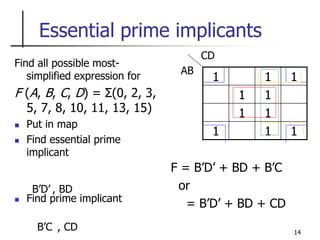
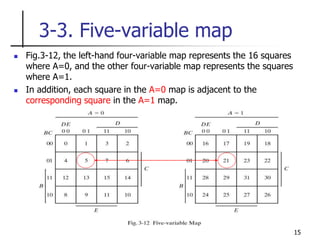
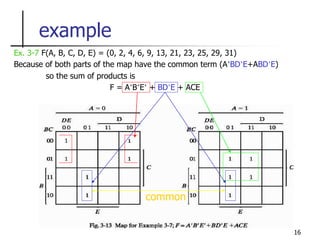
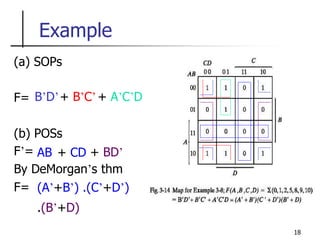
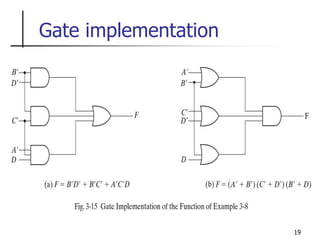
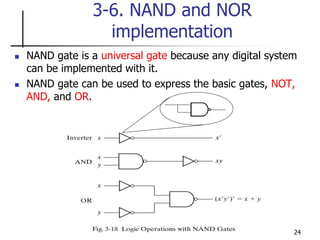
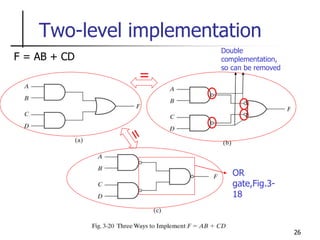
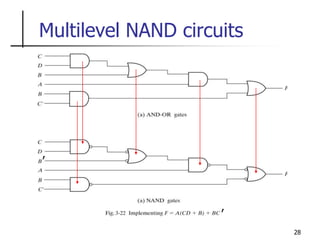
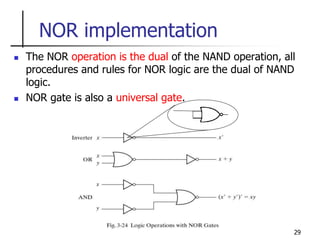
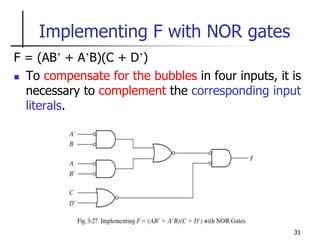
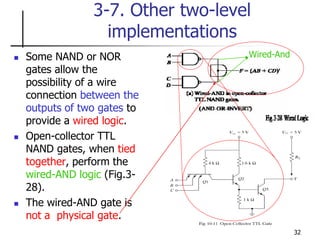
The document discusses Boolean function minimization using Karnaugh maps. It begins by introducing Karnaugh maps and how they are used to simplify Boolean functions into logic circuits with the fewest gates and inputs. Different sized Karnaugh maps are demonstrated, including two-variable, three-variable, and four-variable maps. Techniques for simplifying functions based on the number of adjacent squares in the map are described. Several examples of using Karnaugh maps to minimize Boolean functions are provided.

1. 1
Chapter 3 Gate-Level
Minimization
 The Boolean functions also can be simplified by
map method as Karnaugh map or K-map.
 The map is made up of squares, with each square
representing one minterm of the function.
 This produces a circuit diagram with a minimum
number of gates and the minimum number of
inputs to the gate.
 It is sometimes possible to find two or more
expressions that satisfy the minimization criteria.

2. 2
Two-Variable map
 Two-variable has four minterms, and consists of
four squares.
 m1 + m2 + m3 = x’y + xy’ + xy = x + y

3. 3
Three-Variable map
 Note that the minterms are not arranged in a binary
sequence, but similar to the Gray code.
 For simplifying Boolean functions, we must recognize the
basic property possessed by adjacent squares.
 m5+m7= xy’z + xyz = xz(y’ + y) = xz
y
cancel

4. 4
Simplification of the number of
adjacent squares
 A larger number of adjacent squares are
combined, we obtain a product term with fewer
literals.
1 square = 1 minterm = three literals.
2 adjacent squares = 1 term = two literals.
4 adjacent squares = 1 term = one literal.
8 adjacent squares encompass the entire map and
produce a function that is always equal to 1.
 It is obviously to know the number of adjacent squares is
combined in a power of two such as 1,2,4, and 8.

5. 5
Example
Ex. 3-1 F(x, y, z) = ∑( 2, 3, 4, 5)
F = x’y + xy’

6. 6
Example
Ex. 3-3 F(x, y, z) = ∑(0, 2, 4, 5, 6)
F = z’ + xy’

7. 7
Example
Ex. 3-4
(a) Express this function as a sum of minterms.
(b) Find the minimal sum-of-products expression.
F = C + A’B

8. 8
3-2. Four-variable map
1 square = 1 minterm = 4 literals
2 adjacent squares = 1 term = 3 literals
4 adjacent squares = 1 term = 2 literals
8 adjacent squares = 1 term = 1 literal
16 adjacent squares = 1

9. 9
Example
Ex. 3-5
F = y’ + xz’
+ w’z’

10. 10
Example
Ex. 3-6 F = A’B’C’ + B’CD’ + A’BCD’ + AB’C’
= B’D’ B’C’
+ A’CD’
+

11. 11
Prime implicant
 A prime implicant is a product
term obtained by combining the
maximum possible number of
adjacent squares in the map.
 This shows all possible ways that
the three minterms(m3,m9,m11)
can be covered with prime
implicants.
F = BD+B’D’+CD+AD
= BD+B’D’+CD+AB’
= BD+B’D’+B’C+AD
= BD+B’D’+B’C+AB’

12. 12
Essential prime implicants
 If a minterm in a square is
covered by only one prime
implicant, that the prime
implicant is said to be
essential.

13. Reading
 Chapter 3: 3.1, 3.2, 3.3
 Sheet 5
Ch 3 2(c,d,f), 3(c,d), 4(b, e), 5(a,c), 6(b,c), 7(a,b), 8(c), 9(a, c, e,
f), 10 (a, c, d, f)

14. 14
Essential prime implicants
Find all possible most-
simplified expression for
F (A, B, C, D) = Σ(0, 2, 3,
5, 7, 8, 10, 11, 13, 15)
 Put in map
 Find essential prime
implicant
 Find prime implicant
1 1 1
1 1
1 1
1 1 1
AB
CD
B’D’ , BD
F = B’D’ + BD + B’C
or
= B’D’ + BD + CD
B’C , CD

15. 15
3-3. Five-variable map
 Fig.3-12, the left-hand four-variable map represents the 16 squares
where A=0, and the other four-variable map represents the squares
where A=1.
 In addition, each square in the A=0 map is adjacent to the
corresponding square in the A=1 map.

16. 16
example
Ex. 3-7 F(A, B, C, D, E) = (0, 2, 4, 6, 9, 13, 21, 23, 25, 29, 31)
Because of both parts of the map have the common term (A’BD’E+ABD’E)
so the sum of products is
F = A’B’E’ + BD’E + ACE
common

17. 17
3-4. Product of sums
simplification
 If we mark the empty squares by 0’s rather than
1’s and combine them into valid adjacent squares,
we obtain the complement of the function, F’. Use
the DeMorgan’s theorem, we can get the product
of sums.
Ex.3-8 Simplify the Boolean function in
(a) sum of products
(b) product of sums
F(A, B, C, D) = ∑(0, 1, 2, 5, 8, 9, 10)

18. 18
Example
(a) SOPs
F=
(b) POSs
F’=
By DeMorgan’s thm
F=
B’D’+ B’C’+ A’C’D
AB + CD + BD’
(A’+B’) .(C’+D’)
.(B’+D)

19. 19
Gate implementation

20. 20
Exchange minterm and maxterm
 Consider the truth table
that defines the function F
in Table 3-2.
Sum of minterms
F(x, y, z) = ∑(1, 3, 4, 6)
Product of maxterms
F(x, y, z) = ∏(0, 2, 5, 7)
 In the other words, the 1’s
of the function represent
the minterms, and the 0’s
represent the maxterms.

21. 21
Exchange minterm and maxterm
 Find SOP and POS of
F(x, y, z) = ∏(0, 2, 5, 7)
 By grouping 1’s
 By grouping 0’s
SOP
POS

22. 22
3-5. Don’t care conditions
Ex.3-9 Simplify the F (w, x, y, z)= ∑(1, 3, 7, 11, 15) with
don’t-care conditions d(w, x, y, z) = ∑(0, 2, 5)
Minterms marked by 1’s
Don’t-care marked by x’s
Reminder squares marked by 0’s

23. 23
3-5. Don’t care conditions
Ex.3-9 Simplify the F (w, x, y, z)= ∑(1, 3, 7, 11, 15) with
don’t-care conditions d(w, x, y, z) = ∑(0, 2, 5)
Don’t care can be considered 1’s or 0’s to simplify function
In part (a) with minterms 0 and 2 F = yz + w’x’
In part (b) with minterm 5  F = yz + w’z

24. 24
3-6. NAND and NOR
implementation
 NAND gate is a universal gate because any digital system
can be implemented with it.
 NAND gate can be used to express the basic gates, NOT,
AND, and OR.

25. 25
Two graphic symbols for NAND
gate
 In part (b), we can place a bubble (NOT) in each
input and apply the DeMorgan’s theorem, then get
a Boolean function in NAND type.

26. 26
Two-level implementation
F = AB + CD
Double
complementation,
so can be removed
=
OR
gate,Fig.3-
18

27. 27
Multilevel NAND circuits
 To convert a multilevel AND-OR diagram into an
all-NAND diagram using mixed notation is as
follows:
1. Convert all AND gates to NAND gates with AND-invert
graphic symbols.
2. Convert all OR gates to NAND gates with invert-OR
graphic symbols.
3. Check all the bubbles in the diagram. For every bubble
that is not compensated by another small circle along the
same line, insert an inverter or complement the input
literal.

28. 28
Multilevel NAND circuits
,
,

29. 29
NOR implementation
 The NOR operation is the dual of the NAND operation, all
procedures and rules for NOR logic are the dual of NAND
logic.
 NOR gate is also a universal gate.

30. 30
Two graphic symbols for NOR
gate
 In part (b), we can place a bubble (NOT) in each
input and apply the DeMorgan’s theorem, then get
a Boolean function in NOR type.

31. 31
Implementing F with NOR gates
F = (AB’ + A’B)(C + D’)
 To compensate for the bubbles in four inputs, it is
necessary to complement the corresponding input
literals.

32. 32
3-7. Other two-level
implementations
 Some NAND or NOR
gates allow the
possibility of a wire
connection between the
outputs of two gates to
provide a wired logic.
 Open-collector TTL
NAND gates, when tied
together, perform the
wired-AND logic (Fig.3-
28).
 The wired-AND gate is
not a physical gate.
Wired-And

33. 33
Nondegenerate forms
 We consider four types of gates: AND, OR, NAND,
and NOR. These will have 16 combinations of two-
level forms.
 Eight of these combinations are said to be
degenerate forms, because they degenerate to a
single operation.
 The other eight nondegenerate forms produce an
SOPs or POSs as follows:
AND-OR  3-4 OR-AND  3-4
NAND-NAND  3-6 NOR-NOR  3-6
NOR-OR NAND-AND
OR-NAND AND-NOR

34. 34
AND-OR-INVERT implementation
 The two forms NAND-AND and AND-NOR are equivalent
forms and can be treated together.
F = (AB + CD + E)’
Shift back

35. 35
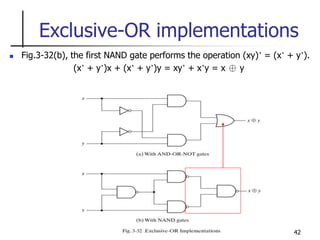
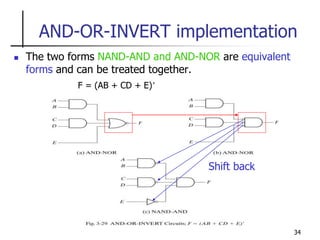
OR-AND-INVERT implementation
 The OR-NAND form resembles the OR-AND form, except for
the inversion done by the bubble in the NAND gate.
F = [(A + B)(C + D)E]’
Shift back

36. 36
Tabular summary and example
 Because of the INVERT part in each case, it is
convenient to use the simplification of F’ of the
function.

37. 37
Example
Ex.3-11 Implement the function of Fig.3-31(a) with the four
two-level forms listed in Table 3-3.
The complement of the function by combining the 0’s:
F’ = x’y + xy’ + z
The normal output for this function
F = (x’y + x’y + z)’
Which is in the AND-OR-INVERT form.

38. 38
Example
 The AND-NOR and NAND-AND implementations are
shown as follows.

39. 39
Example
 The OR-AND-INVERT forms require a simplified expression
of the complement of the function in POSs.
Combine the 1’s in the map
F = x’y’z’ + xyz’
Complement of the function
F’ = (x + y + z)(x’ + y’ + z)

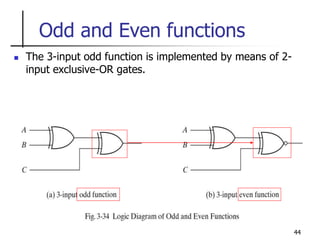
40. 40
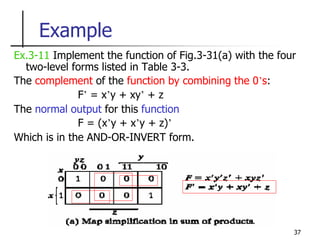
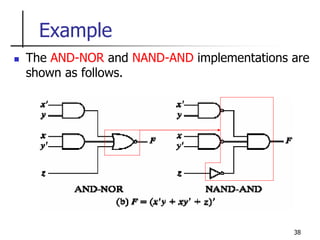
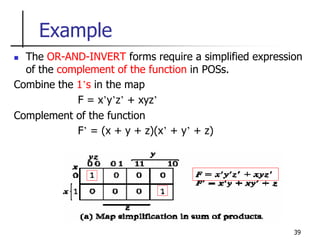
Example
The normal output F
F = (x + y + z)(x’ + y’ + z)]’
We can implement the function in the OR-NAND and NOR-OR
forms as follows.

41. 41
3-8. Exclusive-OR function
 The XOR symbol denote as ⊕, the Boolean
operation: x ⊕ y = xy’ + x’y
 The X-NOR symbol denote as ⊙, the Boolean
operation: x ⊙ y = (x ⊕ y )’ = xy + x’y’
 The identities of the XOR operation:
x ⊕ 0 = x x ⊕ 1 = x’ x ⊕ x = 0
x ⊕ x’ = 1 x ⊕ y’ = x’ ⊕ y = (x ⊕ y)’
 Commutative and associative:
A ⊕ B = B ⊕ A
(A ⊕ B) ⊕ C = A ⊕ (B ⊕ C) = A ⊕ B ⊕ C

42. 42
Exclusive-OR implementations
 Fig.3-32(b), the first NAND gate performs the operation (xy)’ = (x’ + y’).
(x’ + y’)x + (x’ + y’)y = xy’ + x’y = x ⊕ y

43. 43
Odd function
 Boolean expression of three-variable of the XOR:
A ⊕ B ⊕ C = (AB’ + A’B)C’ + (AB + A’B’)C
= AB’C’ + A’BC’ + ABC + A’B’C
=∑(1, 2, 4, 7)
 Odd function defined as the logical sum of the 2n
/2 minterms
whose binary numerical values have an odd number of 1’s.

44. 44
Odd and Even functions
 The 3-input odd function is implemented by means of 2-
input exclusive-OR gates.

45. 45
Parity generation and checking
 Table 3-4, the P make the total number of 1’s
even(including P). P constitutes an odd function.
 A parity bit is an extra bit included with a binary message to
make the number of 1’s either odd or even.
P=x ⊕ y ⊕ z

46. 46
Parity generation and checking
 The circuit that generates the parity bit in the
transmitter(receiver) is called a parity generator(checker).
Transmitter Receiver

47. 47
Example of even parity
 Since the information was
transmitted with even parity,
the four bits received must
have an even number of 1’s.
 An error occurs during the
transmission if the four bits
received have an odd number
of 1’s.
 The output of the parity
checker, denoted by C, will be
equal to 1 if an error occurs,
that is, if the four bits received
have an odd number of 1’s.
 C = x ⊕ y ⊕ z ⊕ P
Error

48. Reading
 Chapter 3: 3.4, 3.5, 3.6 , 3.7, 3.8
 Sheet 5
Ch 3 11, 12, 13(b,d), 14, 15(a,c), 16(b, c), 17, 18,19(b), 20, 23,
24, 26, 30,
31(b,e), 32(a,f), 33, 34, 35, 36, 37, 38, 39