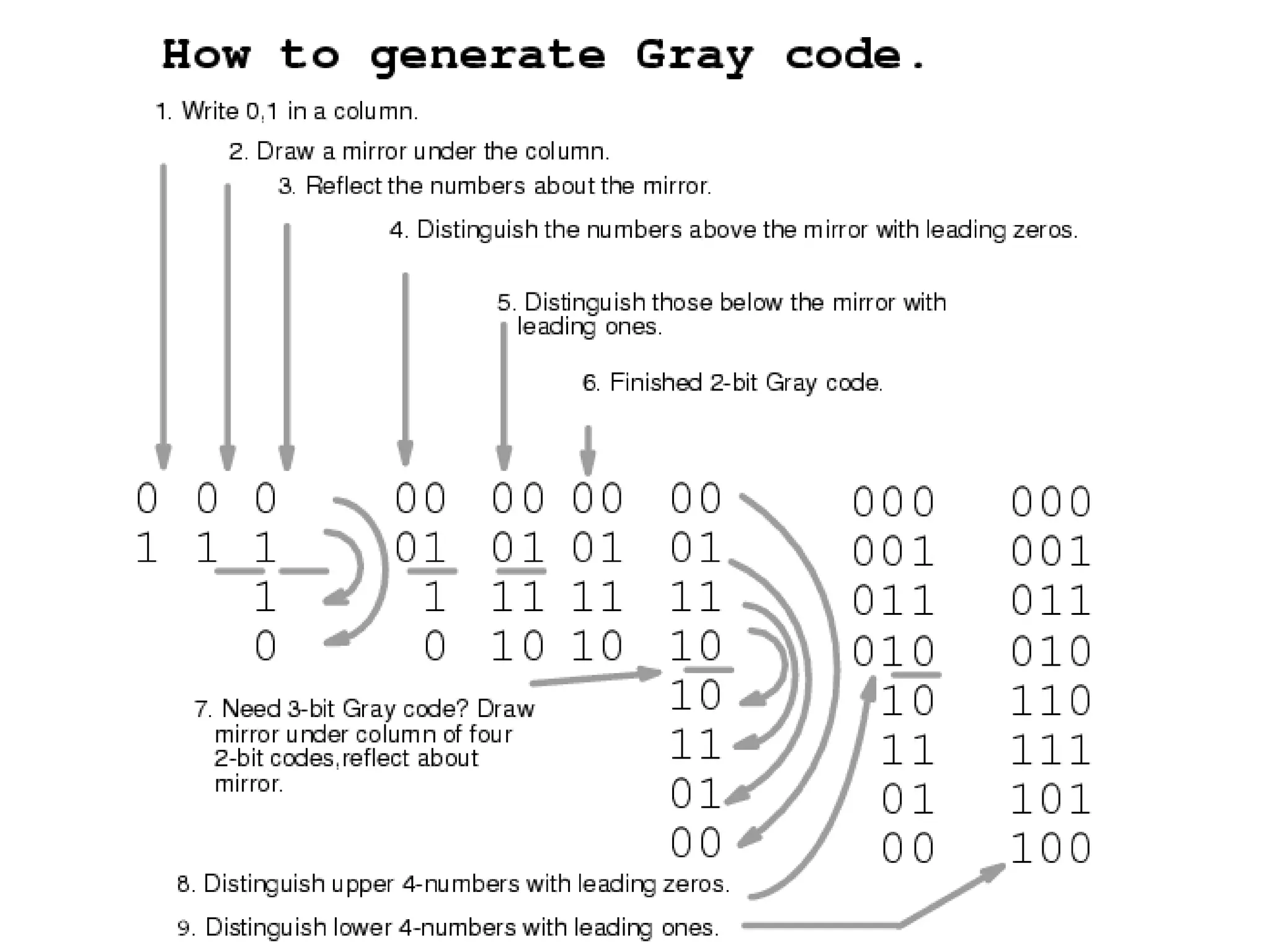
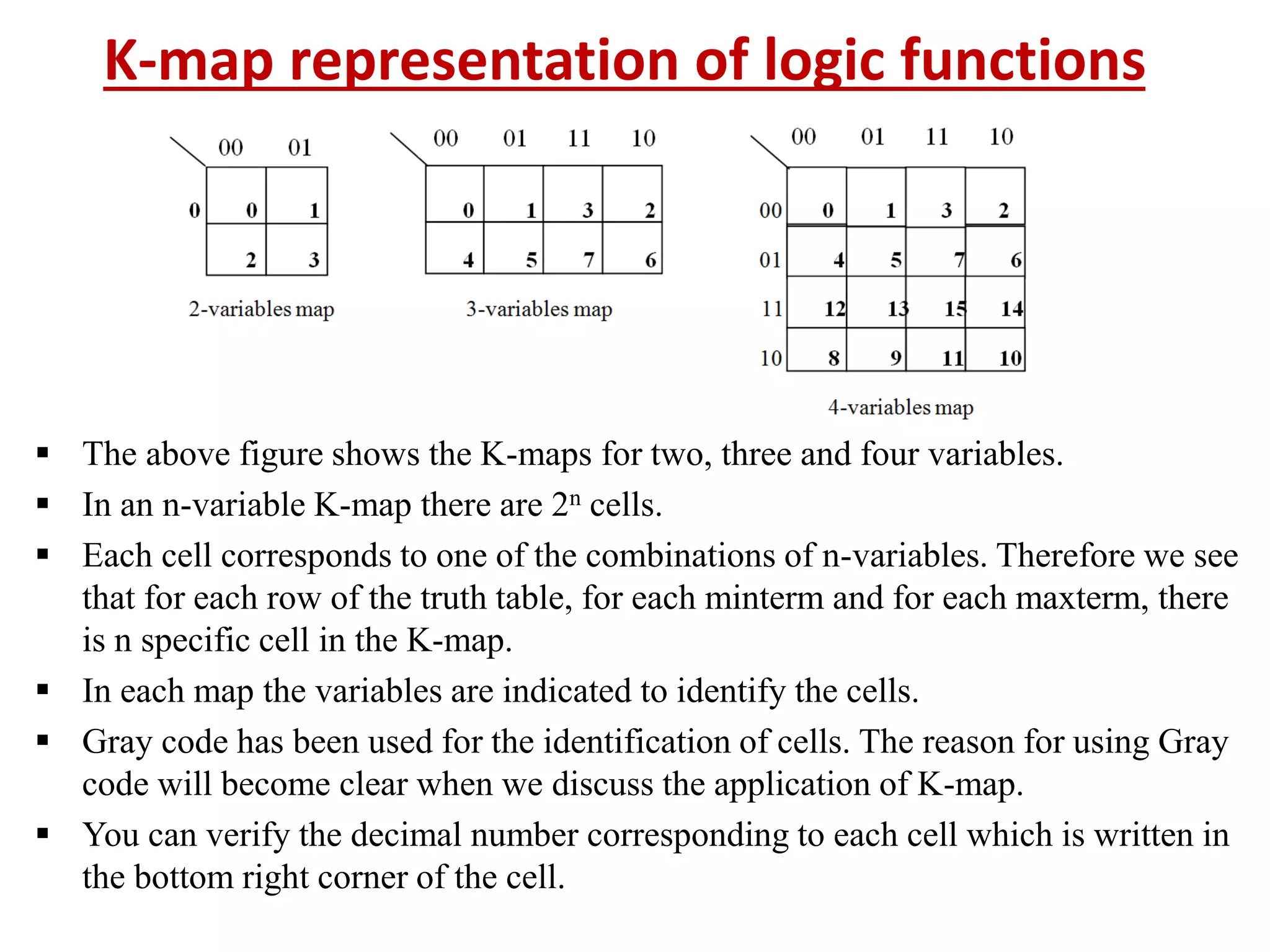
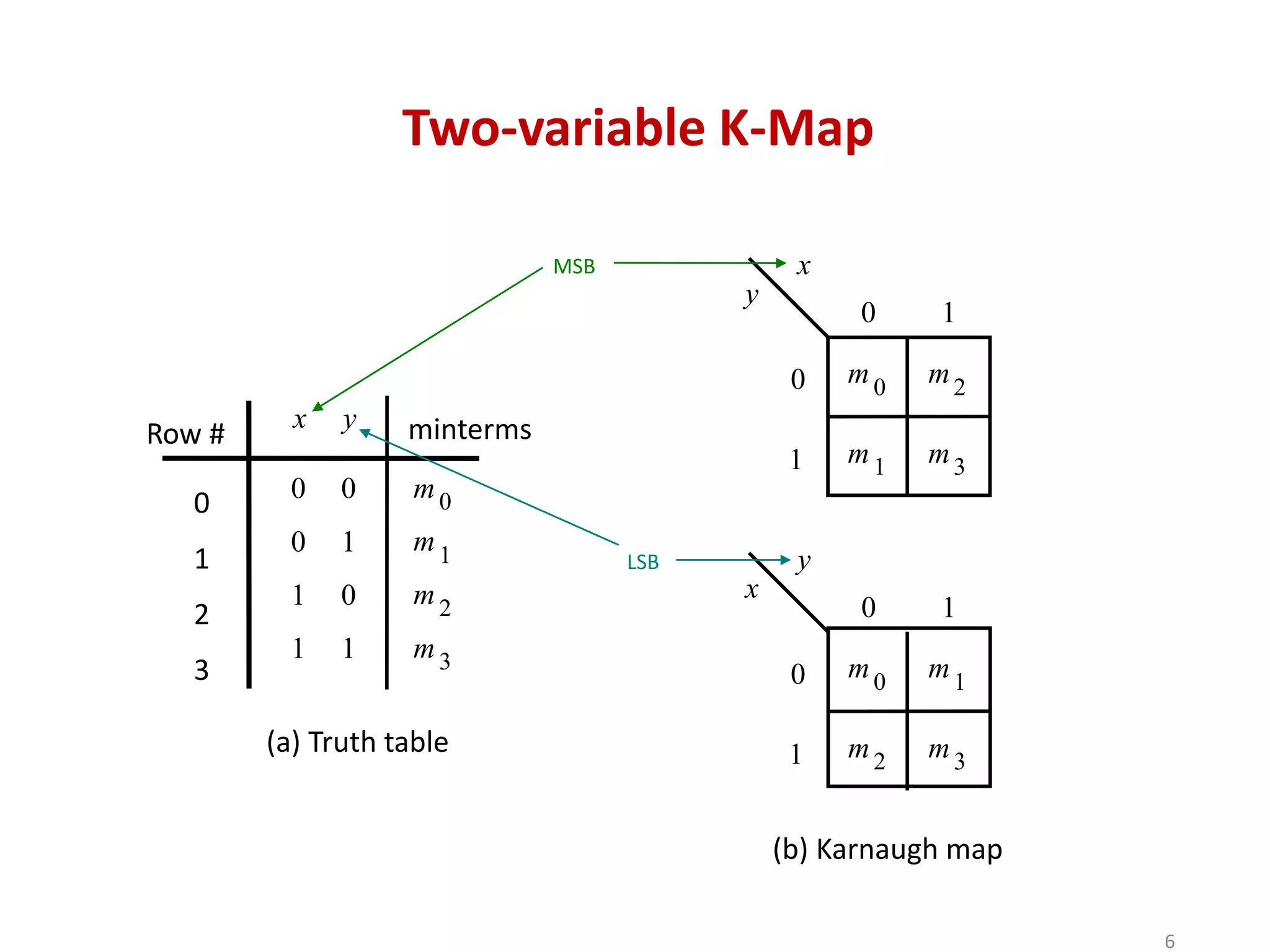
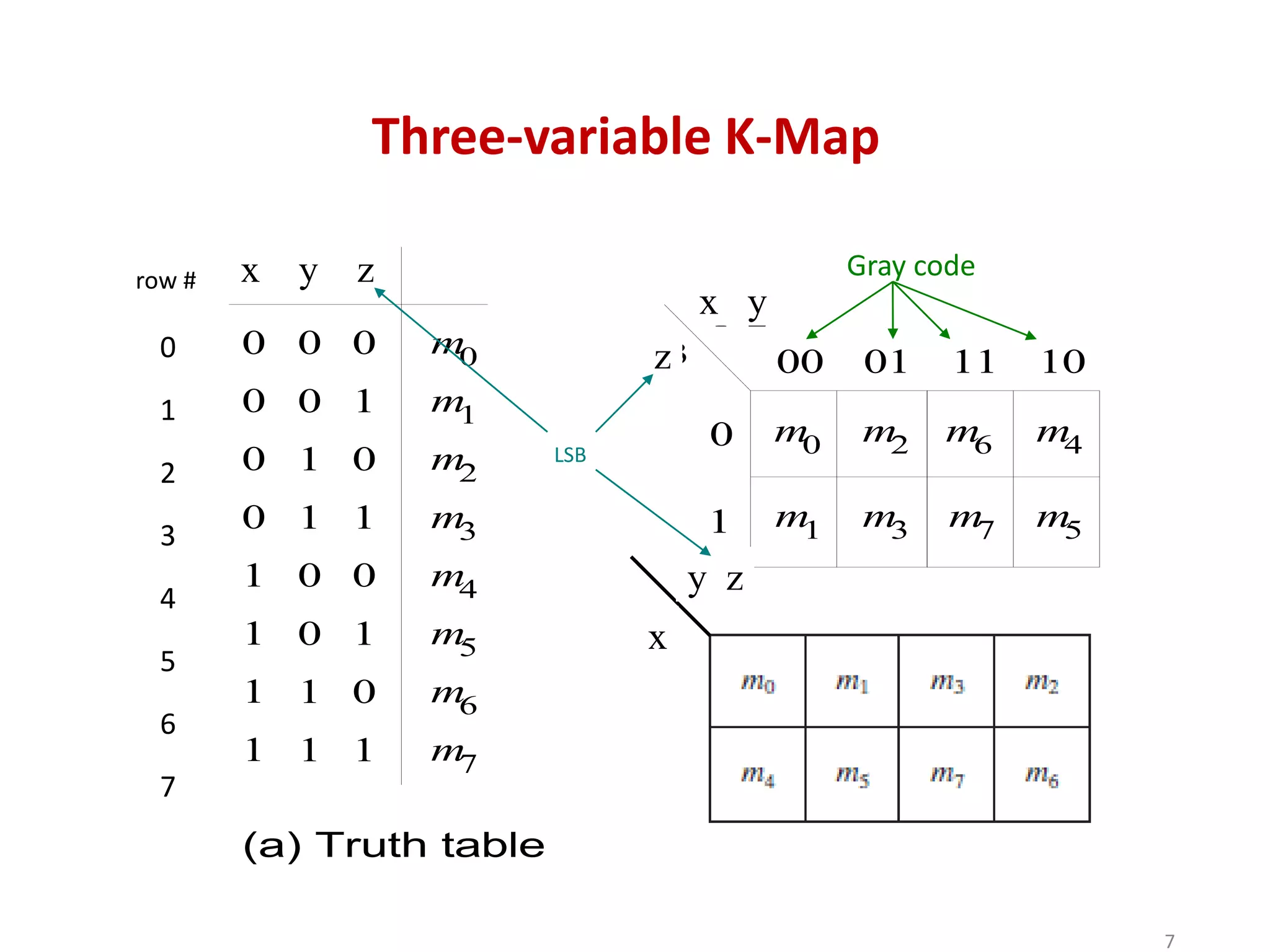
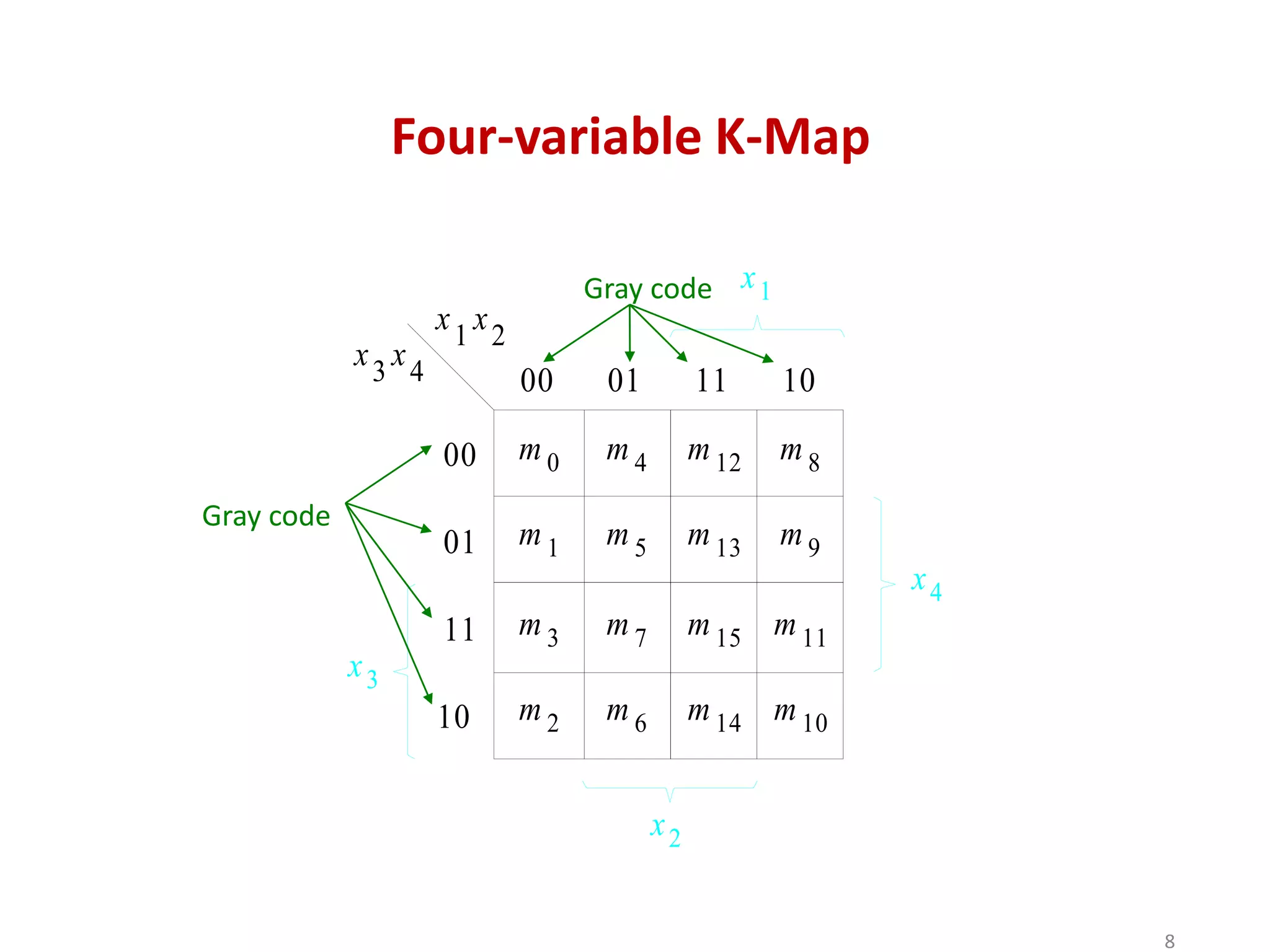
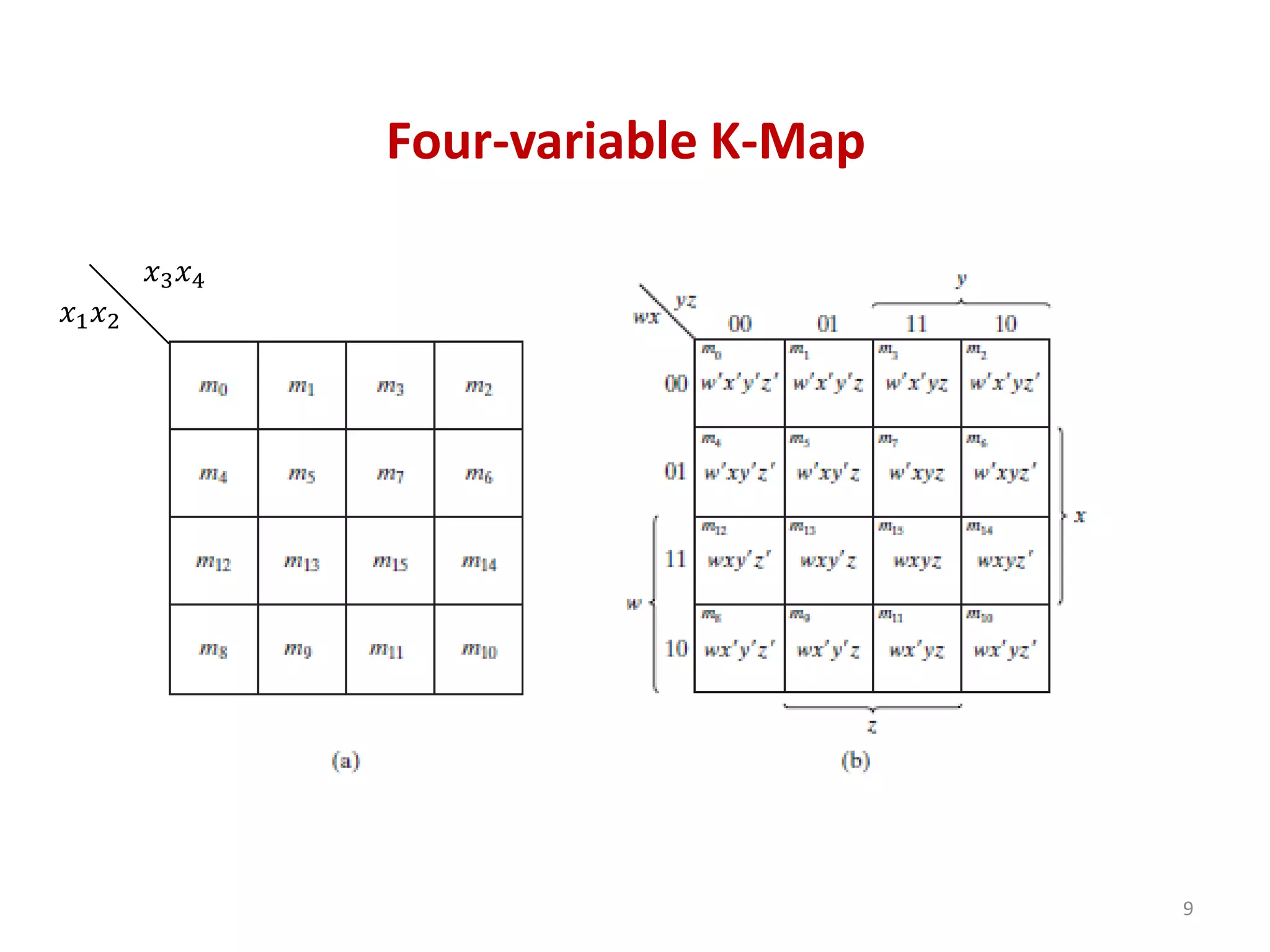
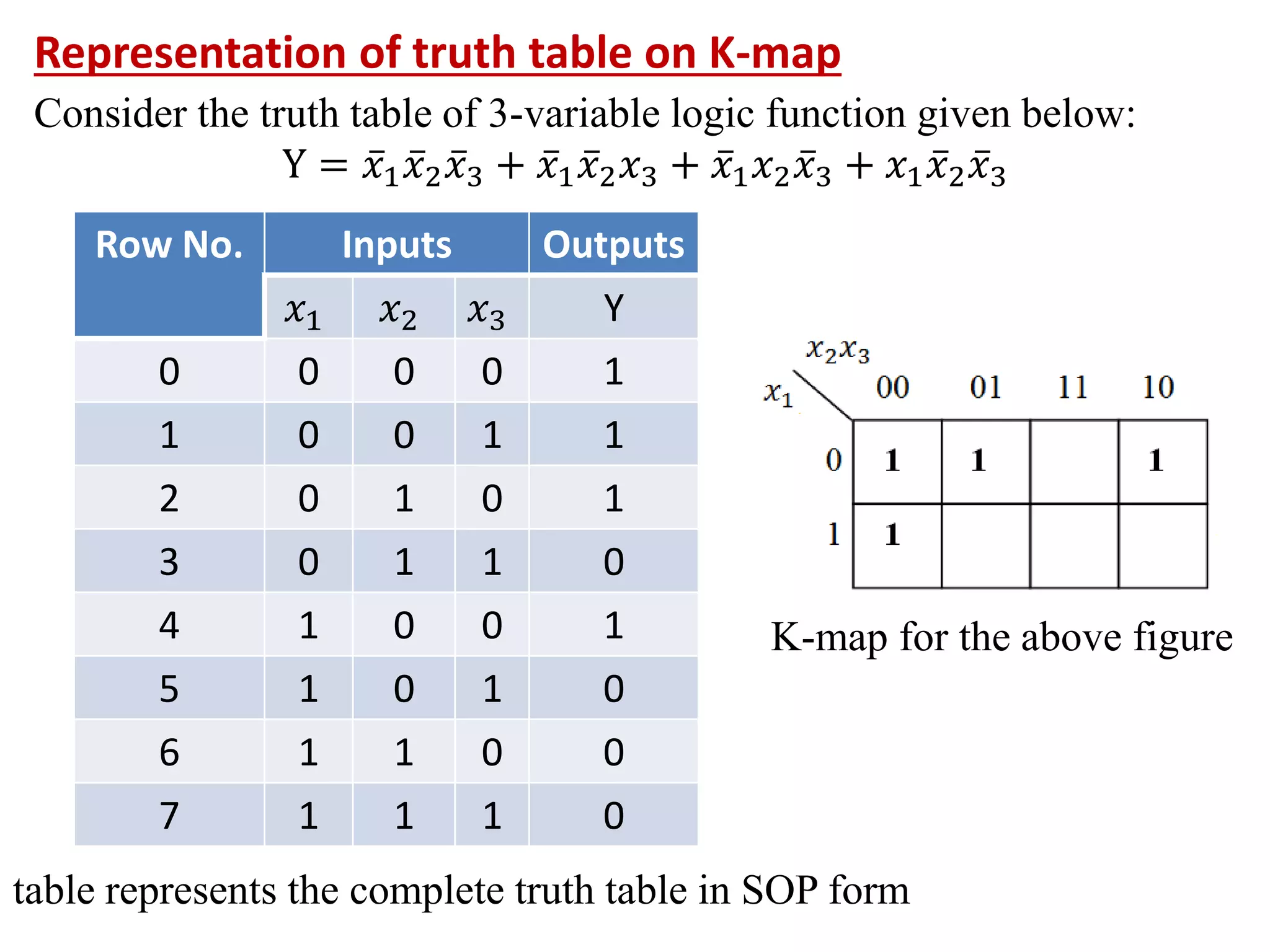
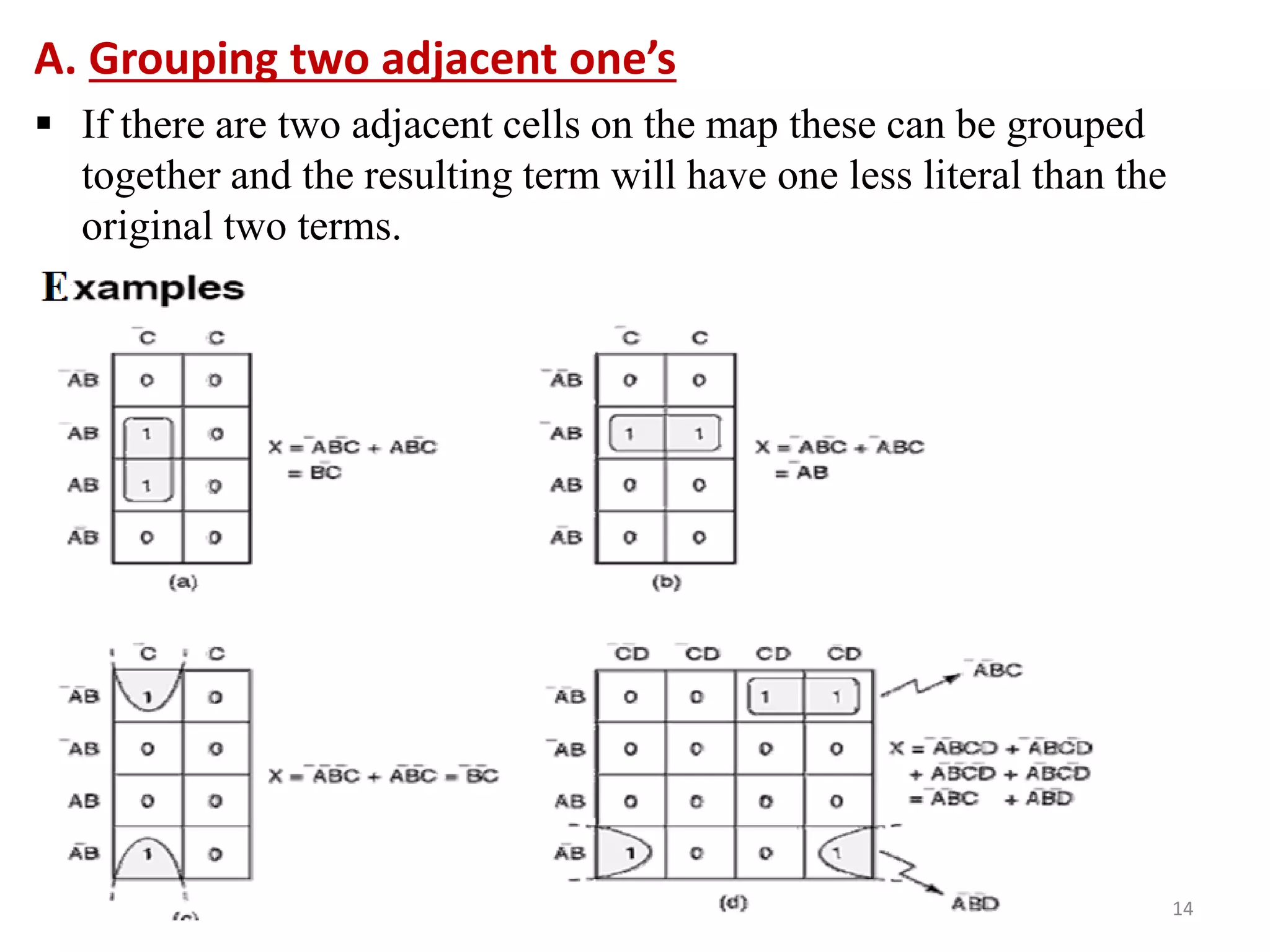
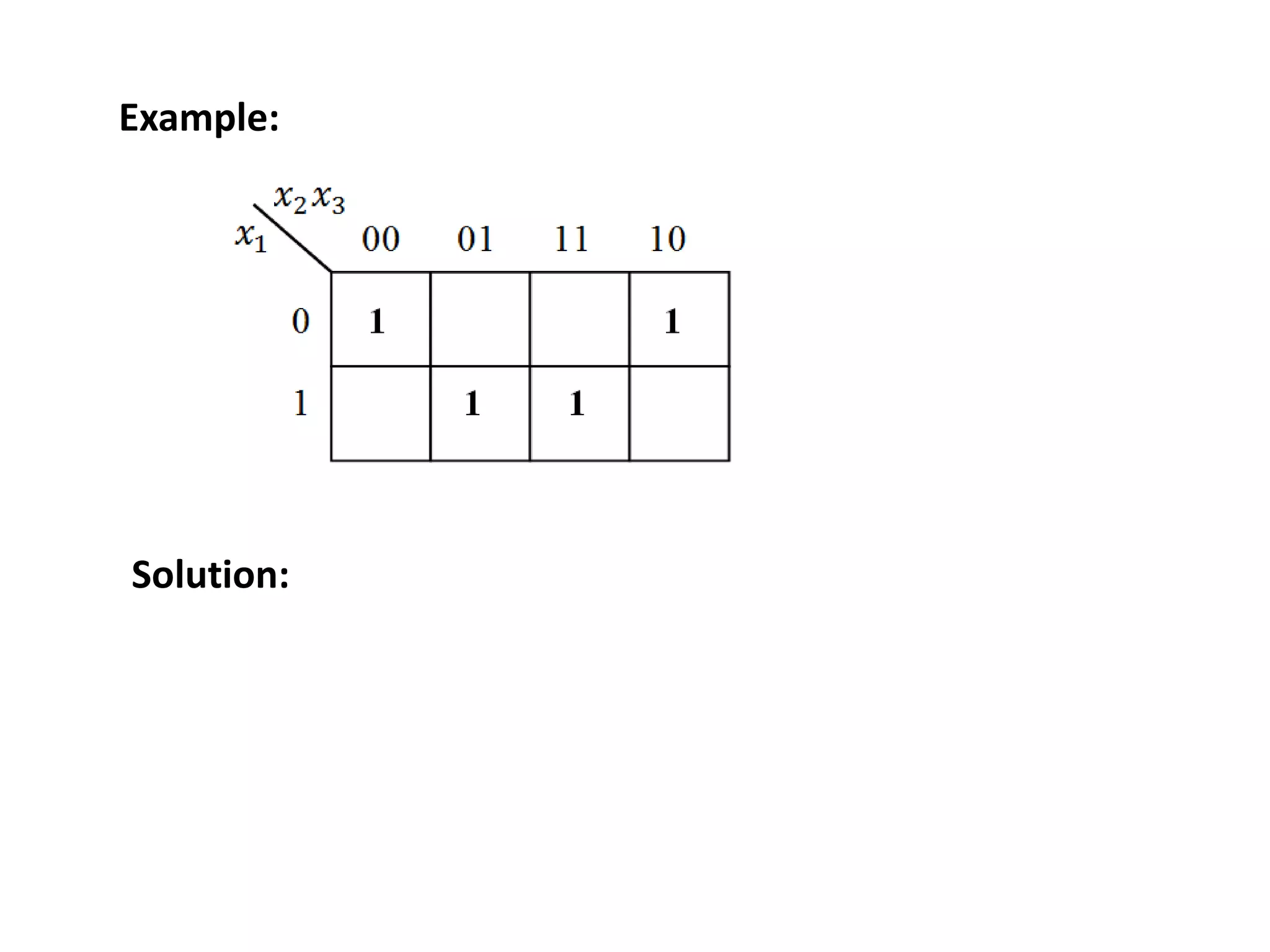
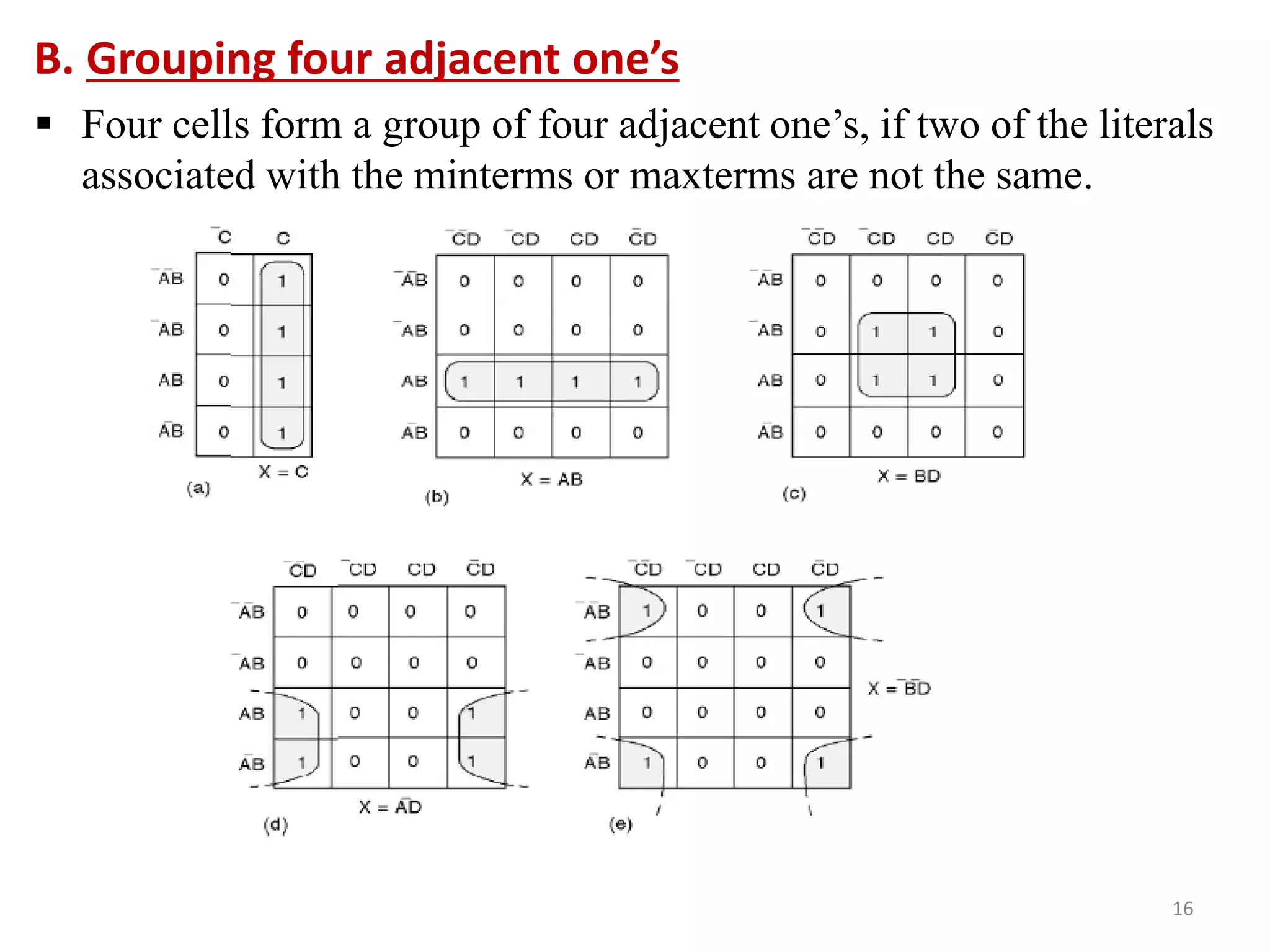
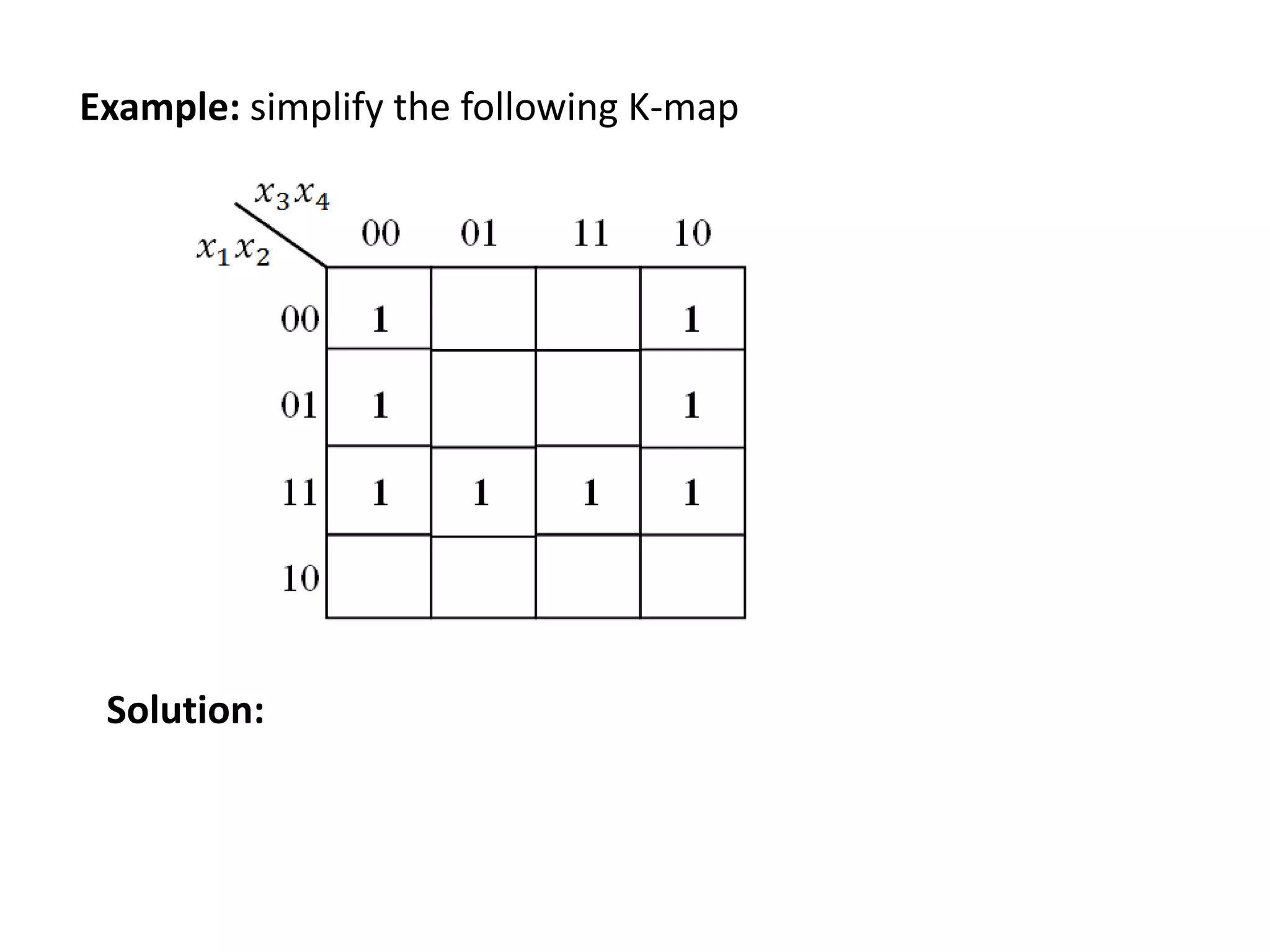
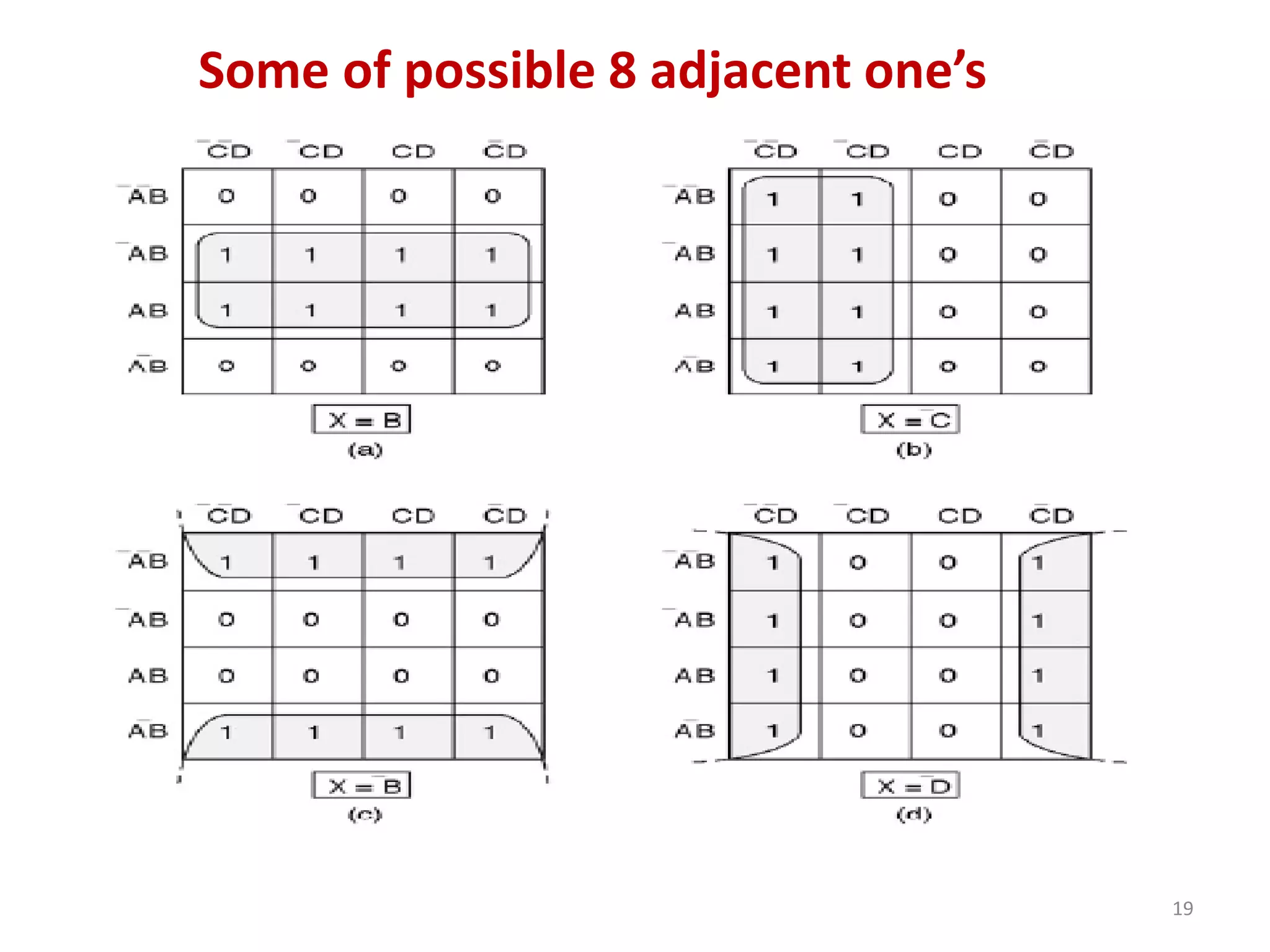
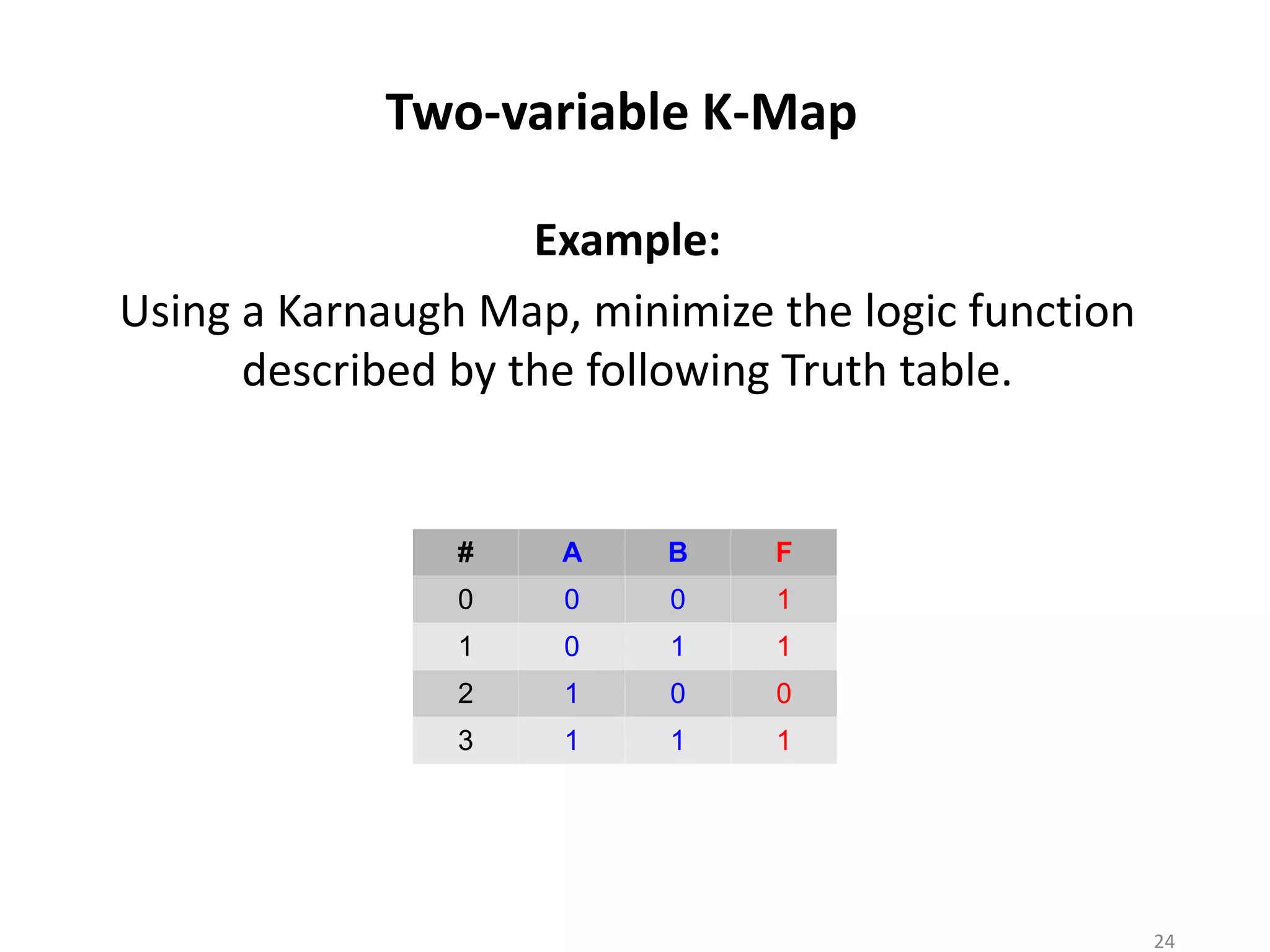
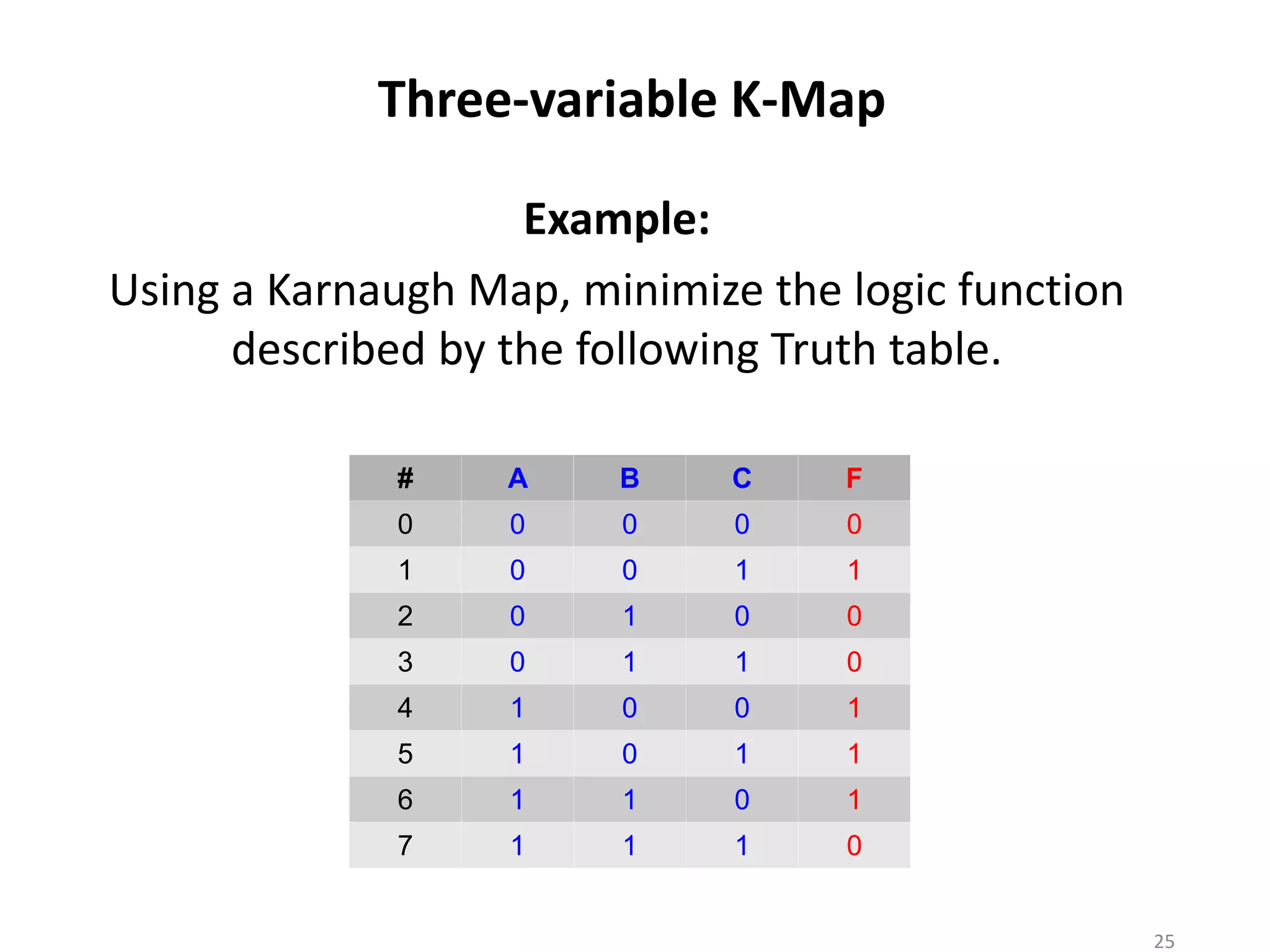
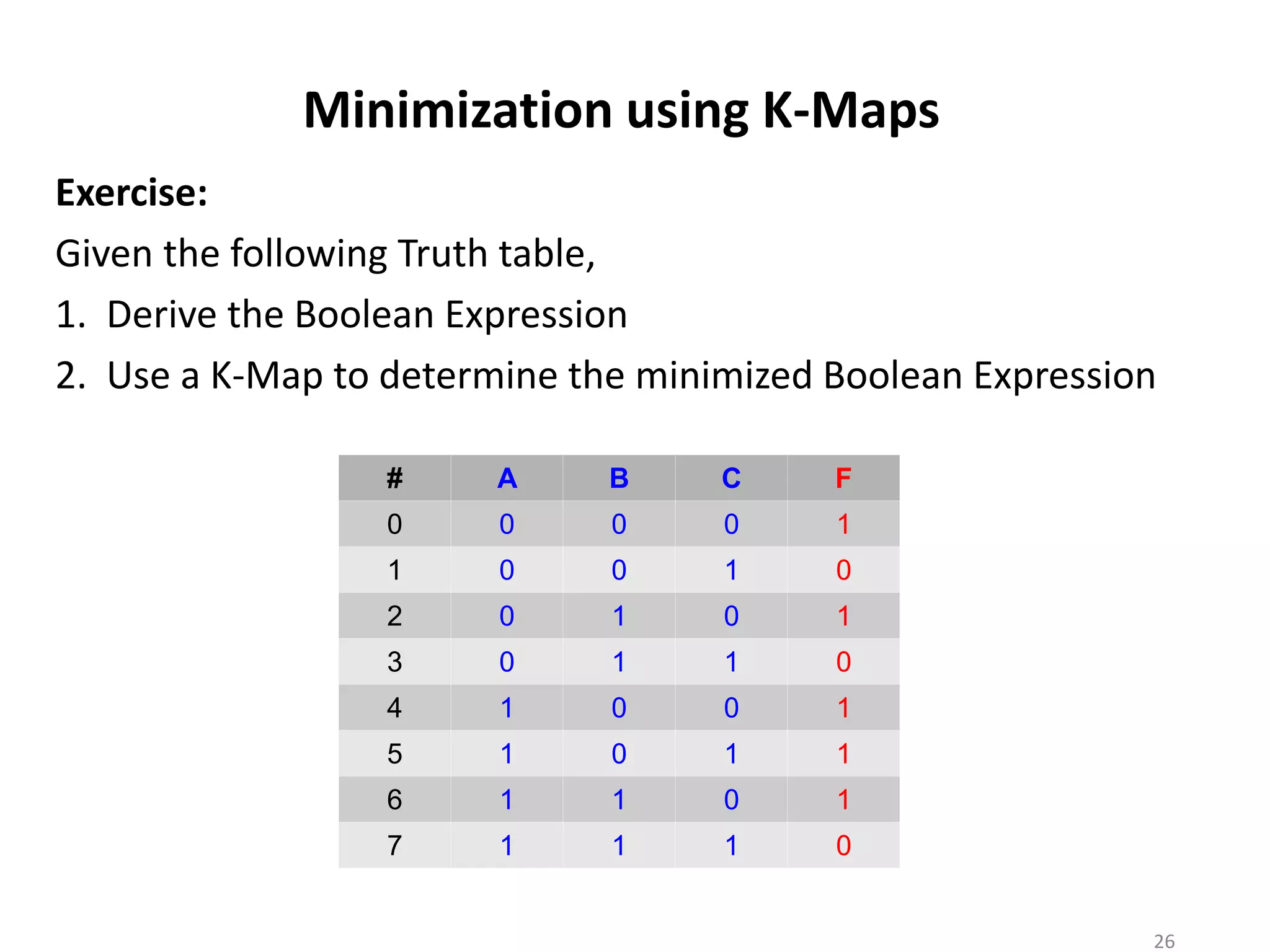
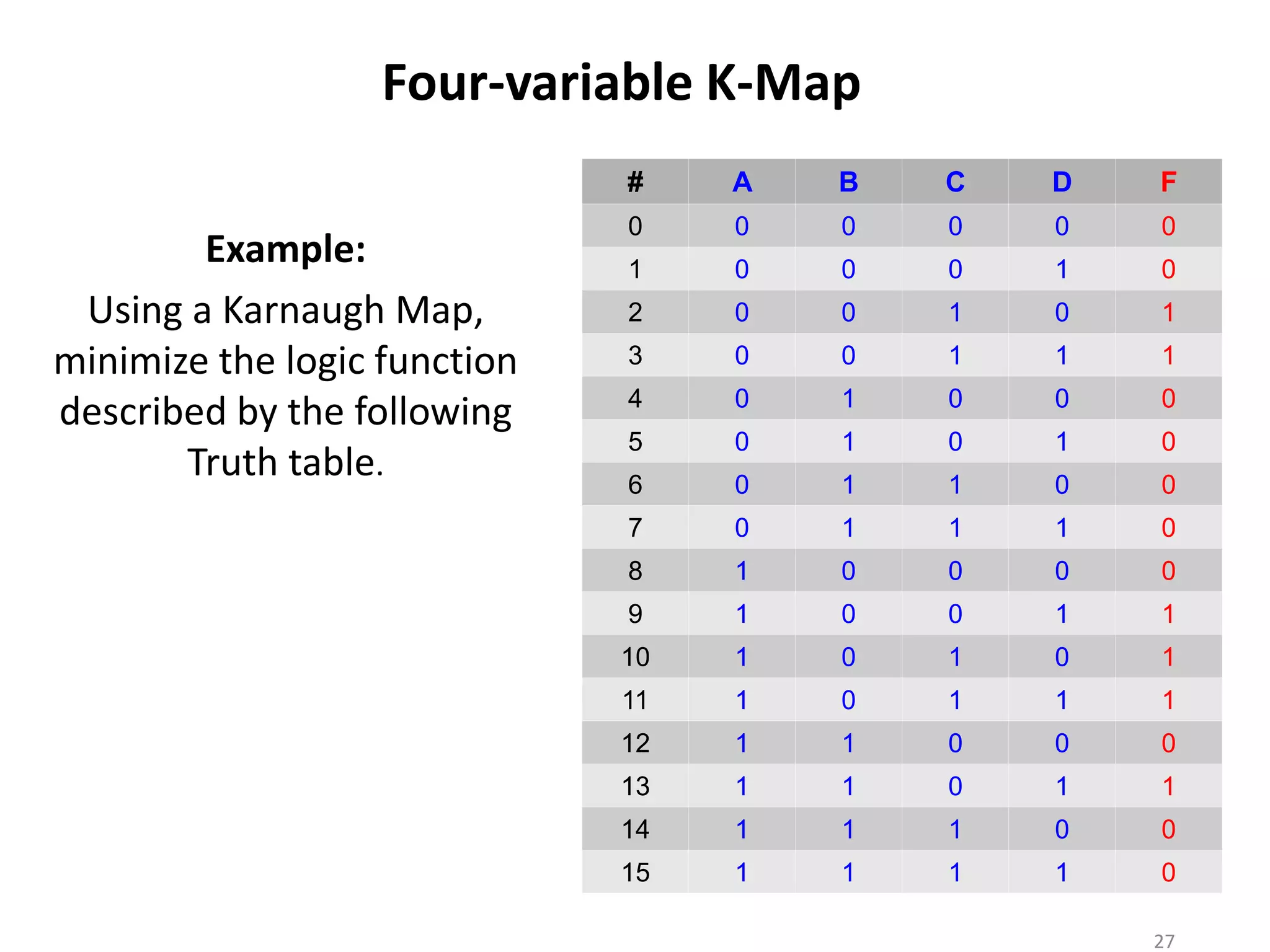
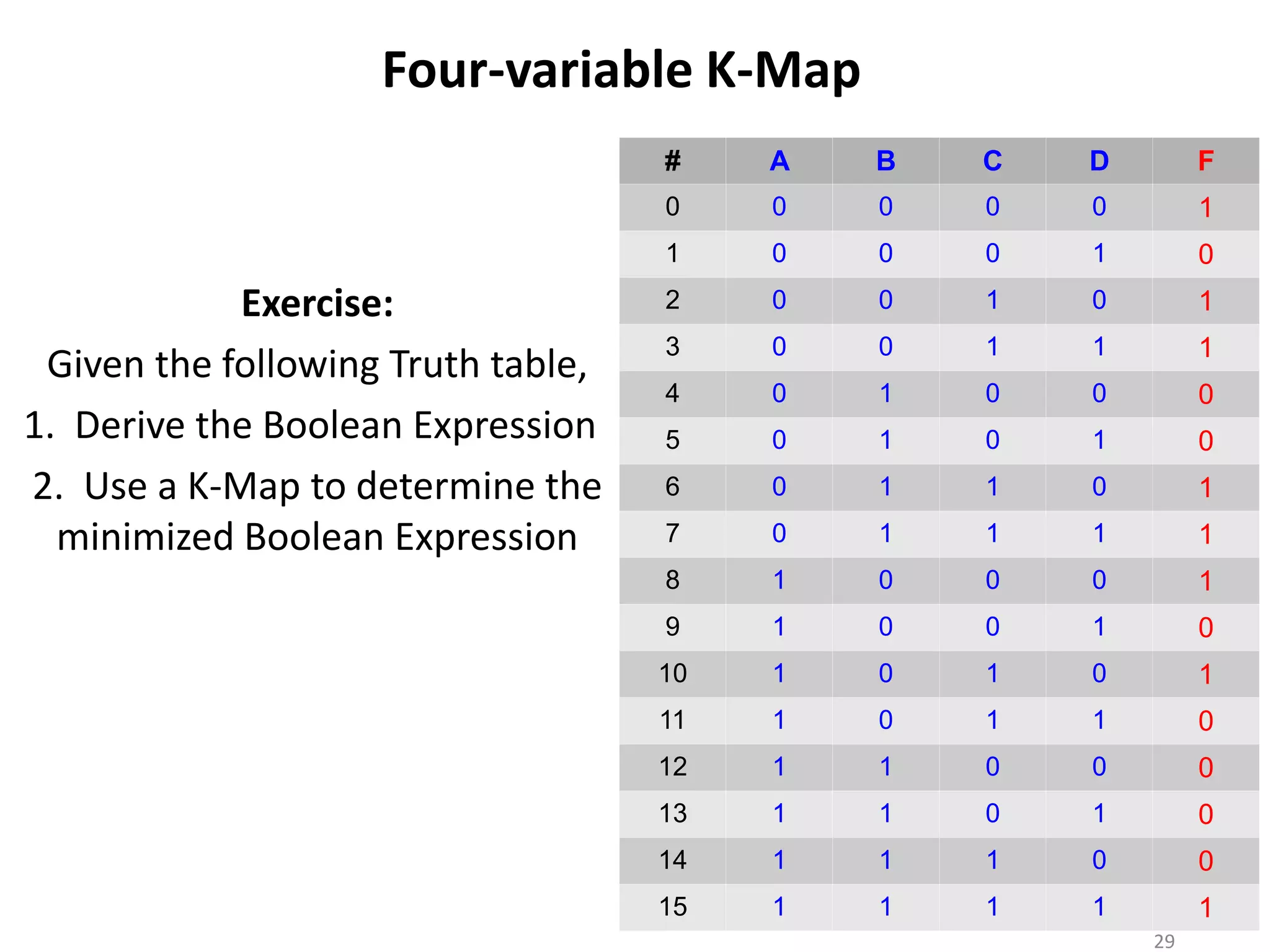
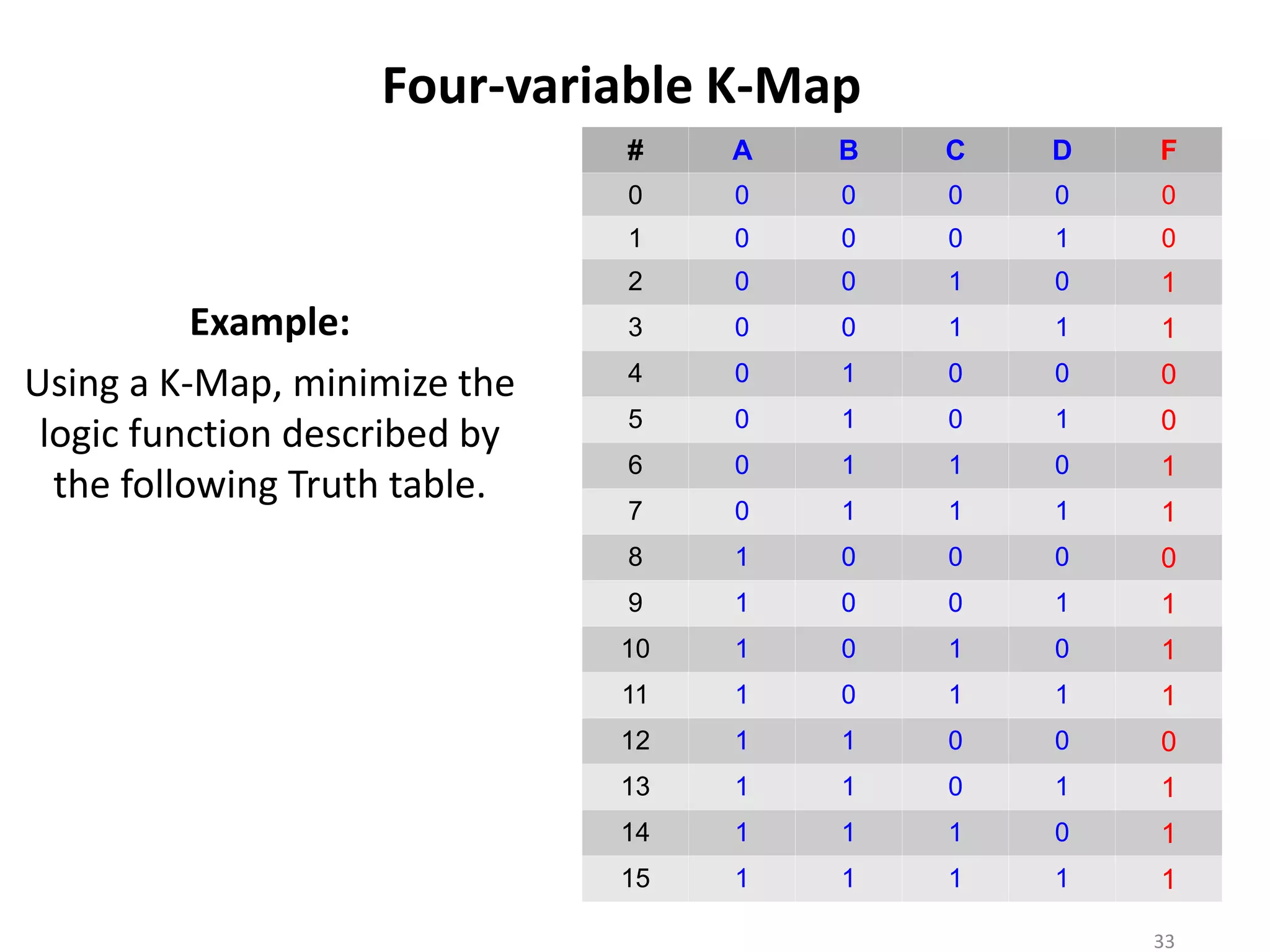
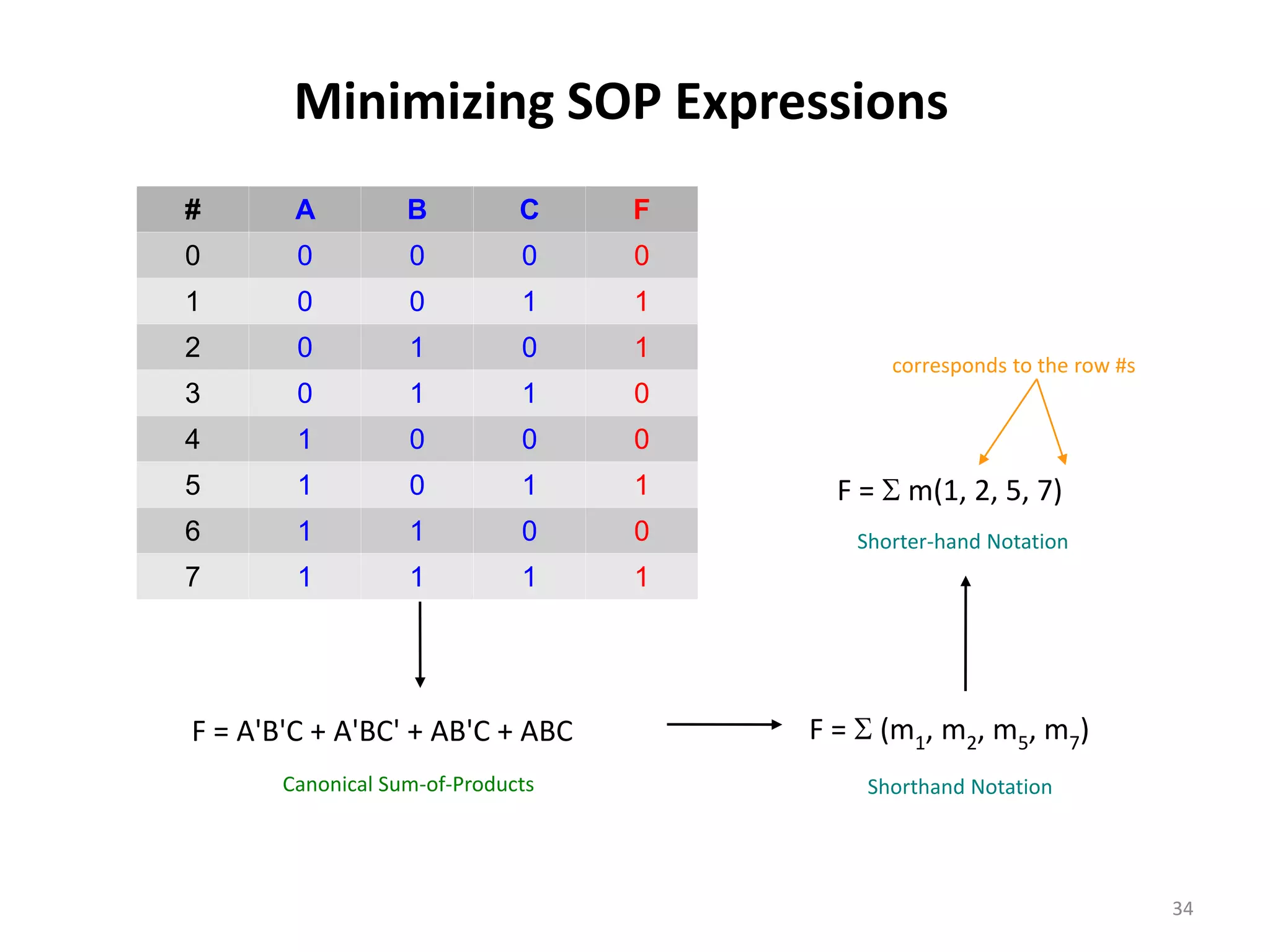
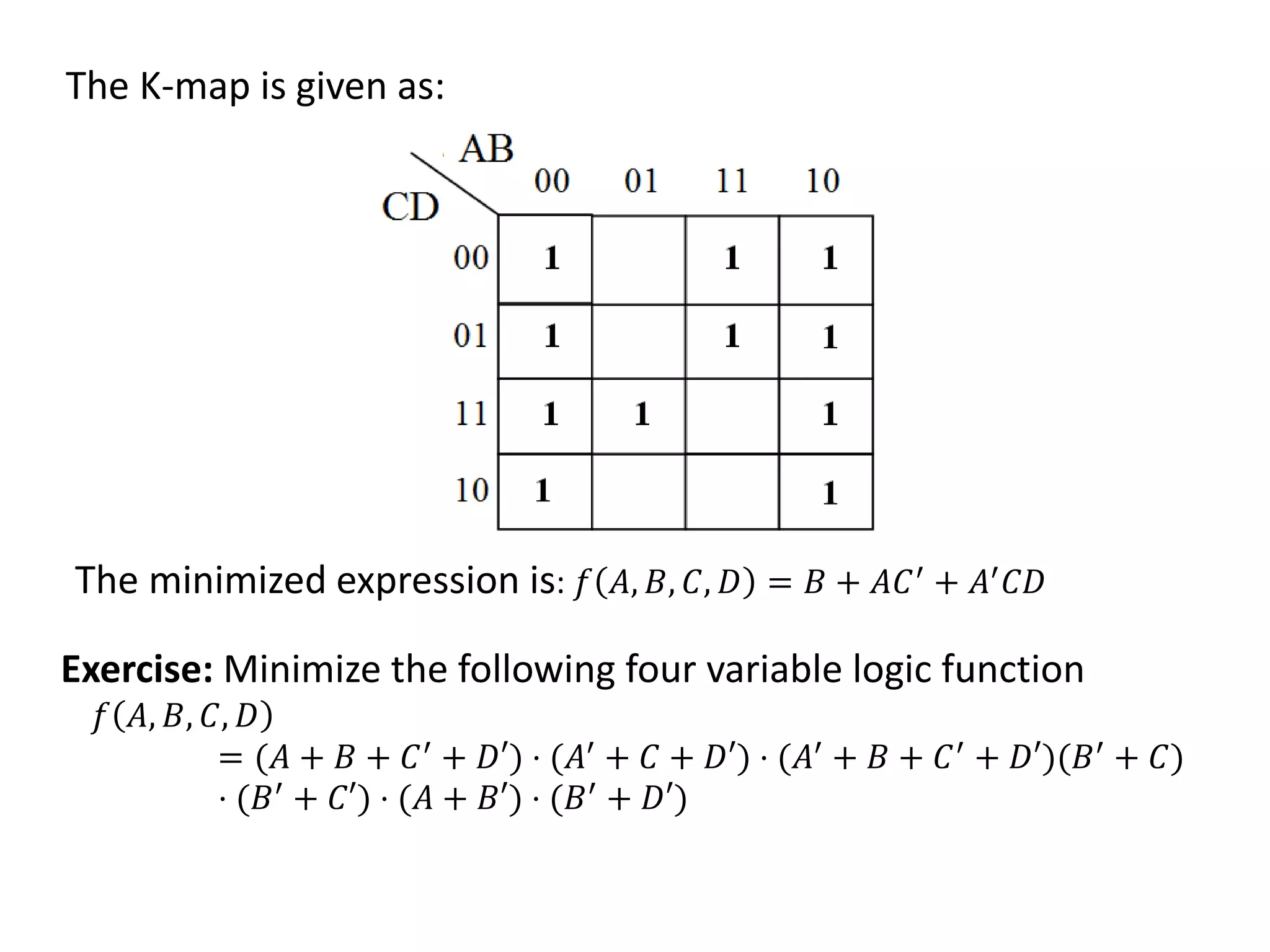
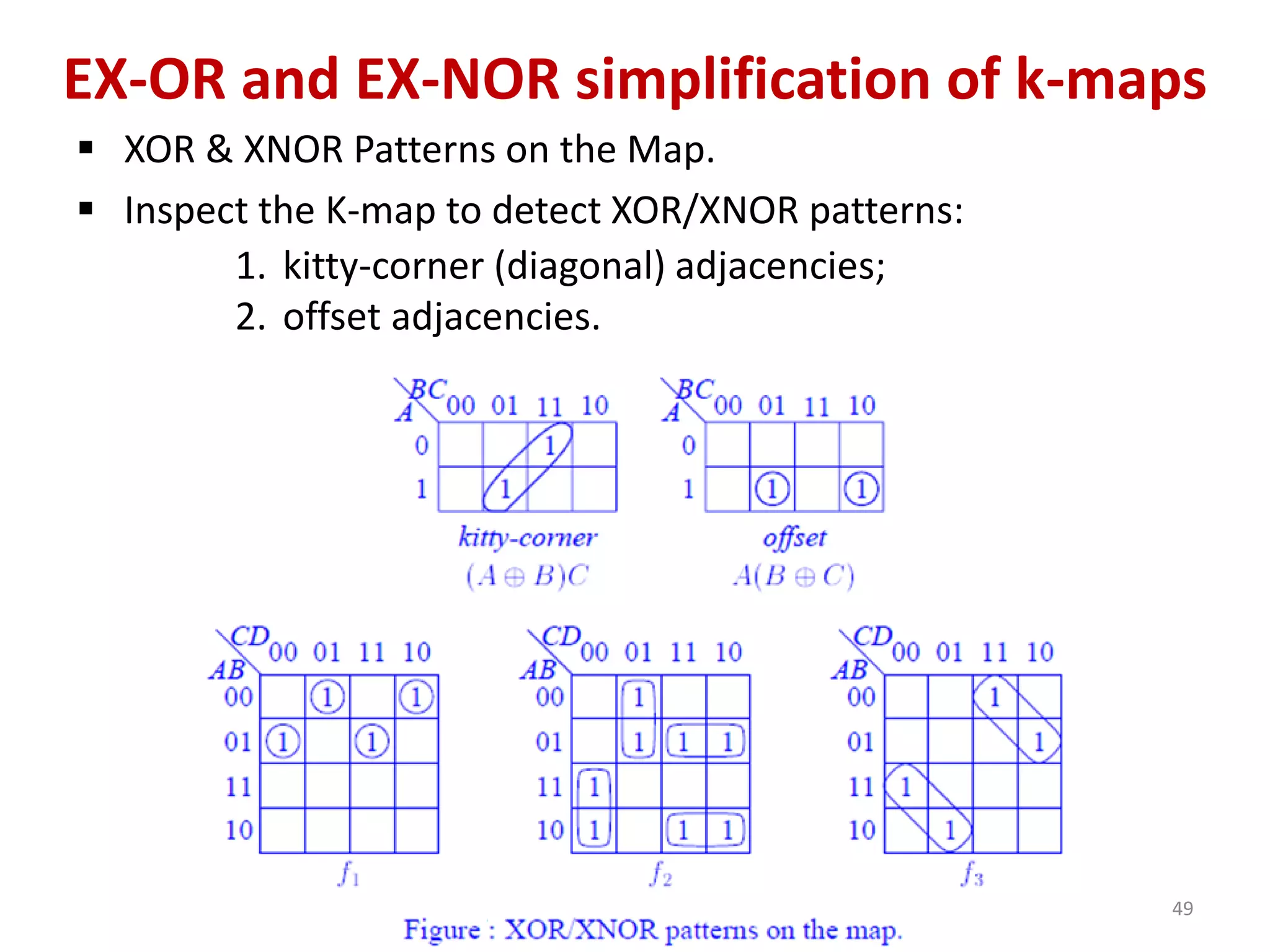
The document discusses techniques for simplifying and minimizing Boolean functions using Karnaugh maps. It covers representing logic functions as K-maps, grouping adjacent 1s and 0s to simplify expressions, and minimizing functions specified as truth tables or minterms/maxterms. Examples are provided to demonstrate minimizing 2, 3, and 4 variable logic functions using K-maps. The document also discusses deriving sum of products and product of sums expressions from K-maps.