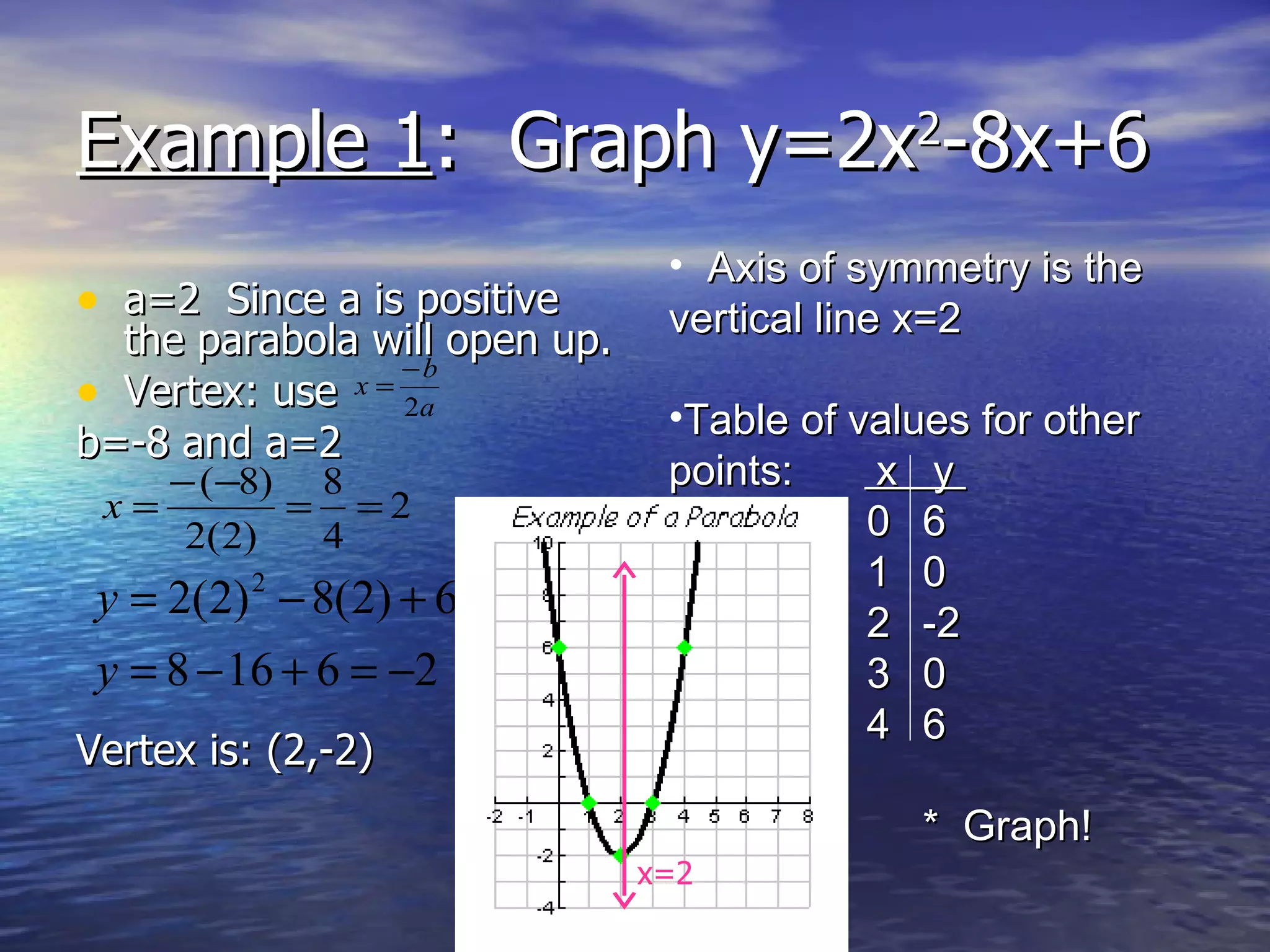
The document discusses graphing quadratic functions. It defines a quadratic function as an equation of the form y=ax^2 +bx+c where a ≠ 0, forming a U-shaped parabola. It explains that the vertex is the highest/lowest point and the axis of symmetry is the vertical line through the vertex. It provides steps for graphing a quadratic function by finding the vertex coordinates using the standard form equation, choosing x-values on each side of the vertex, calculating corresponding y-values, and plotting points connected with a smooth curve. An example problem demonstrates these steps.

1. Graphing Quadratic Functions (Ch 6) Definitions Steps for graphing

2. Quadratic Function A function of the form y=ax 2 +bx+c where a ≠0 making a u-shaped graph called a parabola . Example quadratic equation:

3. Vertex- The lowest or highest point of a parabola. Vertex Axis of symmetry- The vertical line through the vertex of the parabola. Axis of Symmetry

4. Standard Form Equation y=ax 2 + bx + c If a is positive , u opens up If a is negative , u opens down The x-coordinate of the vertex is at To find the y-coordinate of the vertex, plug the x-coordinate into the given eqn. The axis of symmetry is the vertical line x= Choose 2 x-values on either side of the vertex x-coordinate. Use the eqn to find the corresponding y-values. Graph and label the 5 points and axis of symmetry on a coordinate plane. Connect the points with a smooth curve.

5. Example 1 : Graph y=2x 2 -8x+6 a=2 Since a is positive the parabola will open up. Vertex: use b=-8 and a=2 Vertex is: (2,-2) Axis of symmetry is the vertical line x=2 Table of values for other points: x y 0 6 1 0 2 -2 3 0 4 6 * Graph! x=2

6. Now you try one! y=-x 2 +x+12 * Open up or down? * Vertex? * Axis of symmetry? * Table of values with 5 points?

7. (-1,10) (-2,6) (2,10) (3,6) X = .5 (.5,12)

8. Changing from vertex or intercepts form to standard form The key is to use Double Distribution! Ex: y=-(x+4)(x-9) Ex: y=3(x-1) 2 +8 =-(x 2 -9x+4x-36) =3(x-1)(x-1)+8 =-(x 2 -5x-36) =3(x 2 -x-x+1)+8 y=-x 2 +5x+36 =3(x 2 -2x+1)+8 =3x 2 -6x+3+8 y=3x 2 -6x+11