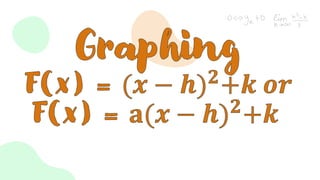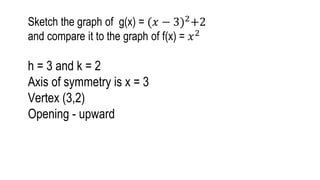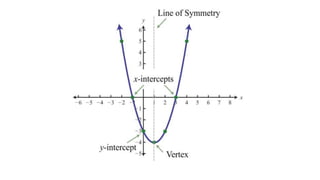
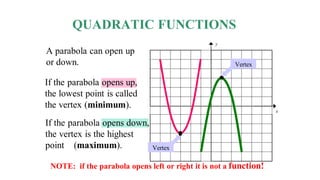
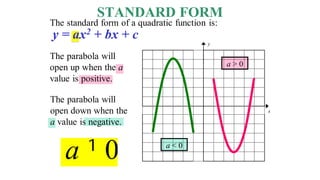
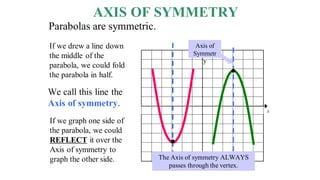
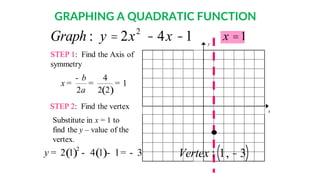
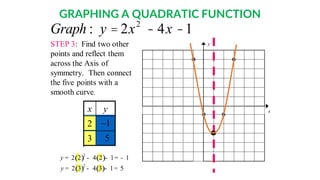
The document discusses key concepts about quadratic functions including: 1) Quadratic functions can be represented by the equation f(x) = ax^2 + bx + c and form a parabolic shape that can open up or down. 2) The axis of symmetry of a parabola passes through the vertex (highest/lowest point) and can be found using the equation x = -b/2a. 3) The vertex coordinates can be determined by substituting the axis of symmetry value into the original equation. 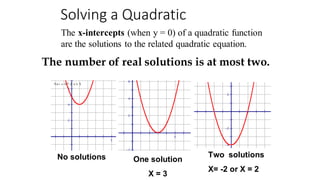4) Quadratic functions can have 0, 1, or 2 x-intercepts depending on the number of real solutions to the related quadratic equation.

4. The picture of the bridge resembles a common graph
with smooth U-shape called a parabola.
f (x) = 𝑎𝑥2
+ bx + c
f (x) = 𝑎 (𝑥 − ℎ)2
+ k

8. QUADRATIC FUNCTIONS
A parabola can open up
or down.
If the parabola opens up,
the lowest point is called
the vertex (minimum).
If the parabola opens down,
the vertex is the highest
point (maximum).
NOTE: if the parabola opens left or right it is not a function!
y
x
Vertex
Vertex

9. y = ax2 + bx + c
The parabola will
open down when the
a value is negative.
The parabola will
open up when the a
value is positive.
STANDARD FORM
y
x
The standard form of a quadratic function is:
a > 0
a < 0
a ¹ 0

11. y
x
Axis of
Symmetr
y
AXIS OF SYMMETRY
Parabolas are symmetric.
If we drew a line down
the middle of the
parabola, we could fold
the parabola in half.
We call this line the
Axis of symmetry.
The Axis of symmetry ALWAYS
passes through the vertex.
If we graph one side of
the parabola, we could
REFLECT it over the
Axis of symmetry to
graph the other side.

12. Find the Axis of symmetry for y = 3x2 – 18x + 7
FINDING THE AXIS OF SYMMETRY
When a quadratic function is in standard form
the equation of the Axis of symmetry is
y = ax2 + bx + c,
2
b
a
x 

 
18
2 3
x 18
6
 3

The Axis of
symmetry
is x = 3.
a = 3 b = -18

14. FINDING THE VERTEX
The Axis of symmetry always goes through the
_______. Thus, the Axis of symmetry gives us
the ____________ of the vertex.
STEP 1: Find the Axis of symmetry
Vertex
Find the vertex of y = -2x2 + 8x - 3
2
b
a
x 
 a = -2 b = 8
x =
-8
2(-2)
=
-8
-4
= 2
X-coordinate
The x-coordinate
of the vertex is 2

15. FINDING THE VERTEX
STEP 1: Find the Axis of symmetry
STEP 2: Substitute the x – value into the original equation
to find the y –coordinate of the vertex.
8 8
2
2 2( 2) 4
b
a
x   
 
 
 
The
vertex is
(2 , 5)
Find the vertex of y = -2x2 + 8x - 3
y = - 2 2
( )
2
+ 8 2
( ) - 3
= - 2 4
( ) +16 - 3
= - 8 +16 - 3
= 5

17. - It is the value of x when y = 0. It is
also called the zero of function.
The graph of a parabola may have
at most two x-intercepts

18. - It is the value of y or f(x) when x = 0.

20. Sketch the graph of g(x) = (𝑥 − 3)2+2
and compare it to the graph of f(x) = 𝑥2
h = 3 and k = 2
Axis of symmetry is x = 3
Vertex (3,2)
Opening - upward

21. TABLE OF VALUES
x
0 11
1 6
2 3
3 2
4 3
5 6
6 11

23. GRAPHING A QUADRATIC FUNCTION
There are 3 steps to graphing a parabola in
standard form.
STEP 1: Find the Axis of symmetry using:
STEP 2: Find the vertex
STEP 3: Find two other points and reflect them
across the Axis of symmetry. Then connect the five
points with a smooth curve.
MAKE A TABLE
using x – values close to
the Axis of symmetry.
2
b
a
x 


24. STEP 1: Find the Axis of
symmetry
( )
4
1
2 2 2
b
x
a
-
= = =
y
x
Graph : y = 2x2
- 4x -1
GRAPHING A QUADRATIC FUNCTION
STEP 2: Find the vertex
Substitute in x = 1 to
find the y – value of the
vertex.
( ) ( )
2
2 1 4 1 1 3
y = - - = - Vertex : 1, - 3
( )
x =1

25. 5
–1
( ) ( )
2
2 3 4 3 1 5
y = - - =
STEP 3: Find two other
points and reflect them
across the Axis of
symmetry. Then connect
the five points with a
smooth curve.
y
x
( ) ( )
2
2 2 4 2 1 1
y = - - = -
3
2
y
x
GRAPHING A QUADRATIC FUNCTION
Graph : y = 2x2
- 4x -1

26. Y-INTERCEPT OF A QUADRATIC FUNCTION
y = 2x2
- 4x -1 Y-axis
The y-intercept of a
Quadratic function can
Be found when x = 0.
y = 2x2
- 4x -1
= 2 0
( )2
- 4(0) -1
= 0 - 0 -1
= -1
The constant term is always the y- intercept

27. y
x

28. Solving a Quadratic
The number of real solutions is at most two.
No solutions One solution
X = 3
Two solutions
X= -2 or X = 2
The x-intercepts (when y = 0) of a quadratic function
are the solutions to the related quadratic equation.