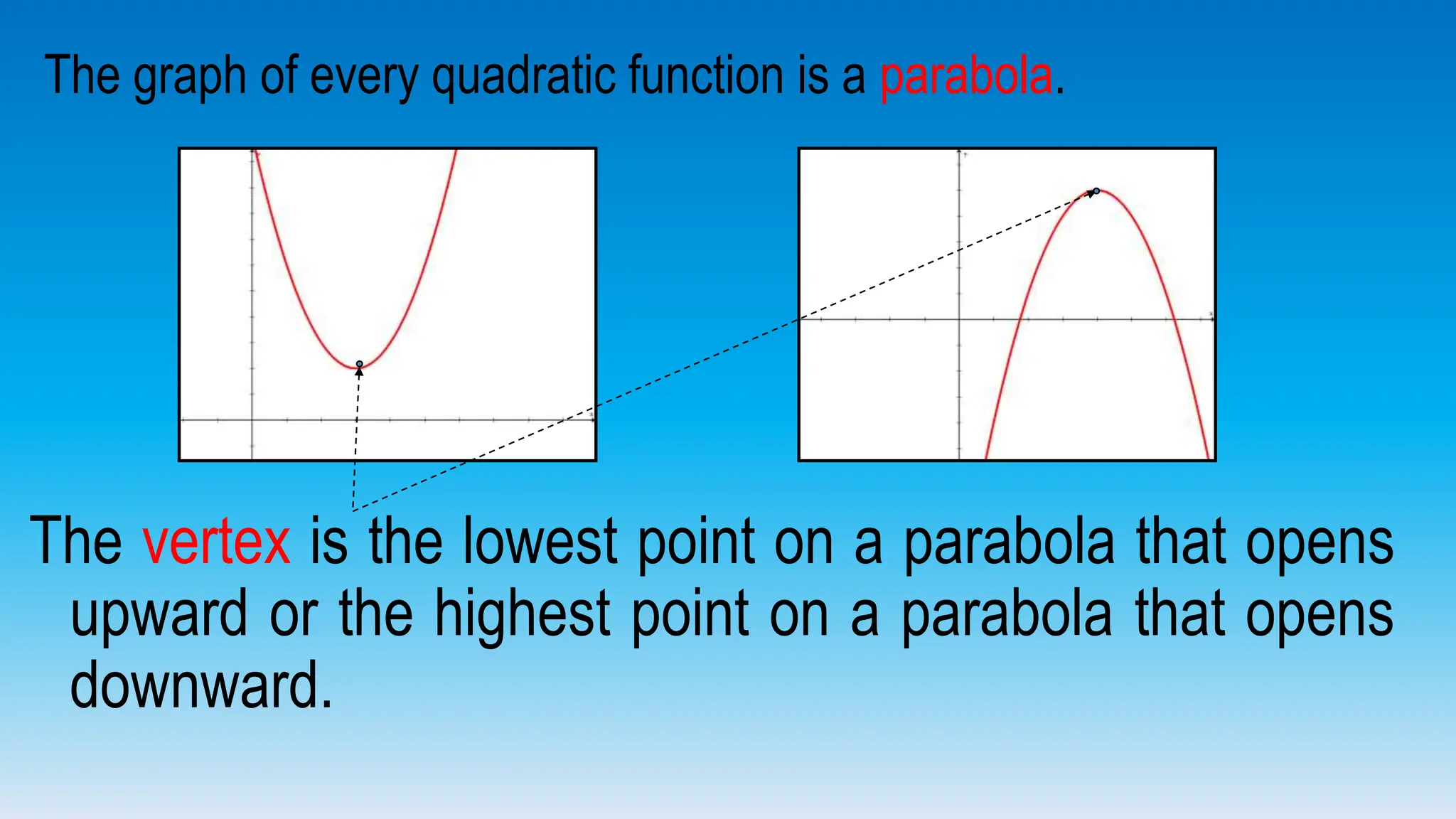
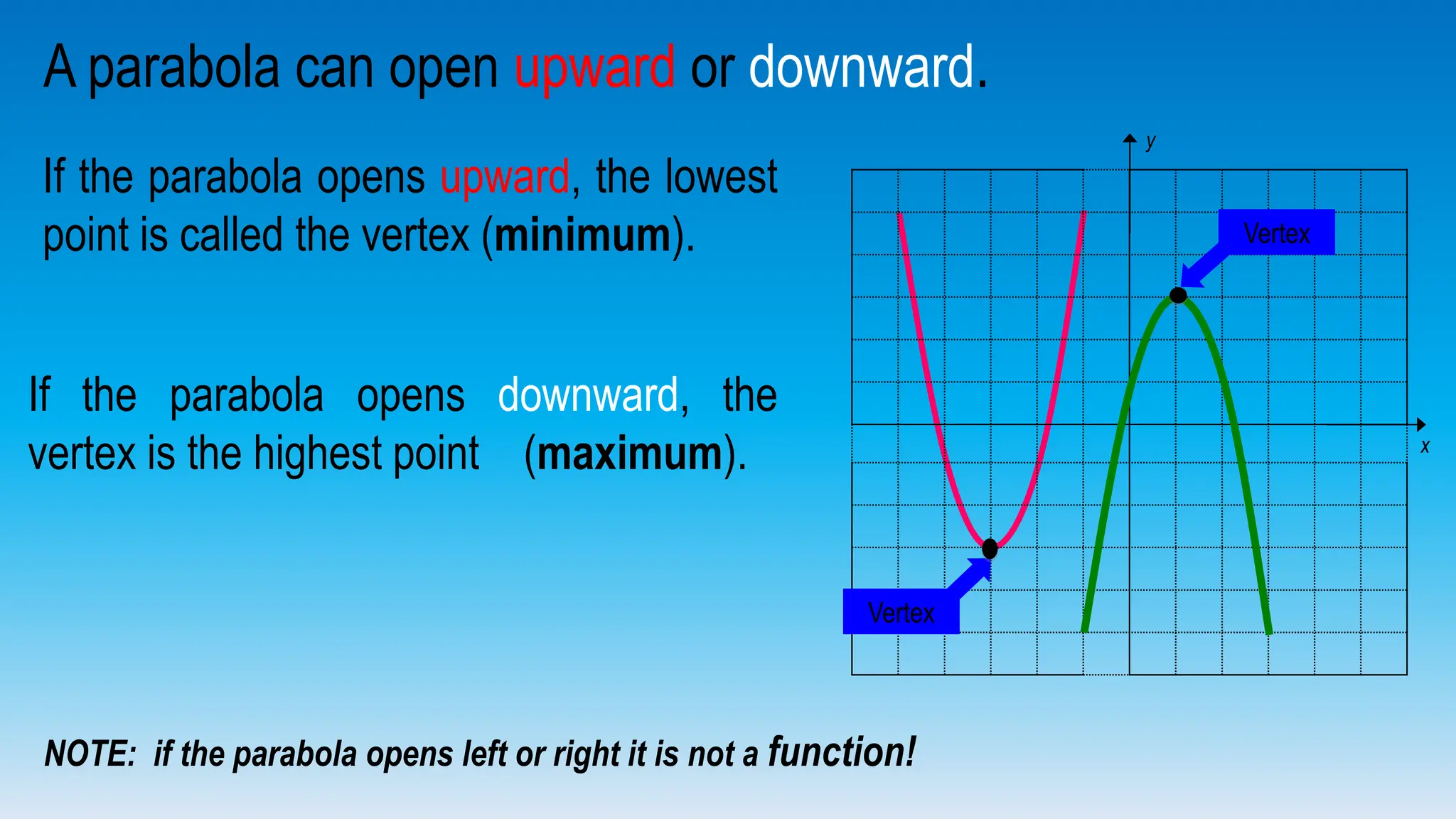
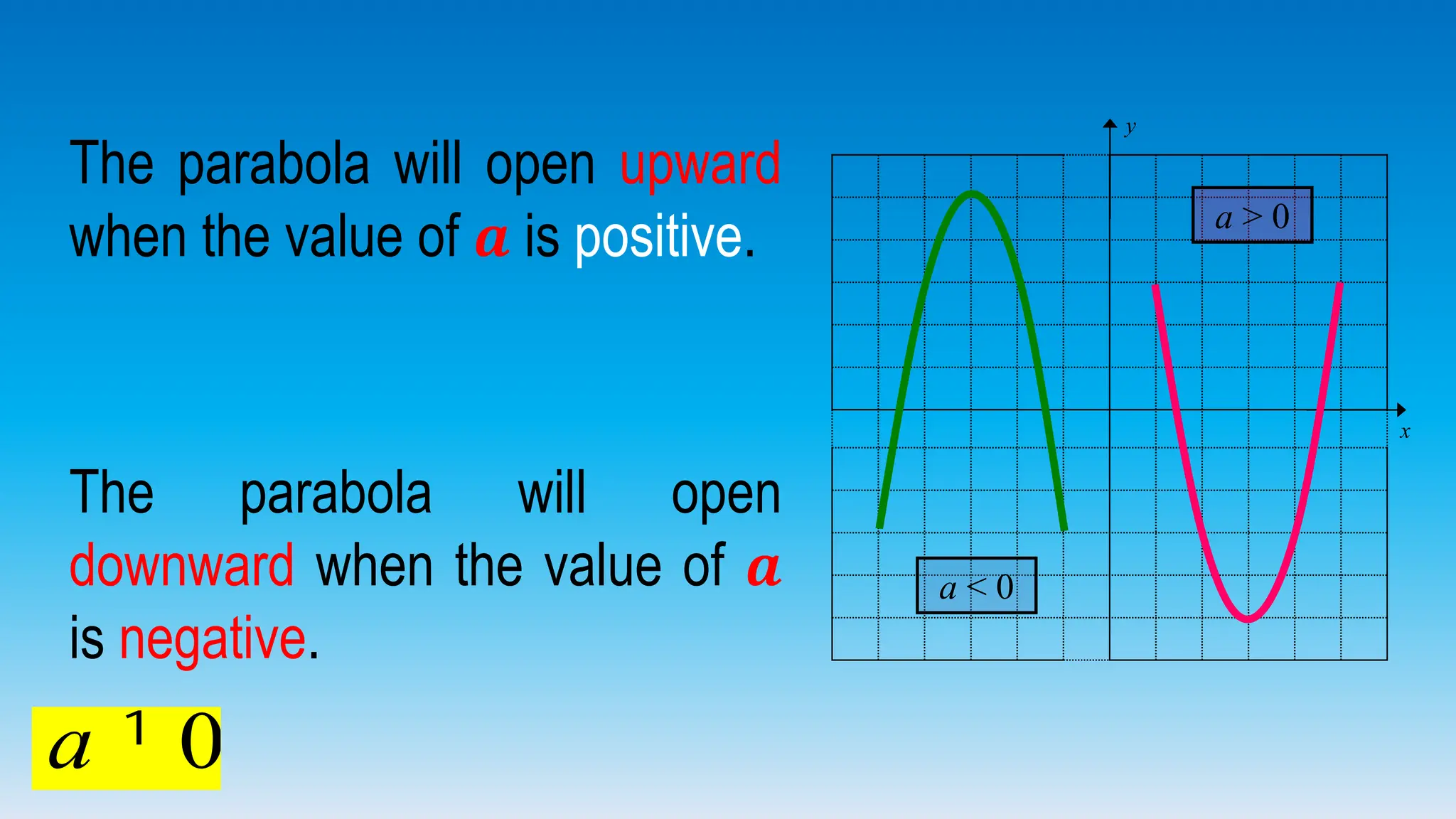
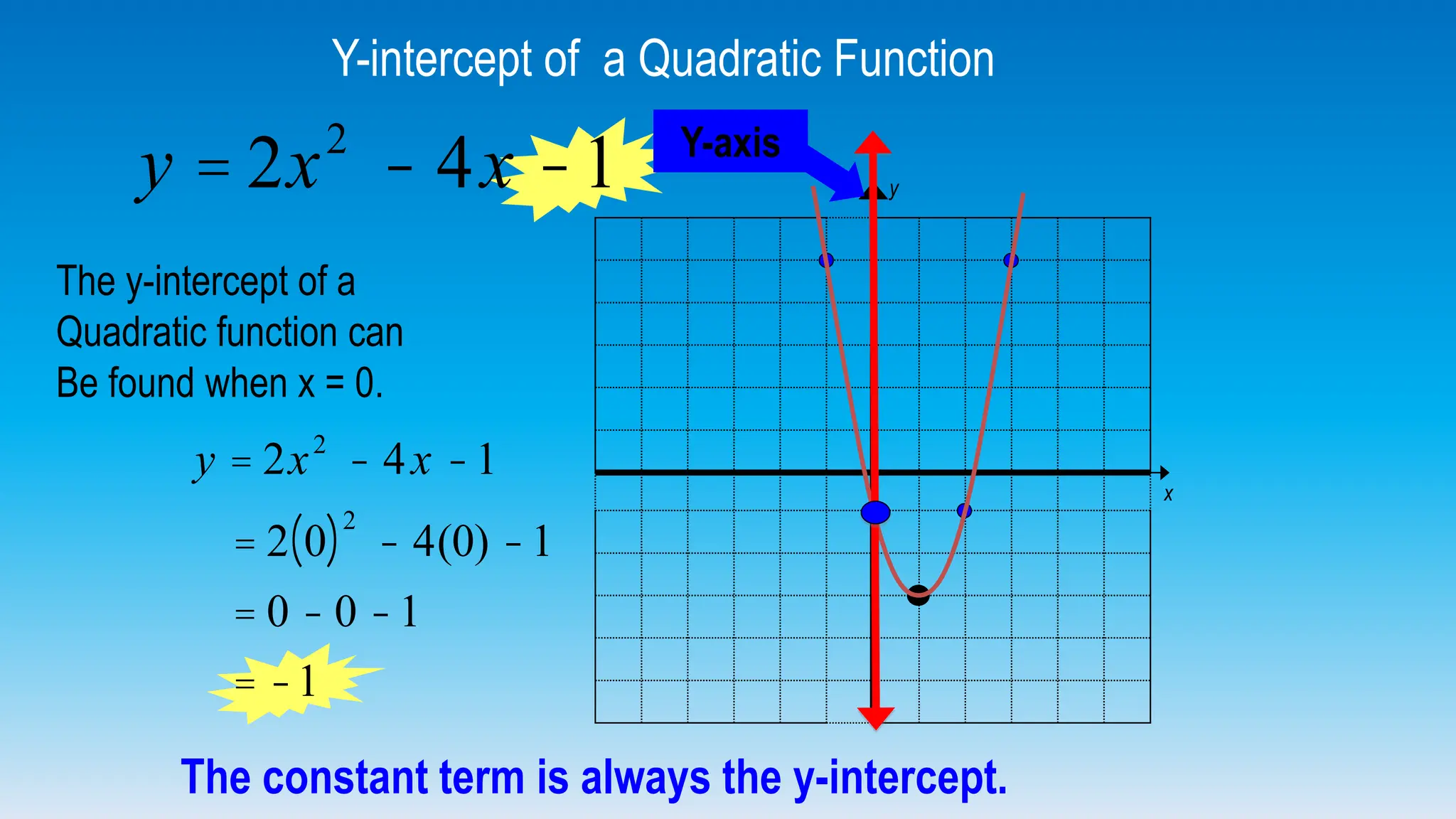
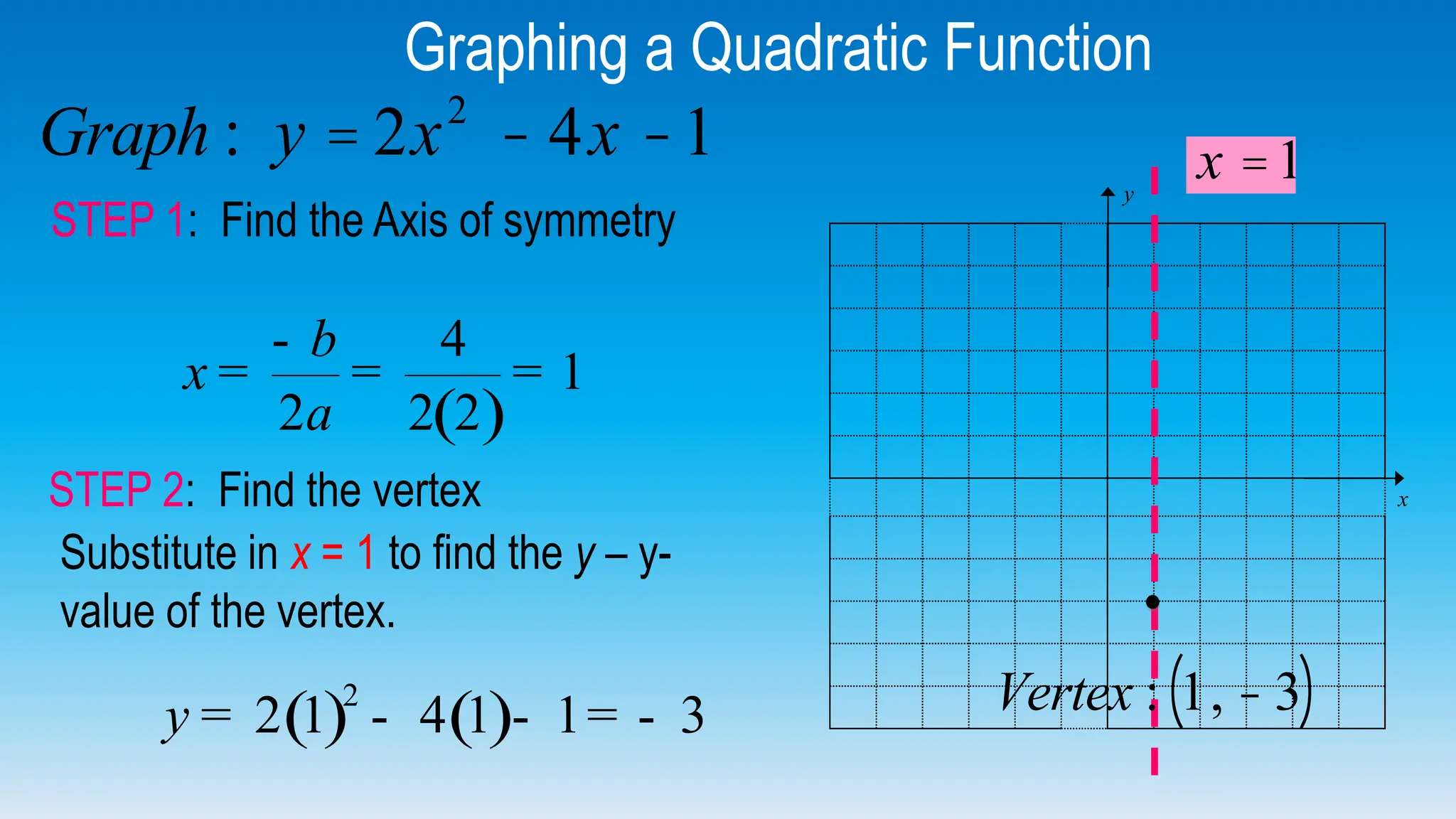
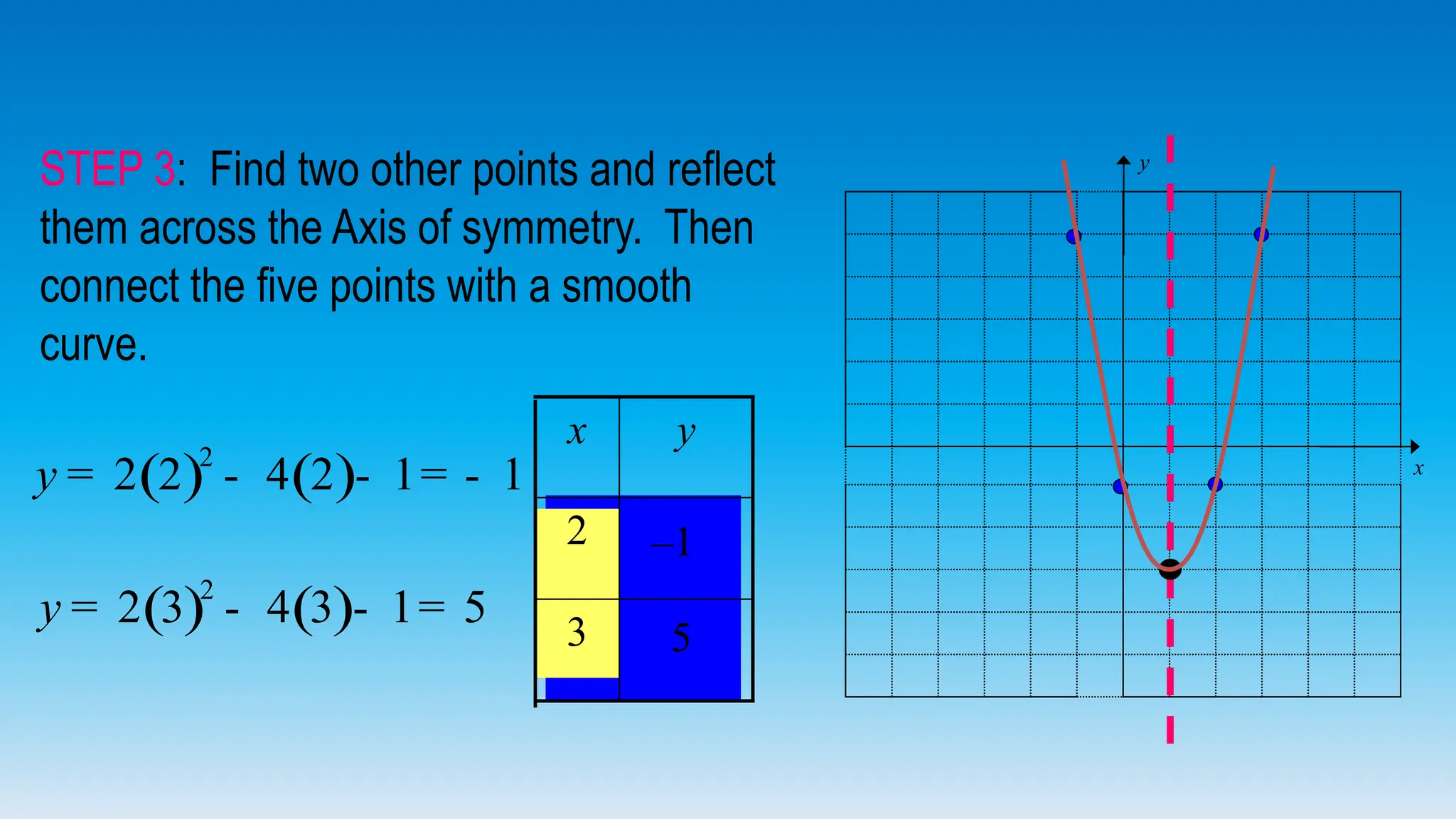
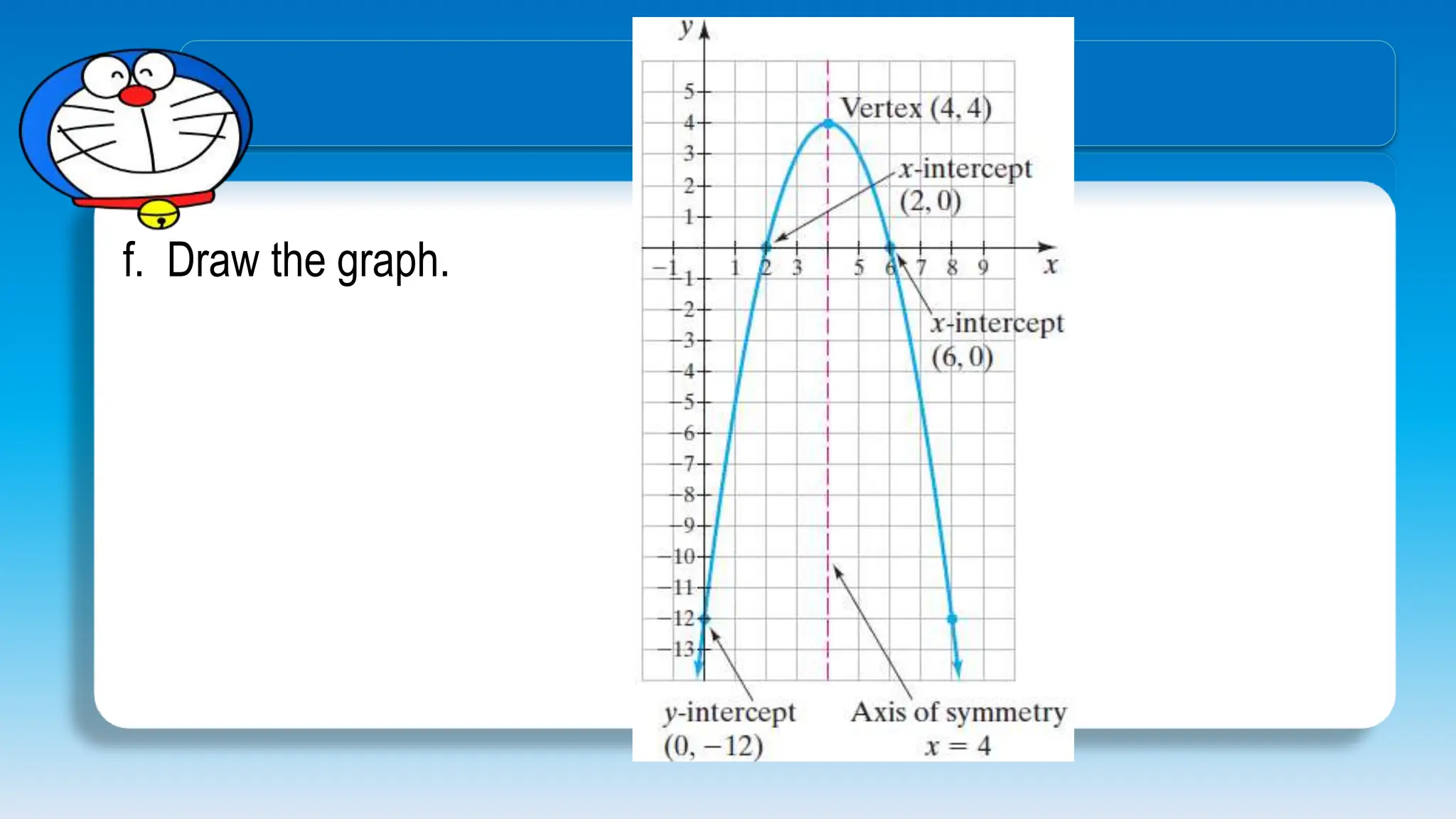
The document explains how to graph quadratic functions, including determining the domain, range, intercepts, axis of symmetry, and vertex. It defines a quadratic function in the form f(x) = ax² + bx + c, discusses the characteristics of parabolas, and provides step-by-step examples of graphing techniques. The document emphasizes the role of the coefficient 'a' in determining the direction in which the parabola opens and how to find critical points on the graph.

2. OBJECTIVES
Draw the graphs of a quadratic function.
Determine and identify the domain, range,
intercepts, axis of symmetry, and the opening
of the parabola.
Show appreciation of the graph of quadratic
function through active participation in classroom
activities

4. Graphing
Quadratic
Functions

5. Quadratic Function
A quadratic function is a function that can
be written in the form
f(x) = ax2 + bx + c
For real numbers a, b, and c, with a ≠ 0.

6. The graph of every quadratic function is a parabola.
The vertex is the lowest point on a parabola that opens
upward or the highest point on a parabola that opens
downward.

7. A parabola can open upward or downward.
If the parabola opens upward, the lowest
point is called the vertex (minimum).
If the parabola opens downward, the
vertex is the highest point (maximum).
NOTE: if the parabola opens left or right it is not a function!
y
x
Vertex
Vertex

8. The parabola will open
downward when the value of 𝒂
is negative.
The parabola will open upward
when the value of 𝒂 is positive.
y
x
a > 0
a < 0
a ¹ 0

9. Graphs of quadratic equations have symmetry about a line
through the vertex. This line is called the axis of symmetry.
The sign of a, the numerical coefficient of the squared term,
determines whether the parabola will open upward or
downward.

10. Vertex of a Parabola
The parabola represented by the function f(x) = ax2 + bx + c will have
vertex
Since we often find the y-coordinate of the vertex by substituting the x-
coordinate of the vertex into f(x), the vertex may also be designated as





 

a
b
ac
a
b
4
4
,
2
2













a
b
f
a
b
2
,
2

11. Axis of Symmetry
For a quadratic function of the form f(x) = ax2 + bx +
c, the equation of the axis of symmetry of the
parabola is
a
b
x
2



12. x-Intercepts of a Parabola
To find the x-intercepts (if there are any) of a quadratic
function, solve the equation ax2 + bx + c = 0 for x.
This equation may be solved by factoring, by using the
quadratic formula, or by completing the square.

13. y
x
Y-intercept of a Quadratic Function
y = 2x2
- 4x -1 Y-axis
The y-intercept of a
Quadratic function can
Be found when x = 0.
y = 2x2
- 4x -1
= 2 0
( )2
- 4(0) -1
= 0 - 0 -1
= -1
The constant term is always the y-intercept.

14. STEP 1: Find the Axis of symmetry
( )
4
1
2 2 2
b
x
a
-
= = =
y
x
Graph : y = 2x2
- 4x -1
Graphing a Quadratic Function
STEP 2: Find the vertex
Substitute in x = 1 to find the y – y-
value of the vertex.
( ) ( )
2
2 1 4 1 1 3
y = - - = - Vertex : 1, - 3
( )
x =1

15. 5
–1
( ) ( )
2
2 3 4 3 1 5
y = - - =
STEP 3: Find two other points and reflect
them across the Axis of symmetry. Then
connect the five points with a smooth
curve.
y
x
( ) ( )
2
2 2 4 2 1 1
y = - - = -
3
2
y
x

16. Example Consider the quadratic function
y = -x2 + 8x – 12.
a. Determine whether the parabola opens upward or downward.
b. Find the y-intercept.
c. Find the vertex.
d. Find the axis of symmetry.
e. Find the x-intercepts, if any.
f. Draw the graph.

17. a. Since a is -1, which is less than 0, the parabola opens downward.
b. To find the y-intercept, set x = 0 and solve for y.
12
12
)
0
(
8
)
0
( 2






y
The y-intercept is (0, 12)
Example Consider the quadratic function
y = -x2 + 8x – 12.

18. c. First, find the x-coordinate, then find the y-coordinate of the vertex. From the
function, a = -1, b = 8, and c = -12.
continued
4
)
1
(
2
8
2





a
b
x
Since the x-coordinate of the vertex is not a fraction, we will substitute x = 4 into the
original function to determine the y-coordinate of the vertex.
4
12
32
16
12
)
4
(
8
)
4
(
12
8
2
2













y
x
x
y
The vertex is (4, 4).

19. d. Since the axis of symmetry is a vertical line through
the vertex, the equation is found using the same formula
used to find the x-coordinate of the vertex. Thus, the
equation of the axis of symmetry is x = 4.

20. e. To find the x-intercepts, set y = 0.
2
x
6
0
2
or
0
6
0
)
2
)(
6
(
0
12
8
2












x
x
x
x
x
x
x
Thus, the x-intercepts are (2, 0) and (6, 0). These values could also be
found by the quadratic formula (or by completing the square).

21. f. Draw the graph.