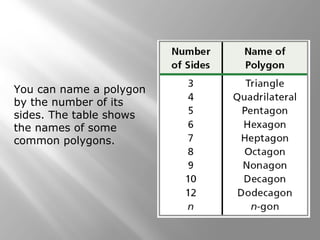
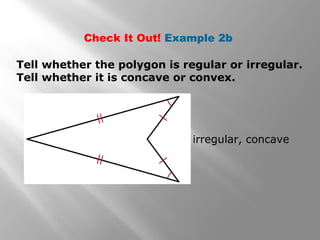
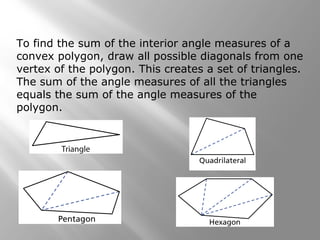
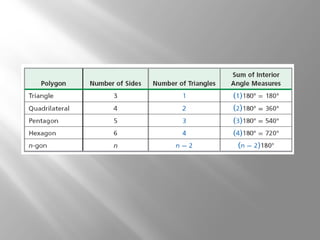
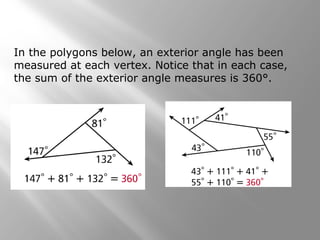
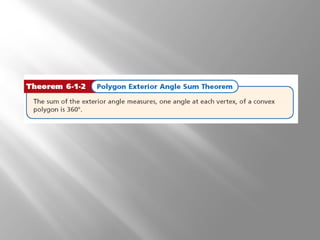
This document provides an overview of polygons and their properties. It begins with objectives and vocabulary related to polygons, such as sides, vertices, diagonals, regular polygons, and convex vs concave shapes. Examples are provided to classify polygons based on their number of sides and whether they are regular, irregular, convex, or concave. The document also discusses finding the sum of interior and exterior angle measures in polygons using theorems. Lesson examples calculate sums and individual angle measures in various polygons.

1. Holt Geometry
UUNNIITT 66..11 PPOOLLYYGGOONNSS

2. Warm Up
1. A ? is a three-sided polygon.
2. A ? is a four-sided polygon.
Evaluate each expression for n = 6.
3. (n – 4) 12
4. (n – 3) 90
Solve for a.
5. 12a + 4a + 9a = 100
triangle
quadrilateral
24
270
4

3. Objectives
Classify polygons based on their sides
and angles.
Find and use the measures of interior
and exterior angles of polygons.

4. Vocabulary
side of a polygon
vertex of a polygon
diagonal
regular polygon
concave
convex

5. Each segment that forms a polygon is a side of
the polygon. The common endpoint of two sides
is a vertex of the polygon. A segment that
connects any two nonconsecutive vertices is a
diagonal.

6. You can name a polygon
by the number of its
sides. The table shows
the names of some
common polygons.

7. Remember!
A polygon is a closed plane figure formed by
three or more segments that intersect only at
their endpoints.

8. Example 1A: Identifying Polygons
Tell whether the figure is a polygon. If it is a
polygon, name it by the number of sides.
polygon, hexagon

9. Example 1B: Identifying Polygons
Tell whether the figure is a polygon. If it is a
polygon, name it by the number of sides.
polygon, heptagon

10. Example 1C: Identifying Polygons
Tell whether the figure is a polygon. If it is a
polygon, name it by the number of sides.
not a polygon

11. Check It Out! Example 1a
Tell whether each figure is a polygon. If it is a
polygon, name it by the number of its sides.
not a polygon

12. Check It Out! Example 1b
Tell whether the figure is a polygon. If it is a
polygon, name it by the number of its sides.
polygon, nonagon

13. Check It Out! Example 1c
Tell whether the figure is a polygon. If it is a
polygon, name it by the number of its sides.
not a polygon

14. All the sides are congruent in an equilateral polygon.
All the angles are congruent in an equiangular
polygon. A regular polygon is one that is both
equilateral and equiangular. If a polygon is not
regular, it is called irregular.

15. A polygon is concave if any part of a diagonal
contains points in the exterior of the polygon. If no
diagonal contains points in the exterior, then the
polygon is convex. A regular polygon is always
convex.

16. Example 2A: Classifying Polygons
Tell whether the polygon is regular or irregular.
Tell whether it is concave or convex.
irregular, convex

17. Example 2B: Classifying Polygons
Tell whether the polygon is regular or irregular.
Tell whether it is concave or convex.
irregular, concave

18. Example 2C: Classifying Polygons
Tell whether the polygon is regular or irregular.
Tell whether it is concave or convex.
regular, convex

19. Check It Out! Example 2a
Tell whether the polygon is regular or irregular.
Tell whether it is concave or convex.
regular, convex

20. Check It Out! Example 2b
Tell whether the polygon is regular or irregular.
Tell whether it is concave or convex.
irregular, concave

21. To find the sum of the interior angle measures of a
convex polygon, draw all possible diagonals from one
vertex of the polygon. This creates a set of triangles.
The sum of the angle measures of all the triangles
equals the sum of the angle measures of the
polygon.

22. Remember!
By the Triangle Sum Theorem, the sum of the
interior angle measures of a triangle is 180°.

24. In each convex polygon, the number of triangles
formed is two less than the number of sides n. So
the sum of the angle measures of all these triangles
is (n — 2)180°.

25. Example 3A: Finding Interior Angle Measures and
Sums in Polygons
Find the sum of the interior angle measures of a
convex heptagon.
(n – 2)180°
(7 – 2)180°
900°
Polygon Ð Sum Thm.
A heptagon has 7 sides,
so substitute 7 for n.
Simplify.

26. Example 3B: Finding Interior Angle Measures and
Sums in Polygons
Find the measure of each interior angle of a
regular 16-gon.
Step 1 Find the sum of the interior angle measures.
Polygon Ð Sum Thm.
(n – 2)180°
(16 – 2)180° = 2520°
Substitute 16 for n
and simplify.
Step 2 Find the measure of one interior angle.
The int. Ðs are @, so divide by 16.

27. Example 3C: Finding Interior Angle Measures and
Sums in Polygons
Find the measure of each
interior angle of pentagon
ABCDE.
(5 – 2)180° = 540° Polygon Ð Sum Thm.
mÐA + mÐB + mÐC + mÐD + mÐE = 540°
Polygon Ð
Sum Thm.
35c + 18c + 32c + 32c + 18c = 540 Substitute.
135c = 540 Combine like terms.
c = 4 Divide both sides by 135.

28. Example 3C Continued
mÐA = 35(4°) = 140°
mÐB = mÐE = 18(4°) = 72°
mÐC = mÐD = 32(4°) = 128°

29. Check It Out! Example 3a
Find the sum of the interior angle measures of
a convex 15-gon.
(n – 2)180°
(15 – 2)180°
2340°
Polygon Ð Sum Thm.
A 15-gon has 15 sides, so
substitute 15 for n.
Simplify.

30. Check It Out! Example 3b
Find the measure of each interior angle of a
regular decagon.
Step 1 Find the sum of the interior angle measures.
Polygon Ð Sum Thm.
(n – 2)180°
(10 – 2)180° = 1440°
Substitute 10 for n
and simplify.
Step 2 Find the measure of one interior angle.
The int. Ðs are @, so divide by 10.

31. In the polygons below, an exterior angle has been
measured at each vertex. Notice that in each case,
the sum of the exterior angle measures is 360°.

32. Remember!
An exterior angle is formed by one side of a
polygon and the extension of a consecutive side.

34. Example 4A: Finding Interior Angle Measures and
Sums in Polygons
Find the measure of each exterior angle of a
regular 20-gon.
A 20-gon has 20 sides and 20 vertices.
sum of ext. Ðs = 360°.
Polygon Ð Sum Thm.
A regular 20-gon has
20 @ ext. Ðs, so
divide the sum by
20.
measure of one ext. Ð =
The measure of each exterior angle of a regular
20-gon is 18°.

35. Example 4B: Finding Interior Angle Measures and
Sums in Polygons
Find the value of b in polygon
FGHJKL.
Polygon Ext. Ð Sum Thm.
15b° + 18b° + 33b° + 16b° + 10b° + 28b° = 360°
120b = 360 Combine like terms.
b = 3 Divide both sides by 120.

36. Check It Out! Example 4a
Find the measure of each exterior angle of a
regular dodecagon.
A dodecagon has 12 sides and 12 vertices.
sum of ext. Ðs = 360°.
Polygon Ð Sum Thm.
A regular dodecagon
has 12 @ ext. Ðs, so
divide the sum by
12.
measure of one ext.
The measure of each exterior angle of a regular
dodecagon is 30°.

37. Check It Out! Example 4b
Find the value of r in polygon JKLM.
4r° + 7r° + 5r° + 8r° = 360° Polygon Ext. Ð Sum Thm.
24r = 360 Combine like terms.
r = 15 Divide both sides by 24.

38. Example 5: Art Application
Ann is making paper stars for
party decorations. What is the
measure of Ð1?
Ð1 is an exterior angle of a regular
pentagon. By the Polygon Exterior
Angle Sum Theorem, the sum of the
exterior angles measures is 360°.
A regular pentagon has 5 @
ext. Ð, so divide the sum by 5.

39. Check It Out! Example 5
What if…? Suppose the
shutter were formed by 8
blades instead of 10
blades. What would the
measure of each exterior
angle be?
ÐCBD is an exterior angle of a regular octagon. By
the Polygon Exterior Angle Sum Theorem, the sum
of the exterior angles measures is 360°.
A regular octagon has 8 @ ext.
Ð, so divide the sum by 8.

40. Lesson Quiz
1. Name the polygon by the number
of its sides. Then tell whether the
polygon is regular or irregular,
concave or convex.
nonagon; irregular; concave
2. Find the sum of the interior angle
measures of a convex 11-gon.
1620°
3. Find the measure of each interior angle of a
regular 18-gon.
4. Find the measure of each exterior angle of a
regular 15-gon.
160°
24°

41. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.