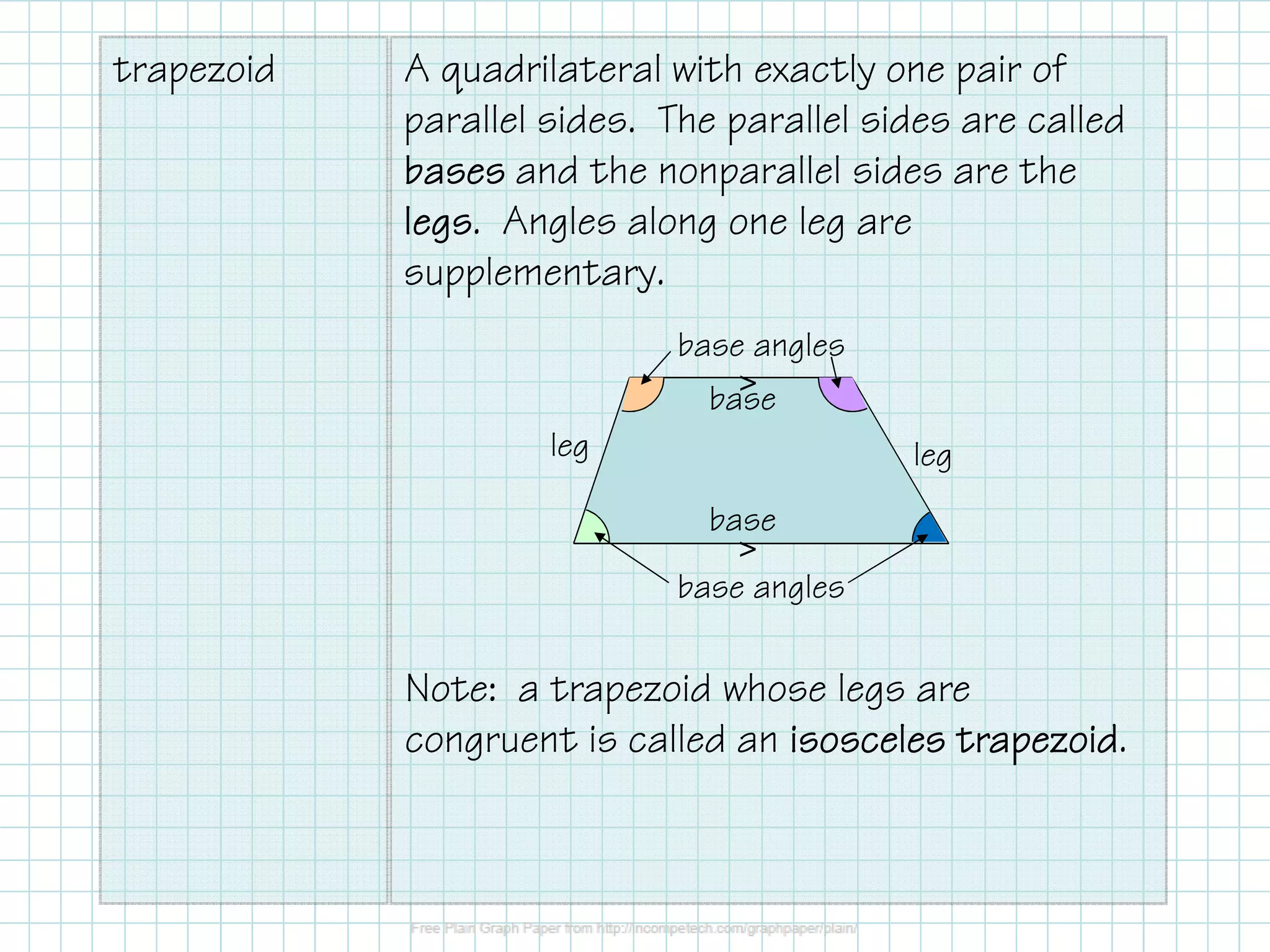
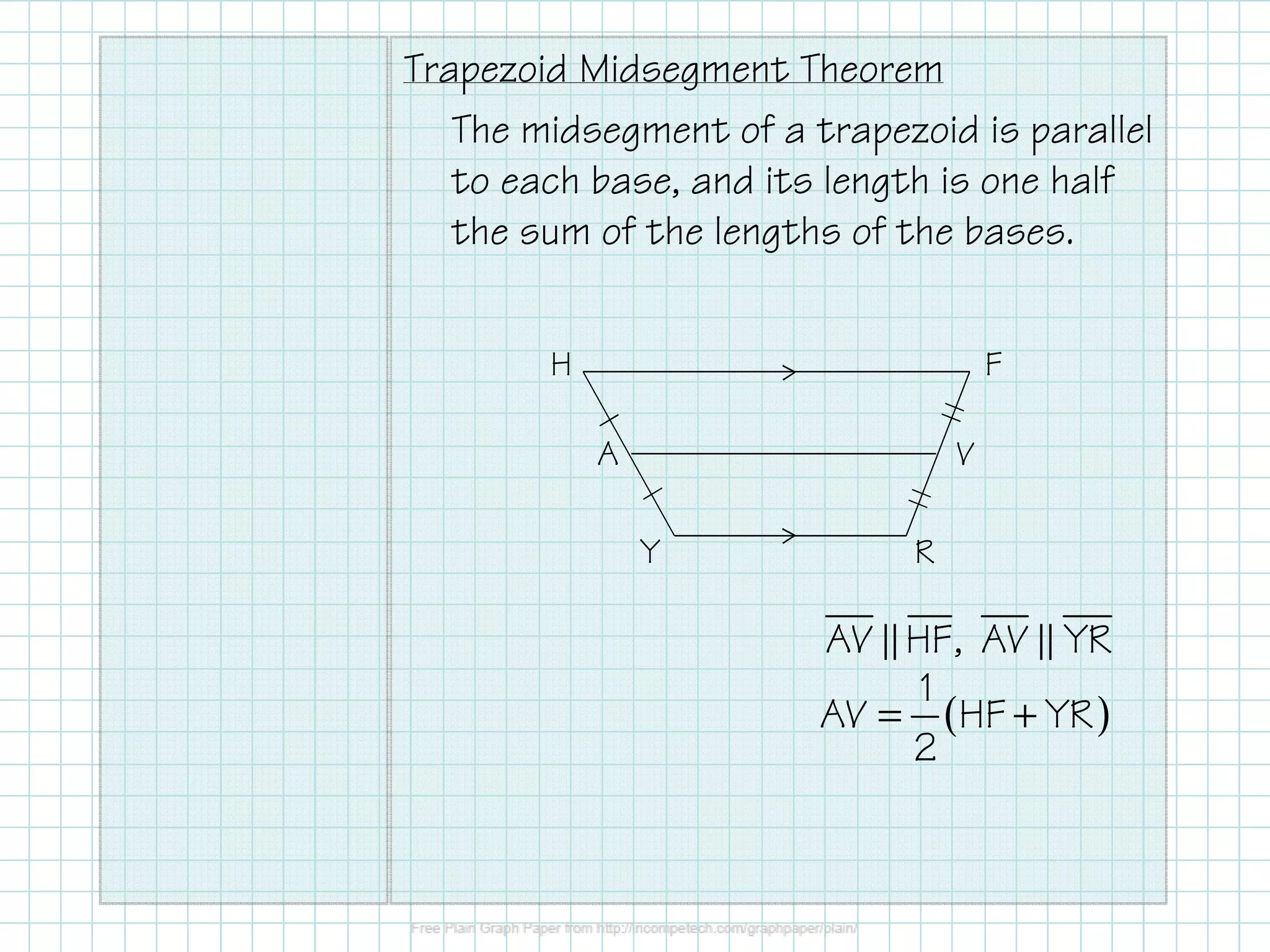
This document defines and provides properties of kites and trapezoids. It states that a kite is a quadrilateral with two pairs of congruent consecutive sides, and its diagonals are perpendicular. A trapezoid has one pair of parallel sides called bases, and the nonparallel sides are legs. An isosceles trapezoid has two congruent base angles. The midsegment of a trapezoid is parallel to the bases and is half the sum of the base lengths. Examples are provided to demonstrate solving problems using properties of kites and trapezoids.

1. 2.7.5 Kites & Trapezoids
The student is able to (I can):
• Use properties of kites and trapezoids to solve problems

2. kite A quadrilateral with exactly two pairs of
congruent consecutive nonparallel sides.
Note: In order for a quadrilateral to be a
kite, nononono sides can be parallel and opposite
sides cannot be congruent.

3. If a quadrilateral is a kite, then its
diagonals are perpendicular.
If a quadrilateral is a kite, then exactly one
pair of opposite angles is congruent.

4. Example In kite NAVY, m∠YNA=54º and
m∠VYX=52º. Find each measure.
1. m∠NVY
90 — 52 = 38º
2. m∠XYN
3. m∠NAV
63 + 52 = 115º
N
A
V
Y
X
−
= = °
180 54 126
63
2 2

5. trapezoid A quadrilateral with exactly one pair of
parallel sides. The parallel sides are called
basesbasesbasesbases and the nonparallel sides are the
legslegslegslegs. Angles along one leg are
supplementary.
Note: a trapezoid whose legs are
congruent is called an isosceles trapezoidisosceles trapezoidisosceles trapezoidisosceles trapezoid.
>
>
base
base
leg leg
base angles
base angles

6. Isosceles Trapezoid Theorems
If a quadrilateral is an isosceles trapezoid,
then each pair of base angles is congruent.
If a trapezoid has one pair of congruent
base angles, then the trapezoid is
isosceles.
A trapezoid is isosceles if and only if its
diagonals are congruent.
>
>
T
R A
P
∠R ≅ ∠A, ∠T ≅ ∠P
TR AP≅
TA RP≅

7. Examples 1. Find the value of x.
5x = 40
x = 8
2. If NS=14 and BA=25, find SE.
SE = 25 — 14 = 11
140º
5xº
B E
AN
SSSS
40º

8. Trapezoid Midsegment Theorem
The midsegment of a trapezoid is parallel
to each base, and its length is one half
the sum of the lengths of the bases.
>
>
H
A
Y
F
V
R
AV HF, AV YR
( )
1
AV HF YR
2
= +

9. Examples is the midsegment of trapezoid OFIG.
1. If OF=22 and GI=30, find MY.
2. If OF=16 and MY=18, find GI.
>
>
O
M
G
F
Y
I
MY
( )
1
MY 22 30 26
2
= + =
( )
1
18 16 GI
2
= +
36 16 GI= +
GI 20=