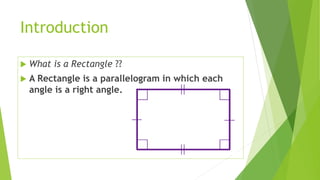
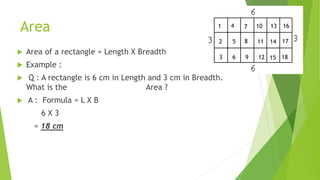
A rectangle is defined as a parallelogram with four right angles, with properties including equal opposite sides and bisecting diagonals. The area is calculated as length times breadth, while the perimeter is twice the sum of length and breadth. The sum of all angles in a rectangle is 360 degrees.

1. Rectangles

2. Introduction
 What is a Rectangle ??
 A Rectangle is a parallelogram in which each
angle is a right angle.

3. Properties
 Opposite sides are parallel and equal
 Each angle is a right angle
 Diagonals are equal
 Diagonals bisect each other

4. Sum of the angles of the
Rectangle
 ABCD is a rectangle. Hence,
 AB II CD , AD II BC , A = C , B = D
 If A is 90◦, then C is also the same.
 B = D ( 90◦)
 A + C = 180◦ ; 90◦ + 90◦ = 180◦
 Sum of all angles is :
 90◦ + 90◦ + 90◦ + 90◦ = 360◦ ; A + B + C + D = 360◦

5. Diagonals of a Rectangle
 A rectangle has two diagonals, they are equal in length
and intersect in the middle.
 The Diagonal is the square root of (width squared +
height squared):
 Diagonal "d" = √(w2 + h2)
 Example:
 Q: A rectangle has a width of 12 cm, and a height of 5
cm, what is the length of a diagonal?
 A: Diagonal Length = √(52 + 122) = √(25 + 144) = √169 = 13
cm

6. Area
 Area of a rectangle = Length X Breadth
 Example :
 Q : A rectangle is 6 cm in Length and 3 cm in Breadth.
What is the n Area ?
 A : Formula = L X B
6 X 3
= 18 cm
1
2
74
5 8
63 9 12 15 18
10 13
1411 17
16

7. Perimeter
 Perimeter of a rectangle = 2 X ( Length + Breadth )
 Example :
 Q : A rectangle has a Length of 6 cm and Breadth of 2 cm.
Find the sdf Perimeter
 A : Formula = 2 X ( L + B )
2 X ( 6 + 2 )
2 X 8
= 16 cm

8. Conclusion
 Diagonal "d" = √(w2 + h2)
 Area of a rectangle = Length X Breadth
 Perimeter of a rectangle = 2 X ( Length + Breadth )
 Sum of all angles in a rectangle = 360
◦

9. n

10. THANK YOU
 Done By :
 Imran (Leader)
 Luqman (PPT)
 Lenoah
 Mobi
 Kabeer
 Hasnain
 Asad