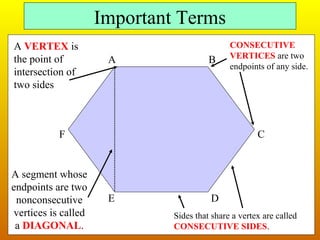
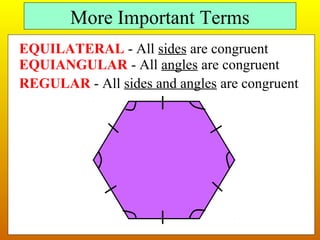
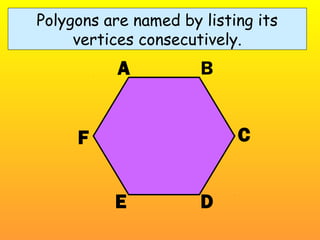
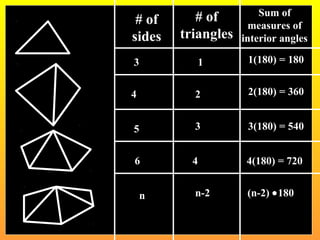
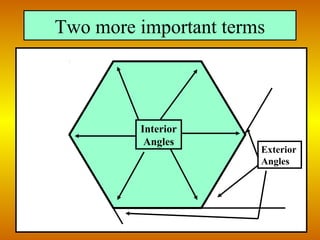
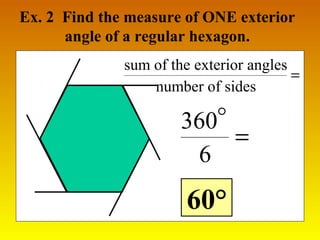
This document provides information about polygons, including definitions of key terms like vertex, diagonal, and consecutive sides and vertices. It explains that polygons are named based on the number of sides, with examples given for triangles, quadrilaterals, pentagons, etc. up to dodecagons. Formulas are provided relating the number of sides of a polygon to the sum of its interior angles and the measure of one interior angle. The terms exterior and interior angles are defined, and an example shows how to use the formula that the sum of exterior angles is 360 degrees to find the measure of one exterior angle of a regular hexagon.

1. INNOVATIVE LESSON
TEMPLATE

3. What ddooeess tthhee wwoorrdd ““ppoollyyggoonn”” mmeeaann??
WWhhaatt iiss tthhee ssmmaalllleesstt nnuummbbeerr ooff
ssiiddeess aa ppoollyyggoonn ccaann hhaavvee??
WWhhaatt iiss tthhee llaarrggeesstt nnuummbbeerr ooff
ssiiddeess aa ppoollyyggoonn ccaann hhaavvee??

4. Triangle
Quadrilateral
Pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Dodecagon
n-gon

5. Hip Bone’s connected to the…
Classifying Polygons
Polygons with 3 sides… Triangles
Polygons with 4 sides… Quadrilaterals
Polygons with 5 sides.. Pentagons
But wait we have more polygons
Polygons with 6 sides… Hexagons
Polygons with 7 sides… Heptagons
Polygons with 8 sides… Octagons
But still we have more polygons
Polygons with 9 sides… Nonagons
Polygons with 10 sides… Decagons
Polygons with 12 sides… Dodecagons
And now we have our polygons

6. F
Important Terms
A B
C
E D
A VERTEX is
the point of
intersection of
two sides
A segment whose
endpoints are two
nonconsecutive
vertices is called
a DIAGONAL.
CONSECUTIVE
VERTICES are two
endpoints of any side.
Sides that share a vertex are called
CONSECUTIVE SIDES.

7. More Important Terms
EQUILATERAL - All sides are congruent
EQUIANGULAR - All angles are congruent
REGULAR - All sides and angles are congruent

8. Polygons are named by listing its
vertices consecutively.
A B
F C
E D

9. # of
sides
# of
triangles
Sum of
measures of
interior angles
3 1 1(180) = 180
4 2 2(180) = 360
5 3 3(180) = 540
6 4 4(180) = 720
n n-2 (n-2) ·180

10. If a convex polygon has n sides,
then the sum of the measure of the
interior angles is
(n – 2)(180°)

11. Ex. 1 Use the regular pentagon to
answer the questions.
A)Find the sum of the
measures of the interior
angles.
540°
B)Find the measure of
ONE interior angle
108°

12. Two more important terms
Exterior
Angles
Interior
Angles

13. If any convex
polygon, the sum of
the measures of the
exterior angles, one at
each vertex, is 360°.
1
2
3
4
5
mÐ1+mÐ2 +mÐ3+mÐ4 +mÐ5 = 360

14. If any convex
polygon, the sum of
the measures of the
exterior angles, one at
each vertex, is 360°.
1
3
2
mÐ1+mÐ2 +mÐ3 = 360

15. If any convex
polygon, the sum of
the measures of the
exterior angles, one at
each vertex, is 360°.
1
3
2
4
mÐ1+mÐ2 +mÐ3+mÐ4 = 360

16. Ex. 2 Find the measure of ONE exterior
angle of a regular hexagon.
sum of the exterior angles
number of sides

=
60°
=
360
6

17. Ex. 4 Each exterior angle of a polygon
is 18°. How many sides does it have?
exterior angle
sum of the exterior angles =
n = 20
number of sides
360 
=18
n