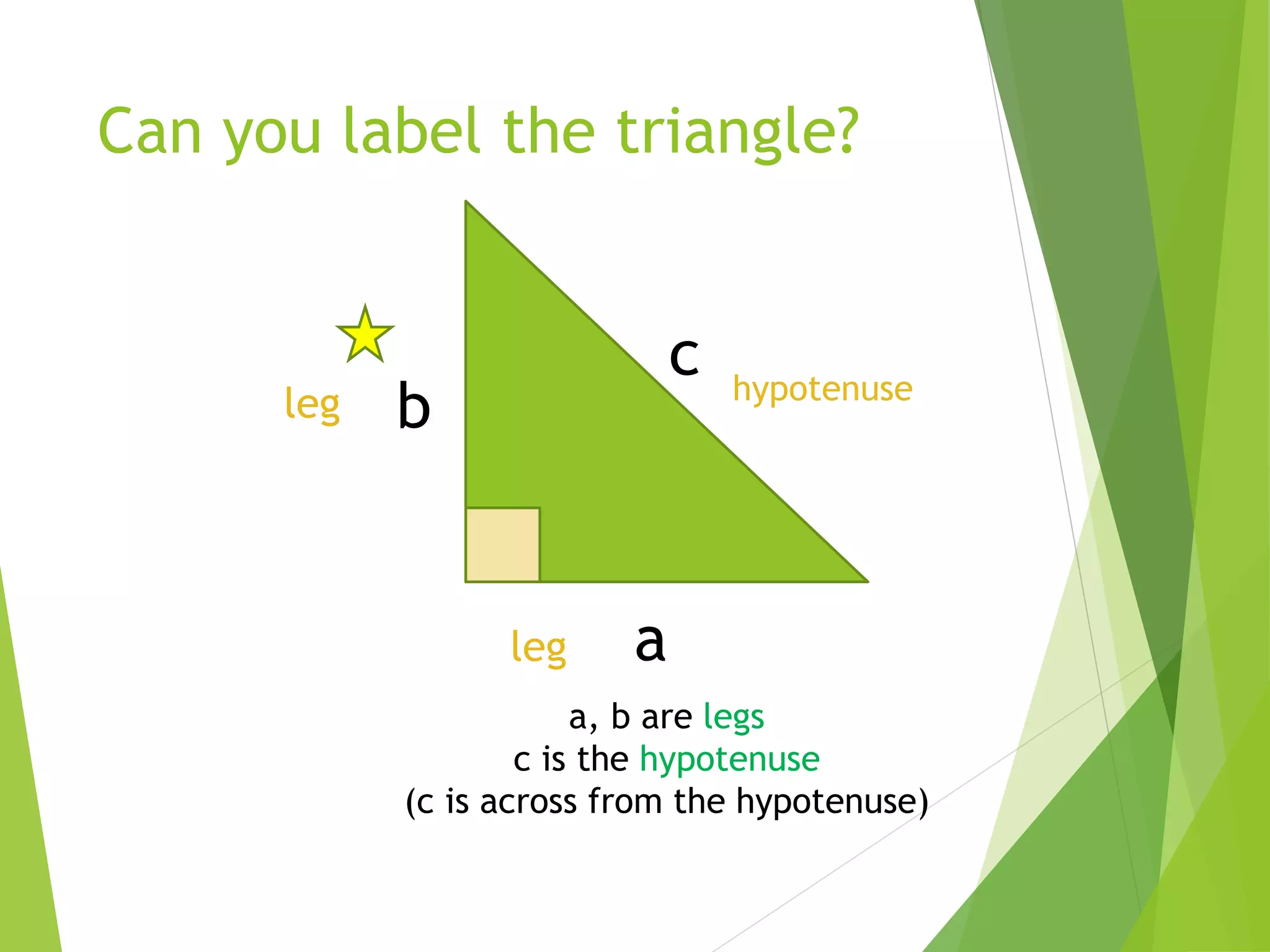
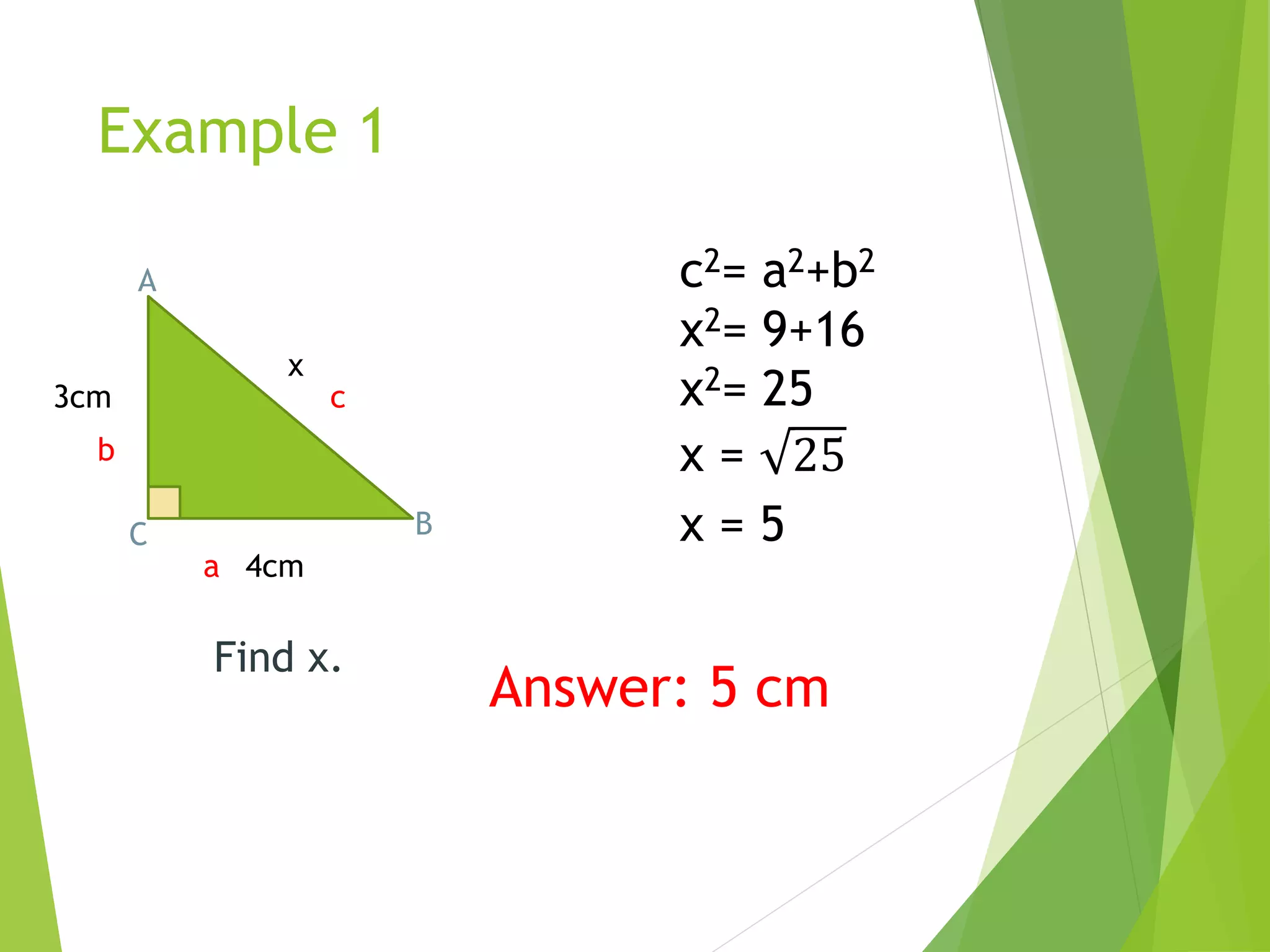
This document discusses the Pythagorean theorem. It begins with an introduction of the theorem, followed by examples of using it to solve for the length of a triangle's hypotenuse given the lengths of the other two sides. The document then provides task cards with real world problems for students to solve using the Pythagorean theorem. It concludes with a post-test asking students to use the theorem to find hypotenuse lengths.

1. Pythagorean Theorem
𝑎2
+ 𝑏2
= 𝑐2

2. Pre-Test
Directions: Determine, to 2 decimal
places, the length of the hypotenuse of
the right-angled triangles whose two
shorter sides have the lengths given
below.
1.) 2 cm and 5 cm
2.) 1 cm and 2 cm
3.) 8 cm and 9 cm
4.) 1 cm and 1 cm
5.) 1.73 cm and 1 cm

3. What is a
hypotenuse?

4. http://m.youtube.com/watch?v=AhFjfCdG61Y

5. Where did this come
from???
Over 2,500 years ago, a Greek
mathematician named Pythagoras
popularized the concept that a
relationship exists between the
and the of
and that this relationship is
true for right triangles.

6. Pythagoras
 The Egyptians knew of this concept, as it
related to 3, 4, 5 right triangles, long
before the time of Pythagoras. It was
Pythagoras, however, who generalized the
concept and who is attributed with its
first geometrical demonstration. Thus, it
has become known as the Pythagorean
Theorem.

7. = the Pythagorean Theorem
"In any right triangle, the square of the length of the
hypotenuse is equal to the sum of the squares of the
lengths of the legs.“
This relationship can be stated as:
For any RIGHT TRIANGLE
𝑎2
+ 𝑏2
= 𝑐2
𝑎2
+ 𝑏2
= 𝑐2

8. Can you label the triangle?
b
c
a
a, b are legs
c is the hypotenuse
(c is across from the hypotenuse)
leg hypotenuse
leg

9. Example 1
A
BC
3cm
4cm
x
a
b
c
c2= a2+b2
x2= 9+16
x2= 25
x = 25
x = 5
Answer: 5 cm
Find x.

10. Example 2
A
BC
5cm
12cm
x
a
b
c
c2= a2+b2
x2= 25+144
x2= 169
x = 169
x = 13
Answer: 13 cm
Find x.

11. Example 3
A
BC
7cm
24cm
x
a
b
c
c2= a2+b2
x2= 49+576
x2= 625
x = 625
x = 25
Answer: 25 cm
Find x.

12. Task Card
Group 1
1. Road Trip: Let’s say two friends are
meeting at a playground. Mary is already at
the park but their friend Bob needs to get
there taking the shortest path possible. Bob
has two ways he can go – he can follow the
roads getting to the park – first heading
south 3 miles, then heading west four miles.
The total distance covered following the
roads will be 7 miles. The other way he can
get there is by cutting through some open
fields and walk directly to the park.

13. Task Card
Group 2
2. Painting on a Wall: Painters use ladders to
paint on high buildings and often use the help
of Pythagorean Theorem to complete their
work. The painter needs to determine how tall
a ladder needs to be in order to safely place
the base away from the wall so it won’t tip
over. In this case the ladder itself will be the
hypotenuse. Take for example a painter who
has to paint a wall which is about 3m high. The
painter has to put the base of the ladder 2m
away from the wall to ensure it won’t tip. What
will be the length of the ladder required by the
painter to complete his work?

14. Task Card
Group 3
3. What T.V. Size Should You Buy?:
Mr. James saw an advertisement of a
T.V. in the newspaper where it is
mentioned that the T.V. is 16 inches
high and 14 inches wide. Calculate
the diagonal length of its screen for
Mr. James by using Pythagorean
Theorem.

15. Task Card
Group 4
4. Finding the Right Sized Computer:
Mary wants to get a computer monitor
for her desk which can hold a 22-inch
monitor. She has found a monitor 16
inches wide and 10 inches high. Will
the computer fit into Mary’s cabin?

16. Post-Test
 Directions: Determine, to 2 decimal places, the length
of the hypotenuse of the right-angled triangles whose
two shorter sides have the lengths given below.
 1.) 2 cm and 5 cm
 2.) 1 cm and 2 cm
 3.) 8 cm and 9 cm
 4.) 1 cm and 1 cm
 5.) 1.73 cm and 1 cm

17. Post-Test
Directions: Determine, to 2 decimal
places, the length of the hypotenuse of
the right-angled triangles whose two
shorter sides have the lengths given
below.
1.) 2 cm and 5 cm
2.) 1 cm and 2 cm
3.) 8 cm and 9 cm
4.) 1 cm and 1 cm
5.) 1.73 cm and 1 cm