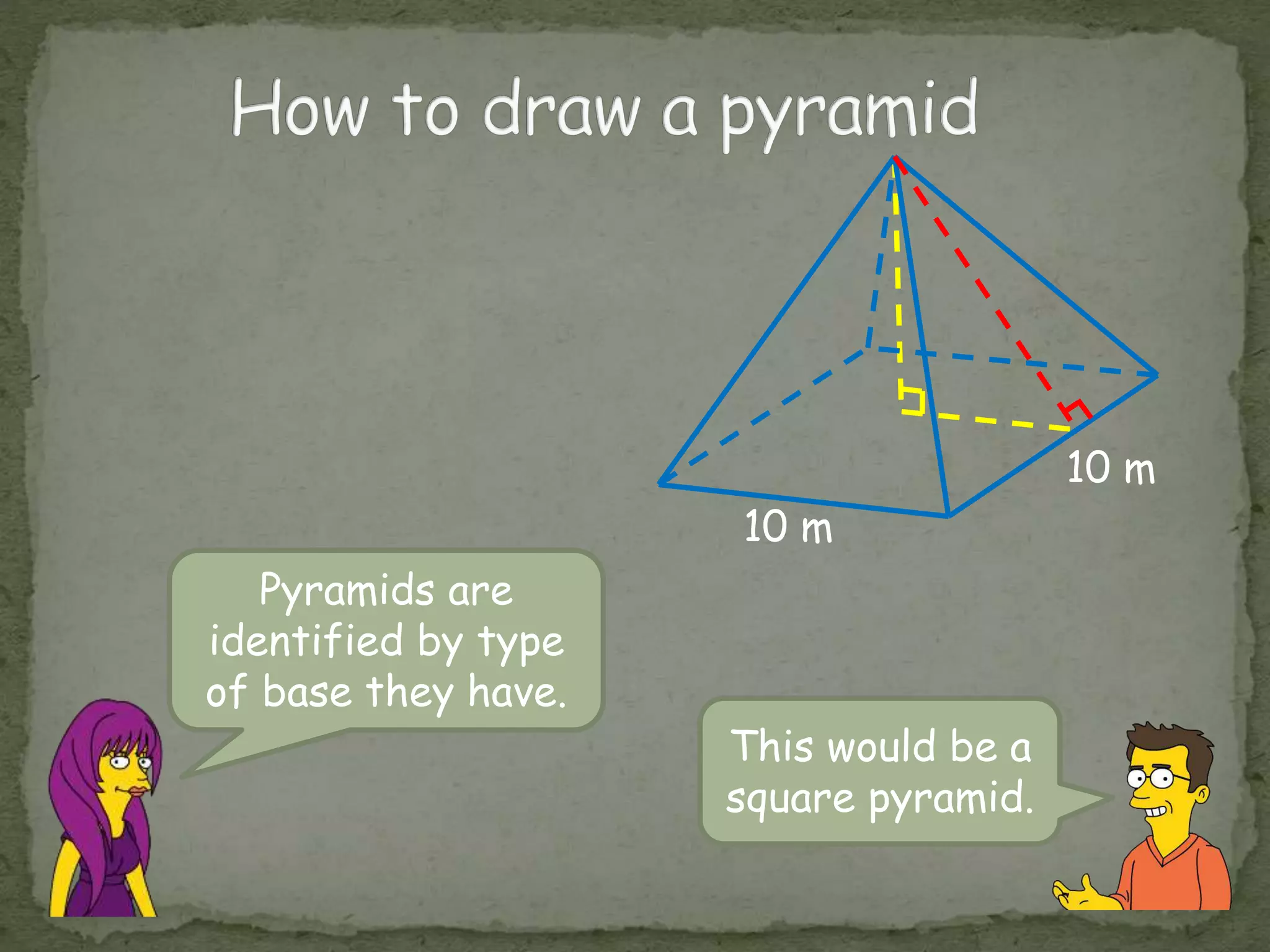
This document discusses the volume formula for pyramids and provides examples of calculating the volume of different square pyramids using the formula V = 1/3 * B * h, where B is the area of the base and h is the height. It defines key pyramid terms like apex, base, and identifies pyramids by their base type. Sample problems provide the side length of a square base and height to calculate the volume. Review questions test the reader's understanding of pyramid features and volume calculation.

1. Math Rocks!
푉 =
1
3
퐵ℎ

2. Pyramid – A solid object where the base
is a polygon and the sides are triangles
which meet at the top
All polygons have
straight sides.
Apex
10 m
10 m
The apex is
highest point.
Base

3. Pyramids are
identified by type
of base they have.
This would be a
square pyramid.
10 m
10 m

4. The dashed lines will
indicate lines hidden
by a solid polygon.
Draw lines from the
four vertices to an
apex above the
rhombus.

5. 10 m
Solve for volume
10 m
퐵 = 퐴푟푒푎 표푓 퐵푎푠푒
Why must you use the
Pythagorean theorem?
To find the height
of the pyramid.
푉 =
1
3
퐵ℎ
푎2 + 52 = 132
푎2 + 25 = 169
푎2 = 144
푎 = 12
ℎ = ℎ푒푖푔ℎ푡 표푓 푝푦푟푎푚푖푑
ℎ = 12 푚
13 m
퐵 = 10 푚 ∙ 10 푚 = 100 푚2

6. 10 m
10 m
퐵 100 푚2
How do we
proceed?
Just substitute
and solve.
13 m
12 m
푉 =
1
3
100 푚2 12 푚
푉 =
1
3
1200 푚3
푉 = 400 푚3
푉 =
1
3
퐵ℎ
ℎ = 12 푚

8. h=481 ft.
s=756 ft.
h=height
s=side of base
B= side squared
What must you do
after substituting
the values? Follow the order
of operations.
푉 =
1
3
571,536 푓푡2 481 푓푡
푉 =
1
3
756 푓푡 2 ∙ 481 푓푡
푉 =
1
3
274,908,816 푓푡3
푉 = 91,636,272 푓푡3

10. h=24 m
s=55 m
h=height
s=side of base
B= side squared
1
3
1
3
55 푚 2 ∙ 24 푚
3,025 푚2 24 푚
1
3
Why do
푉 =
푉 =
푉 =
72,600 푚3
mummies tell
no secrets?
Because they
keep things
under wraps.
푉 = 24,200 푚3

12. h=72 ft.
s=112 ft.
h=height
s=side of base
B= side squared
Why might you want
to know the volume
of the Louvre.
푉 =
1
3
12,544 푓푡.2 72 푓푡.
푉 =
1
3
112 푓푡. 2 ∙ 72 푓푡.
푉 =
1
3
903,168 푓푡.3
For heating and
cooling purposes.
푉 = 301, 056 푓푡.3

14. h=65 m
s=225 m
h=height
s=side of base
B= side squared
Who belongs to
the Pyramid
PTA?
푉 =
1
3
50,625 푚2 65 푚
푉 =
1
3
225 푚 2 ∙ 65 푚
푉 =
1
3
3,290,625 푚3
Mummies and
Deadies!
푉 = 1,096,875 푚3

16. For this problem you
are not give the side of
the square base, but
the perimeter.
푃 =
2,600 푓푡
4
푃 = 650 푓푡.
Divide the
perimeter by four.

17. h=350 ft.
s=650 ft.
h=height
s=side of base
B= side squared
Why couldn’t the
mummy answer the
phone?
푉 =
1
3
422,500 푓푡.2 350 푓푡.
푉 =
1
3
650 푓푡. 2 ∙ 350 푓푡.
푉 =
1
3
147,875,000 푓푡.3
She was
tied up!
푉 = 49,291,667푓푡.3

18. Review Questions
What information is not needed to find the volume?
The height of the triangle face.
What do you call the top of a pyramid?
Apex
When give the perimeter of the base, how do you find the
side of the base?
Divide the perimeter by four.
Do mummies enjoy Of corpse!
being mummies.

19. Review Questions
How do you identify a pyramid?
By the type of base.
What would you call a pyramid in which all the sides of the
base are congruent with right angles?
A square pyramid
If you did not want
multiply by one-third
what else could you do?
Divide by 3
1
퐵ℎ
퐵ℎ =
3
3

20. If you are not a Math Monkey
then you are a chimp.
Copyright © 2013 Daryle Fleming
All rights reserved by author.
Permission to copy for single classroom use only.
Electronic distribution limited to single classroom use only.
Not for public display.