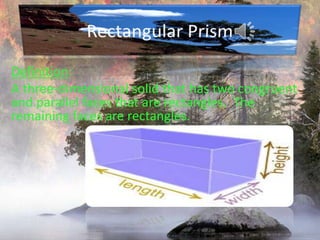
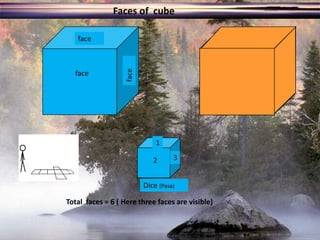
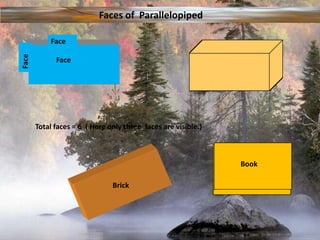
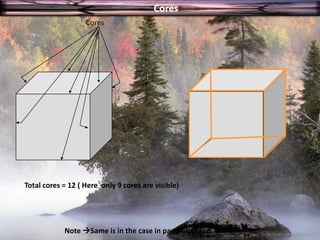
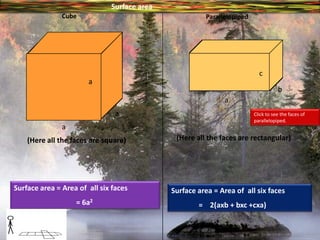
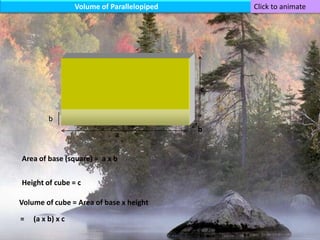
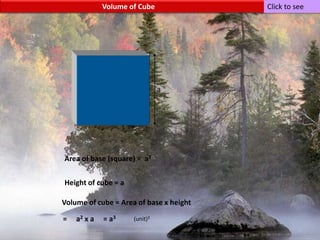
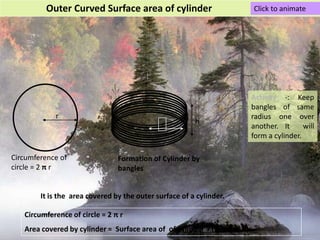
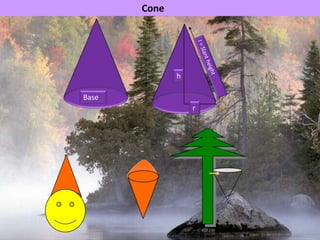
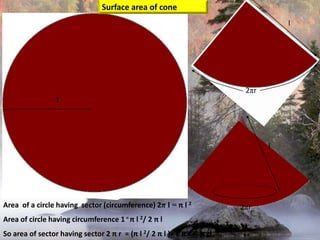
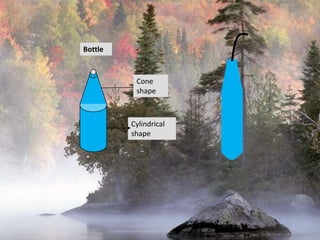
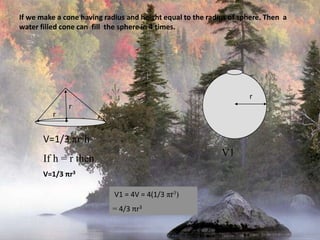
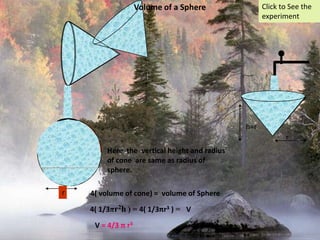
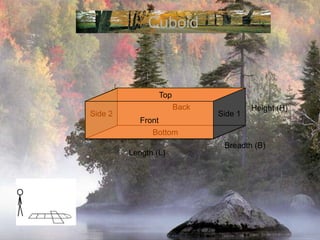
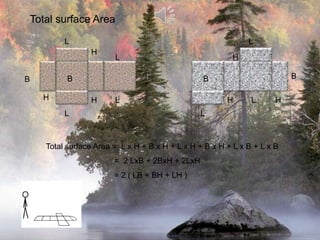
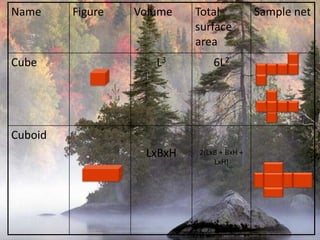
The document provides information on surface area and volume formulas and calculations for basic 3D shapes including prisms, cubes, cylinders, cones, and spheres. It defines key terms like surface area and volume and provides example calculations and formulas for finding the surface area and volume of cubes, rectangular prisms, cylinders, cones, and spheres. Diagrams and examples are included to illustrate the different shapes and how to set up the surface area and volume calculations.

1. Slide showOn Mathematics Exercise 13Topic on Surface Area and Volume

2. Surface Area and VolumeVocabulary & Formulas

3. PrismDefinition:A three-dimensional solid that has two congruent and parallel faces that are polygons. The remaining faces are rectangles. Prisms are named by their faces.

4. Rectangular PrismDefinition:A three-dimensional solid that has two congruent and parallel faces that are rectangles. The remaining faces are rectangles.

5. CubeDefinition:A rectangular prism in which all faces are congruent squares.

6. Surface AreaDefinition:The sum of the areas of all of the faces of a three-dimensional figure.Ex. How much construction paper will I need to fit on the outside of the shape?

7. VolumeDefinition:The measure in cubic units of the interior of a solid figure; or the space enclosed by a solid figure.Ex. How much sand will it hold?

8. Surface Area of a Rectangular PrismEx:How much construction paper would I need to fit on the outside of a particular rectangular prism?Formula:S.A. = 2LW + 2Lh + 2Wh

9. Surface Area of a CubeEx:How much construction paper would I need to fit on the outside of a particular cube?Formula:S.A. = 6s2

10. Volume of a Rectangular PrismEx:How much sand would I need to fill the inside of a particular rectangular prism?Formula:V = L*W*h

11. Volume of a CubeEx:How much sand would I need to fill the inside of a particular cube?Formula:V = s3

12. Surface area and volume of different Geometrical FiguresCubeCylinderParallelopipedCone

13. facefaceface1Dice (Pasa)32 Faces of cubeTotal faces = 6 ( Here three faces are visible)

14. FaceFaceFaceBookBrickFaces of ParallelopipedTotal faces = 6 ( Here only three faces are visible.)

15. CoresCoresTotal cores = 12 ( Here only 9 cores are visible)Note Same is in the case in parallelopiped.

16. Surface areaCube Parallelopiped cabaaClick to see the faces of parallelopiped.a(Here all the faces are rectangular)(Here all the faces are square)Surface area = Area of all six faces = 6a2Surface area = Area of all six faces = 2(axb + bxc +cxa)

17. Volume of ParallelopipedClick to animate cbbaArea of base (square) = a x bHeight of cube = cVolume of cube = Area of base x height = (a x b) x c

18. Volume of CubeClick to seeaaaArea of base (square) = a2Height of cube = aVolume of cube = Area of base x height = a2 x a = a3(unit)3

19. Outer Curved Surface area of cylinderrrhClick to animate Activity -: Keep bangles of same radius one over another. It will form a cylinder.Circumference of circle = 2 π rFormation of Cylinder by banglesIt is the area covered by the outer surface of a cylinder.Circumference of circle = 2 π rArea covered by cylinder = Surface area of of cylinder = (2 π r) x( h)

20. Total Surface area of a solid cylinderCurved surfacecircular surfacesArea of curved surface +area of two circular surfaces==(2 π r) x( h) + 2 π r2= 2 π r( h+ r)

21. r Other method of Finding Surface area of cylinder with the help of paperhh2πrSurface area of cylinder = Area of rectangle= 2 πrh

22. rhVolume of cylinderVolume of cylinder = Area of base x vertical height= π r2xh

23. Conel = Slant heighthBaser

24. Volume of a ConeClick to See the experimenthhHere the vertical height and radius of cylinder & cone are same.rr3( volume of cone) = volume of cylinder3( V) = π r2hV = 1/3 π r2h

25. if both cylinder and cone have same height and radius then volume of a cylinder is three times the volume of a cone ,Volume = 3V Volume =V

26. Mr. Mohan has only a little jar of juice he wants to distribute it to his three friends. This time he choose the cone shaped glass so that quantity of juice seem to appreciable.

27. Surface area of conel2πrll2πrArea of a circle having sector (circumference) 2π l = π l 2Area of circle having circumference 1 = π l 2/ 2 π l So area of sector having sector 2 π r = (π l 2/ 2 π l )x 2 π r = π rl

28. Comparison of Area and volume of different geometrical figures

29. Area and volume of different geometrical figuresrrrr/√2l=2rr

30. Total surface Area and volume of different geometrical figures and naturerrrl=3r r1.44r22rSo for a given total surface area the volume of sphere is maximum. Generally most of the fruits in the nature are spherical in nature because it enables them to occupy less space but contains big amount of eating material.

31. Think :- Which shape (cone or cylindrical) is better for collecting resin from the treeClick the next

32. 3rrrV= 1/3π r2(3r)V= π r3Long but Light in weightSmall niddle will require to stick it in the tree,so little harm in treeV= π r2 (3r) V= 3 π r3Long but Heavy in weightLong niddle will require to stick it in the tree,so much harm in tree

33. BottleCone shapeCylindrical shape

34. r V1If we make a cone having radius and height equal to the radius of sphere. Then a water filled cone can fill the sphere in 4 times.rrV=1/3 πr2hIf h = r thenV=1/3 πr3 V1 = 4V = 4(1/3 πr3) = 4/3 πr3

35. Volume of a SphereClick to See the experimentrrh=rHere the vertical height and radius of cone are same as radius of sphere.4( volume of cone) = volume of Sphere4( 1/3πr2h) = 4( 1/3πr3 ) = VV = 4/3 π r3

36. Volumeis the amount of space occupied by any 3-dimensional object.1cm1cm1cmVolume = base area x height = 1cm2 x 1cm = 1cm2

37. BackTopSide 2Side 1FrontBottomCuboidBackTopSide 2Side 1FrontHeight (H)BottomBreadth (B)Length (L)

38. The netLHHLHBBBBLHHHLBBL

39. Total surface AreaLLHLHBBBBHHLHHLLLTotal surface Area = L x H + B x H + L x H + B x H + L x B + L x B = 2 LxB + 2BxH + 2LxH = 2 ( LB + BH + LH )

41. CubeLLLVolume = Base area x height = L x L x L = L3Total surface area = 2LxL + 2LxL + 2LxL = 6L2

42. Sample netTotal surface areaVolumeFigureName6L2L3Cube2(LxB + BxH + LxH)LxBxHCuboid

43. Show ends