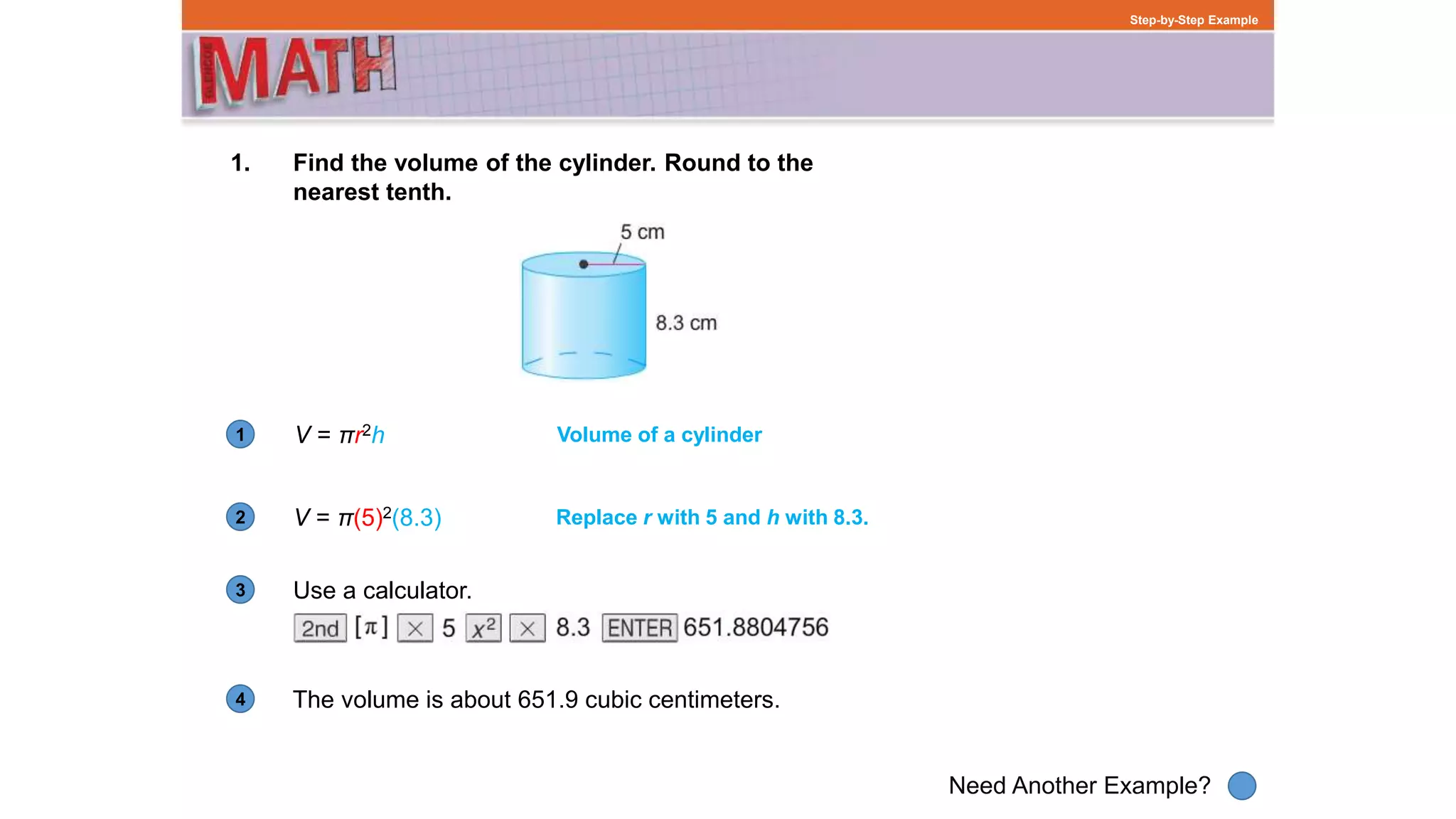
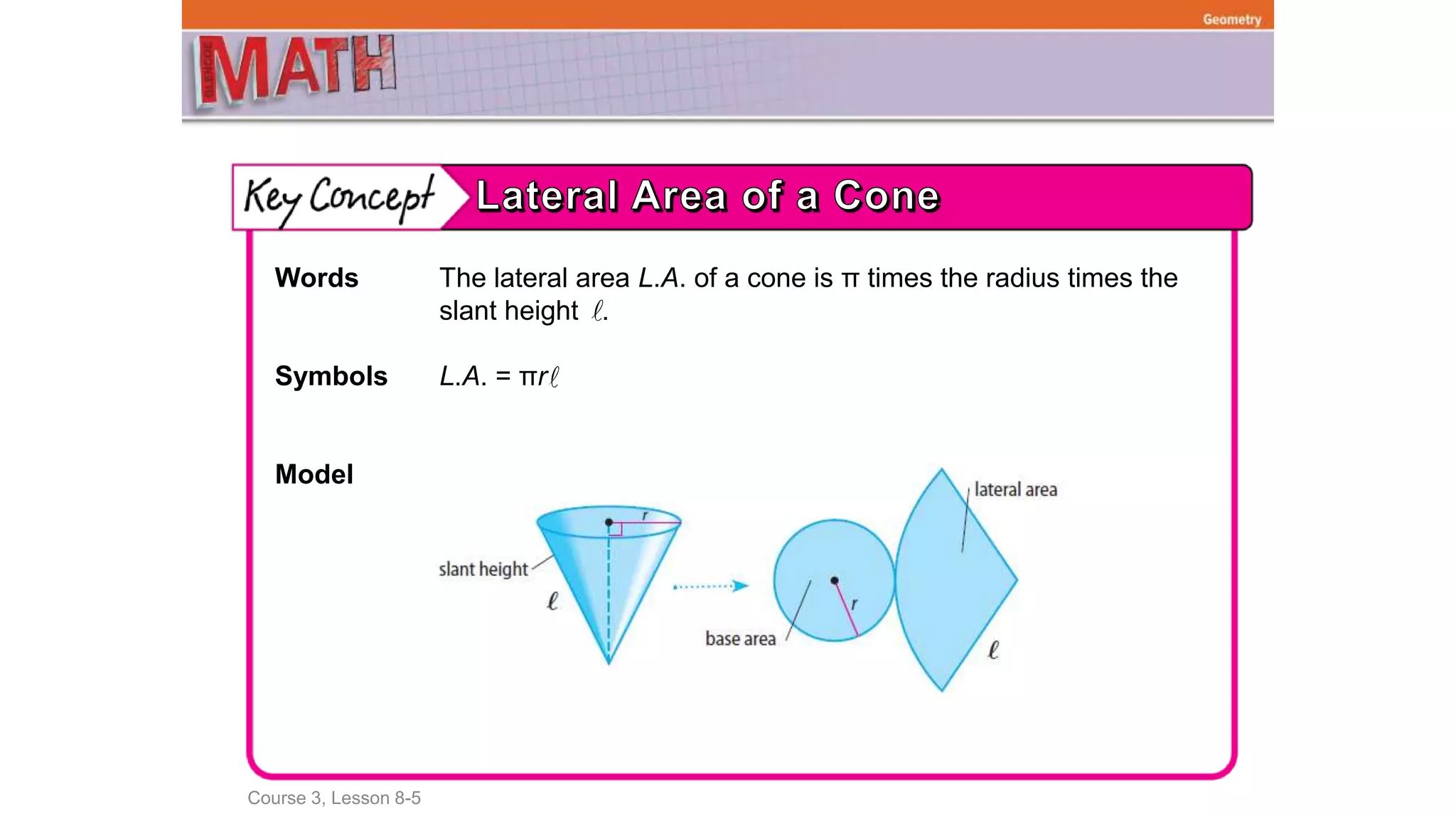
The document provides examples for calculating the volumes and surface areas of various geometric solids like cylinders, cones, spheres, and similar solids. It defines the formulas used to find the volume and surface area of each solid type and provides step-by-step worked examples of applying the formulas. The examples demonstrate how to find the volume or surface area by identifying the relevant measurements in the problem, substituting them into the correct formula, and calculating the result.

1. To
• find the volume of a cylinder,
• find the volume of a composite figure
that includes cylinders
Course 3, Lesson 8-1
Geometry

2. Course 3, Lesson 8-1
Geometry
Words The volume V of a cylinder with radius r is the area of the base
B times the height h.
Model
Symbols V = Bh, where B = πr2 or V = πr2h

3. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Find the volume of the cylinder. Round to the
nearest tenth.
V = πr2h Volume of a cylinder
V = π(5)2(8.3) Replace r with 5 and h with 8.3.
Use a calculator.
The volume is about 651.9 cubic centimeters.

4. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. Find the volume of a cylinder with a diameter of 16 inches
and a height of 20 inches. Round to the nearest tenth.
V = πr2h Volume of a cylinder
V = π(8)2(20) The diameter is 16 so the radius is 8. Replace h with 20.
The volume is about 4,021.2 cubic inches.
Use a calculator.V ≈ 4,021.2

5. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
3. A metal paperweight is in the shape of a cylinder. The paperweight
has a height of 1.5 inches and a diameter of 2 inches. How much
does the paperweight weigh if 1 cubic inch weighs 1.8 ounces?
Round to the nearest tenth.
V = πr2h Volume of a cylinder
V = π(1)21.5 Replace r with 1 and h with 1.5.
First find the volume of the paperweight.
V ≈ 4.7
To find the weight of the paperweight, multiply the volume by 1.8.
4.7(1.8) = 8.46
Simplify
So, the weight of the paperweight is about 8.5 ounces.

6. 1
Need Another Example?
2
3
Step-by-Step Example
4. Tanya uses cube-shaped
beads to make jewelry.
Each bead has a circular
hole through the middle.
Find the volume of each
bead.
Rectangular Prism
The bead is made of one rectangular prism and one cylinder. Find the
volume of each solid. Then subtract to find the volume of the bead.
The volume of the bead is 1,728 – 37.7 or 1,690.3 cubic millimeters.
Cylinder
V = Bh
V = (12 • 12)12 or 1,728
V = Bh
V = (π • 12)12 or 37.7

7. To
• find the volume of a cone
Course 3, Lesson 8-2
Geometry

8. Course 3, Lesson 8-2
Geometry
Words The volume V of a cone with radius r is one third the
area of the base B times the height h.
Model
Symbols V = Bh or V = πr2h
1
3
1
3

9. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Find the volume of the cone. Round to the nearest tenth.
V = πr2h Volume of a cone
V = • π • 32 • 6 r = 3, h = 6
V ≈ 56.5 Simplify
The volume is about 56.5 cubic inches.

10. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. A cone-shaped paper cup is filled with water. The height of the cup
is 10 centimeters and the diameter is 8 centimeters. What is the
volume of the paper cup? Round to the nearest tenth.
V = πr2h Volume of a cone
r = 4, h = 10
V ≈ 167.6 Simplify
The volume of the paper cup is about 167.6 cubic centimeters.
V = • π • 42 • 10

11. 1
Need Another Example?
2
3
Step-by-Step Example
3. Find the volume of the solid.
Round to the nearest tenth.
Find the volume of the cylinder.
Volume of a cylinder
So, the volume of the solid is about 201.1 + 83.8 or
284.9 cubic feet.
Find the volume of the cone.
Volume of a cone
V = π • 42 • 4
V = π • 16 • 4
V ≈ 201.1
V = πr2h
r = 4, h = 4
Simplify
Simplify
V = πr2h
V = π • 42 • 5
V = π • 16 • 5
V ≈ 83.8
r = 4, h = 5
Simplify
Simplify

12. To
• find the volume of a sphere and a
hemisphere
Course 3, Lesson 8-3
Geometry

13. Course 3, Lesson 8-3
Geometry
Words The volume V of a sphere is four thirds the product
of π and the cube of the radius r.
Model
Symbols V = πr3
4
3

14. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Find the volume of the sphere.
Round to the nearest tenth.
V = πr3
The volume of the sphere is about 904.8 cubic millimeters.
Volume of a sphere
V = • • π • 63 Replace r with 6.
V ≈ 904.8 Simplify. Use a calculator.

15. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. A spherical stone in the courtyard of the National Museum of Costa
Rica has a diameter of about 8 feet. Find the volume of the spherical
stone. Round to the nearest tenth.
The volume of the spherical stone is about 268.1 cubic feet.
Volume of a sphere
Replace r with 4.
V ≈ 268.1 Simplify. Use a calculator.
V = • π • 43
V = πr3

16. 1
Need Another Example?
2
3
4
Step-by-Step Example
3. A volleyball has a diameter of 10 inches. A pump can inflate the ball at
a rate of 325 cubic inches per minute. How long will it take to inflate
the ball? Round to the nearest tenth.
Find the volume of the ball. Then use a proportion.
Volume of a sphere
V = π • 53 or 523.6 Replace r with 5.
325x = 523.6 Cross multiply.
x = 1.6 Simplify.
Write the proportion.
So, it will take about 1.6 minutes to inflate the ball.
V = πr3

17. 1
Need Another Example?
2
3
4
Step-by-Step Example
4. Find the volume of the hemisphere. Round to the nearest tenth.
V = πr3 Volume of a hemisphere
V = • π • 53 Replace r with 5.
V ≈ 261.8 Simplify. Use a calculator.
The volume of the hemisphere is about 261.8 cubic centimeters.

18. To
• find the lateral and total surface area of a
cylinder
Course 3, Lesson 8-4
Geometry

19. Course 3, Lesson 8-4
Geometry
Lateral Area
Words The lateral area L.A. of a cylinder with height h and
radius r is the circumference of the base times the height.
Symbols L.A. = 2πrh
Total Surface Area
Words The surface area S.A. of a cylinder with height h and radius r is
the lateral area plus the area of the two circular bases.
Symbols S.A. = L.A. + 2πr2 or S.A. = 2πrh + 2πr2
Model

20. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Find the surface area of the cylinder. Round to the nearest tenth.
S.A. = 2πrh + 2πr 2
The surface area is about 113.1 square meters.
Surface area of a cylinder
S.A. = 2π(2)(7) + 2π(2)2 Replace r with 2 and h with 7.
S.A. ≈ 113.1 Simplify

21. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. A circular fence that is 2 feet high is to be built around the outside of a
carousel. The distance from the center of the carousel to the edge of the
fence will be 35 feet. What is the area of the fencing material that is
needed to make the fence around the carousel?
L.A. = 2πrh
You need to find the lateral area. The radius of the circular fence is 35 feet.
The height is 2 feet.
Lateral area of a cylinder
L.A. = 2π(35)(2) Replace r with 35 and h with 2.
L.A. ≈ 439.8 Simplify
5 So, about 439.8 square feet of material is needed to make the fence.

22. To
• find the lateral and total surface area of a
cone
Course 3, Lesson 8-5
Geometry

23. Course 3, Lesson 8-5
Geometry
Words The lateral area L.A. of a cone is π times the radius times the
slant height .
Symbols L.A. = πr
Model

24. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Find the lateral area of the cone. Round to the nearest tenth.
L.A. = πrℓ
The lateral area of the cone is about 204.2 square millimeters.
Lateral area of a cone
L.A. = π • 5 • 13 Replace r with 5 and ℓ with 13.
L.A. ≈ 204.2 Simplify

25. Course 3, Lesson 8-5
Geometry
Words The surface area S.A. of a cone with slant height ℓ and radius r
is the lateral area plus the area of the base.
Symbols S.A. = L.A. + πr2 or S.A. = πr + πr2

26. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. Find the surface area of the cone. Round to the nearest tenth.
S.A. = πrℓ + πr2
The surface area of the cone is about 230.0 square inches.
Surface area of a cone
S.A. = π • 6 • 6.2 + π • 62 Replace r with 6 and ℓ with 6.2.
S.A. ≈ 230.0 Simplify

27. 1
Need Another Example?
2
3
4
Step-by-Step Example
3. A tepee has a radius of 5 feet and a slant height of 12 feet.
Find the lateral area of the tepee. Round to the nearest tenth.
L.A. = πrℓ
The lateral area of the tepee is about 188.5 square feet.
Lateral area of a cone
L.A. = π • 5 • 12 Replace r with 5 and ℓ with 12.
L.A. ≈ 188.5 Simplify

28. To
• find the surface area and volume of
similar solids
Course 3, Lesson 8-6
Geometry

29. Course 3, Lesson 8-6
Geometry
Words If Solid X is similar to Solid Y by a scale factor, then the
surface area of X is equal to the surface area of Y times the
square of the scale factor.

30. 1
Need Another Example?
2
3
Step-by-Step Example
1. The surface area of a rectangular prism is 78 square centimeters.
What is the surface area of a similar prism that is 3 times as large?
S.A. = 78 × 32 Multiply by the square of the scale factor.
S.A. = 78 × 9 Square 3.
S.A. = 702 cm2 Simplify

31. Course 3, Lesson 8-6
Geometry
Words If Solid X is similar to Solid Y by a scale factor, then the
volume of X is equal to the volume of Y times the cube of the
scale factor.

32. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. A triangular prism has a volume of 432 cubic yards. If
the prism is reduced to one third its original size, what
is the volume of the new prism?
V = 432 × Multiply by the cube of the scale factor.
V = 432 ×
V = 16 yd3 Simplify
The volume of the new prism is 16 cubic yards.
Cube .

33. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
3. The measurements for a standard hockey puck are
shown at the right. A giant hockey puck is 40 times
the size of a standard puck. Find the volume and
surface area of the giant puck. Use 3.14 for π.
Find the volume and surface area of the standard puck first.
V = πr2h
Find the volume and surface area of the giant puck using the computations
for the standard puck and the scale factor.
V = V(40)3
S.A. = S.A.(40)2
The giant hockey puck has a volume of about 452,160 cubic inches
and a surface area of about 37,680 square inches.
= (7.065)(40)3
= 452,160 in3
≈ (3.14)(1.5)2(1)
≈ 7.065 in3
= (23.55)(40)2
= 37,680 in2
S.A. = 2(πr2) + 2πrh
≈ 14.13 + 9.42
≈ 23.55 in2
≈ 2(3.14)(1.5)2 + 2(3.14)(1.5)(1)