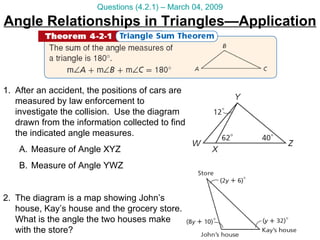
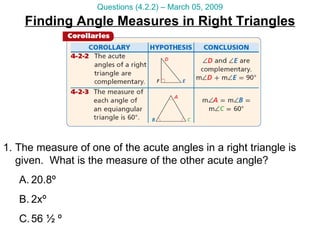
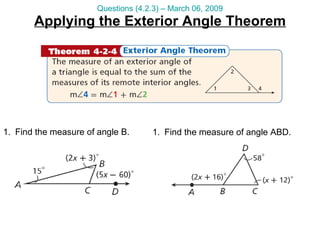
The document contains math tutorial questions and solutions about classifying triangles, finding angle measures in triangles, and applying the exterior angle theorem. It includes questions such as calculating the number of triangles that can be made from a given length of steel beam, finding missing angle measures in triangles using properties of angles sums, and determining angle measures using the exterior angle theorem.

1. Math Tutorial Questions For the week of February 02 – February 06 ***No Lesson for March 3 (ELA TAKS Testing)

2. Classifying Triangles—Application Questions (4.1.4) – March 02, 2009 A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? A jeweler creates triangular earrings by bending pieces of silver wire. Each earring is an isosceles triangle with legs of 3 cm and a base of 1.5 cm. How many earring can be made from a piece of wire that is 50 cm long?

3. Classifying Triangles—Application Solutions (4.1.4) – March 02, 2009 A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? In an equilateral triangle all sides are equal, so in this situation all sides of the triangle are 18 feet long. The perimeter of one triangle: 3 x 18 feet = 54 feet To find # of triangles that can be formed out of 420 feet of steel beam: 420 feet / 54 feet = 7.78 It is not possible to make part of a beam, so only 7 complete beams can be made. A jeweler creates triangular earrings by bending pieces of silver wire. Each earring is an isosceles triangle with legs of 3 cm and a base of 1.5 cm. How many earring can be made from a piece of wire that is 50 cm long? In an isosceles triangle the 2 legs are the same length and the base is different, so in this situation there are 2 sides with a length of 3 cm and on with a length of 1.5 cm. The perimeter of one triangle: (2 x 3 cm) + 1.5 cm = 7.5 cm To find # of earring that can be formed out of 50 cm of wire: 50 cm / 7.5 cm = 6.67 It is not possible to make part of an earring, so only 6 complete earrings can be made. 18 ft 18 ft 18 ft 2 cm 2 cm 2 cm

4. Angle Relationships in Triangles—Application Questions (4.2.1) – March 04, 2009 After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find the indicated angle measures. Measure of Angle XYZ Measure of Angle YWZ The diagram is a map showing John’s house, Kay’s house and the grocery store. What is the angle the two houses make with the store?

5. Angle Relationships in Triangles—Application Solutions (4.2.1) – March 04, 2009 After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find the indicated angle measures. Measure of Angle XYZ Measure of Angle YWZ The diagram is a map showing John’s house, Kay’s house and the grocery store. What is the angle the two houses make with the store? Δ XYZ: 62º + 40º + Angle XYZ = 180º (Use Triangle Sum Theorem) 102º + Angle XYZ = 180º (Add 62 & 40) Angle XYZ = 78º (Subtract 102 from both sides of equation) Δ YWZ: (12 + 78)º + 40º + Angle YWZ = 180º (Use Triangle Sum Theorem) 130º + Angle YWZ = 180º (Add 12, 78, & 40) Angle XYZ = 50º (Subtract 130 from both sides of equation) 78º (8y + 10)º + (y + 32)º + (2y + 6)º= 180º (Use Triangle Sum Theorem) (11y + 48)º = 180º (Add 8y, y & 2y; Add 10, 32, & 6) (11y)º = 132º (Subtract 48 from both sides of equation) y = 12 (Divide both sides by 11) Angle of store with 2 houses = 2y + 6 = 2(12) + 6 (Substitute 12 in for y) = 30 º (Multiply 2 & 12, then add 6)

6. Finding Angle Measures in Right Triangles Questions (4.2.2) – March 05, 2009 The measure of one of the acute angles in a right triangle is given. What is the measure of the other acute angle? 20.8º 2xº 56 ½ º

7. Finding Angle Measures in Right Triangles Solutions (4.2.2) – March 05, 2009 The measure of one of the acute angles in a right triangle is given. What is the measure of the other acute angle? 20.8º (y = other acute angle) 20.8º + yº = 90º (Corollary 4-2-2) y = 69.2º (Subtract 20.8 from both sides of equation) 2xº (y = other acute angle) 2xº + yº = 90º (Corollary 4-2-2) y = (90 – 2x)º (Subtract 2x from both sides of equation; leave as equation) 56 ½ º (y = other acute angle) 56 ½ º + yº = 90º (Corollary 4-2-2) y = 33 ½ º (Subtract 56 ½ from both sides of equation)

8. Applying the Exterior Angle Theorem Questions (4.2.3) – March 06, 2009 Find the measure of angle B. Find the measure of angle ABD.

9. Applying the Exterior Angle Theorem Solutions (4.2.3) – March 06, 2009 Find the measure of angle B. Find the measure of angle ABD. 15º + (2x + 3)º = (5x – 60)º (Exterior Angle Theorem) 2x + 18 = 5x – 60 (Add 15 & 3) 18 = 3x – 60 (Subtract 2x from both sides of equation) 78 = 3x (Add 60 to both sides of equation) x = 26 (Divide both sides of equation by 3) Angle B = 2x + 3 Angle B = 2(26) + 3 (Substitute 26 in for x) Angle B = 52 + 3 (Multiply 2 & 26) Angle B = 58º (Add 52 & 3) 58º + (x + 12)º = (2x + 16)º (Exterior Angle Theorem) x + 70 = 2x + 16 (Add 58 & 12) 70 = x + 16 (Subtract x from both sides of equation) 54 = x (Subtract 16 from both sides of equation) Angle ABD = 2x + 16 Angle ABD = 2(54) + 16 (Substitute 54 in for x) Angle ABD = 108 + 16 (Multiply 2 & 54) Angle ABD = 124º (Add 108 & 16)