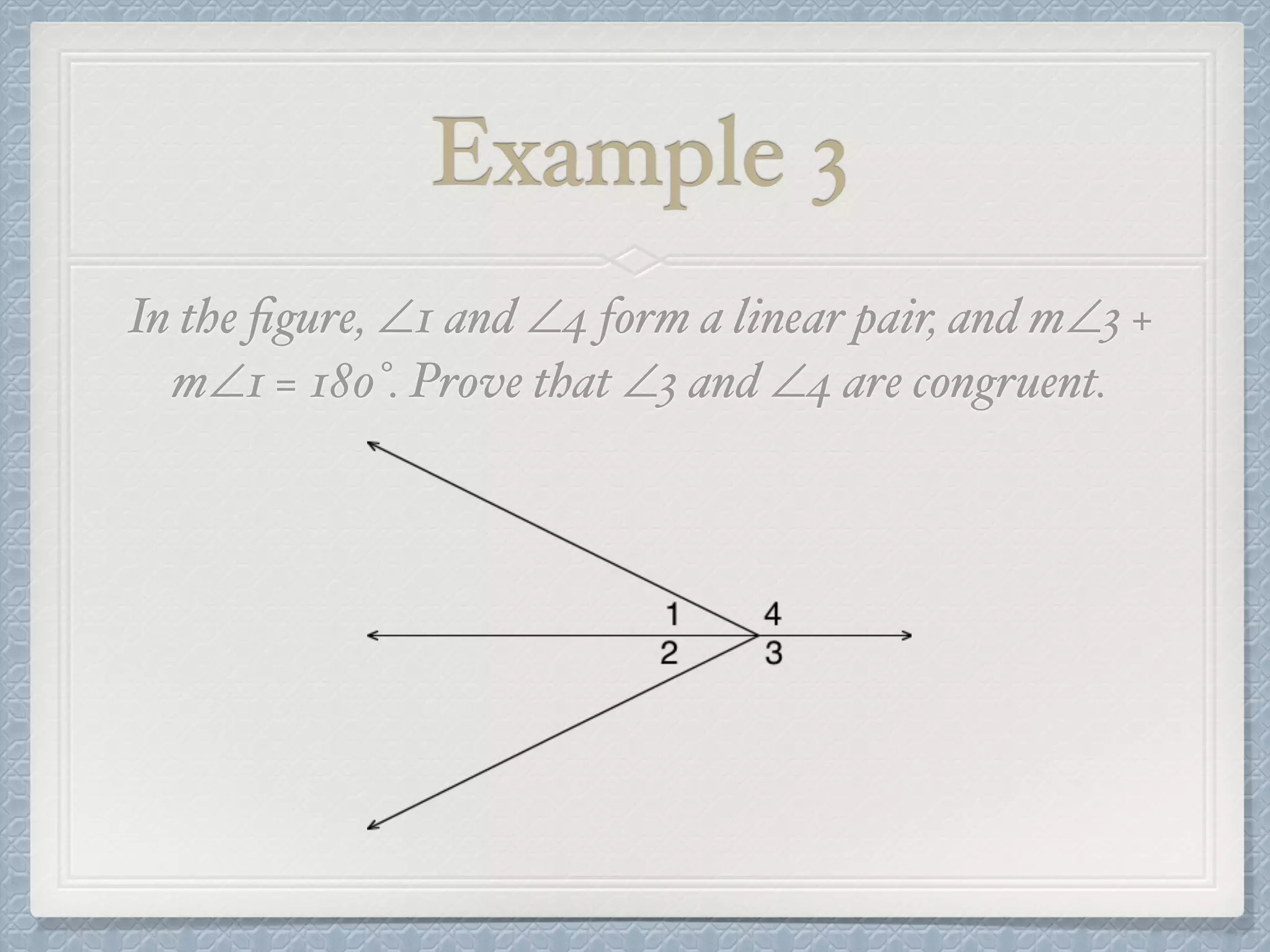
This document discusses various postulates and theorems about angle relationships. It defines supplementary and complementary angles and discusses properties of congruent angles. It also covers theorems about right angles and perpendicular lines. Examples are provided to illustrate using these concepts to prove angle congruence and find missing angle measures.

1. Section 2-6
ProvingAngle Relationships

2. Essential Questions
How do you write proofs involving supplementary and
complementary angles?
How do you write proofs involving congruent and
right angles?

3. More Postulates and Theorems
Protractor Postulate:
AngleAddition Postulate:
Supplement Theorem:

4. More Postulates and Theorems
Protractor Postulate: Given any angle, the measure
can be put into one-to-one correspondence with
real numbers between 0 and 180
AngleAddition Postulate:
Supplement Theorem:

5. More Postulates and Theorems
Protractor Postulate: Given any angle, the measure
can be put into one-to-one correspondence with
real numbers between 0 and 180
This means we can measure angles in degrees
AngleAddition Postulate:
Supplement Theorem:

6. More Postulates and Theorems
Protractor Postulate: Given any angle, the measure
can be put into one-to-one correspondence with
real numbers between 0 and 180
This means we can measure angles in degrees
AngleAddition Postulate: D is in the interior of ∠ABC
IFF m∠ABD + m∠DBC = m∠ABC
Supplement Theorem:

7. More Postulates and Theorems
Protractor Postulate: Given any angle, the measure
can be put into one-to-one correspondence with
real numbers between 0 and 180
This means we can measure angles in degrees
AngleAddition Postulate: D is in the interior of ∠ABC
IFF m∠ABD + m∠DBC = m∠ABC
Supplement Theorem:If two angles form a linear pair,
then they are supplementary angles

8. More Postulates and Theorems
Complement Theorem:
Properties ofAngle Congruence
Reflexive Property of Congruence:
Symmetric Property of Congruence:
Transitive Property of Congruence:

9. More Postulates and Theorems
Complement Theorem:If the non-common sides of two
adjacent angles form a right angle, then the angles
are complementary angles
Properties ofAngle Congruence
Reflexive Property of Congruence:
Symmetric Property of Congruence:
Transitive Property of Congruence:

10. More Postulates and Theorems
Complement Theorem:If the non-common sides of two
adjacent angles form a right angle, then the angles
are complementary angles
Properties ofAngle Congruence
Reflexive Property of Congruence: ∠1 ≅ ∠1
Symmetric Property of Congruence:
Transitive Property of Congruence:

11. More Postulates and Theorems
Complement Theorem:If the non-common sides of two
adjacent angles form a right angle, then the angles
are complementary angles
Properties ofAngle Congruence
Reflexive Property of Congruence: ∠1 ≅ ∠1
Symmetric Property of Congruence:
If ∠1 ≅ ∠2, then ∠2 ≅ ∠1
Transitive Property of Congruence:

12. More Postulates and Theorems
Complement Theorem:If the non-common sides of two
adjacent angles form a right angle, then the angles
are complementary angles
Properties ofAngle Congruence
Reflexive Property of Congruence: ∠1 ≅ ∠1
Symmetric Property of Congruence:
If ∠1 ≅ ∠2, then ∠2 ≅ ∠1
Transitive Property of Congruence:
If ∠1 ≅ ∠2 and ∠2 ≅ ∠3, then ∠1 ≅ ∠3

13. More Postulates and Theorems
Congruent Supplements Theorem:
Congruent Complements Theorem:
VerticalAngles Theorem:

14. More Postulates and Theorems
Congruent Supplements Theorem:Angles
supplementary to the same angle or
supplementary to congruent angles are congruent
Congruent Complements Theorem:
VerticalAngles Theorem:

15. More Postulates and Theorems
Congruent Supplements Theorem:Angles
supplementary to the same angle or
supplementary to congruent angles are congruent
Congruent Complements Theorem: Angles
complementary to the same angle or
complementary to congruent angles are congruent
VerticalAngles Theorem:

16. More Postulates and Theorems
Congruent Supplements Theorem:Angles
supplementary to the same angle or
supplementary to congruent angles are congruent
Congruent Complements Theorem: Angles
complementary to the same angle or
complementary to congruent angles are congruent
VerticalAngles Theorem: If two angles are vertical
angles, then they are congruent

17. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9:
Theorem 2.10:
Theorem 2.11:
Theorem 2.12:
Theorem 2.13:

18. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9: Perpendicular lines intersect to form
four right angles
Theorem 2.10:
Theorem 2.11:
Theorem 2.12:
Theorem 2.13:

19. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9: Perpendicular lines intersect to form
four right angles
Theorem 2.10:All right angles are congruent
Theorem 2.11:
Theorem 2.12:
Theorem 2.13:

20. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9: Perpendicular lines intersect to form
four right angles
Theorem 2.10:All right angles are congruent
Theorem 2.11: Perpendicular lines form congruent
adjacent angles
Theorem 2.12:
Theorem 2.13:

21. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9: Perpendicular lines intersect to form
four right angles
Theorem 2.10:All right angles are congruent
Theorem 2.11: Perpendicular lines form congruent
adjacent angles
Theorem 2.12:If two angles are congruent and
supplementary, then each angle is a right angle
Theorem 2.13:

22. EVEN
More Postulates and Theorems
RightAngle Theorems
Theorem 2.9: Perpendicular lines intersect to form
four right angles
Theorem 2.10:All right angles are congruent
Theorem 2.11: Perpendicular lines form congruent
adjacent angles
Theorem 2.12:If two angles are congruent and
supplementary, then each angle is a right angle
Theorem 2.13: If two congruent angles form a linear
pair, then they are right angles

23. Example 1
Using a protractor, a construction worker measures that the
angle a beam makes with the ceiling is 42°. What is the
measure of the angle that the beam makes with the wall?

24. Example 1
Using a protractor, a construction worker measures that the
angle a beam makes with the ceiling is 42°. What is the
measure of the angle that the beam makes with the wall?
Ceiling
Wall
Beam
42°

25. Example 1
Using a protractor, a construction worker measures that the
angle a beam makes with the ceiling is 42°. What is the
measure of the angle that the beam makes with the wall?
Ceiling
Wall
Beam
42°
90°-42°

26. Example 1
Using a protractor, a construction worker measures that the
angle a beam makes with the ceiling is 42°. What is the
measure of the angle that the beam makes with the wall?
Ceiling
Wall
Beam
42°
90°-42°
48°

27. Example 2
At 4:00 on an analog clock, the angle between the hour and
minute hands of a clock is 120°. When the second hand
bisects the angle between the hour and minute hands, what
are the measures of the angles between the minute and
second hands and between the second and the hour hands?

28. Example 2
At 4:00 on an analog clock, the angle between the hour and
minute hands of a clock is 120°. When the second hand
bisects the angle between the hour and minute hands, what
are the measures of the angles between the minute and
second hands and between the second and the hour hands?
Since the larger angle of 120° is bisected, two smaller
angles of 60° are formed, and since those two angles
add up to the larger one, both angles we are looking
for have a measure of 60°.

29. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.

30. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.

31. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°

32. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given

33. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary

34. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary
Linear pairs are
supplementary

35. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary
Linear pairs are
supplementary
∠3 and ∠1 are supplementary

36. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary
Linear pairs are
supplementary
∠3 and ∠1 are supplementary
Def. of
supplementary

37. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary
Linear pairs are
supplementary
∠3 and ∠1 are supplementary
Def. of
supplementary
∠3 ≅ ∠4

38. Example 3
In the figure, ∠1 and ∠4 form a linear pair, and m∠3 +
m∠1 = 180°. Prove that ∠3 and ∠4 are congruent.
∠1 and ∠4 form a linear pair,
and m∠3 + m∠1 = 180°
Given
∠1 and ∠4 are supplementary
Linear pairs are
supplementary
∠3 and ∠1 are supplementary
Def. of
supplementary
∠3 ≅ ∠4 Angles supplementary to same ∠ are ≅