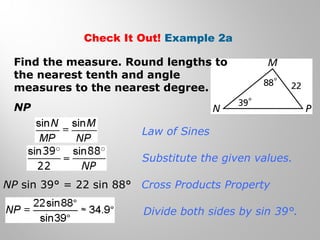
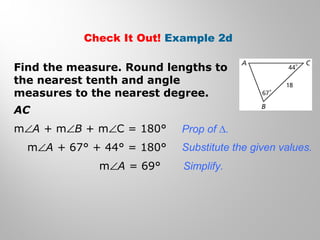
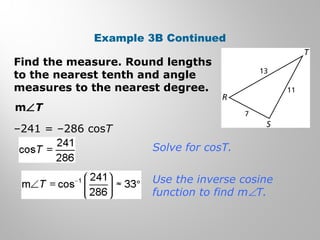
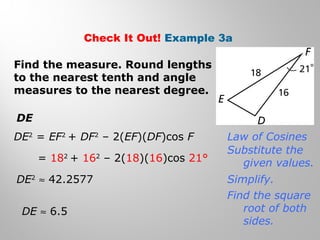
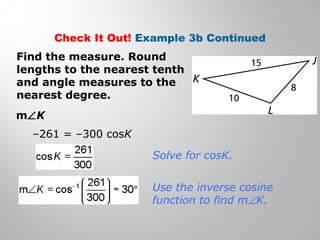
This document provides examples and explanations for using the Law of Sines and Law of Cosines to solve triangles. It begins with examples of finding trigonometric ratios for angles up to 180 degrees. It then shows how to use the Law of Sines to find missing side lengths or angle measures when given two angles and a side, or two sides and a non-included angle. The Law of Cosines is demonstrated for finding a missing side or angle when given two sides and the included angle, or all three sides. Multiple practice problems are provided to help understand applying these laws.

1. UUNNIITT 88..55 LLAAWW OOFF SSIINNEESS
AANNDD CCOOSSIINNEESS

2. Warm Up
1. What is the third angle measure in a triangle with
angles measuring 65° and 43°?
72°
Find each value. Round trigonometric
ratios to the nearest hundredth and angle
measures to the nearest degree.
2. sin 73° 3. cos 18° 4. tan 82°
0.96 0.95 7.12
5. sin-1 (0.34) 6. cos-1 (0.63) 7. tan-1 (2.75)
20° 51° 70°

3. Objective
Use the Law of Sines and the Law of
Cosines to solve triangles.

4. In this lesson, you will learn to solve any triangle.
To do so, you will need to calculate trigonometric
ratios for angle measures up to 180°. You can use a
calculator to find these values.

5. Example 1: Finding Trigonometric Ratios for Obtuse
Angles
Use your calculator to find each trigonometric
ratio. Round to the nearest hundredth.
A. tan 103° B. cos 165° C. sin 93°
tan 103° » –4.33 cos 165° » –0.97 sin 93° » 1.00

6. Check It Out! Example 1
Use a calculator to find each trigonometric
ratio. Round to the nearest hundredth.
a. tan 175°
tan 175° » –0.09
b. cos 92° c. sin 160°
cos 92° » –0.03 sin 160° » 0.34

7. You can use the altitude of a triangle to find a
relationship between the triangle’s side lengths.
In ΔABC, let h represent the length of
the altitude from C to
From the diagram, ,
and
By solving for h, you find that h = b sin A and h = a
sin B. So b sin A = a sin B, and .
You can use another altitude to show that these
ratios equal

8. You can use the Law of Sines to solve a triangle if you
are given
• two angle measures and any side length
(ASA or AAS) or
• two side lengths and a non-included angle measure
(SSA).

9. Example 2A: Using the Law of Sines
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
FG
Law of Sines
Substitute the given values.
Cross Products Property
Divide both sides by sin 39°.
FG sin 39° = 40 sin 32°

10. Example 2B: Using the Law of Sines
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
mÐQ
Law of Sines
Substitute the given
values.
Multiply both sides by 6.
Use the inverse sine function
to find mÐQ.

11. Check It Out! Example 2a
Find the measure. Round lengths to
the nearest tenth and angle
measures to the nearest degree.
NP
Law of Sines
Substitute the given values.
Cross Products Property
Divide both sides by sin 39°.
NP sin 39° = 22 sin 88°

12. Check It Out! Example 2b
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
mÐL
Law of Sines
Substitute the given values.
Cross Products Property
Use the inverse sine
function to find mÐL.
10 sin L = 6 sin 125°

13. Check It Out! Example 2c
Find the measure. Round lengths to
the nearest tenth and angle
measures to the nearest degree.
mÐX
Law of Sines
Substitute the given values.
Cross Products Property
Use the inverse sine
function to find mÐX.
7.6 sin X = 4.3 sin 50°

14. Check It Out! Example 2d
Find the measure. Round lengths to
the nearest tenth and angle
measures to the nearest degree.
AC
mÐA + mÐB + mÐC = 180°
mÐA + 67° + 44° = 180°
mÐA = 69°
Prop of Δ.
Substitute the given values.
Simplify.

15. Check It Out! Example 2D Continued
Find the measure. Round lengths to
the nearest tenth and angle
measures to the nearest degree.
Law of Sines
Substitute the given values.
Cross Products Property
Divide both sides by sin 69°.
AC sin 69° = 18 sin 67°

16. The Law of Sines cannot be used to solve every
triangle. If you know two side lengths and the
included angle measure or if you know all three side
lengths, you cannot use the Law of Sines. Instead,
you can apply the Law of Cosines.

17. You can use the Law of Cosines to solve a triangle if
you are given
• two side lengths and the included angle measure
(SAS) or
• three side lengths (SSS).

18. Helpful Hint
The angle referenced in the Law of Cosines is
across the equal sign from its corresponding side.

19. Example 3A: Using the Law of Cosines
Find the measure. Round
lengths to the nearest tenth
and angle measures to the
nearest degree.
XZ
XZ2 = XY2 + YZ2 – 2(XY)(YZ)cos Y
= 352 + 302 – 2(35)(30)cos 110°
XZ2 » 2843.2423
XZ » 53.3
Law of Cosines
Substitute the
given values.
Simplify.
Find the square
root of both
sides.

20. Example 3B: Using the Law of Cosines
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
mÐT
RS2 = RT2 + ST2 – 2(RT)(ST)cos T
72 = 132 + 112 – 2(13)(11)cos T
49 = 290 – 286 cosT
–241 = –286 cosT
Law of Cosines
Substitute the
given values.
Simplify.
Subtract 290
both sides.

21. Example 3B Continued
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
mÐT
–241 = –286 cosT
Solve for cosT.
Use the inverse cosine
function to find mÐT.

22. Check It Out! Example 3a
Find the measure. Round lengths
to the nearest tenth and angle
measures to the nearest degree.
DE
DE2 = EF2 + DF2 – 2(EF)(DF)cos F
= 182 + 162 – 2(18)(16)cos 21°
DE2 » 42.2577
DE » 6.5
Law of Cosines
Substitute the
given values.
Simplify.
Find the square
root of both
sides.

23. Check It Out! Example 3b
Find the measure. Round
lengths to the nearest tenth
and angle measures to the
nearest degree.
mÐK
JL2 = LK2 + KJ2 – 2(LK)(KJ)cos K
82 = 152 + 102 – 2(15)(10)cos K
64 = 325 – 300 cosK
–261 = –300 cosK
Law of Cosines
Substitute the
given values.
Simplify.
Subtract 325
both sides.

24. Check It Out! Example 3b Continued
Find the measure. Round
lengths to the nearest tenth
and angle measures to the
nearest degree.
mÐK
–261 = –300 cosK
Solve for cosK.
Use the inverse cosine
function to find mÐK.

25. Check It Out! Example 3c
Find the measure. Round
lengths to the nearest tenth
and angle measures to the
nearest degree.
YZ
YZ2 = XY2 + XZ2 – 2(XY)(XZ)cos X
= 102 + 42 – 2(10)(4)cos 34°
YZ2 » 49.6770
YZ » 7.0
Law of Cosines
Substitute the
given values.
Simplify.
Find the square
root of both
sides.

26. Check It Out! Example 3d
Find the measure. Round
lengths to the nearest tenth and
angle measures to the nearest
degree.
mÐR
PQ2 = PR2 + RQ2 – 2(PR)(RQ)cos R
9.62 = 5.92 + 10.52 – 2(5.9)(10.5)cos R
92.16 = 145.06 – 123.9cosR
–52.9 = –123.9 cosR
Law of Cosines
Substitute the
given values.
Simplify.
Subtract 145.06
both sides.

27. Check It Out! Example 3d Continued
Find the measure. Round
lengths to the nearest tenth and
angle measures to the nearest
degree.
mÐR
–52.9 = –123.9 cosR
Solve for cosR.
Use the inverse cosine
function to find mÐR.

28. Helpful Hint
Do not round your answer until the final step of
the computation. If a problem has multiple steps,
store the calculated answers to each part in your
calculator.

29. Example 4: Sailing Application
A sailing club has planned a
triangular racecourse, as shown in
the diagram. How long is the leg of
the race along BC? How many
degrees must competitors turn at
point C? Round the length to the
nearest tenth and the angle
measure to the nearest degree.

30. Example 4 Continued
Step 1 Find BC.
BC2 = AB2 + AC2 – 2(AB)(AC)cos A
= 3.92 + 3.12 – 2(3.9)(3.1)cos 45°
BC2 » 7.7222
BC » 2.8 mi
Law of Cosines
Substitute the
given values.
Simplify.
Find the square
root of both
sides.

31. Example 4 Continued
Step 2 Find the measure of the angle through which
competitors must turn. This is mÐC.
Law of Sines
Substitute the
given values.
Multiply both sides
by 3.9.
Use the inverse
sine function to
find mÐC.

32. Check It Out! Example 4
What if…? Another engineer suggested using a
cable attached from the top of the tower to a
point 31 m from the base. How long would this
cable be, and what angle would it make with
the ground? Round the length to the nearest
tenth and the angle measure to the nearest
degree.
31 m

33. Check It Out! Example 4 Continued
Step 1 Find the length of the cable.
AC2 = AB2 + BC2 – 2(AB)(BC)cos B
= 312 + 562 – 2(31)(56)cos 100°
AC2 » 4699.9065
AC »68.6 m
Law of Cosines
Substitute the
given values.
Simplify.
Find the square
root of both
sides.

34. Check It Out! Example 4 Continued
Step 2 Find the measure of the angle the cable would
make with the ground.
Law of Sines
Substitute the
given values.
Multiply both sides
by 56.
Use the inverse
sine function to
find mÐA.

35. Lesson Quiz: Part I
Use a calculator to find each trigonometric
ratio. Round to the nearest hundredth.
1. tan 154°
–0.49
2. cos 124°
–0.56
3. sin 162°
0.31

36. Lesson Quiz: Part II
Use ΔABC for Items 4–6. Round lengths to
the nearest tenth and angle measures to the
nearest degree.
4. mÐB = 20°, mÐC = 31° and b = 210. Find a.
5. a = 16, b = 10, and mÐC = 110°. Find c.
6. a = 20, b = 15, and c = 8.3. Find mÐA.
477.2
21.6
115°

37. Lesson Quiz: Part III
7. An observer in tower A sees a fire 1554 ft away at
an angle of depression of 28°. To the nearest
foot, how far is the fire from an observer in tower
B? To the nearest degree, what is the angle of
depression to the fire from tower B?
1212 ft; 37°

38. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the Copyright Act
1976, allowance is made for
"fair use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by
copyright statute that might
otherwise be infringing.
Non-profit, EDUCATIONAL or
personal use tips the balance in
favor of fair use.