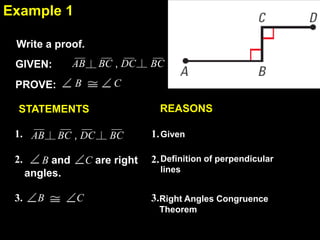
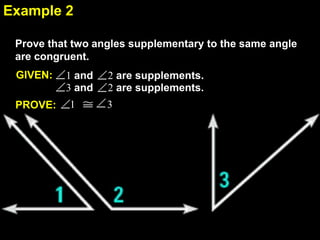
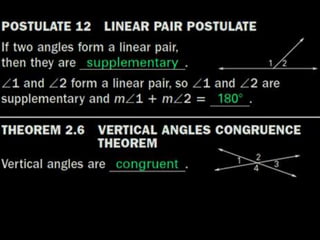
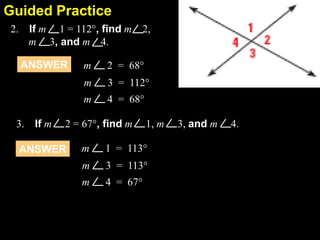
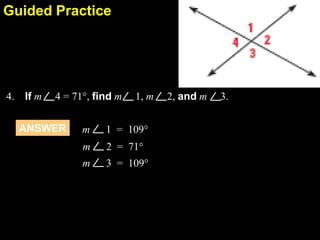
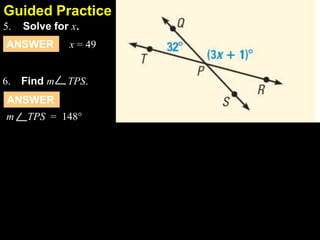
This document contains examples and explanations of angle pair relationships and angle proofs. It begins with definitions of equal angles if they are both right angles, angles formed by perpendicular lines, and congruent segment angles. Several examples of angle proofs are provided using statements and reasons. Guided practice problems ask to find missing angle measures using angle relationships. The document concludes with an exit slip and homework assignment.

1. 2.72.7 Prove Angle Pair Relationships
Bell Thinger
Give a reason for each statement.
ANSWER Transitive Prop. of Eq.
ANSWER Def. of perpendicular
ANSWER Def. of segment congruence
1. If m 1 = 90º and m 2 = 90º, then m 1 = m 2.
2. If AB BC , then ABC is a right angle.┴
3. If FG RS, then FG = RS=

2. 2.7

3. 2.7Example 1
STATEMENTS REASONS
1.Given1. AB BC , DC BC
2.Definition of perpendicular
lines
2. B and C are right
angles.
Write a proof.
GIVEN: AB BC , DC BC
PROVE: B C
3.Right Angles Congruence
Theorem
3. B C

4. 2.7

5. 2.7Example 2
Prove that two angles supplementary to the same angle
are congruent.
GIVEN: 1 and 2 are supplements.
3 and 2 are supplements.
PROVE: 1 3

6. 2.7
STATEMENTS REASONS
Given1.
Example 2
2. m 1+ m 2 = 180°
m 3+ m 2 = 180°
2. Definition of
supplementary angles
Transitive Property of
Equality
3.3. m 1 + m 2 = m 3 + m 2
4. m 1 = m 3 Subtraction
Property of Equality
4.
5. 1 3 Definition of
congruent angles
5.
1 and 2 are supplements.1.
3 and 2 are supplements.

7. 2.7

8. 2.7Example 3
GIVEN: 5 and 7 are vertical angles.
PROVE: 5 7
Prove vertical angles are congruent.
STATEMENTS REASONS
5 and 7 are vertical angles.1. 1. Given
2. 5 and 6 are a linear pair.
6 and 7 are a linear pair.
2. Definition of linear
pair, as shown in the
diagram
3. 5 and 6 are supplementary.
6 and 7 are supplementary.
3. Linear Pair Postulate
4. 5 7 Congruent
Supplements Theorem
4.

9. 2.7Guided Practice
2. If m 1 = 112°, find m 2,
m 3, and m 4.
ANSWER m 2 = 68°
m 3 = 112°
m 4 = 68°
3. If m 2 = 67°, find m 1, m 3, and m 4.
ANSWER m 1 = 113°
m 3 = 113°
m 4 = 67°

10. 2.7Guided Practice
4. If m 4 = 71°, find m 1, m 2, and m 3.
ANSWER m 1 = 109°
m 2 = 71°
m 3 = 109°

11. 2.7Example 4
SOLUTION
Because TPQ and QPR form a linear pair, the sum
of their measures is 180.
The correct answer is B.
ANSWER

12. 2.7Example 5
Tell whether the proof is logically valid.
If it is not, explain how to change the
proof so that it is valid.
GIVEN: 1 is a right angle.
PROVE: 3 is a right angle.
STATEMENTS REASONS
1. 1 is a right angle. 1. Given
3. 3 is a right angle. 3. Right Angles
Congruence Theorem
2. 1 3 2. Vertical Angles
Congruence Theorem

13. 2.7
The proof is not logically valid. The Right Angles
Congruence Theorem does not let you conclude that
3 is a right angle. It just says that all right angles are
congruent.
Here is a way to complete the proof.
SOLUTION
Example 5

14. 2.7
REASONSSTATEMENTS
6. 3 is a right angle.
1. 1 is a right angle.
2. 1 3
1. Given
2. Vertical Angles
Congruence Theorem
3. Definition of congruent
angles
3. m 1 = m 3
4. m 1 = 90º
5. m 3 = 90º
4. Definition of right angle
5. Transitive Property of
Equality
6. Definition of right angle
Example 5

15. 2.7Guided Practice
5. Solve for x.
x = 49ANSWER
6. Find m TPS.
m TPS = 148°
ANSWER

16. 2.7Exit Slip
1. Give the reason for each step
Def. of linear pair
Given
PROVE : 1is supplementary to 4
GIVEN : 1 5
Substitution Prop. of Eq.
Def. of supplementary
Linear Pair Post .
Def. of supplementary
STATEMENTS REASONS
2. m 1 = m 5
3. 4 and are a linear pair.5
1. 1 5
4 and are supplementary .4. 5
m 4 + m 5 = 1805.
m 4 + m 1 = 1806.
7. 1 is supplementary to 4.
Def. of

17. 2.7
Homework
Pg 129-133
# 10, 14, 28, 37, 38