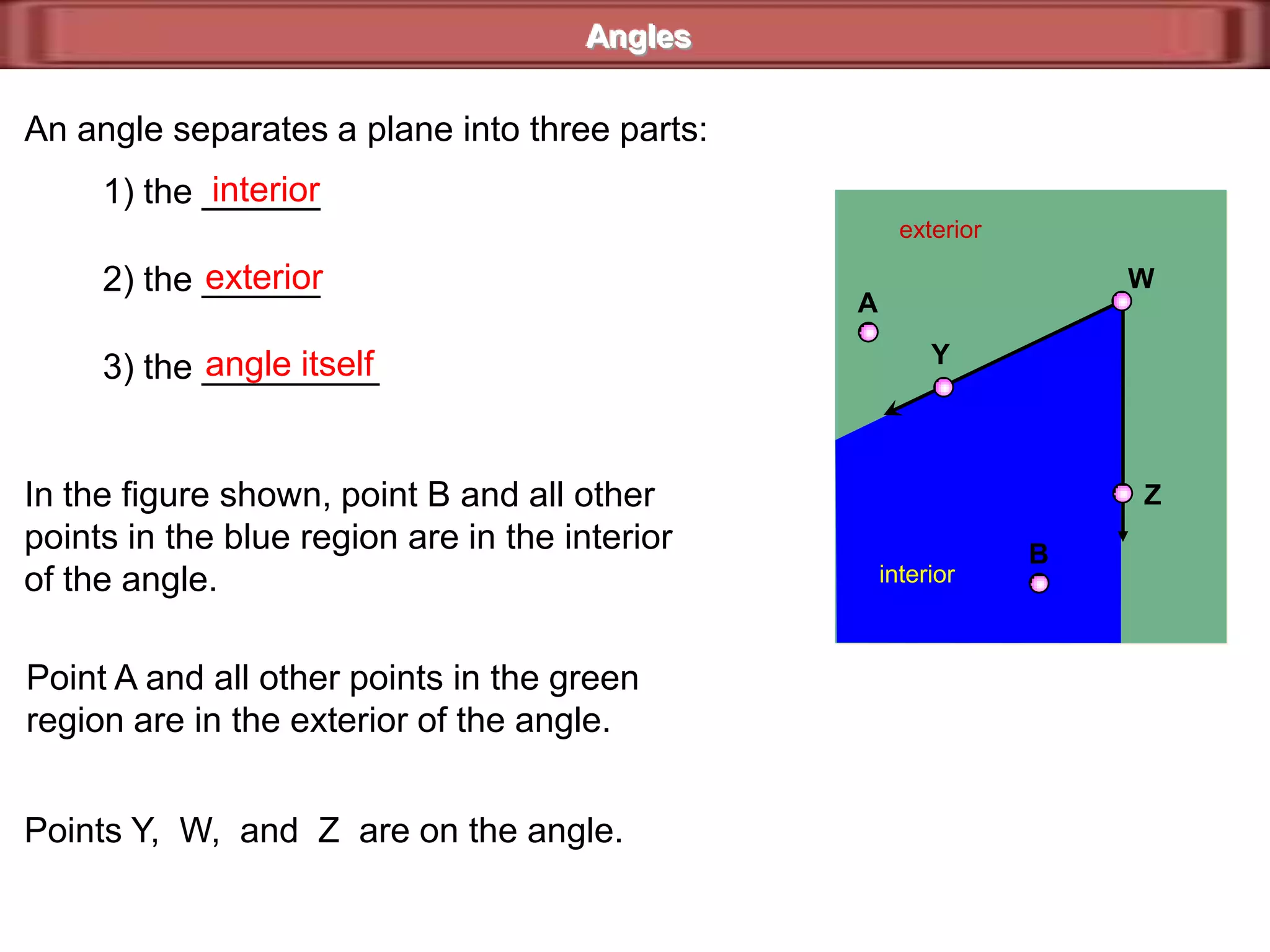
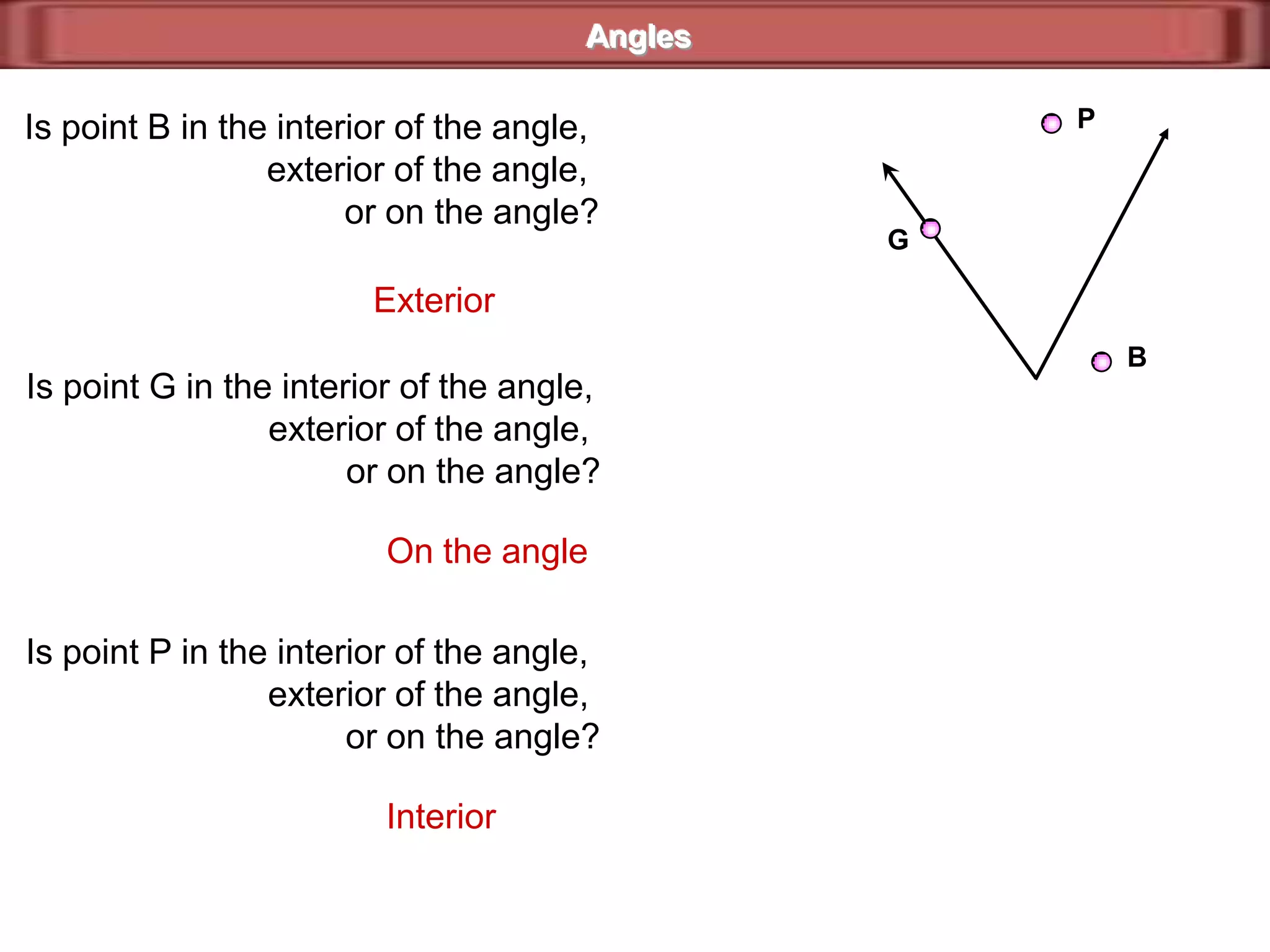
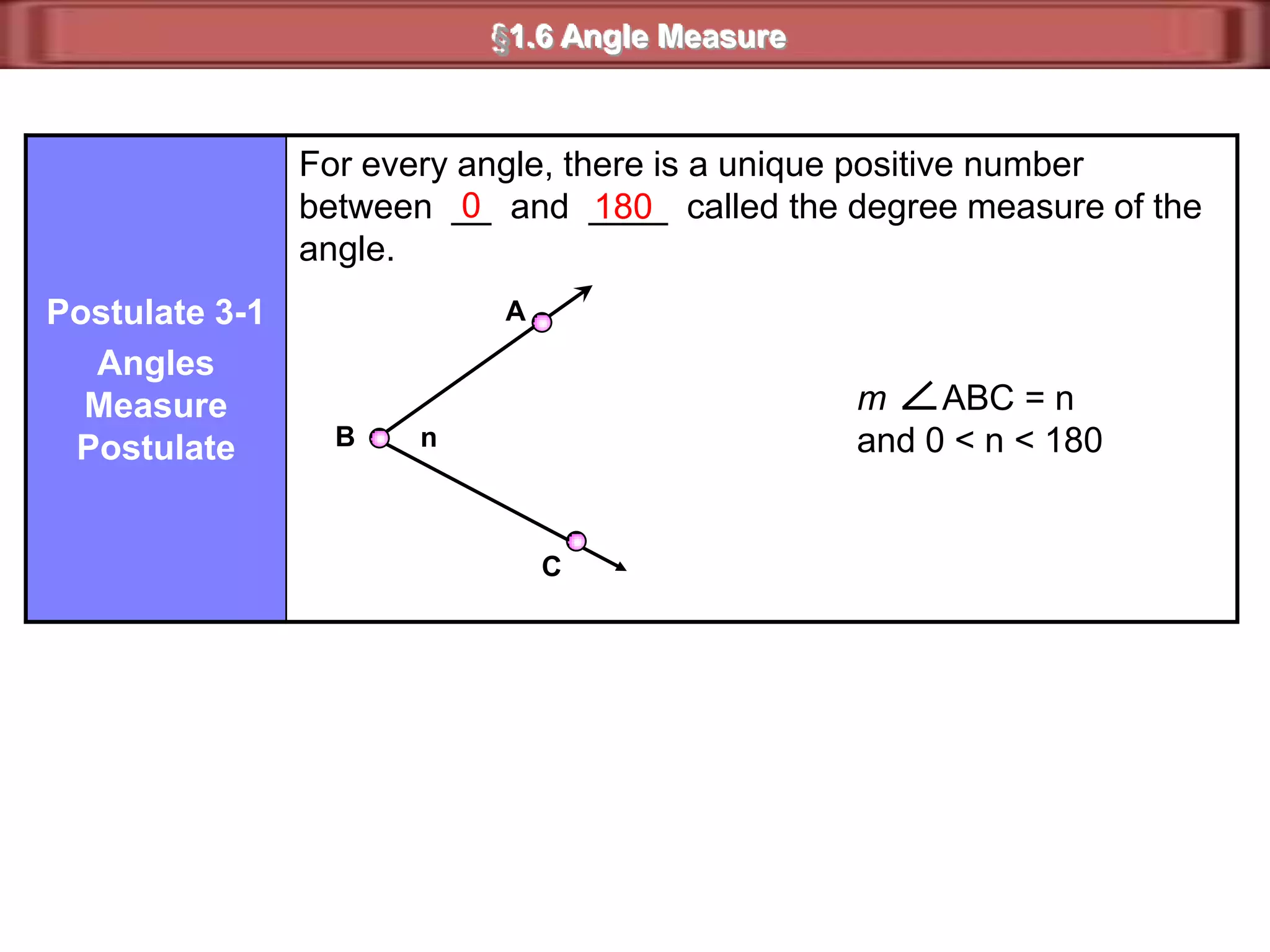
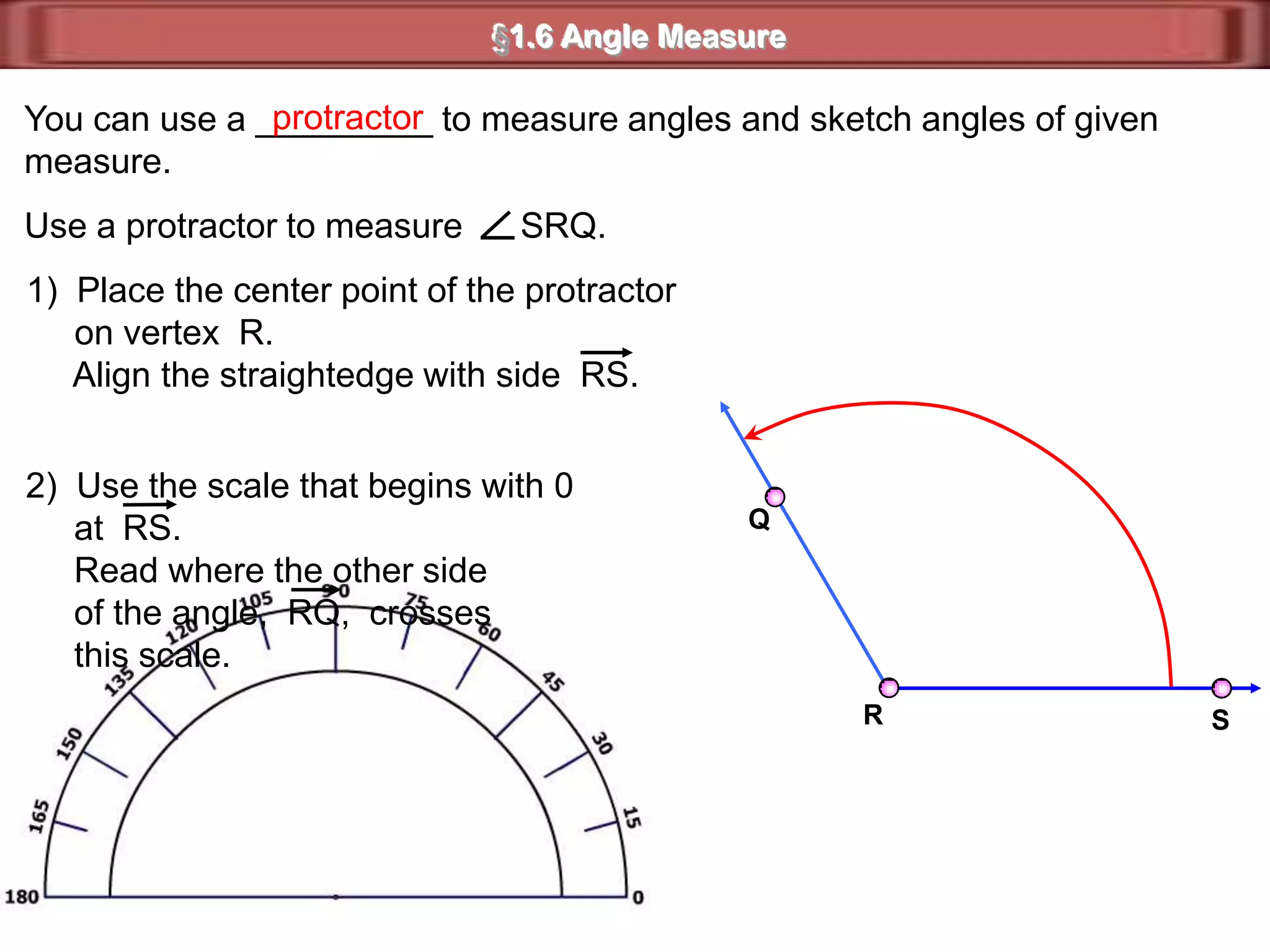
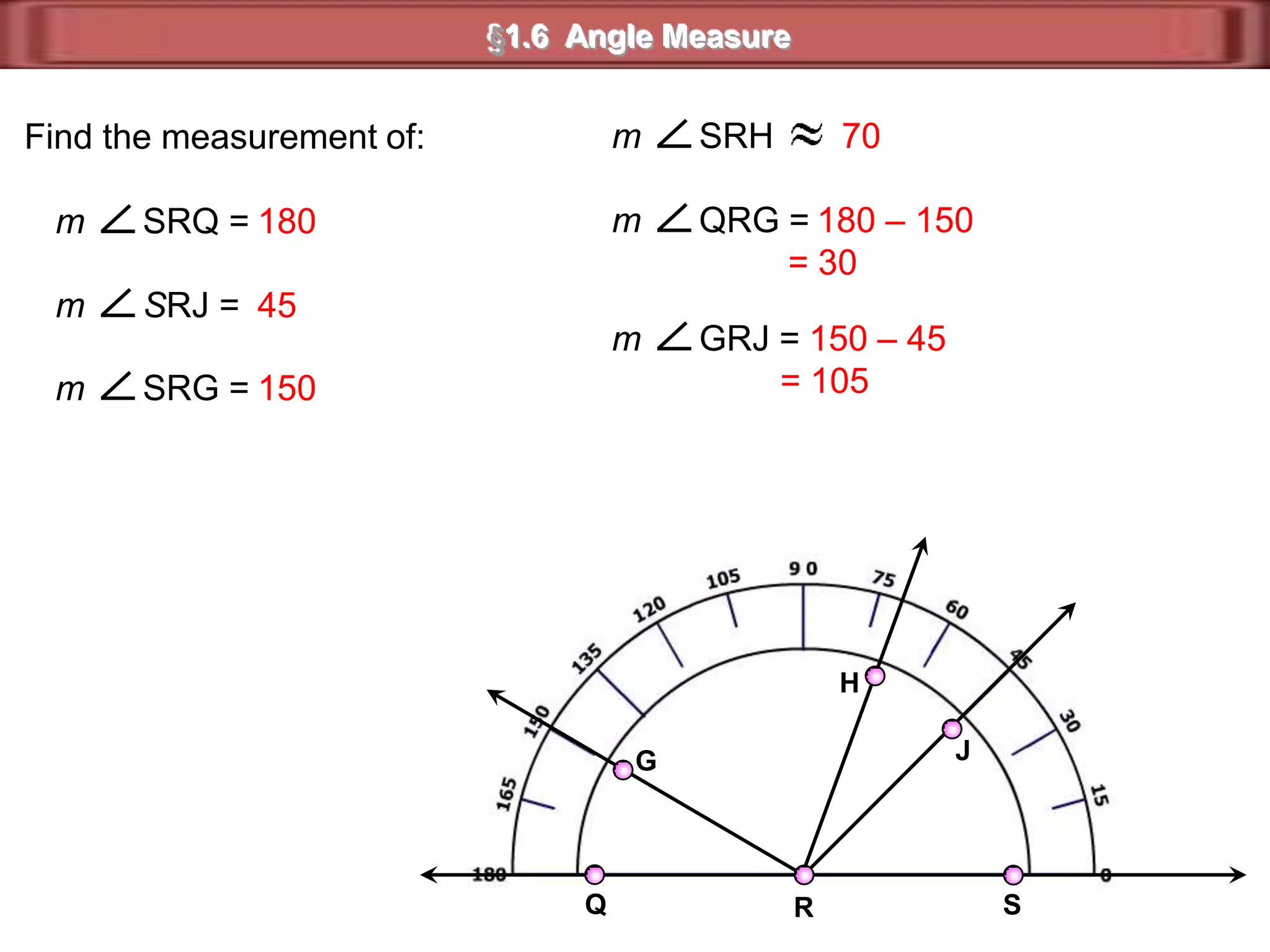
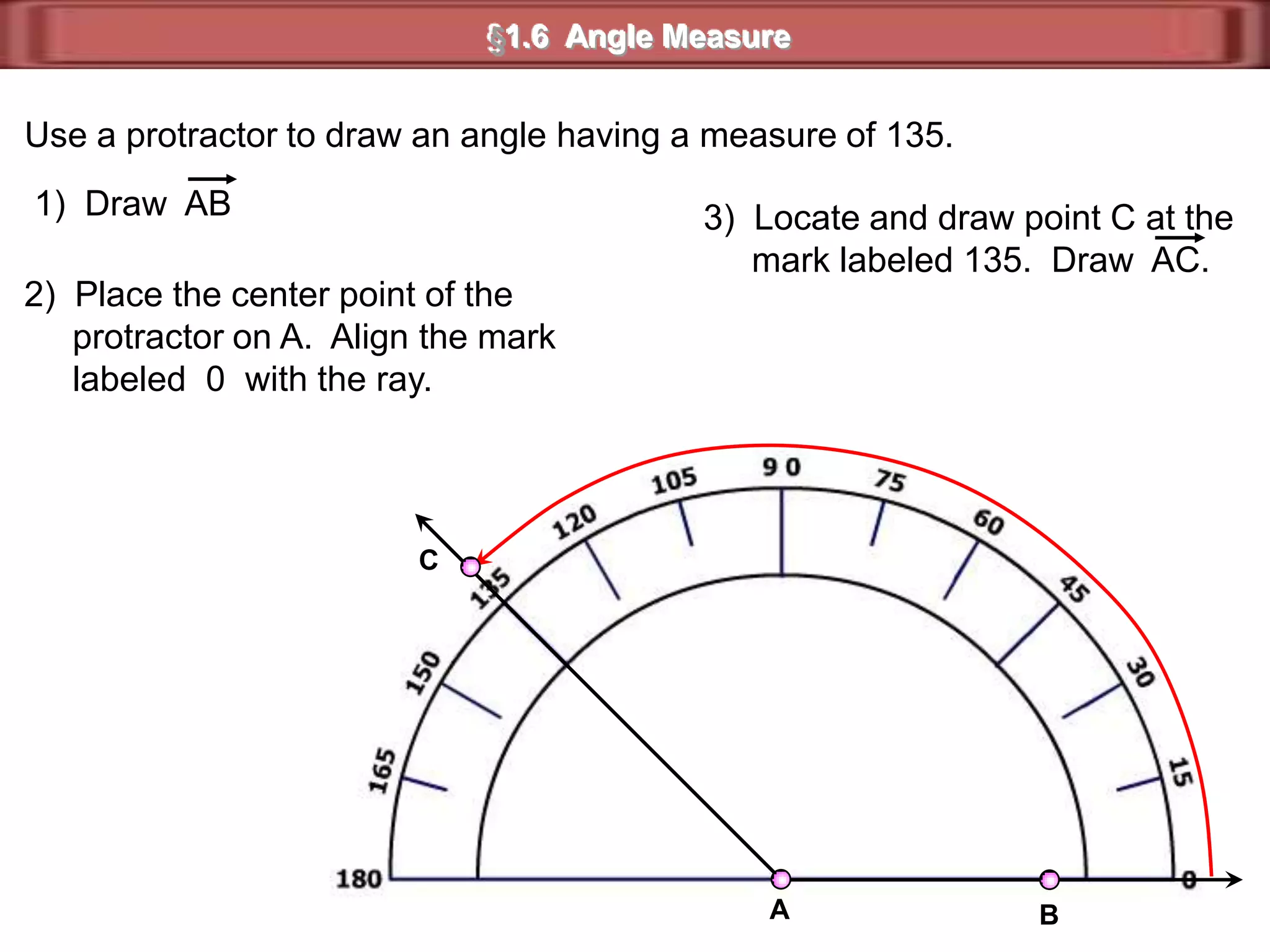
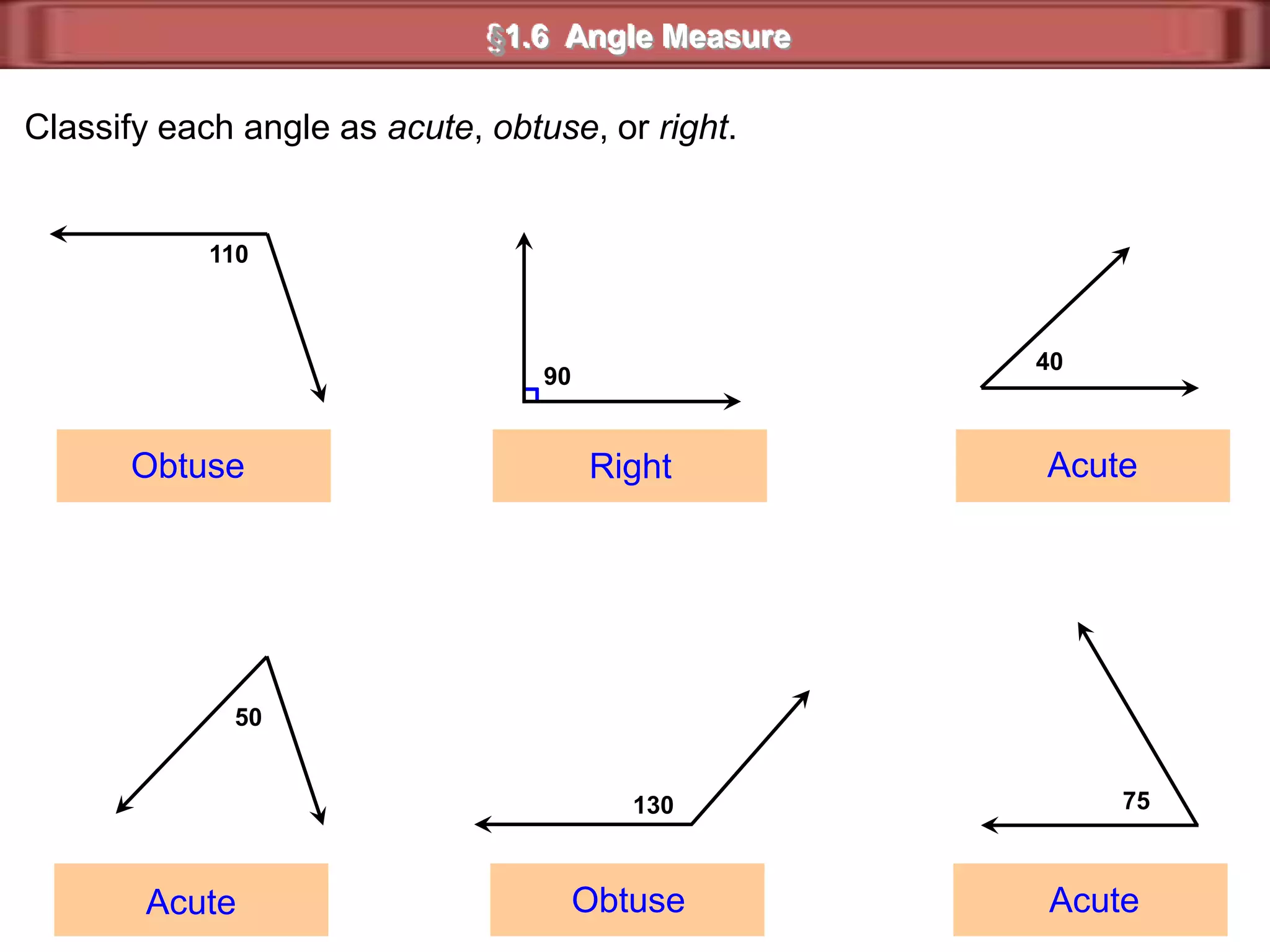
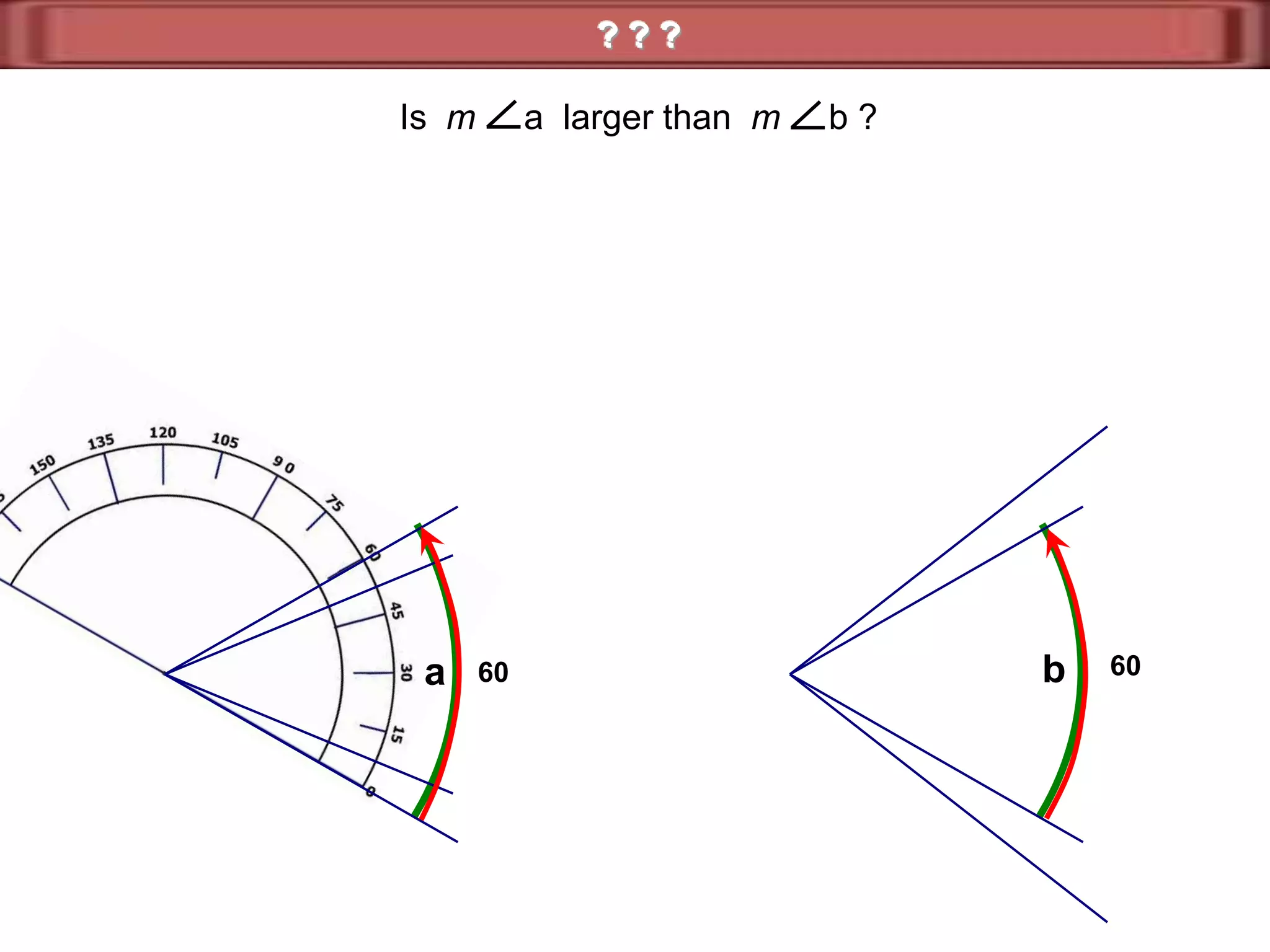
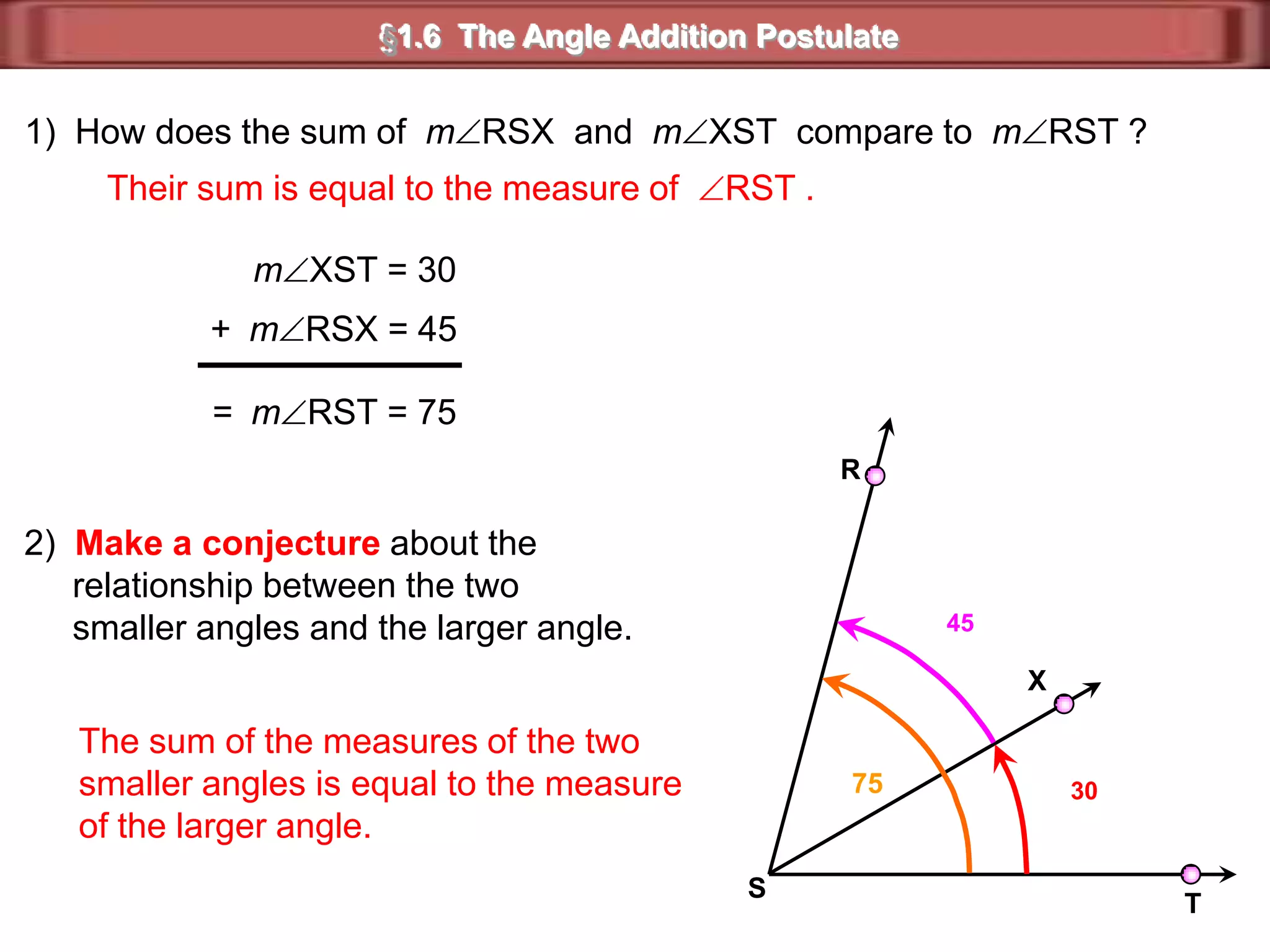
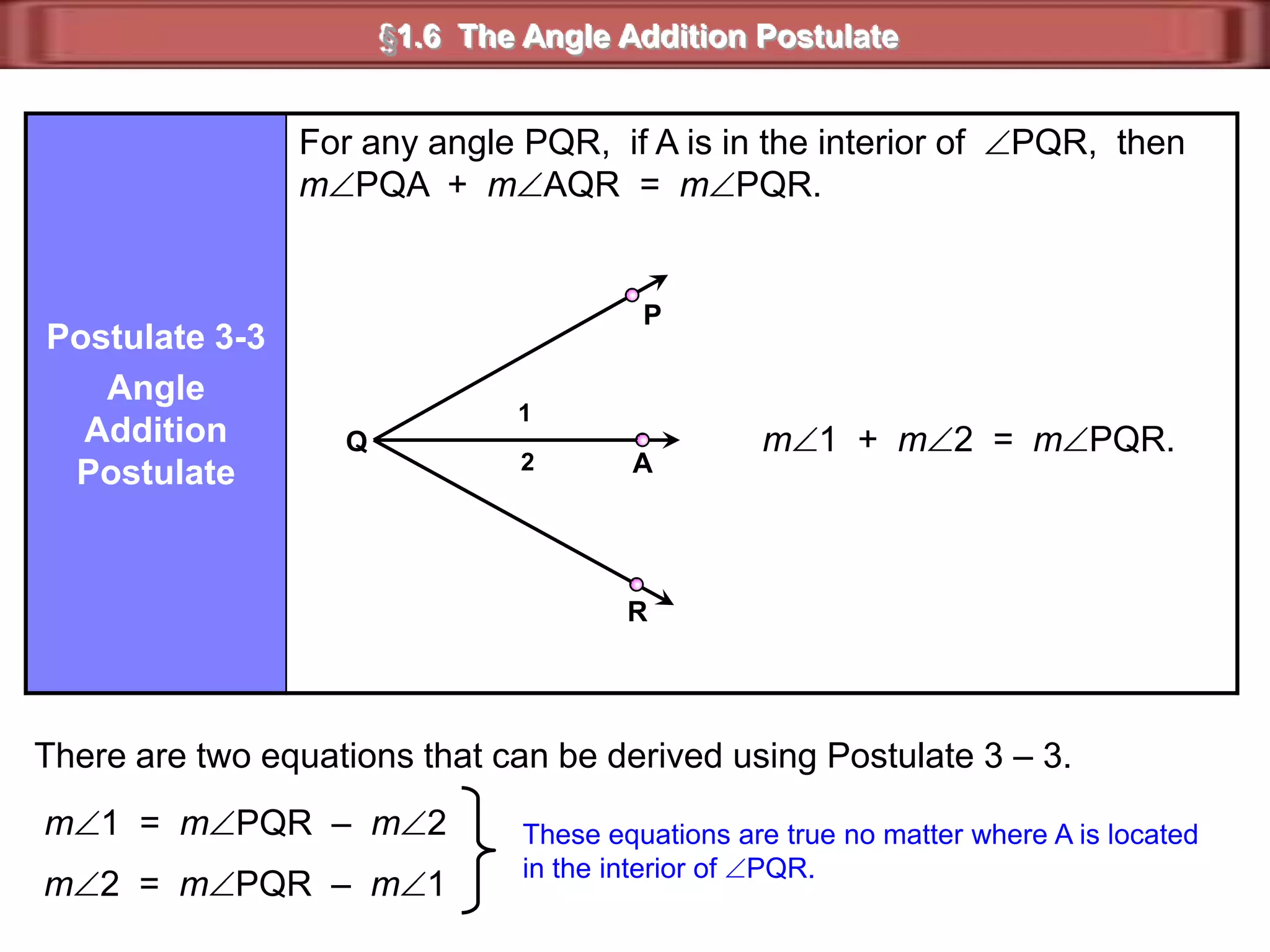
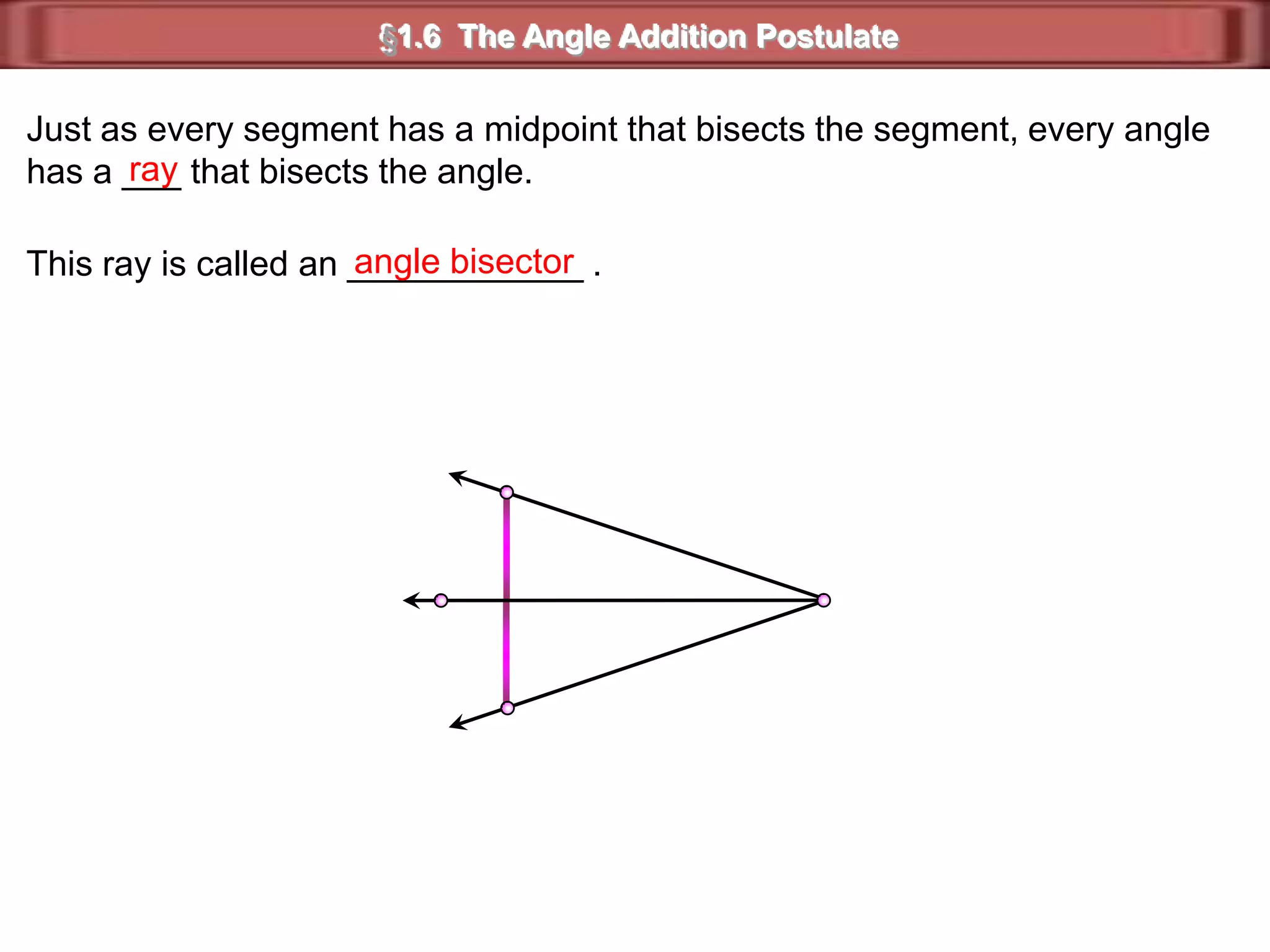
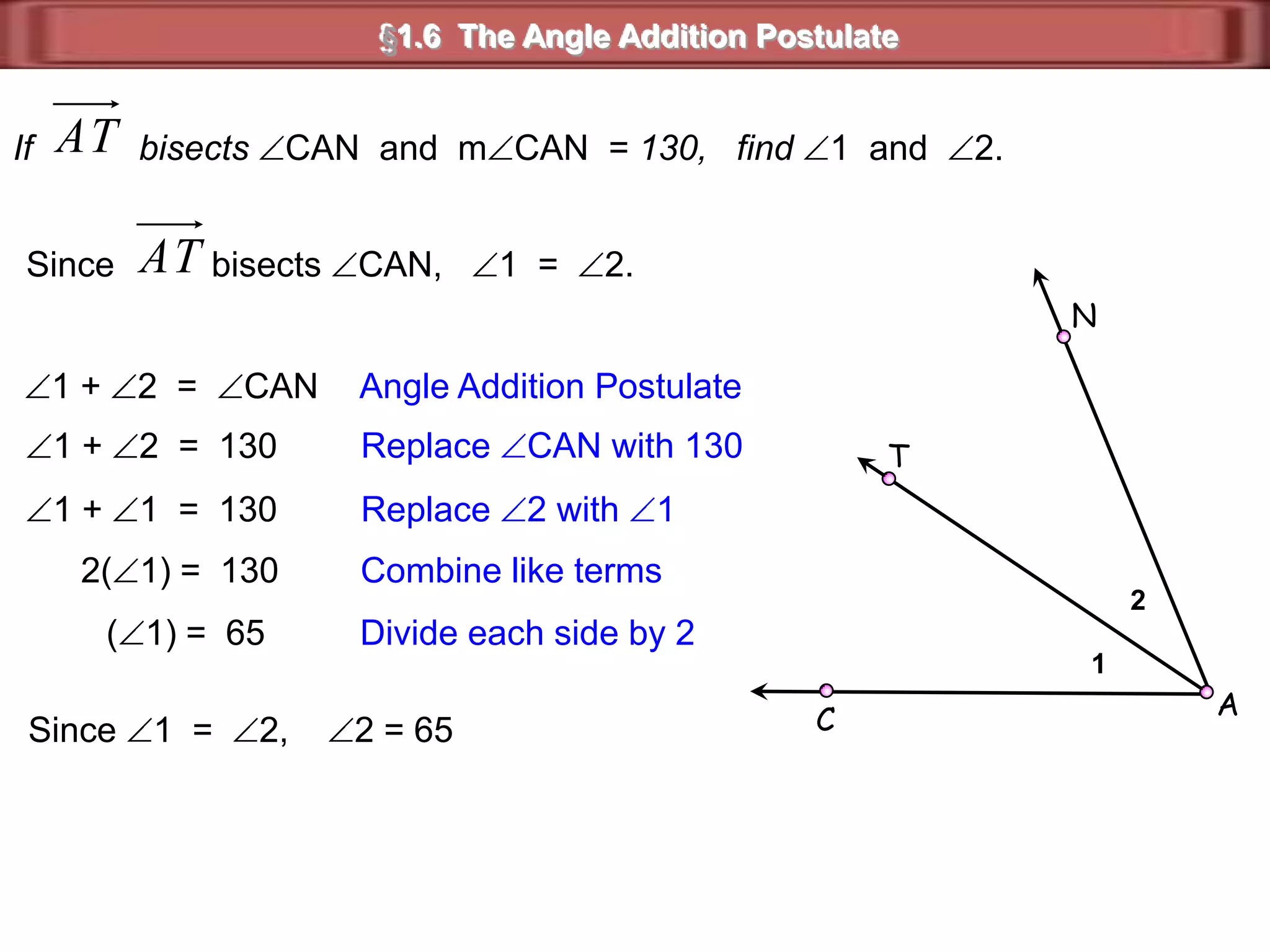
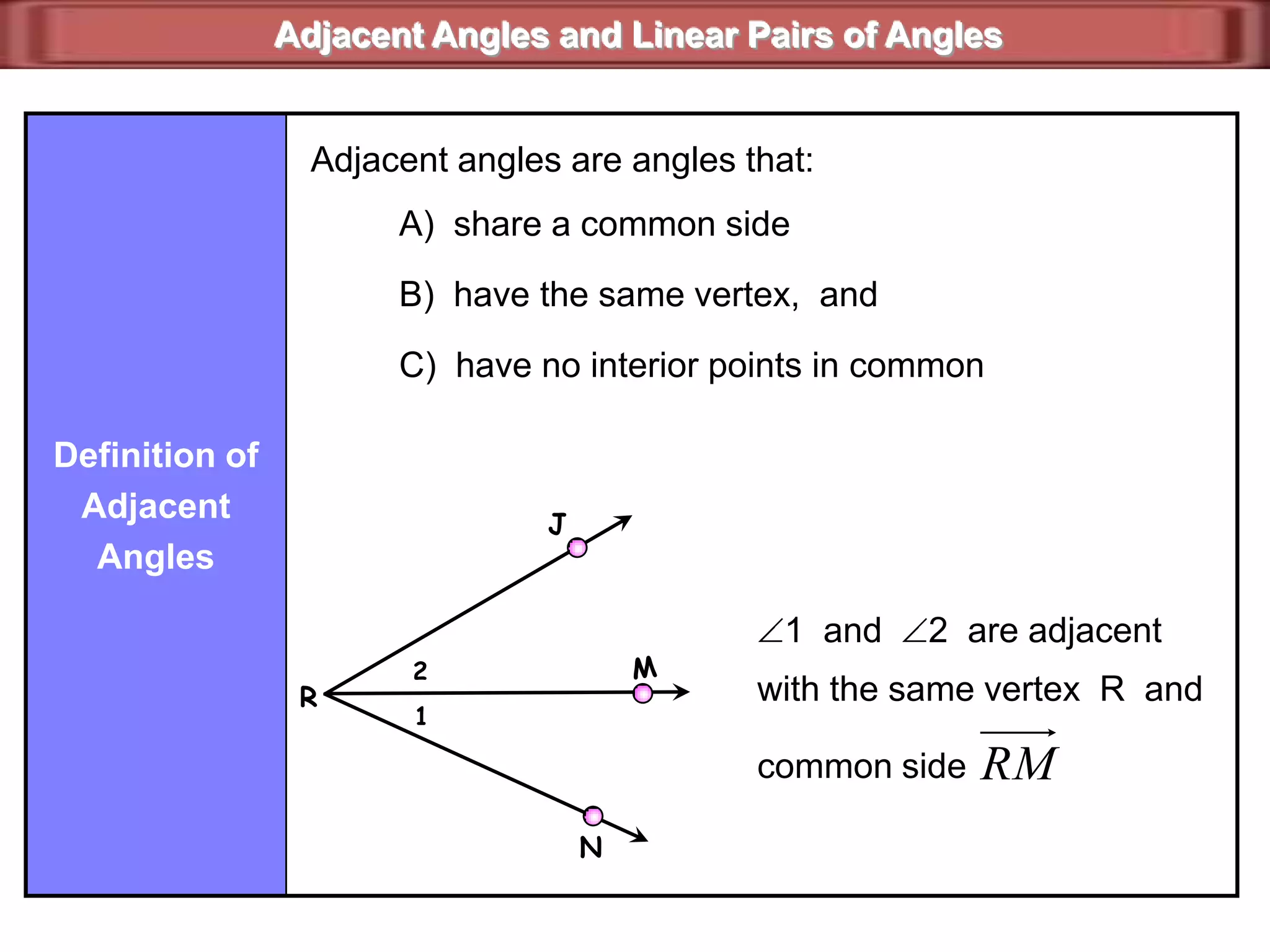
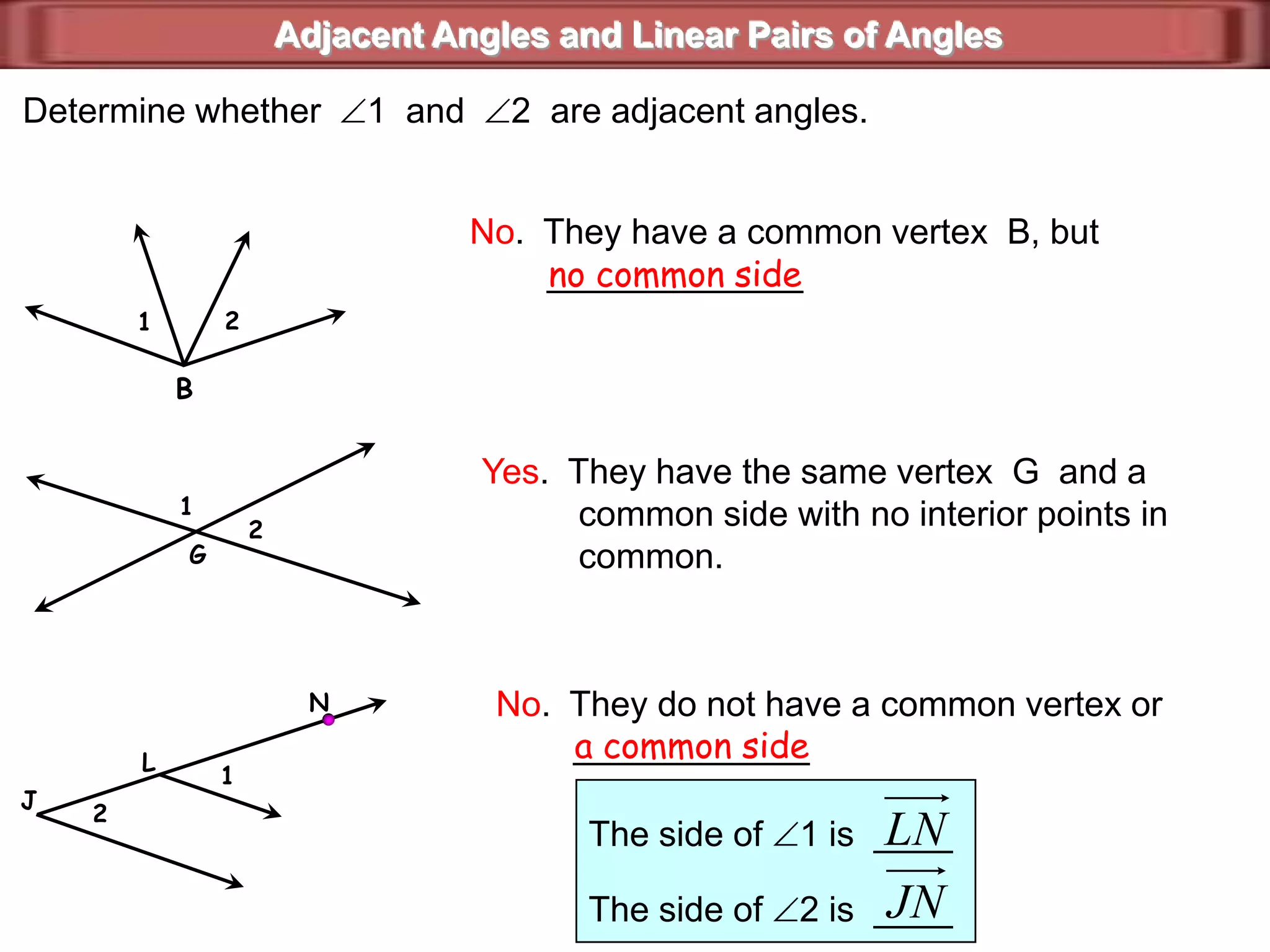
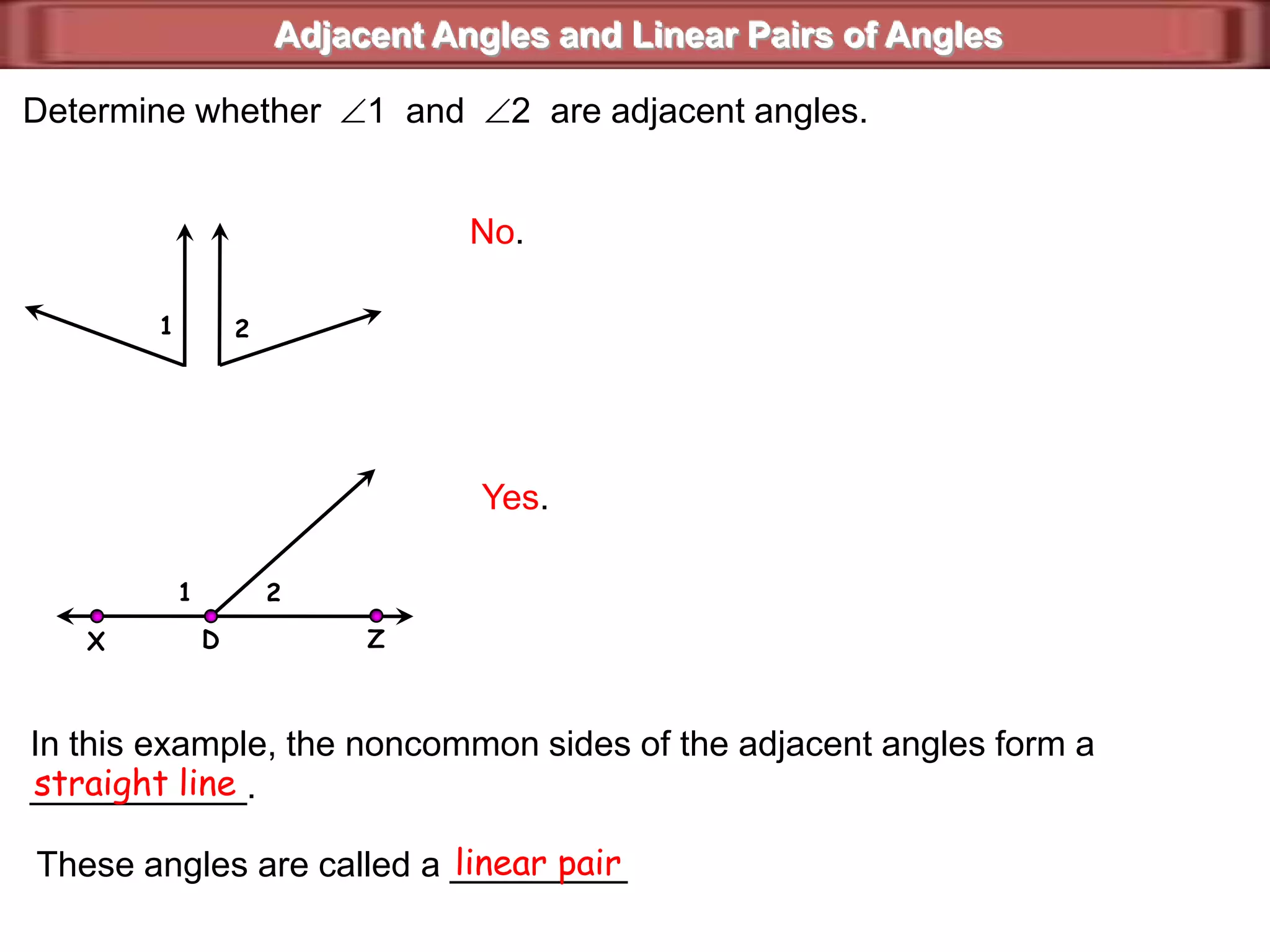
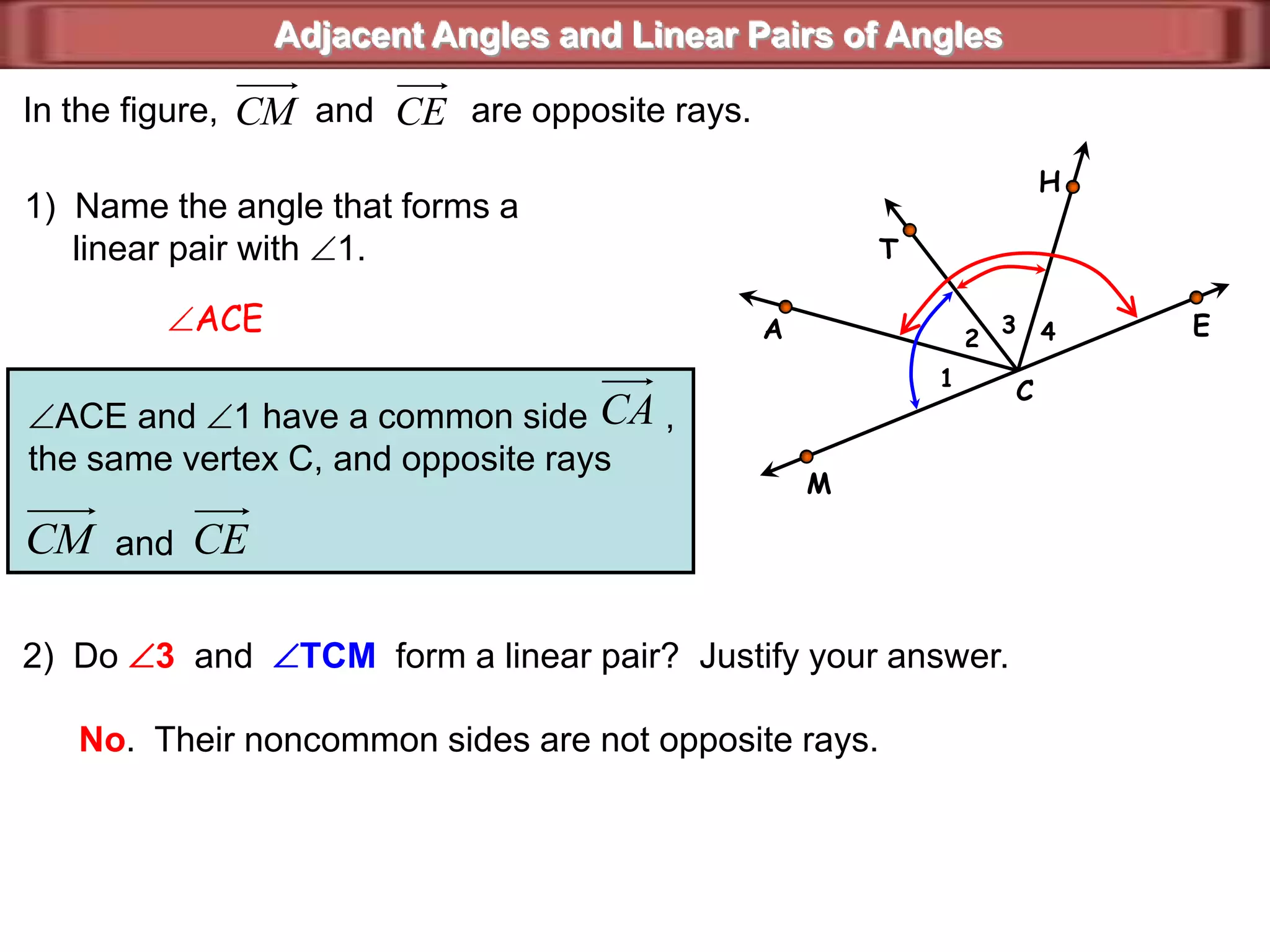
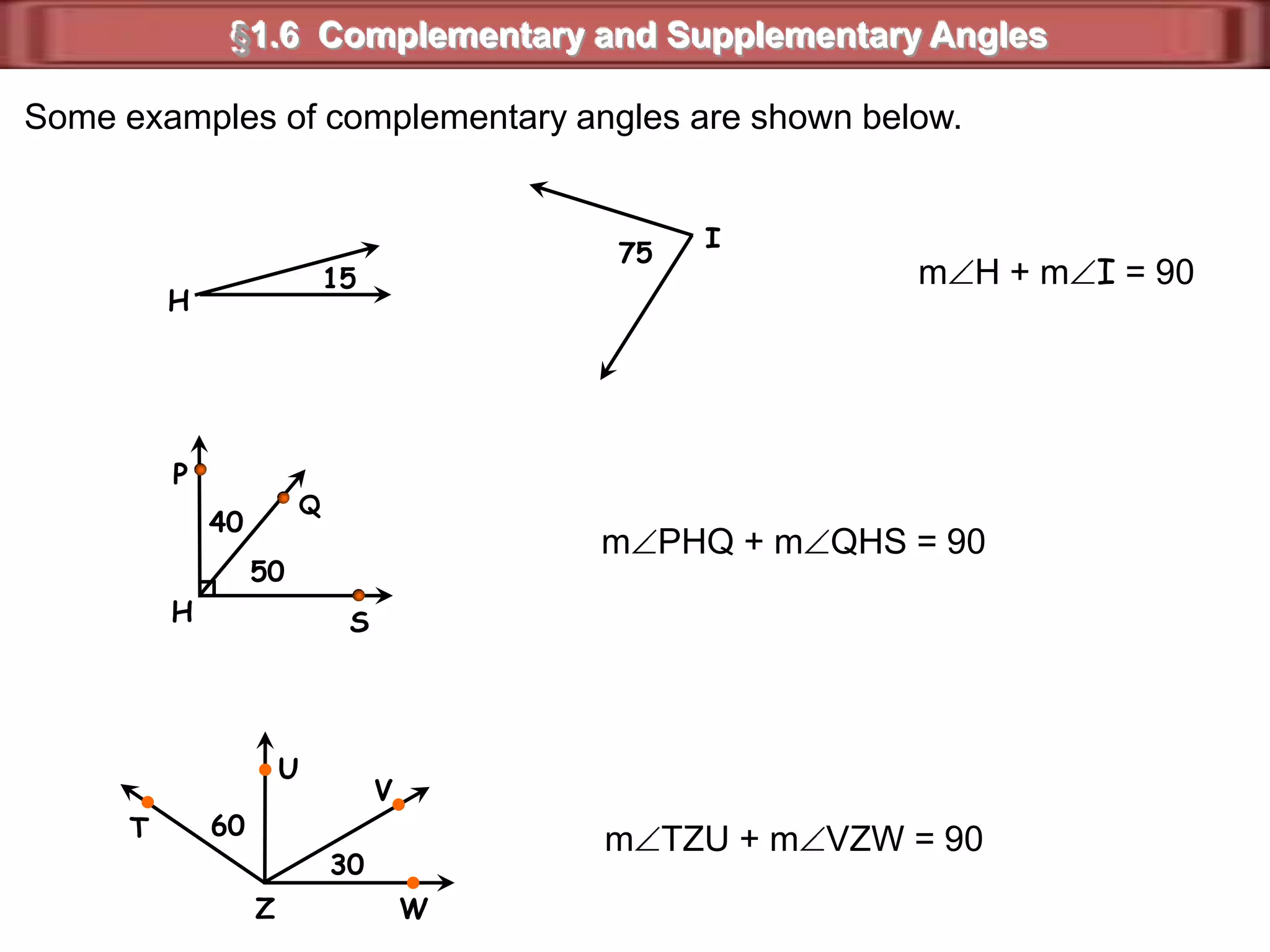
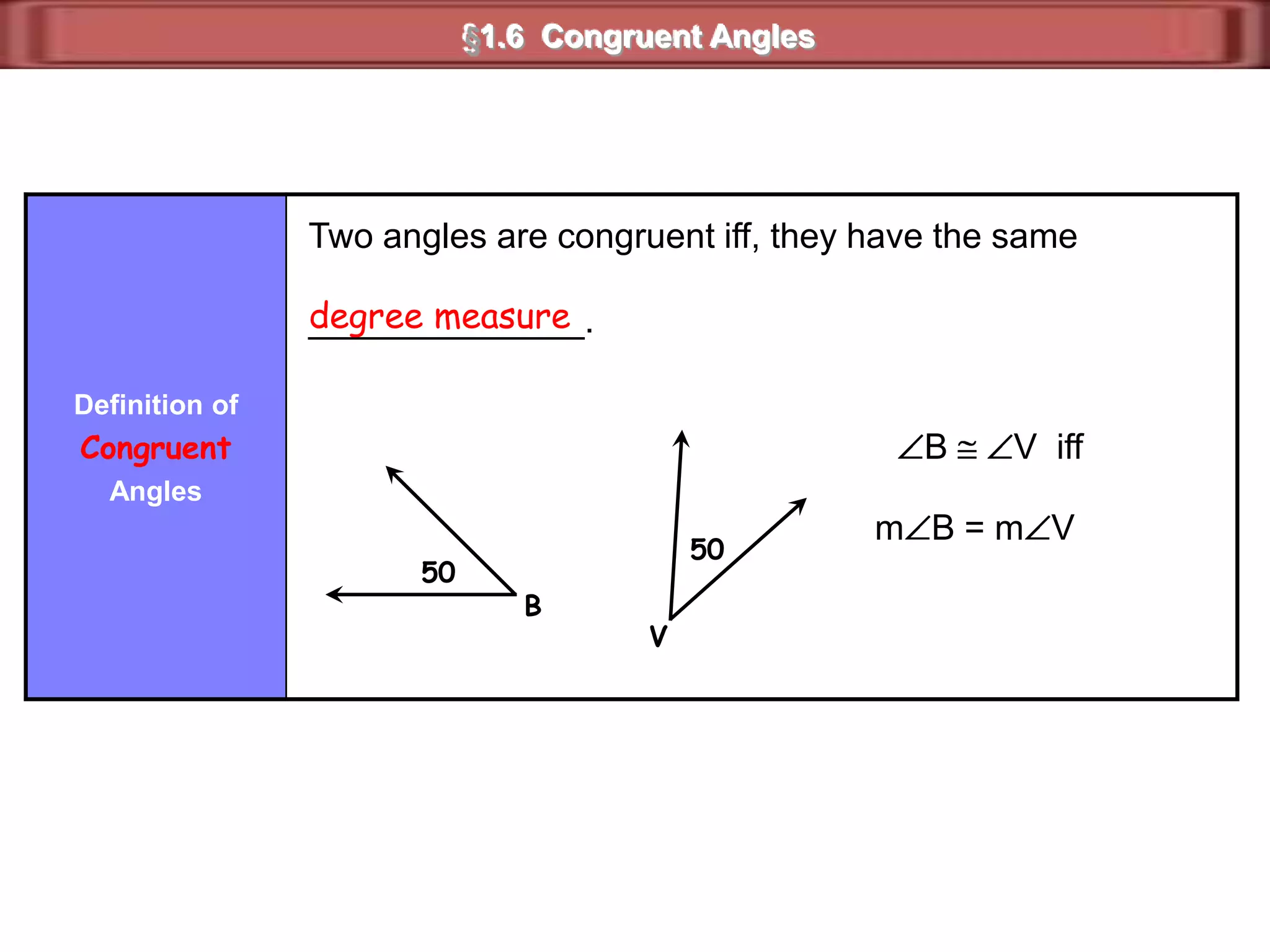
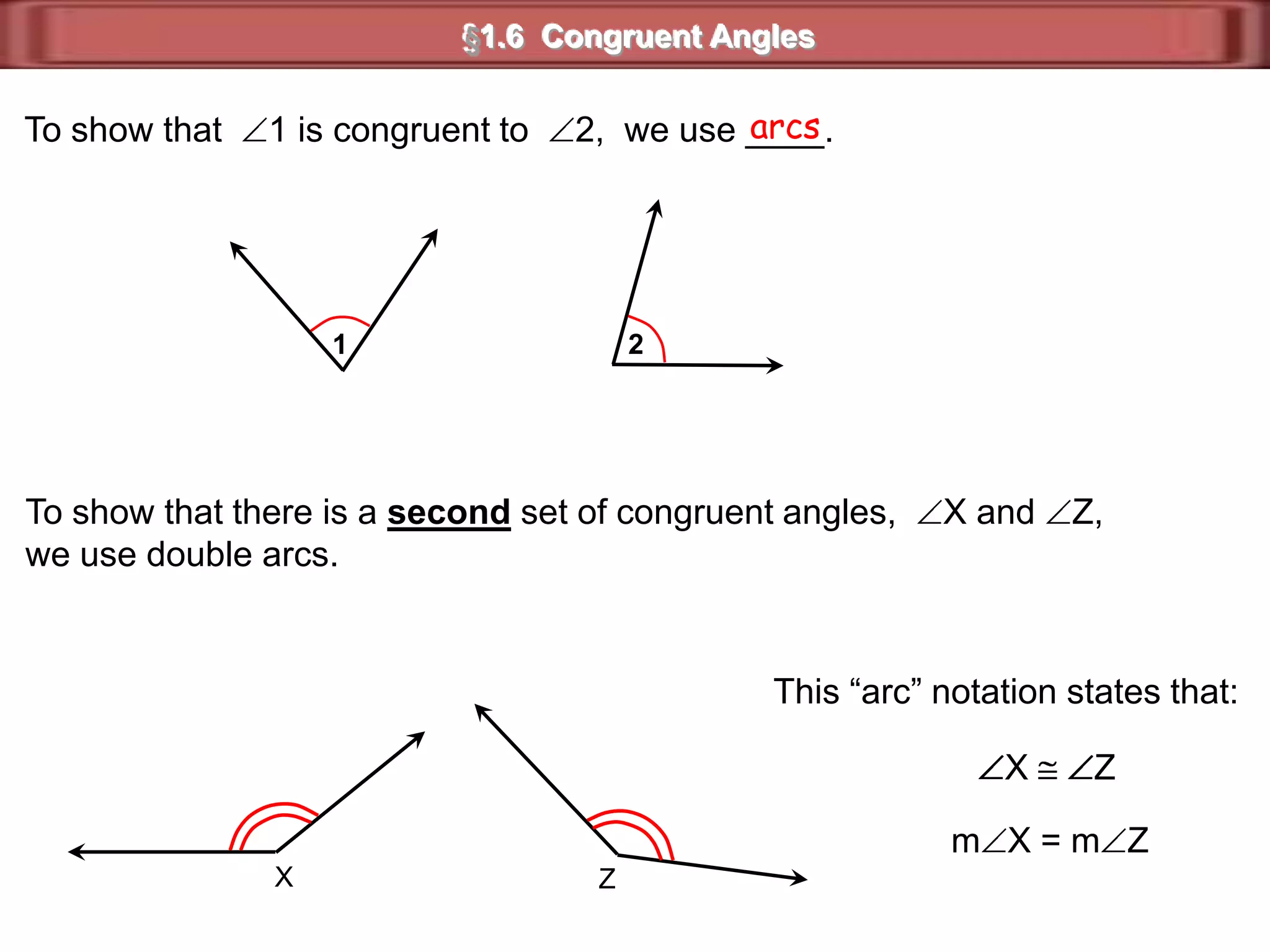
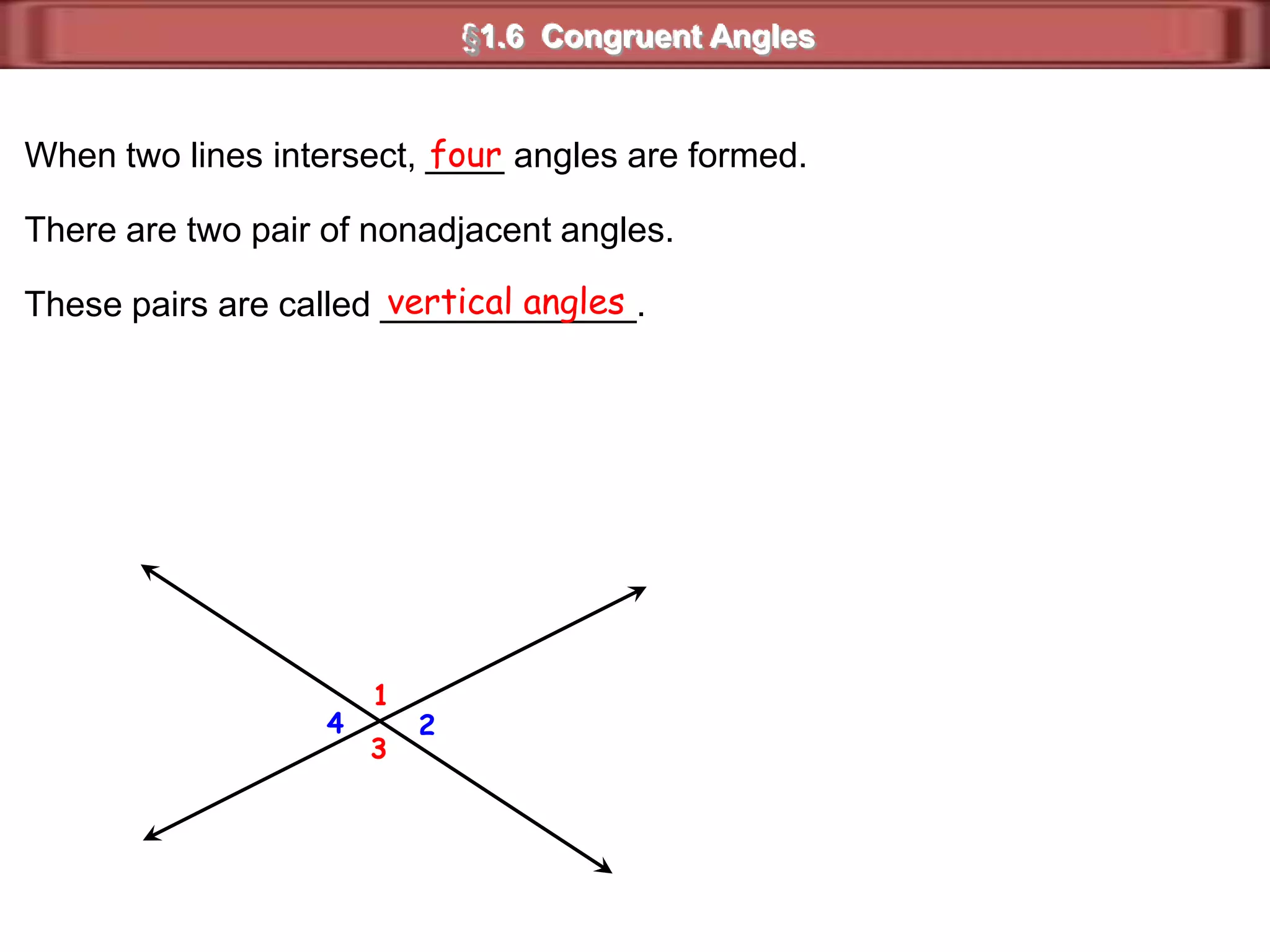
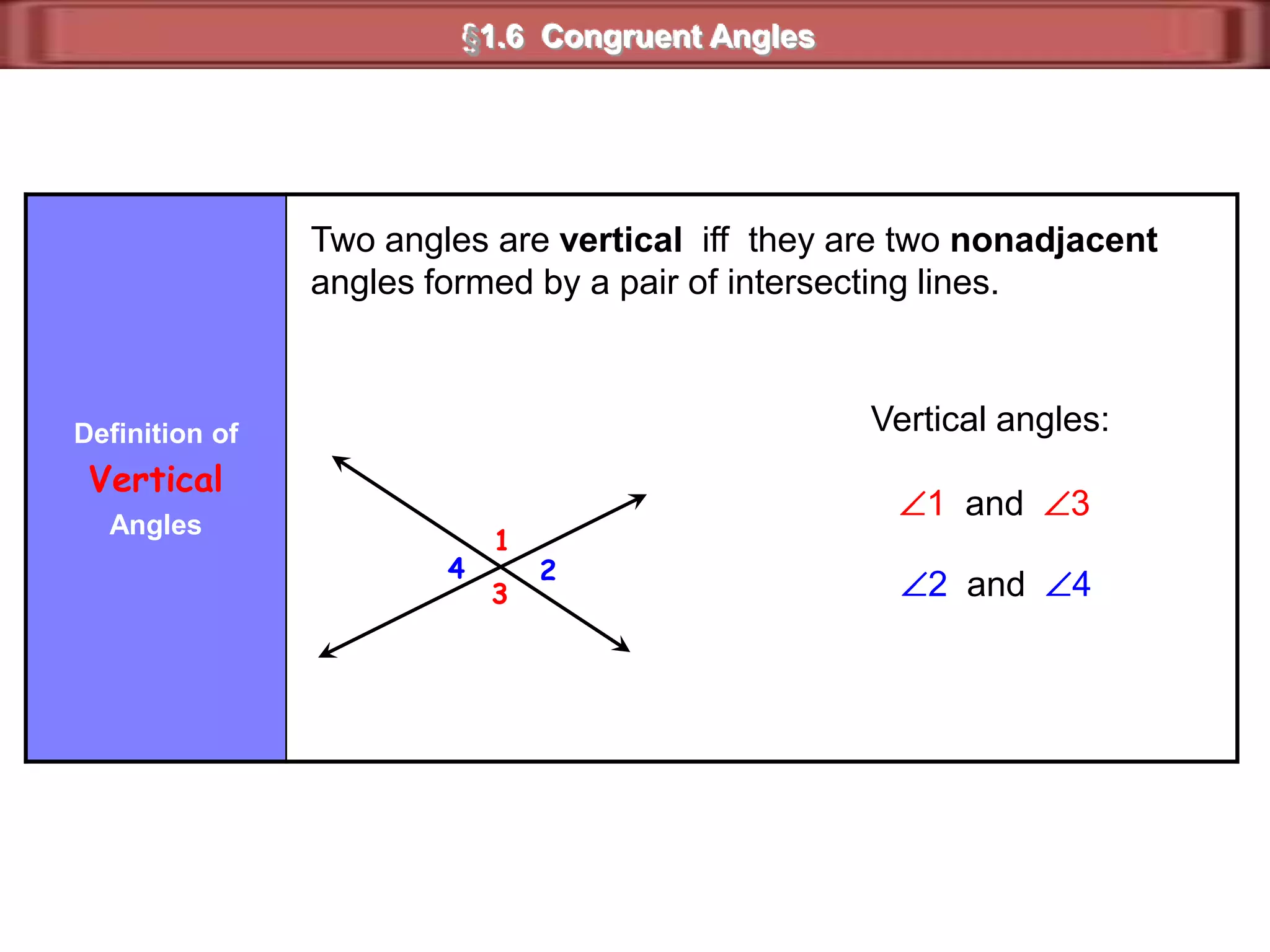
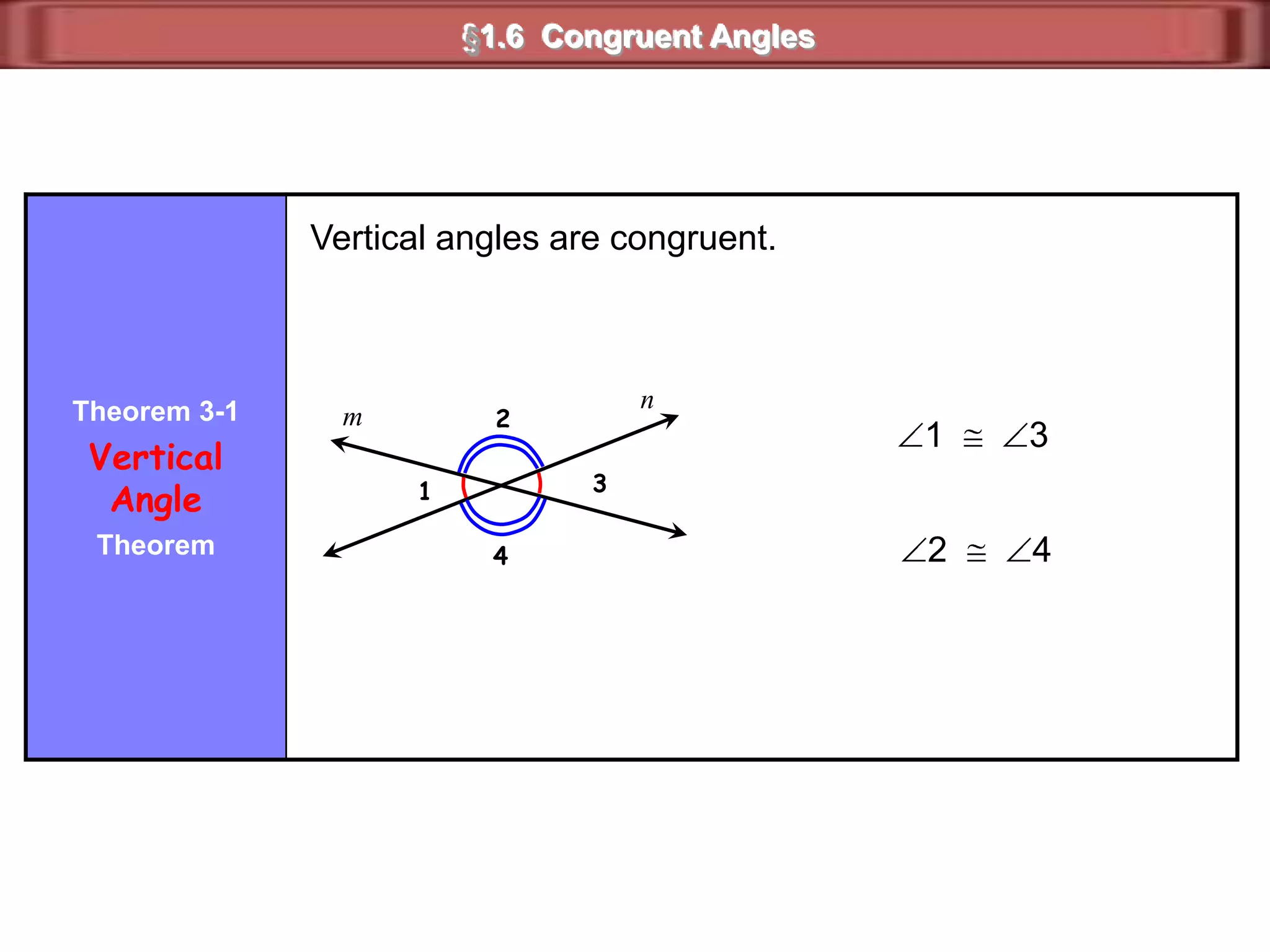
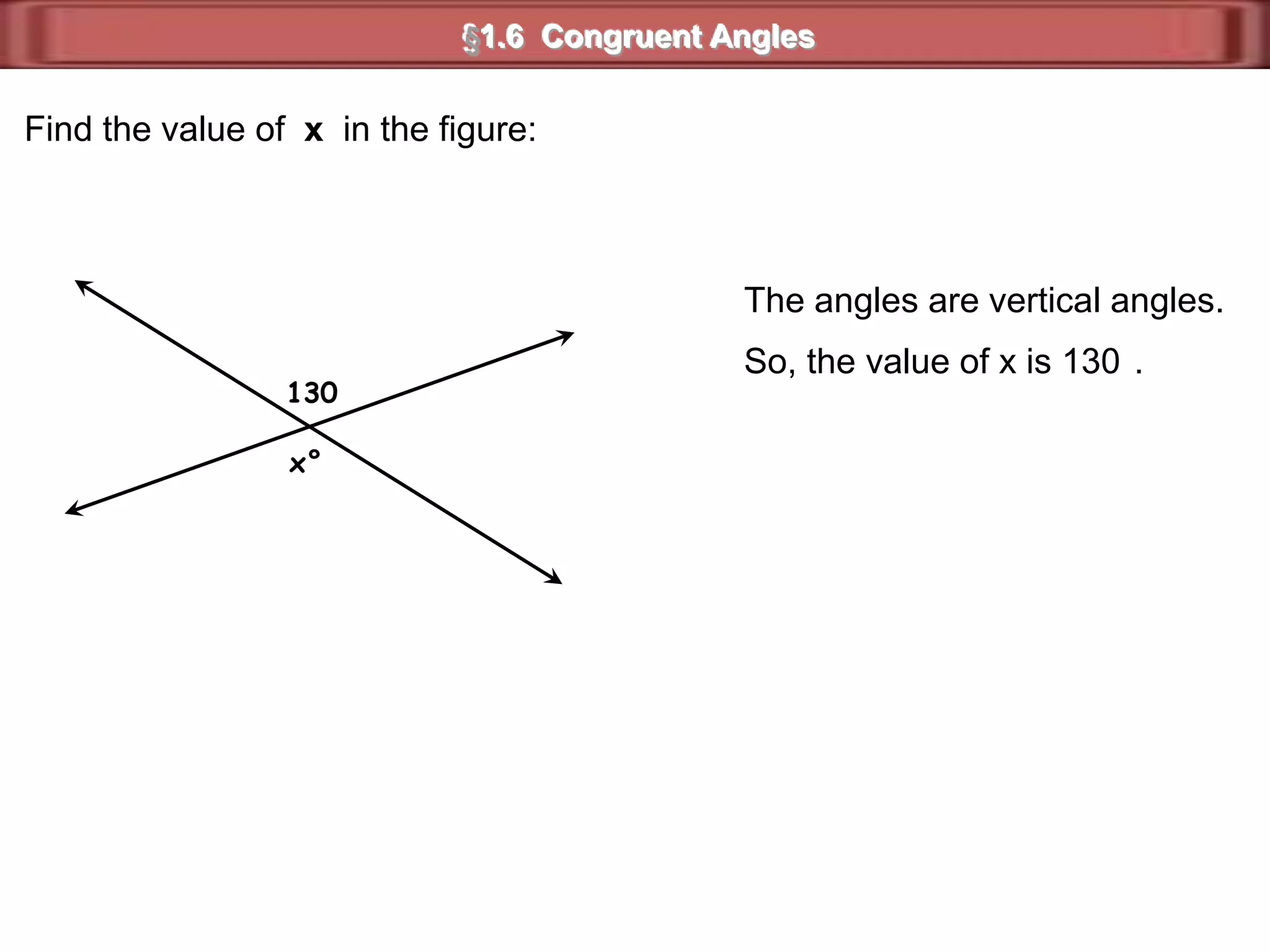
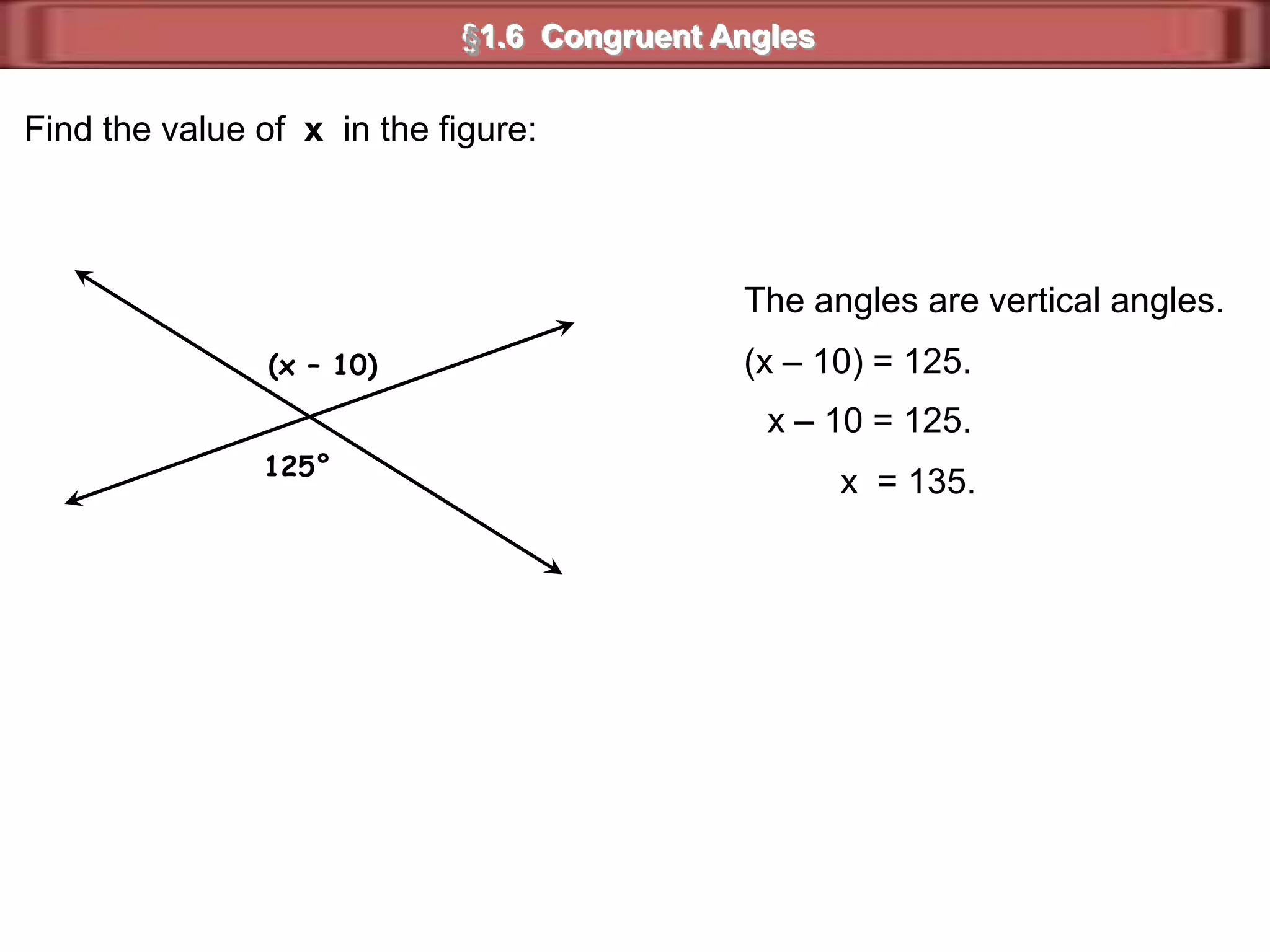
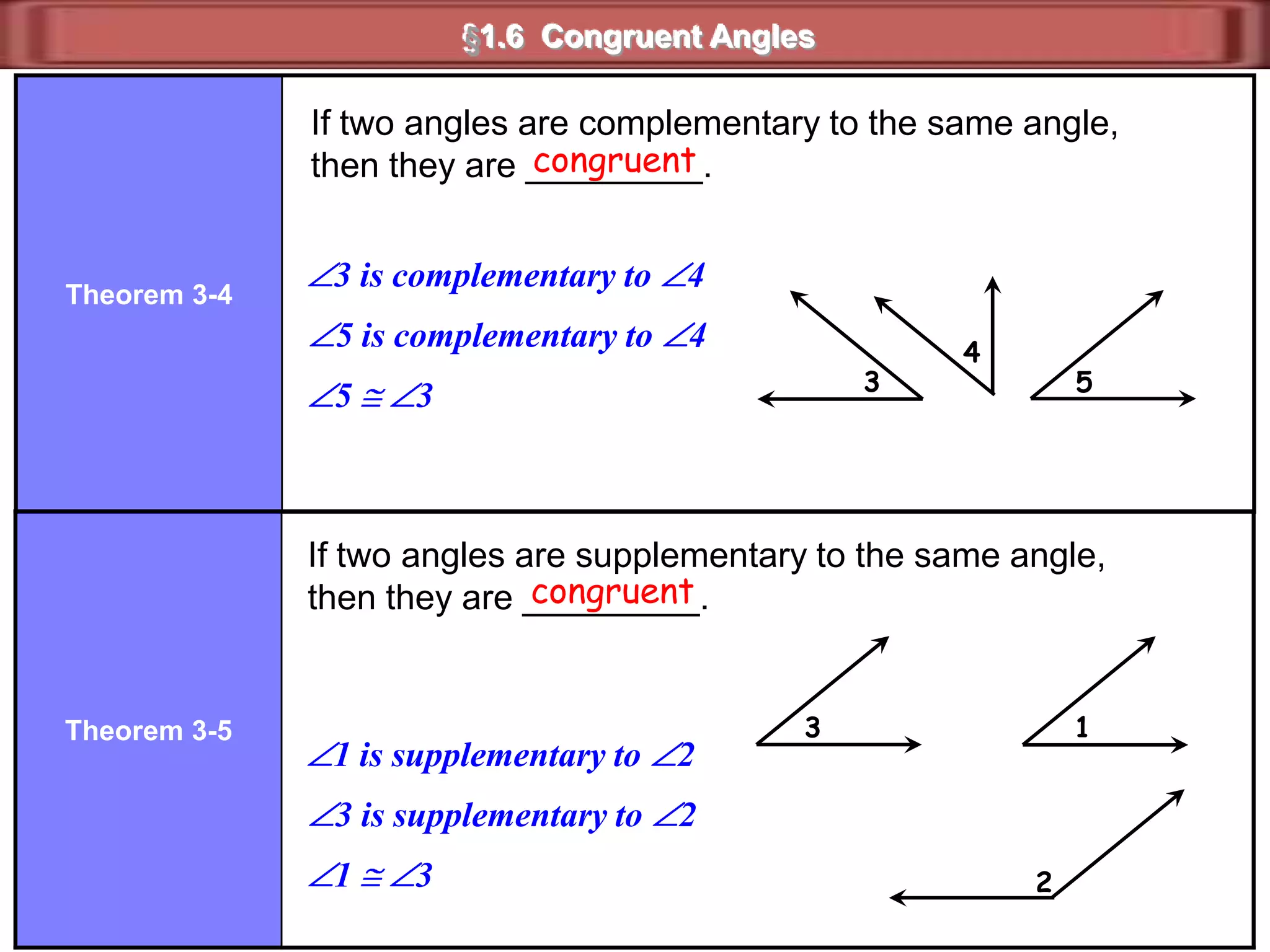
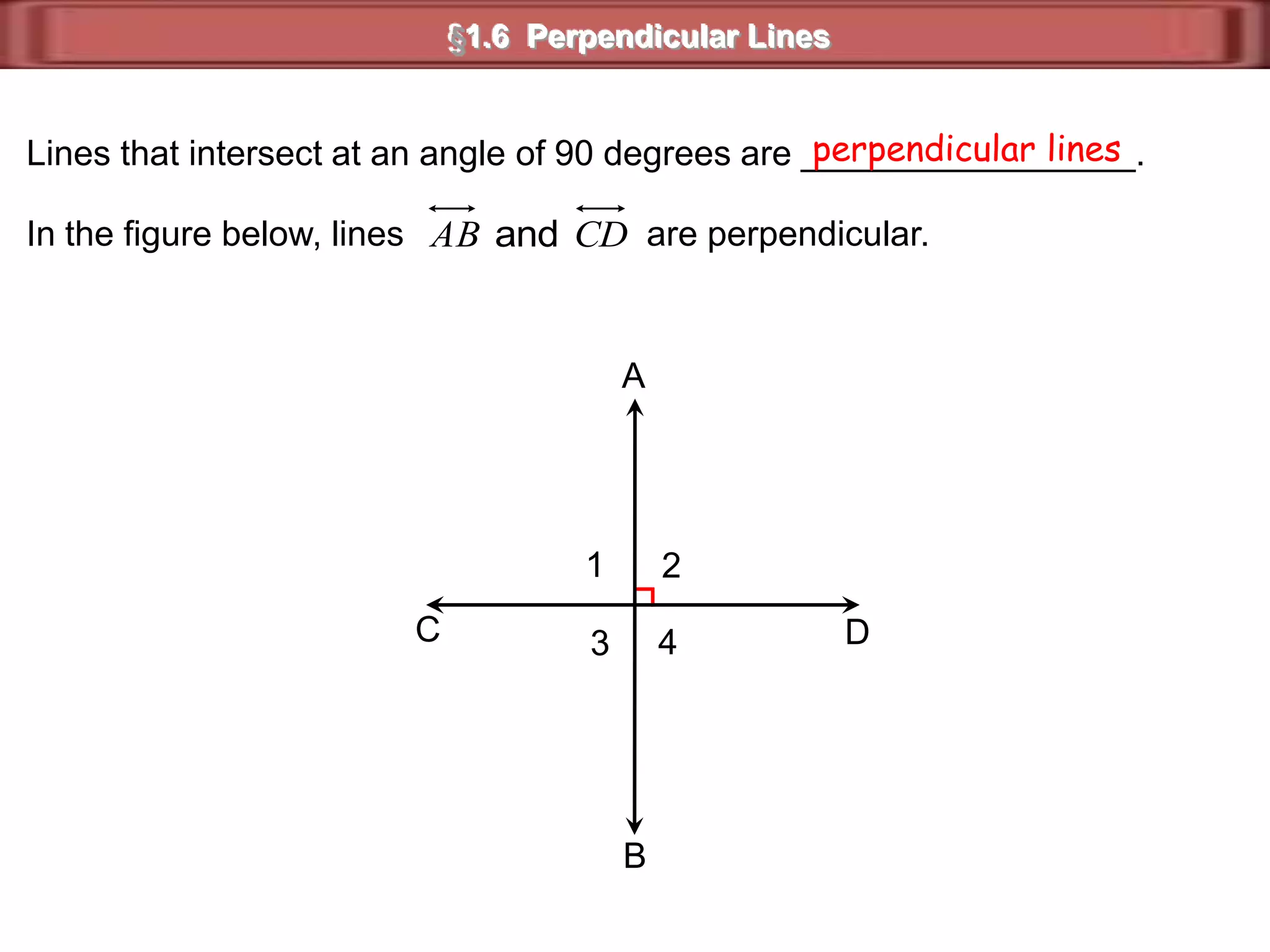
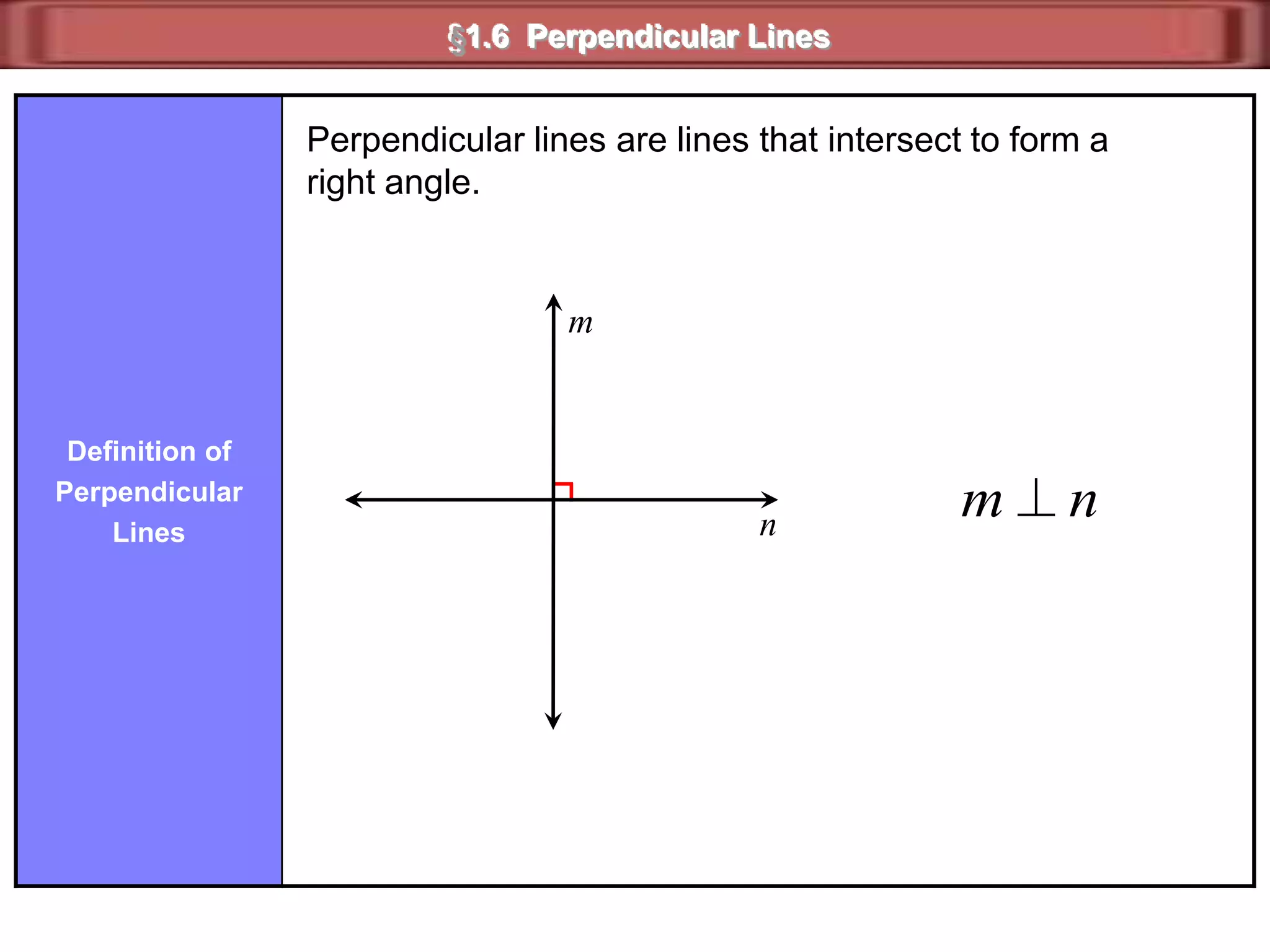
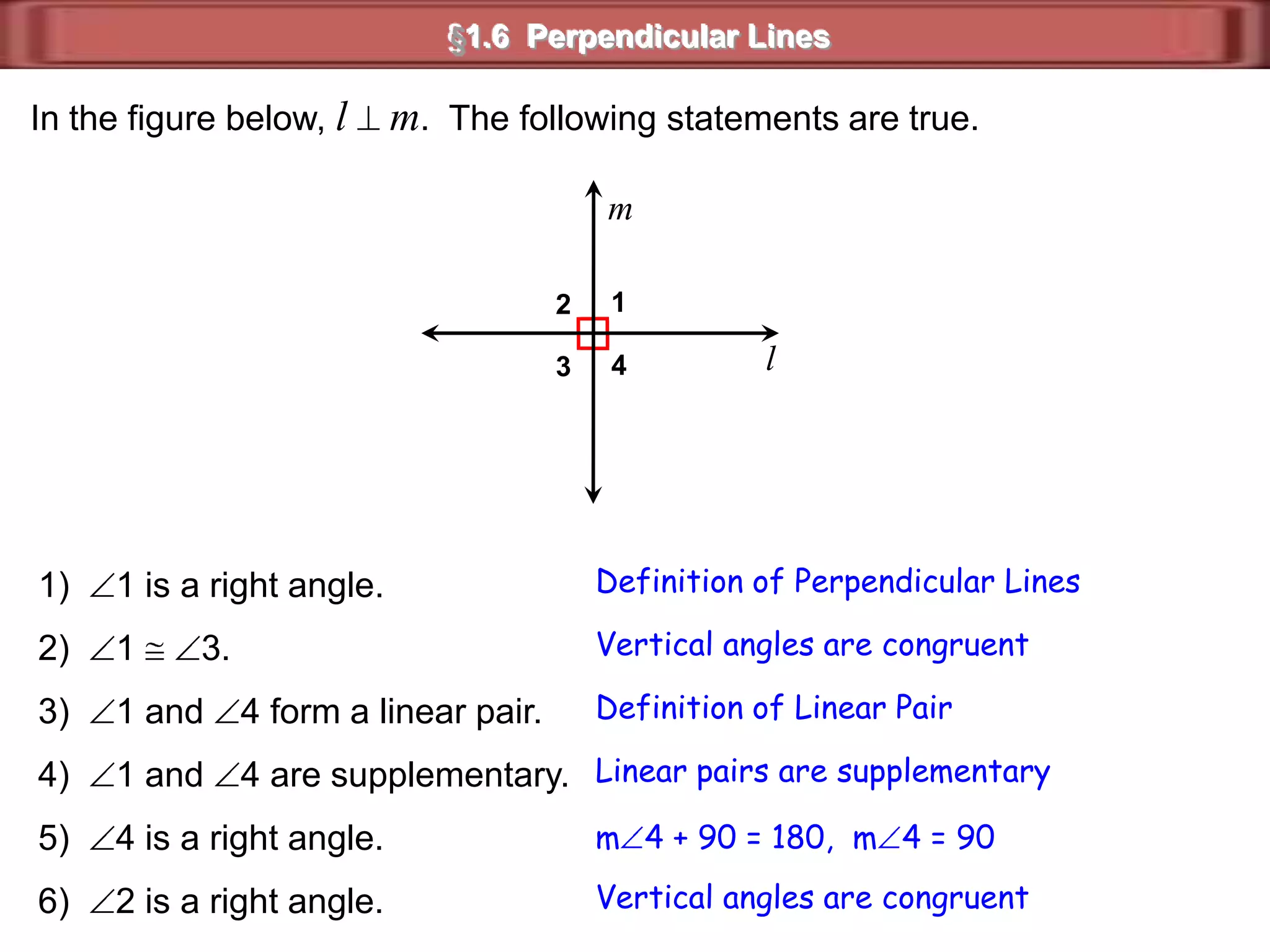
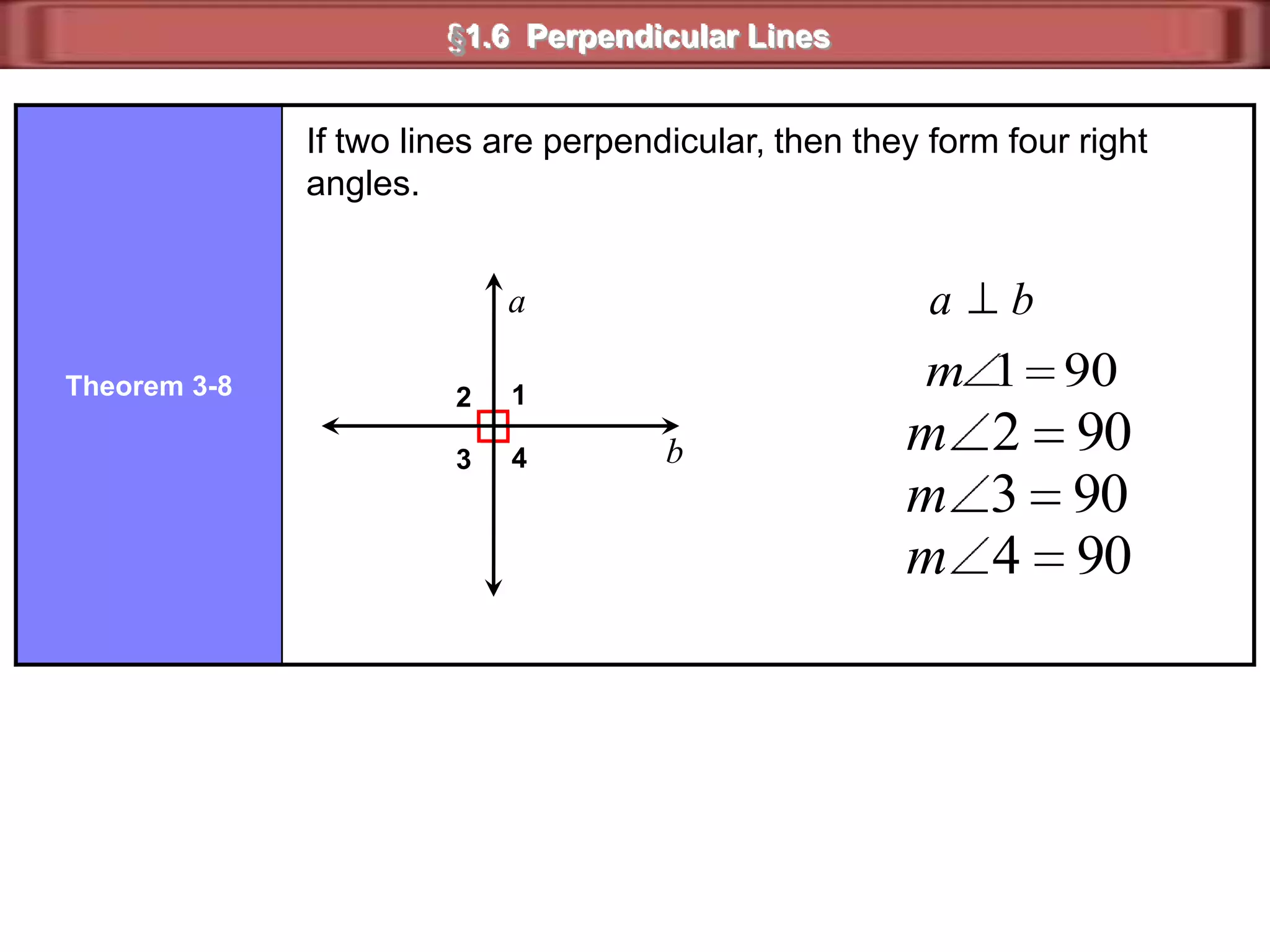
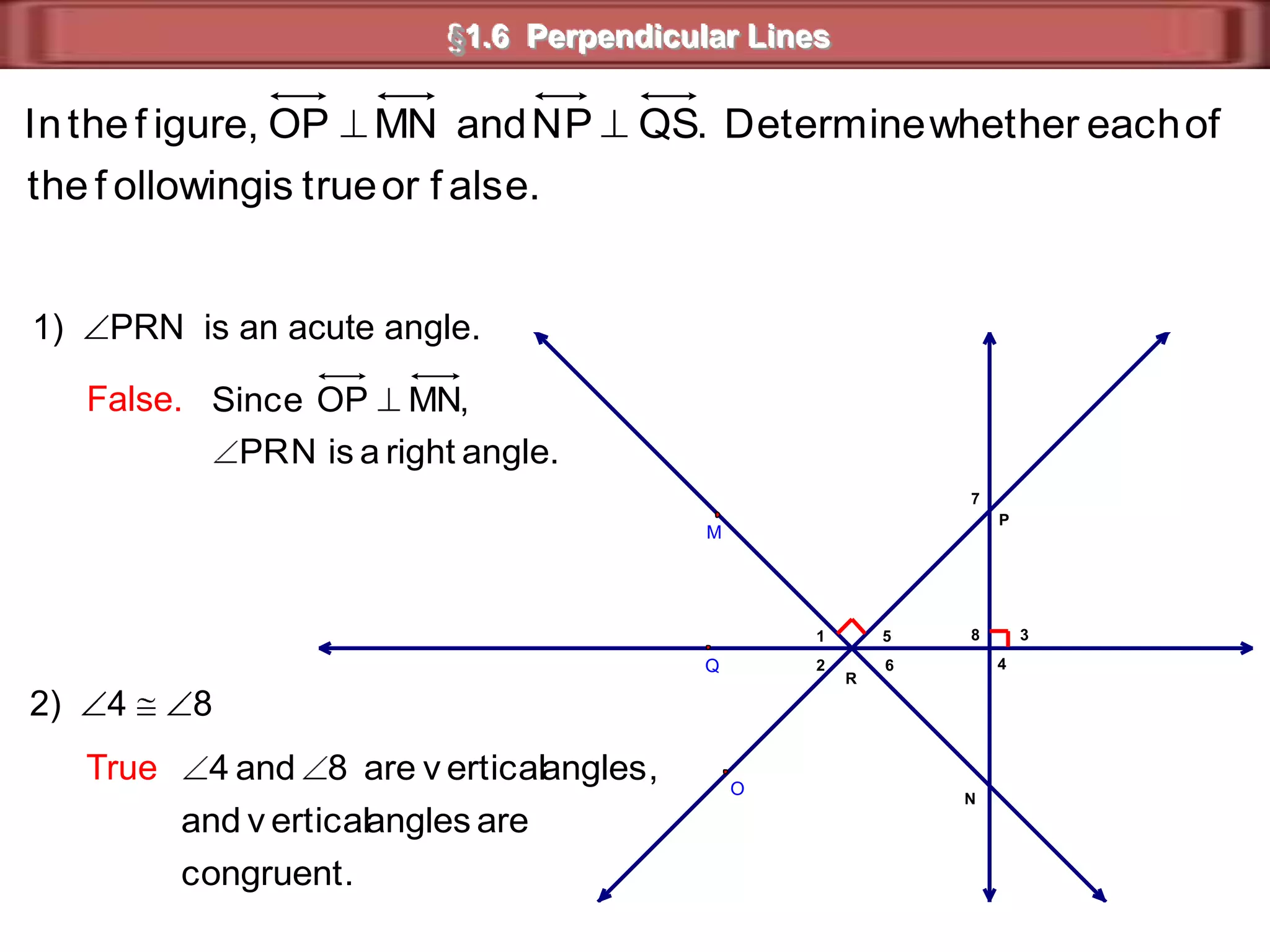
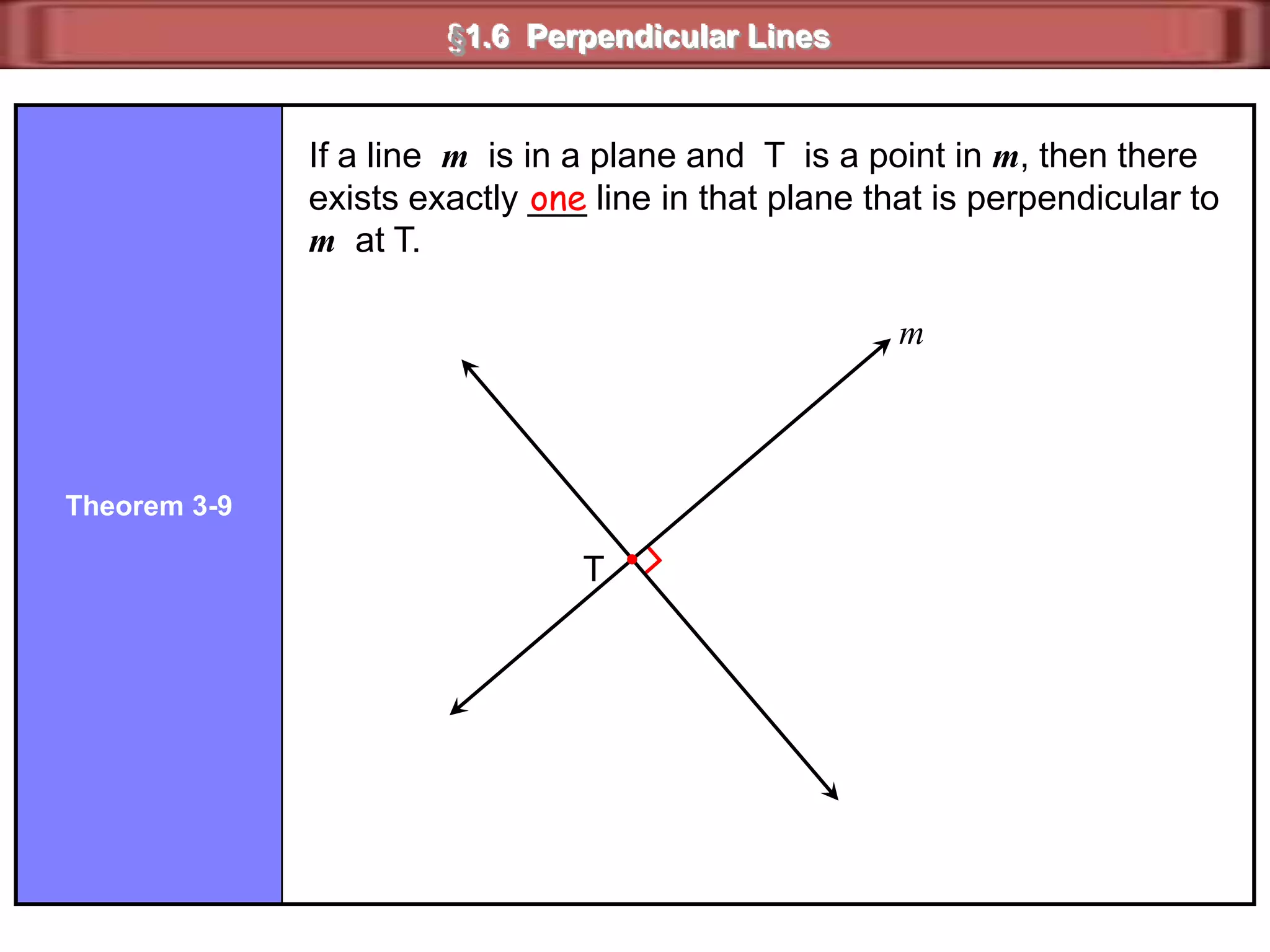
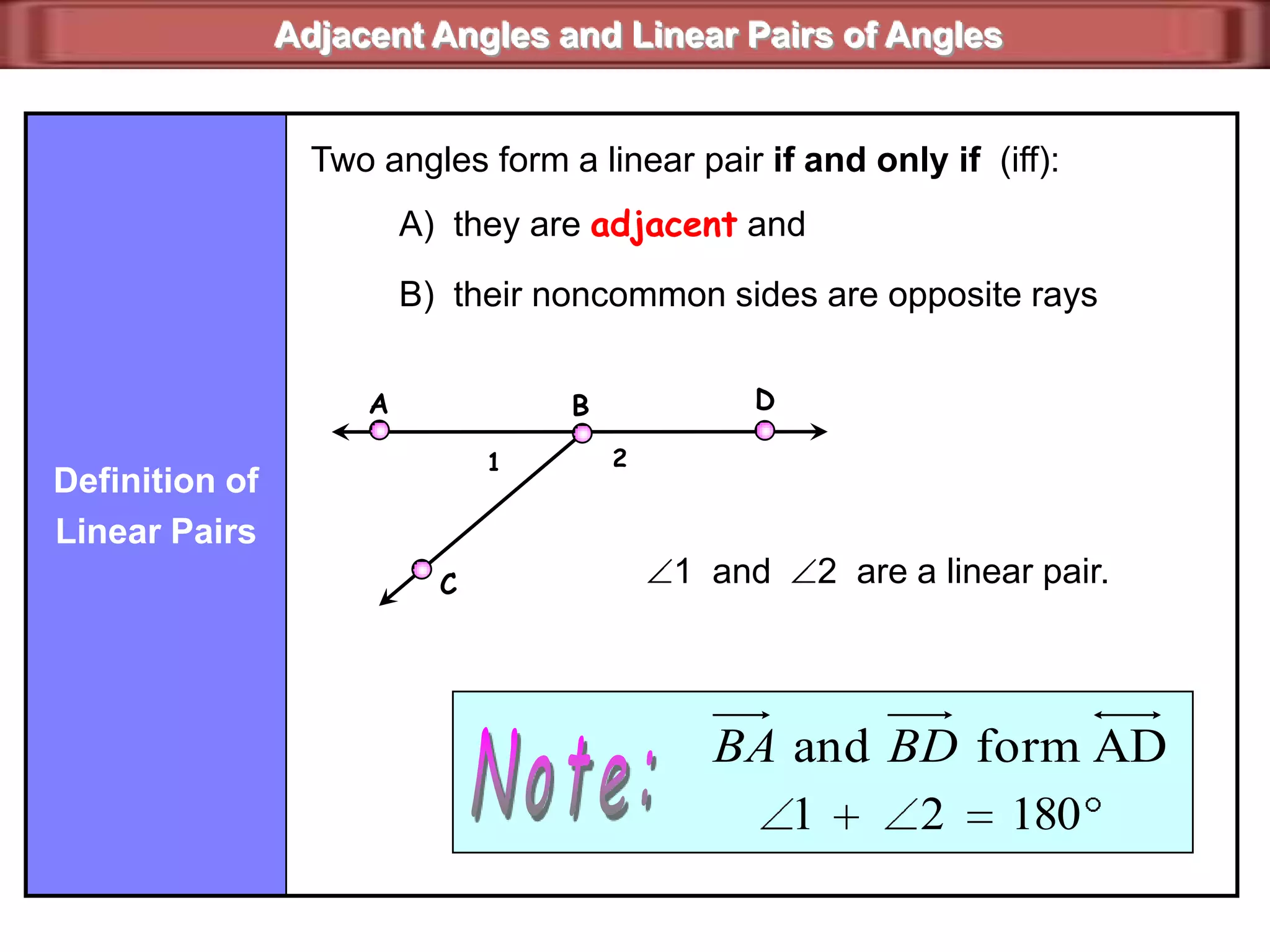
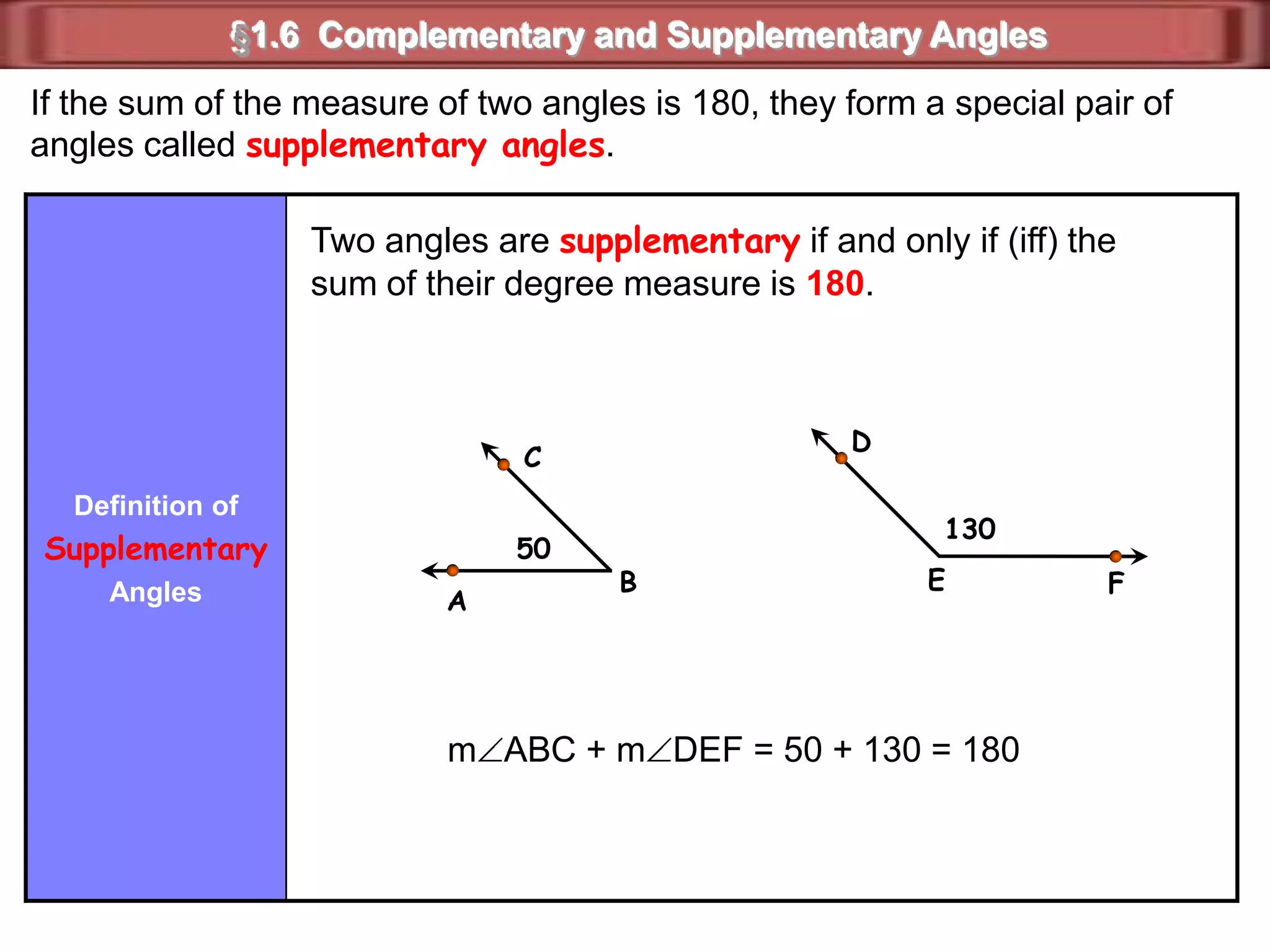
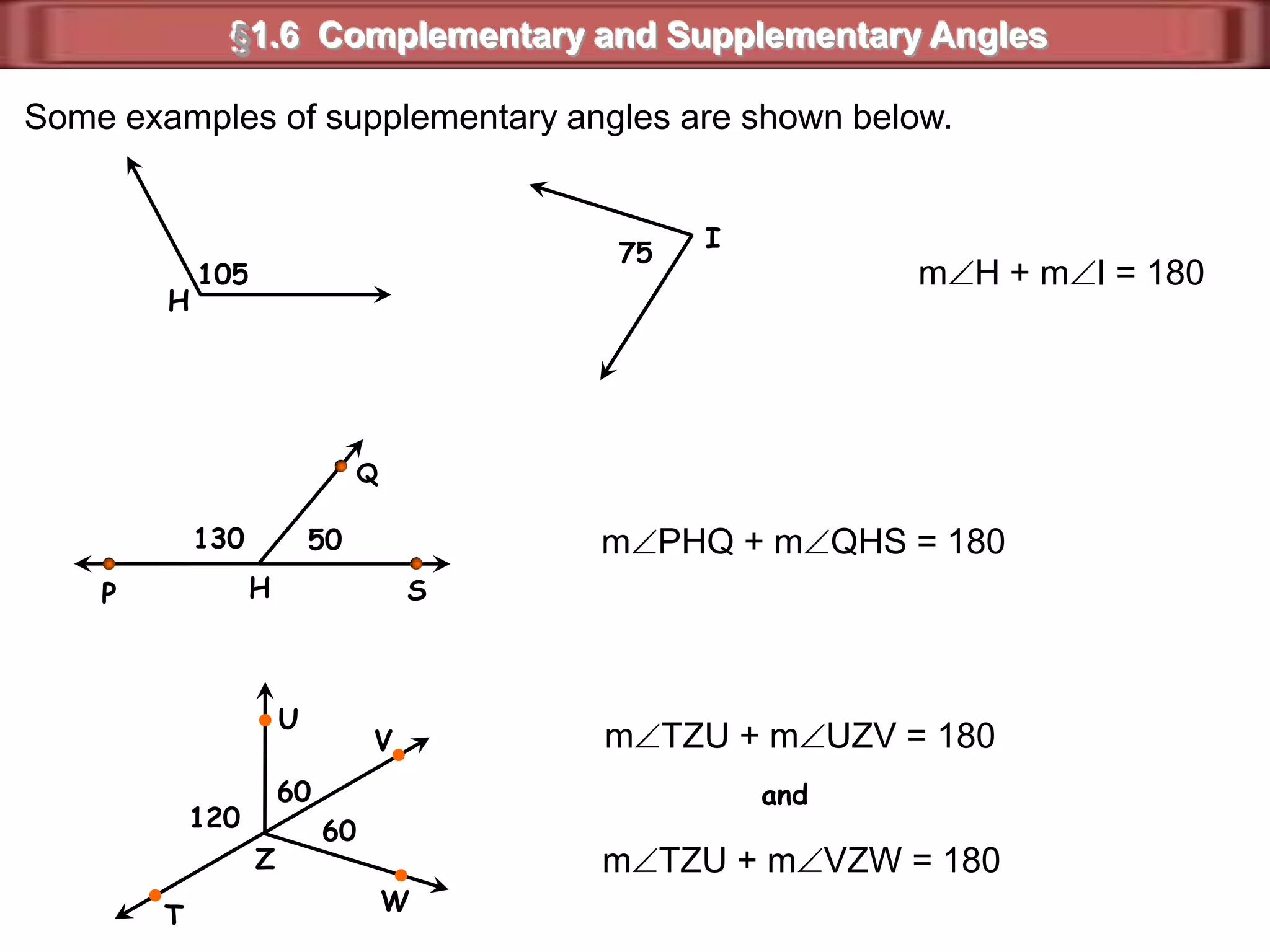
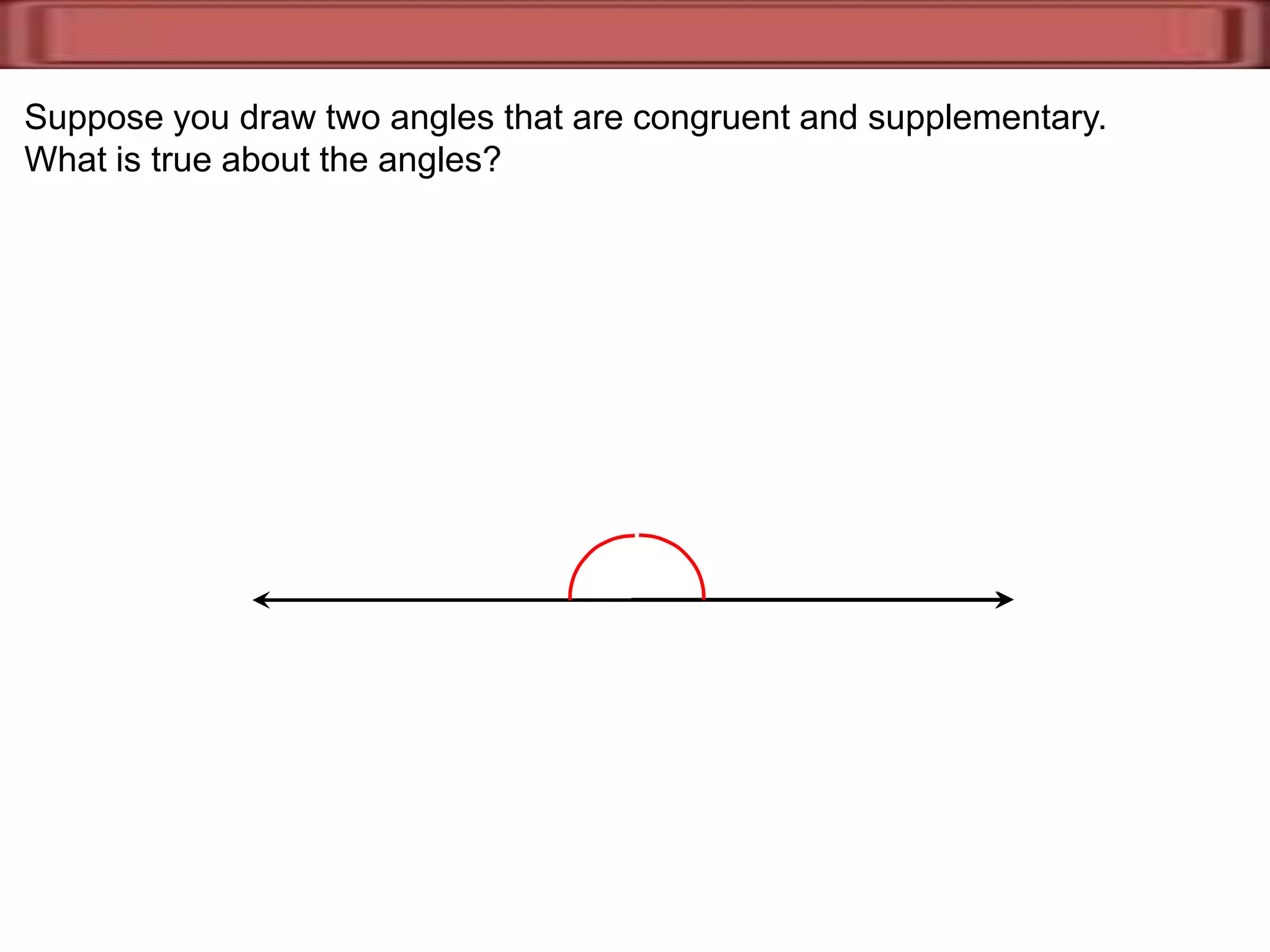
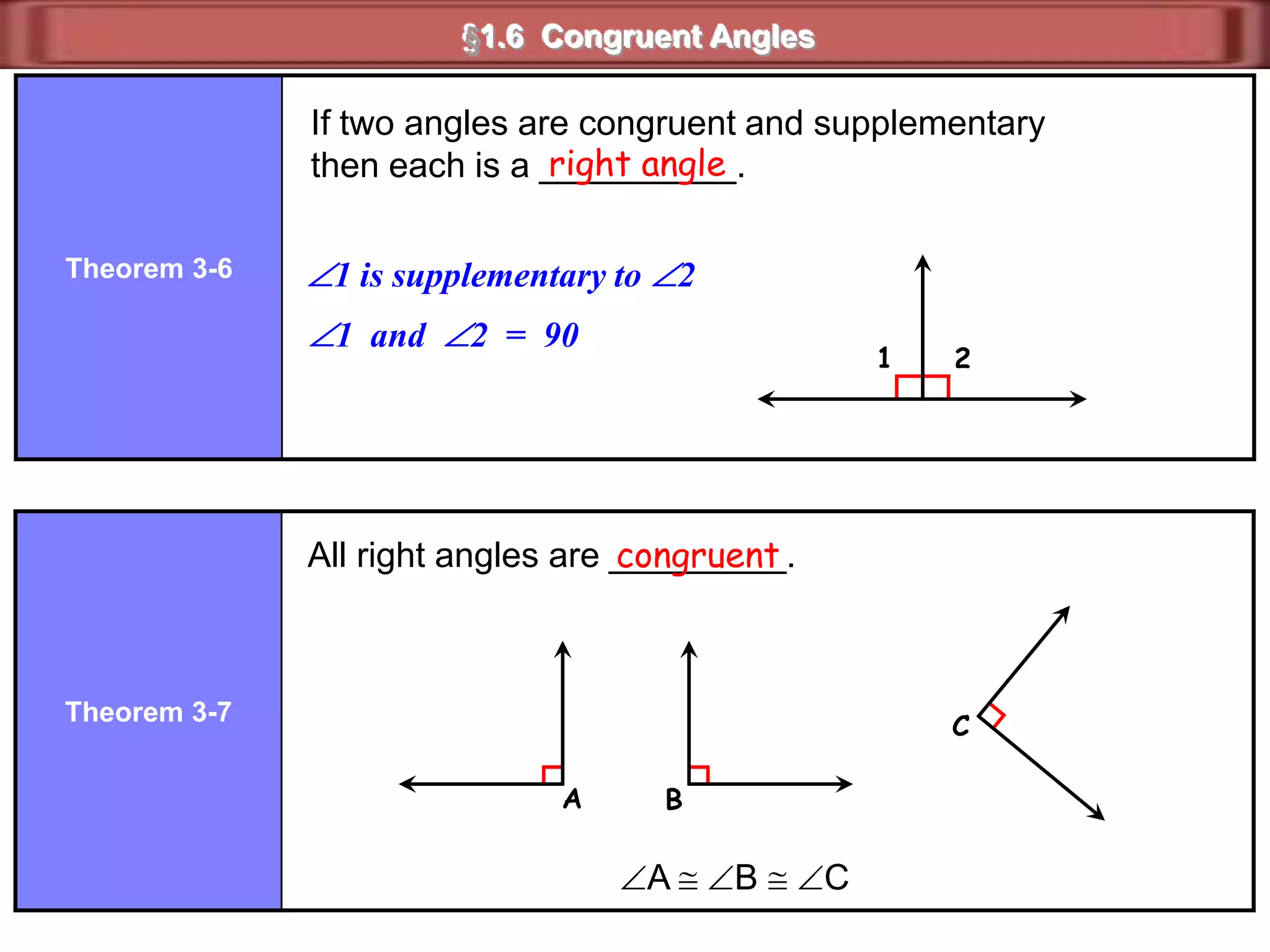
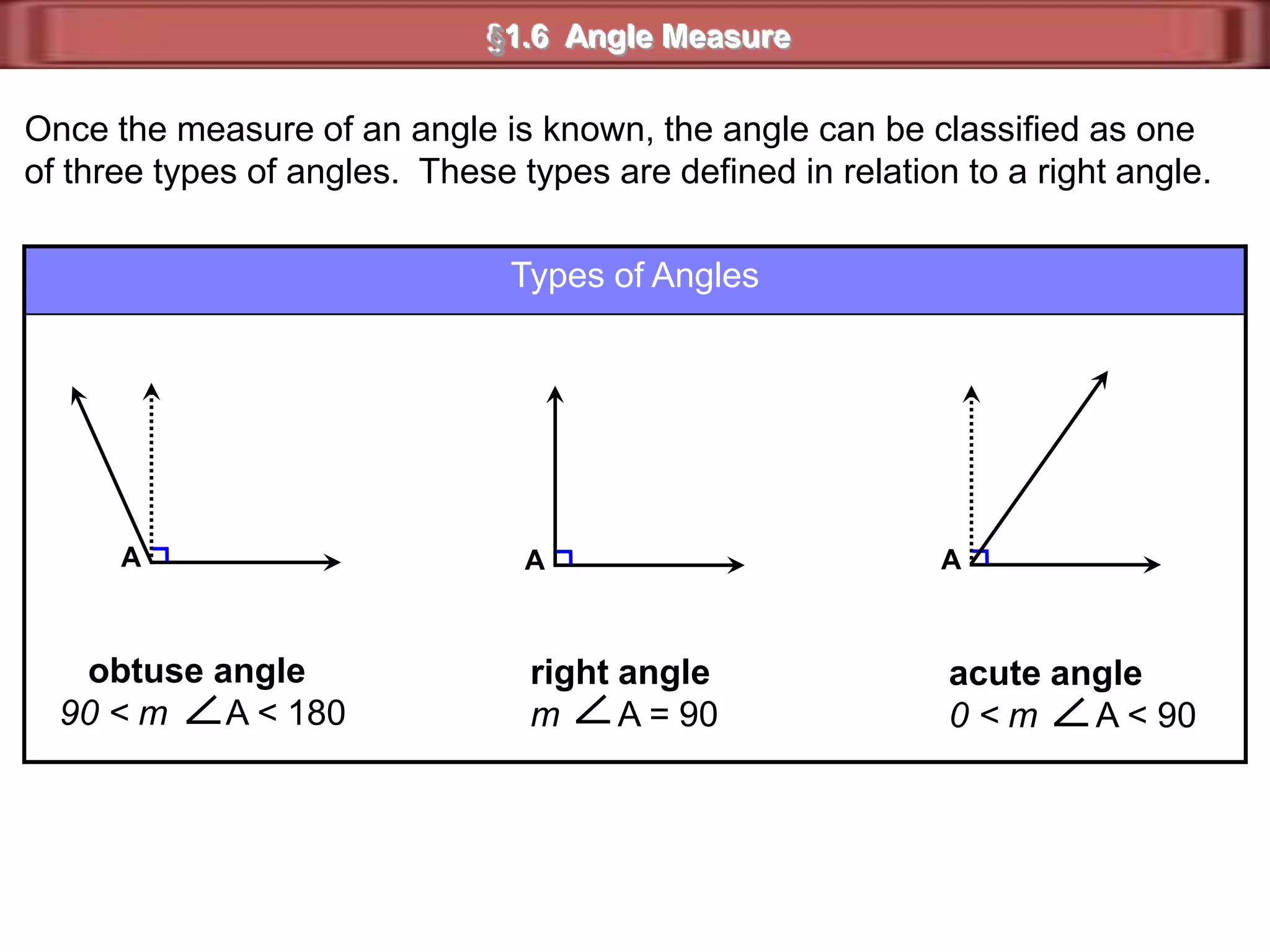
1) Complementary angles are two angles whose measures sum to 90 degrees. They do not need to share a vertex or side. 2) Supplementary angles are two angles whose measures sum to 180 degrees. 3) Examples show complementary angles with measures summing to 90 degrees and supplementary angles with measures summing to 180 degrees.

1. Angles§1.6Angles

2. §1.6Angle Measure

3. §1.6The Angle Addition Postulate

4. §1.6Adjacent Angles and Linear Pairs of Angles

5. §1.6Complementary and Supplementary Angles

6. §1.6Congruent Angles

7. §1.6 Perpendicular LinesVocabularyAnglesWhat You'll LearnYou will learn to name and identify parts of an angle.1) Opposite Rays2) Straight Angle3)Angle4) Vertex5) Sides6) Interior7) Exterior

8. ZYXY and XZ are ____________.XAnglesOpposite rays___________ are two rays that are part of a the same line and have only theirendpoints in common.opposite raysstraight angleThe figure formed by opposite rays is also referred to as a ____________.

9. SvertexTAnglesThere is another case where two rays can have a common endpoint.angleThis figure is called an _____.Some parts of angles have special names.The common endpoint is called the ______,vertexand the two rays that make up the sides ofthe angle are called the sides of the angle.sideRside

10. SvertexSRTTRSR1TAnglesThere are several ways to name this angle.1) Use the vertex and a point from each side. orThe vertex letter is always in the middle.side2) Use the vertex only.1If there is only one angle at a vertex, then theangle can be named with that vertex.Rside3) Use a number.

11. D2FDEF2EFEDEAnglesSymbols:

12. CA1BABC1BCBABA andBCAngles1) Name the angle in four ways.2) Identify the vertex and sides of this angle.vertex:Point Bsides:

13. 2) What are other names for ?3) Is there an angle that can be named ? 121XWY orYWXWXWZAngles1) Name all angles having W as their vertex.XW12YZNo!

14. exteriorWYZinteriorABAnglesAn angle separates a plane into three parts:interior1) the ______exterior2) the ______angle itself 3) the _________In the figure shown, point B and all other points in the blue region are in the interiorof the angle.Point A and all other points in the greenregion are in the exterior of the angle.Points Y, W, and Z are on the angle.

15. PGAnglesIs point B in the interior of the angle, exterior of the angle, or on the angle?ExteriorBIs point G in the interior of the angle, exterior of the angle, or on the angle?On the angleIs point P in the interior of the angle, exterior of the angle, or on the angle?Interior

16. Vocabulary§1.6 Angle MeasureWhat You'll LearnYou will learn to measure, draw, and classify angles.1) Degrees2) Protractor3)Right Angle4) Acute Angle5) Obtuse Angle

17. P75°QRm PQR = 75§1.6 Angle MeasuredegreesIn geometry, angles are measured in units called _______.The symbol for degree is °.In the figure to the right, the angle is 75 degrees.In notation, there is no degree symbol with 75because the measure of an angle is a real number with no unit of measure.

18. An°Cm ABC = nand 0 < n < 180B§1.6 Angle Measure0180

19. Use a protractor to measure SRQ.1) Place the center point of the protractor on vertex R. Align the straightedge with side RS.2) Use the scale that begins with 0 at RS. Read where the other side of the angle, RQ, crosses this scale.QRS§1.6 Angle MeasureprotractorYou can use a _________ to measure angles and sketch angles of givenmeasure.

20. m SRQ = m SRJ = m SRG = m QRG = m GRJ = m SRH HJGQSR§1.6 Angle Measure70Find the measurement of: 180 – 150= 3018045 150 – 45= 105150

21. 1) Draw AB3) Locate and draw point C at the mark labeled 135. Draw AC.CAB§1.6 Angle MeasureUse a protractor to draw an angle having a measure of 135.2) Place the center point of the protractor on A. Align the mark labeled 0 with the ray.

22. AAA obtuse angle 90 < m A < 180acute angle 0 < m A < 90right angle m A = 90§1.6 Angle MeasureOnce the measure of an angle is known, the angle can be classified as oneof three types of angles. These types are defined in relation to a right angle.

23. 40°110°90°50°75°130°§1.6 Angle MeasureClassify each angle as acute, obtuse, or right.AcuteObtuseRightObtuseAcuteAcute

24. The measure of H is 67.Solve for y.The measure of B is 138.Solve for x.H 9y + 45x - 7B B = 5x – 7 and B = 138H = 9y + 4 and H = 67§1.6 Angle MeasureGiven: (What do you know?)Given: (What do you know?)9y + 4 = 675x – 7 = 138Check!Check!9y = 635x = 1459(7) + 4 = ?5(29) -7 = ?y = 7x = 2963 + 4 = ?145 -7 = ?67 = 67138 = 138

25. Is m a larger than m b ?? ? ?60°60°

26. End of Lesson

27. Vocabulary§1.6 The Angle Addition PostulateWhat You'll LearnYou will learn to find the measure of an angle and the bisectorof an angle. NOTHING NEW!

28. RX2) Draw and label a point X in the interior of the angle. Then draw SX.ST§1.6 The Angle Addition Postulate1) Draw an acute, an obtuse, or a right angle. Label the angle RST.45°75°30°3) For each angle, find mRSX, mXST, and RST.

29. RXST§1.6 The Angle Addition Postulate1) How does the sum of mRSX and mXST compare to mRST ?Their sum is equal to the measure of RST .mXST = 30+ mRSX = 45= mRST = 752) Make a conjecture about the relationship between the two smaller angles and the larger angle.45°The sum of the measures of the twosmaller angles is equal to the measureof the larger angle.75°30°

30. P1QA2R§1.6 The Angle Addition Postulatem1 + m2 = mPQR.There are two equations that can be derived using Postulate 3 – 3.m1 = mPQR –m2 These equations are true no matter where A is locatedin the interior of PQR. m2 = mPQR –m1

31. X1YW2Z§1.6 The Angle Addition PostulateFind m2 if mXYZ = 86 and m1 = 22.Postulate 3 – 3.m2 + m1 = mXYZm2 = mXYZ –m1 m2 = 86 – 22m2 = 64

32. CD(5x – 6)°2x°BA§1.6 The Angle Addition PostulateFind mABC and mCBD if mABD = 120.mABC + mCBD = mABDAngle Addition PostulateSubstitution2x + (5x – 6) = 1207x – 6 = 120Combine like terms7x = 126Add 6 to both sidesx = 18Divide each side by 736 + 84 = 120mCBD = 5x – 6 mABC = 2xmCBD = 5(18) – 6 mABC = 2(18)mCBD = 90 – 6 mABC = 36mCBD = 84

33. §1.6 The Angle Addition PostulateJust as every segment has a midpoint that bisects the segment, every anglehas a ___ that bisects the angle.rayangle bisectorThis ray is called an ____________ .

34. is the bisector of PQR.P1QA2R§1.6 The Angle Addition Postulatem1 = m2

35. Since bisects CAN, 1 = 2.NT21AC§1.6 The Angle Addition PostulateIf bisects CAN and mCAN = 130, find 1 and 2.1 + 2 = CANAngle Addition PostulateReplace CAN with 1301 + 2 = 1301 + 1 = 130Replace 2 with 12(1) = 130Combine like terms(1) = 65Divide each side by 2Since 1 = 2, 2 = 65

36. End of Lesson

37. ABDCAdjacent Angles and Linear Pairs of AnglesWhat You'll LearnYou will learn to identify and use adjacent angles and linear pairs of angles.When you “split” an angle, you create two angles. The two angles are called _____________adjacent angles21adjacent = next to, joining.1 and 2 are examples of adjacent angles. They share a common ray.Name the ray that 1 and 2 have in common. ____

38. J2common sideRM11 and 2 are adjacentwith the same vertex R andNAdjacent Angles and Linear Pairs of AnglesAdjacent angles are angles that:A) share a common sideB) have the same vertex, andC) have no interior points in common

39. B2112GNL1J2Adjacent Angles and Linear Pairs of AnglesDetermine whether 1 and 2 are adjacent angles.No. They have a common vertex B, but _____________no common sideYes. They have the same vertex G and a common side with no interior points in common.No. They do not have a common vertex or ____________a common sideThe side of 1 is ____The side of 2 is ____

40. 1212ZDXAdjacent Angles and Linear Pairs of AnglesDetermine whether 1 and 2 are adjacent angles.No. Yes. In this example, the noncommon sides of the adjacent angles form a___________.straight linelinear pairThese angles are called a _________

41. DAB21CNote:Adjacent Angles and Linear Pairs of AnglesTwo angles form a linear pair if and only if (iff):A) they are adjacent andB) their noncommon sides are opposite rays1 and 2 are a linear pair.

42. In the figure, and are opposite rays.HTE3A421CACE and 1 have a common side ,the same vertex C, and opposite rays andMAdjacent Angles and Linear Pairs of Angles1) Name the angle that forms a linear pair with 1.ACE2) Do 3 and TCM form a linear pair? Justify your answer.No. Their noncommon sides are not opposite rays.

43. End of Lesson

44. §1.6 Complementary and Supplementary AnglesWhat You'll LearnYou will learn to identify and use Complementary and Supplementary angles

45. EDA60°30°FBC§1.6 Complementary and Supplementary AnglesTwo angles are complementary if and only if (iff) the sum of their degree measure is 90. mABC + mDEF = 30 + 60 = 90

46. EDA60°30°FBC§1.6 Complementary and Supplementary AnglesIf two angles are complementary, each angle is a complement of the other.ABC is the complement of DEF and DEF is the complement of ABC.Complementary angles DO NOT need to have a common side or even the same vertex.

47. I75°15°HPQ40°50°HSUV60°T30°ZW§1.6 Complementary and Supplementary AnglesSome examples of complementary angles are shown below.mH + mI = 90mPHQ + mQHS = 90mTZU + mVZW = 90

48. DC130°50°EBFA§1.6 Complementary and Supplementary AnglesIf the sum of the measure of two angles is 180, they form a special pair of angles called supplementary angles.Two angles are supplementary if and only if (iff) the sum of their degree measure is 180. mABC + mDEF = 50 + 130 = 180

49. I75°105°HQ130°50°HSPUV60°120°60°ZWT§1.6 Complementary and Supplementary AnglesSome examples of supplementary angles are shown below.mH + mI = 180mPHQ + mQHS = 180mTZU + mUZV = 180andmTZU + mVZW = 180

50. End of Lesson

51. §1.6 Congruent AnglesWhat You'll LearnYou will learn to identify and use congruent andvertical angles.Recall that congruent segments have the same ________.measureCongruent angles_______________ also have the same measure.

52. 50°50°BV§1.6 Congruent AnglesTwo angles are congruent iff, they have the same______________.degree measureB  V iffmB = mV

53. 12XZ§1.6 Congruent AnglesarcsTo show that 1 is congruent to 2, we use ____.To show that there is a second set of congruent angles, X and Z, we use double arcs.This “arc” notation states that:X  ZmX = mZ

54. §1.6 Congruent AnglesfourWhen two lines intersect, ____ angles are formed.There are two pair of nonadjacent angles.vertical anglesThese pairs are called _____________.1423

55. §1.6 Congruent AnglesTwo angles are vertical iff they are two nonadjacentangles formed by a pair of intersecting lines.Vertical angles:1 and 31422 and 43

56. 1423§1.6 Congruent Angles1) On a sheet of paper, construct two intersecting lines that are not perpendicular.2) With a protractor, measure each angle formed.3) Make a conjecture about vertical angles.Consider:A. 1 is supplementary to 4.m1 + m4 = 180Hands-OnB. 3 is supplementary to 4.m3 + m4 = 180Therefore, it can be shown that1 3Likewise, it can be shown that24

57. 1423§1.6 Congruent Angles1) If m1 = 4x + 3 and the m3 = 2x + 11, then find the m3x = 4; 3 = 19°2) If m2 = x + 9 and the m3 = 2x + 3, then find the m4x = 56; 4 = 65°3) If m2 = 6x - 1 and the m4 = 4x + 17, then find the m3x = 9; 3 = 127°4) If m1 = 9x - 7 and the m3 = 6x + 23, then find the m4x = 10; 4 = 97°

58. §1.6 Congruent AnglesVertical angles are congruent.nm21  3312  44

59. 130°x°§1.6 Congruent AnglesFind the value of x in the figure:The angles are vertical angles.So, the value of x is 130°.

60. §1.6 Congruent AnglesFind the value of x in the figure:The angles are vertical angles.(x – 10) = 125.(x – 10)°x – 10 = 125.125°x = 135.

61. §1.6 Congruent AnglesSuppose two angles are congruent.What do you think is true about their complements?1  22 + y = 901 + x = 90y is the complement of 2x is the complement of 1y = 90 - 2x = 90 - 1Because 1  2, a “substitution” is made.y = 90 - 1x = 90 - 1x = yx  yIf two angles are congruent, their complements are congruent.

62. 60°60°BA1234§1.6 Congruent AnglesIf two angles are congruent, then their complements are_________.congruentThe measure of angles complementary to A and Bis 30.A  BIf two angles are congruent, then their supplements are_________.congruentThe measure of angles supplementary to 1 and 4is 110.110°110°70°70°4  1

63. 312§1.6 Congruent AnglesIf two angles are complementary to the same angle,then they are _________.congruent3 is complementary to 45 is complementary to 44355  3If two angles are supplementary to the same angle,then they are _________.congruent1 is supplementary to 23 is supplementary to 21  3

64. 52°52°AB§1.6 Congruent AnglesSuppose A  B and mA = 52.Find the measure of an angle that is supplementary to B.1B + 1 = 1801 = 180 – B1 = 180 – 521 = 128°

65. §1.6 Congruent AnglesIf 1 is complementary to 3, 2 is complementary to 3, and m3 = 25, What are m1 and m2 ?m1 + m3 = 90 Definition of complementary angles.m1 = 90 - m3 Subtract m3 from both sides.m1 = 90 - 25Substitute 25 in for m3.m1 = 65Simplify the right side.You solve for m2m2 + m3 = 90 Definition of complementary angles.m2 = 90 - m3 Subtract m3 from both sides.m2 = 90 - 25Substitute 25 in for m3.m2 = 65Simplify the right side.

66. GD12AC4B3EH§1.6 Congruent Angles1) If m1 = 2x + 3 and the m3 = 3x - 14, then find the m3x = 17; 3 = 37°2) If mABD = 4x + 5 and the mDBC = 2x + 1, then find the mEBCx = 29; EBC = 121°3) If m1 = 4x - 13 and the m3 = 2x + 19, then find the m4x = 16; 4 = 39°4) If mEBG = 7x + 11 and the mEBH = 2x + 7, then find the m1x = 18; 1 = 43°

67. Suppose you draw two angles that are congruent and supplementary.What is true about the angles?

68. 12CAB§1.6 Congruent AnglesIf two angles are congruent and supplementary then each is a __________.right angle1 is supplementary to 21 and 2 = 90All right angles are _________.congruentA  B  C

69. BA2E314CD§1.6 Congruent AnglesIf 1 is supplementary to 4, 3 is supplementary to 4, andm 1 = 64, what are m 3 and m 4?They are vertical angles.1  3m 1 = m3m 3 = 643 is supplementary to 4GivenDefinition of supplementary.m3 + m4 = 18064 + m4 = 180m4 = 180 – 64m4 = 116

70. End of Lesson

71. §1.6 Perpendicular LinesWhat You'll LearnYou will learn to identify, use properties of, and constructperpendicular lines and segments.

72. In the figure below, lines are perpendicular.A12CD43B§1.6 Perpendicular Linesperpendicular linesLines that intersect at an angle of 90 degrees are _________________.

73. mn§1.6 Perpendicular LinesPerpendicular lines are lines that intersect to form aright angle.

74. 1243§1.6 Perpendicular LinesIn the figure below, l m. The following statements are true.mlDefinition of Perpendicular Lines1) 1 is a right angle.Vertical angles are congruent2) 1  3.Definition of Linear Pair3) 1 and 4 form a linear pair.Linear pairs are supplementary4) 1 and 4 are supplementary.5) 4 is a right angle.m4 + 90 = 180, m4 = 90Vertical angles are congruent6) 2 is a right angle.

75. a1243b§1.6 Perpendicular LinesIf two lines are perpendicular, then they form four rightangles.

76. §1.6 Perpendicular Lines1) PRN is an acute angle.False.2) 4  8True

77. mT§1.6 Perpendicular LinesIf a line m is in a plane and T is a point in m, then thereexists exactly ___ line in that plane that is perpendicular tom at T.one

78. Homework: p. 40-42 (2-46even, 50-56 all)