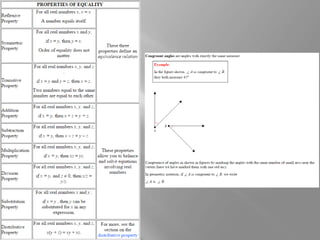
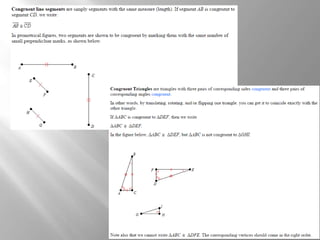
Algebraic properties of equality, such as the additive, multiplicative, and substitution properties, can be used when solving problems in geometry. These properties are accepted as true in geometry, just as certain postulates and properties are. Properties of congruence between geometric objects follow similar rules to the properties of equality between numbers. Two-column proofs in geometry are structured with statements in one column and reasons or justifications in the other column, citing given information, definitions, theorems, or postulates.

2. Algebraic properties of equality are used in
Geometry.
–Will help you solve problems and justify each step.
In Geometry, you accept postulates and properties as true.
–Some of the properties you accept as true are the properties of equality
from Algebra.
Properties of Equality
Let a, b, and c be any real numbers.
Addition Property: If a = b, then a + c = b + c.
Subtraction Property: If a = b, then a - c = b - c.
Multiplication Property: If a = b, then a * c = b * c.
Division Property: If a = b and c ≠ 0, then a/c = b/c.
Reflexive Property: a = a.
Symmetric Property: If a = b, then b = a.
Transitive Property: If a = b and b = c, then a = c.
Substitution Property: If a = b, then b can replace a in any expression.

3. Distributive Property
Use multiplication to distribute a to each term of the sum or difference
within the parentheses.
Sum: a (b + c) = ab + ac
Difference: a (b – c) = ab – ac

4. Properties of Congruence
The following are the properties of congruence. Some
textbooks list just a few of them, others list them all. These are
analogous to the properties of equality for real numbers. Here
we show congruence of angles, but the properties apply just as
well for congruent segments, triangles, or any other geometric
object.

7. Writing Two Column Proofs
A two column proof is a proof in which has to be written using two-columns,
obviously. In one column you have to have a statement and in the other
column you have to have a reason. This is the structure you use in order to
do a 2 column proof.
What I mean by information given, is that they will give you a "given"
statement and a "prove" statement.
Given is what you are starting with and what your first statement be. Prove
is what you have to prove throughout the proof, this should be the last part
of the 2 column-proof.

8. Statement: Is the problem you conclude from the proof. Is what
you have to give a name to. It's the what part of the proof.
Reason: Is the theorem or postulate you give in order to give a
name for the statement. It's the why part of the proof.
You write a 2 column-proof by drawing 2 columns. The first column
with a statement and the other with a reason. This is the structure you
have to follow in order to draw a nice 2 column proof. You have to
name the theorems and the postulates to give a reason.

9. EXAMPLES:
Given: <1 congruence <4
Prove: <2 congruence <3
Statements: Reason:
1. <1 congruence <4 1. Given
2. <1 congruence <2 and <3 congruence <4 2. Vert. <s theorem.
3. <2 congruence <4 3. Transitive.
Property of congruence
4. <2 congruence <3 4. Transitive.
Property of congruence
Given: <LXN is a right angle
Prove: <1 and <2 are complementary
Statement: Reason:
1. <LXN= 90 degrees 1. Given
2. m<LXN=90 2. Def. of right angles
3. m<1 + m<2=m<LXN 3. Angle Addition Postulate.
(AAP)
4.) m<1 + m<2=90 4. Substitution
5. <1 and <2= complementary 5. definition of complementary

10. Given: BD bisects
Prove: 2m<1 = m<ABC
Statement: Reason:
1. BD bisects <ABC 1. Given
2. <1 cong. <2 2. Def. Bisect
3. m<1+m<2=m<ABC 3. Angle Addition Bisects
4. m<1 cong. m<2 4. Def. of Congruent
5. m<1 + m<1= m<ABC 5. Substitution
6. 2m<1=m<ABC 6. Simplify
6. 2 m<1 = m<ABC
Given : <1 and <2 form a linear pair
Prove: <1 and <2 are supplementary
1. <1 and <2 form a linear pair. 1. Given
2. -> BA and -> BC form a line. 2. Def. of. linear pair
3. m<ABC = 180* 3. Def. of straight angle
4. m<AB + m<BC = m<ABC 4. Angle addition postulate
5. <1 + <2 = 180* 5. Substitution
6. <1 and <2 are supplementary 6. Def. of supplementary

11. Given: m<LAN = 30*, m<1 = 15*
Prove: -> AM bisects <LAN
1) m<LAN = 30*, m<1 = 15* 1. Given
2) m<1 + m<2 = m<LAN 2. Angle addition postulate
3) m<1 + m<2 = 30*, 15* + m<2 = 30* 3. Substitution
4) m<2 = 15* 4. Subtraction
5) m<2 = m<1 5. Transitive
6) m<2 =~ m<1 6. Def. of Congruence
7) AM bisects <LAN 7. Def. of bisect
Given: <2 =~ <3
Prove: <1 and <3 are supplementary
1) <2 =~ <3 1. Given
2) m<2 = m<3 2. Congruent supp. theorem
3) <1 and <2 form a linear pair 3. Linear pair theorem
4) m<1 + m<2 = 180* 4. Def. of a supp. angle
5) m<1 + m<3 = 180* 5. Def. of. supplementary
6) <1 and <3 are supplementary 6. Def. of. supplementary

12. All rights belong to their respective owners.
Copyright Disclaimer Under Section 107 of the Copyright Act 1976,
allowance is made for "fair use" for purposes such as criticism, comment,
news reporting, TEACHING, scholarship, and research.
Fair use is a use permitted by copyright statute that might otherwise be
infringing.
Non-profit, EDUCATIONAL or personal use tips the balance in favor of
fair use.