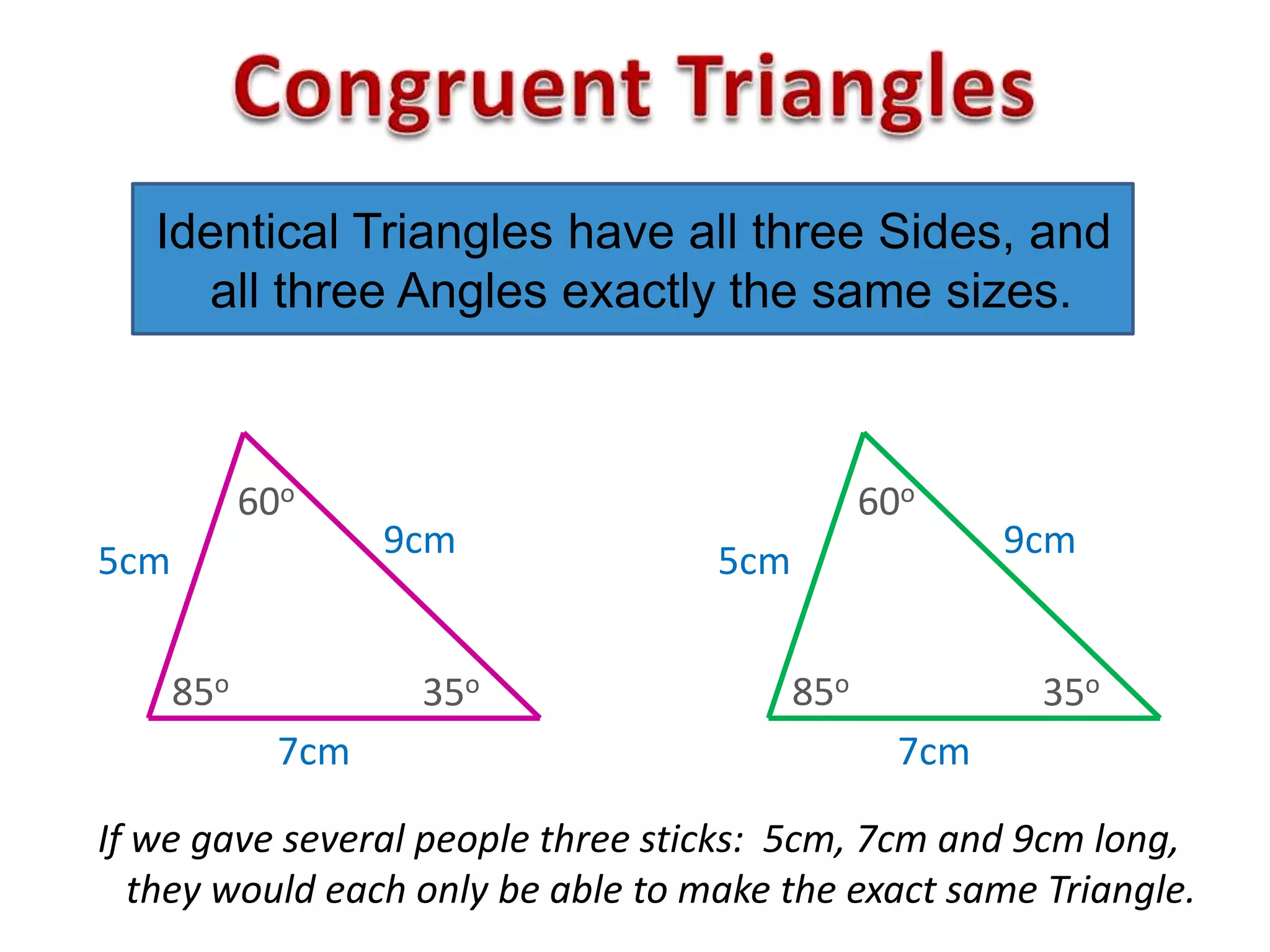
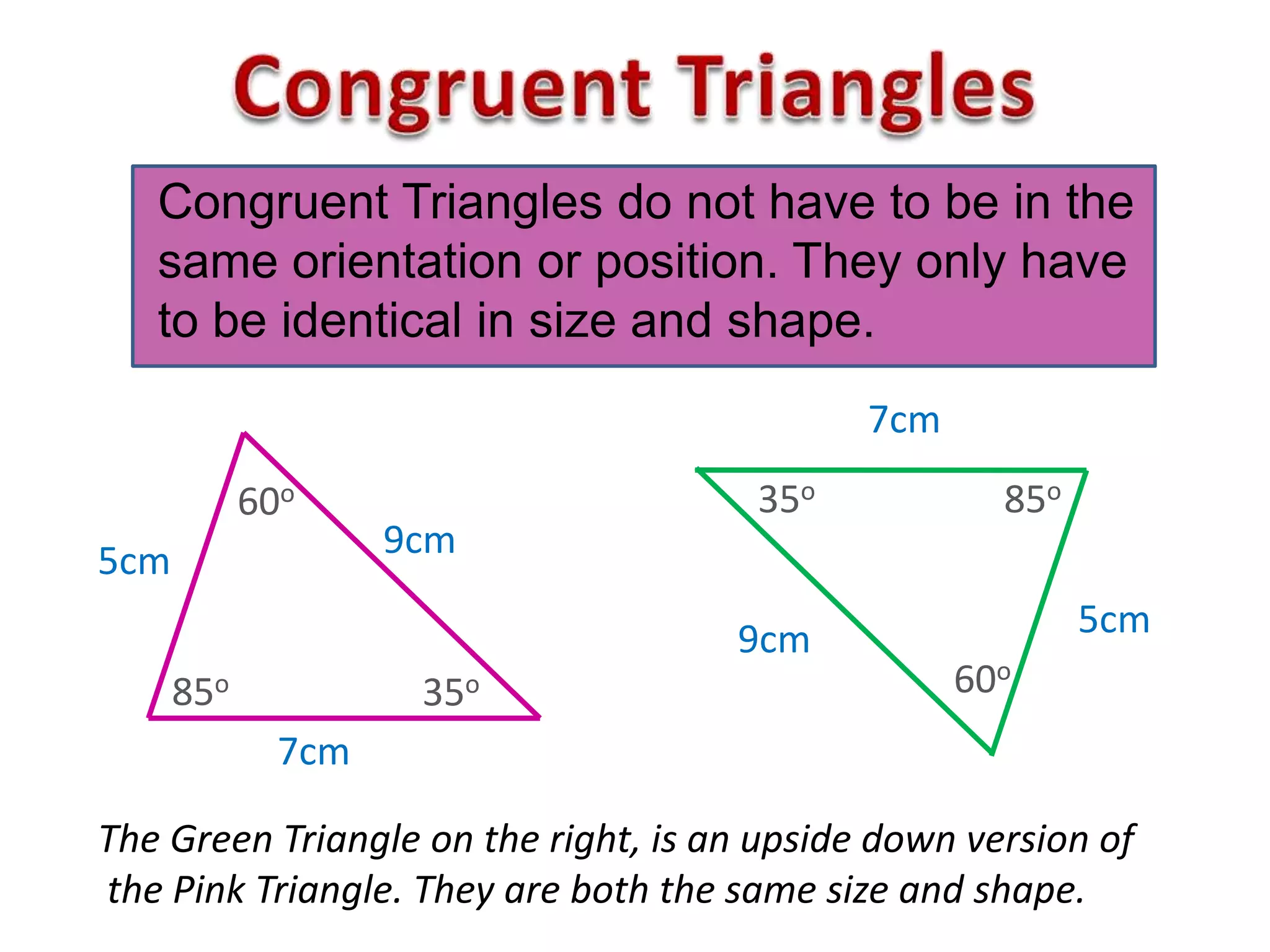
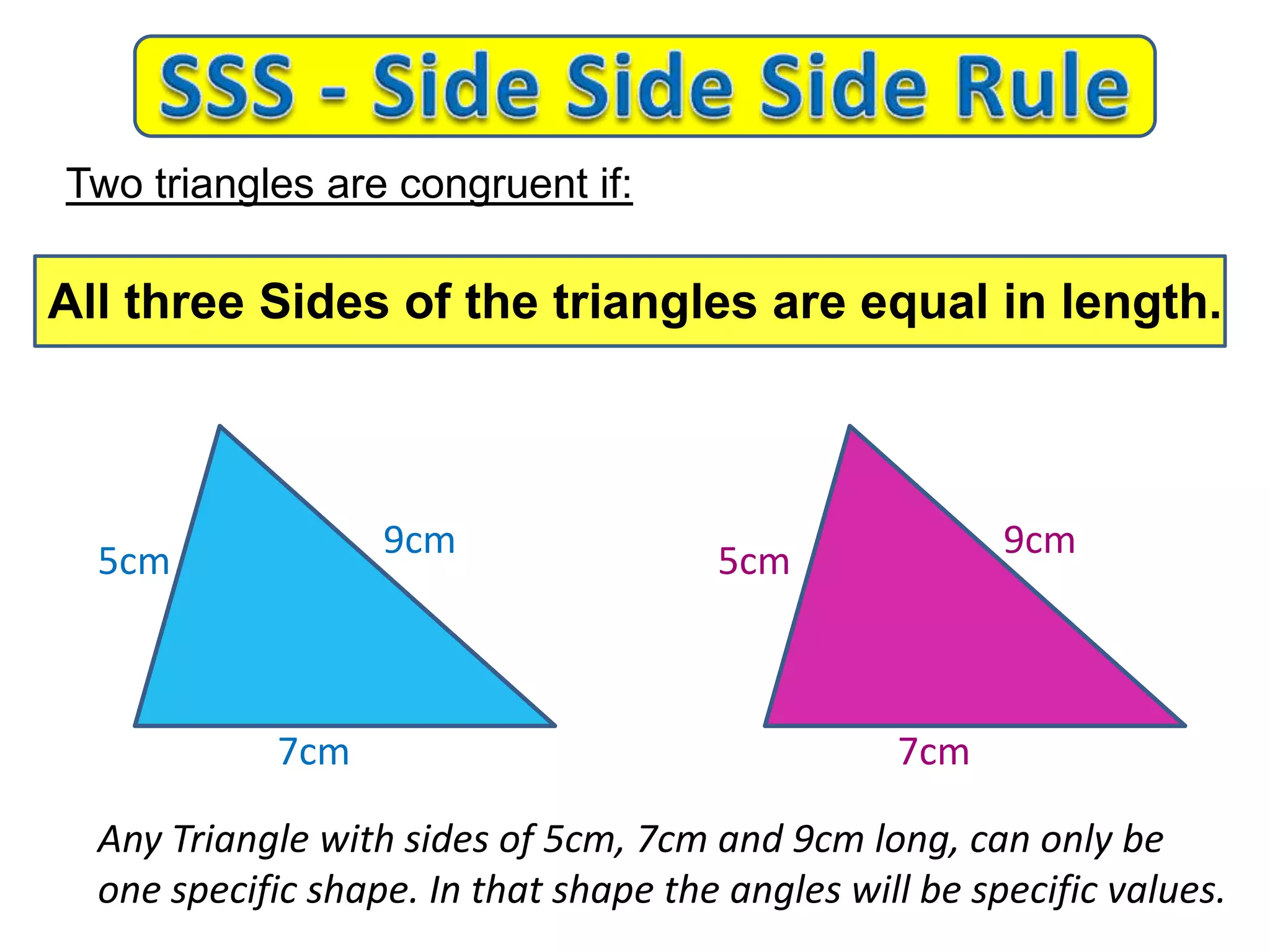
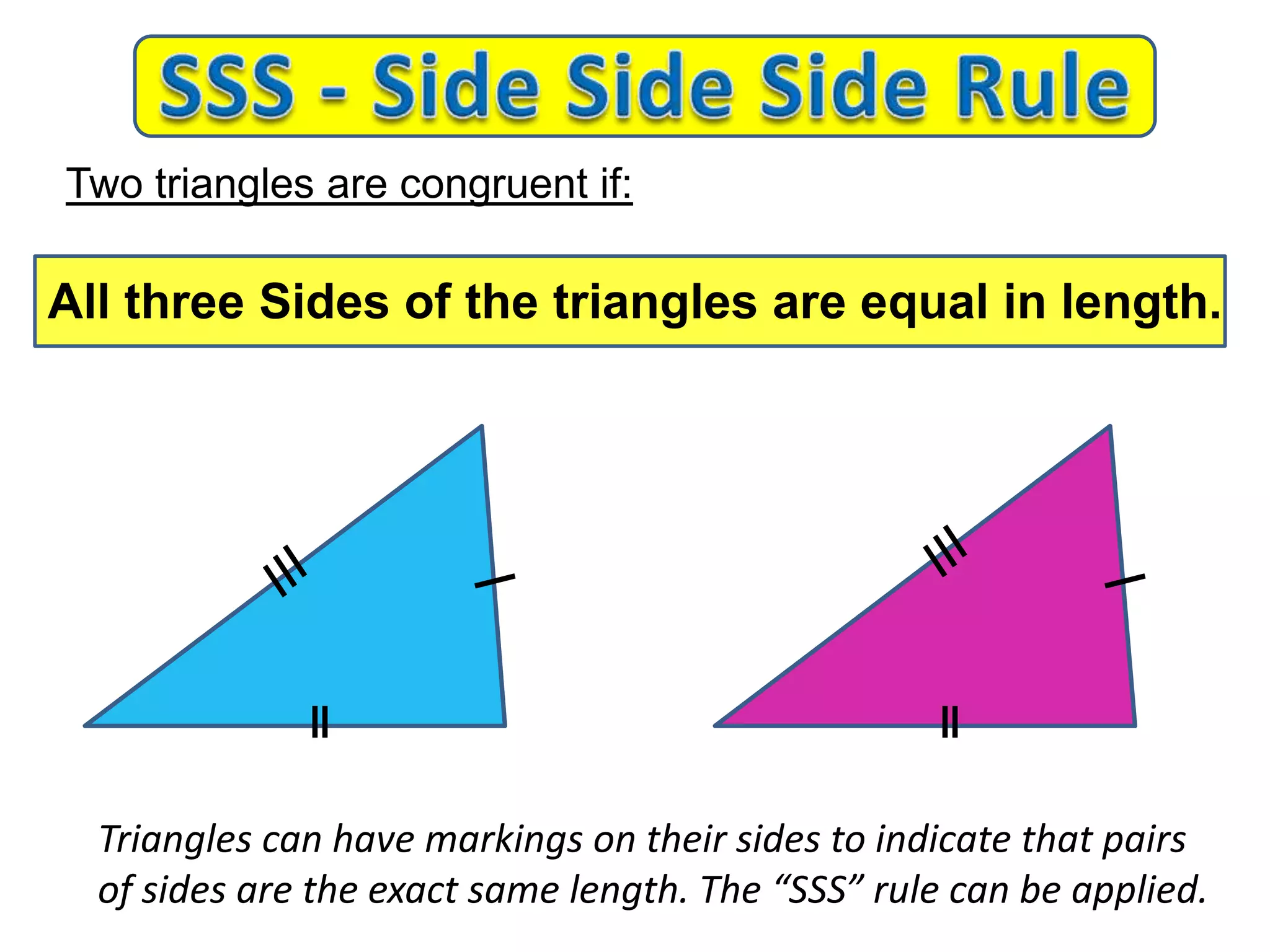
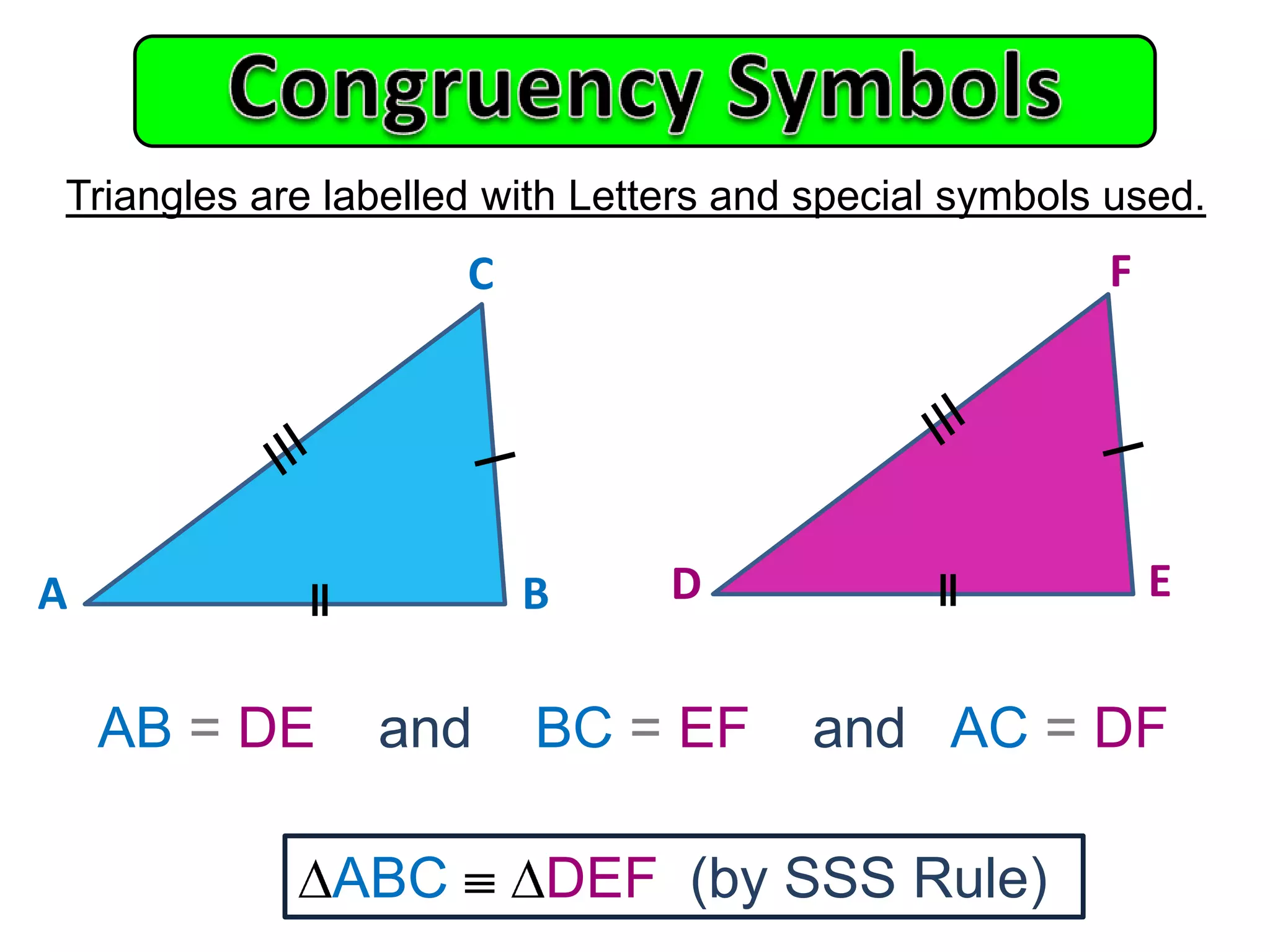
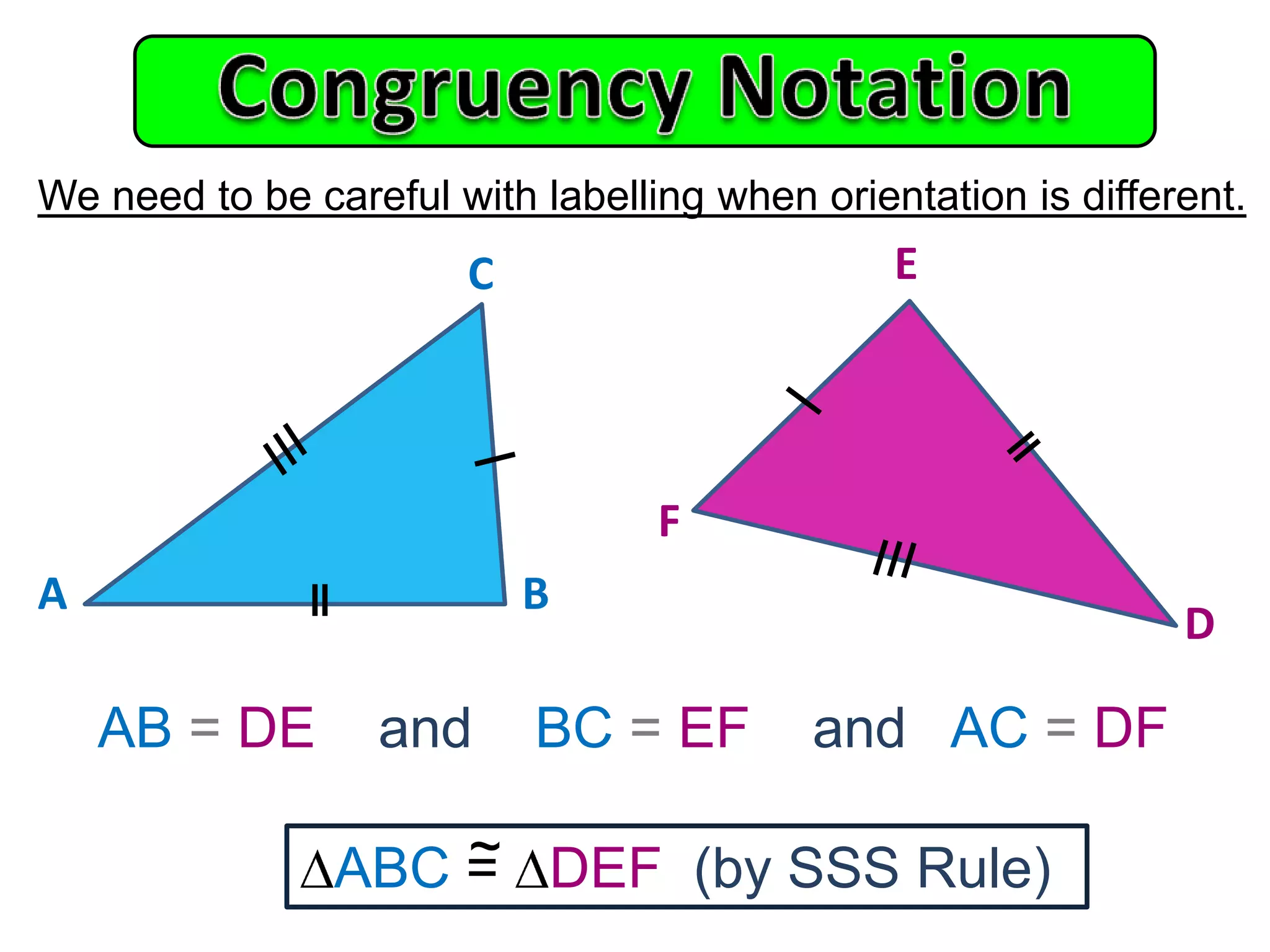
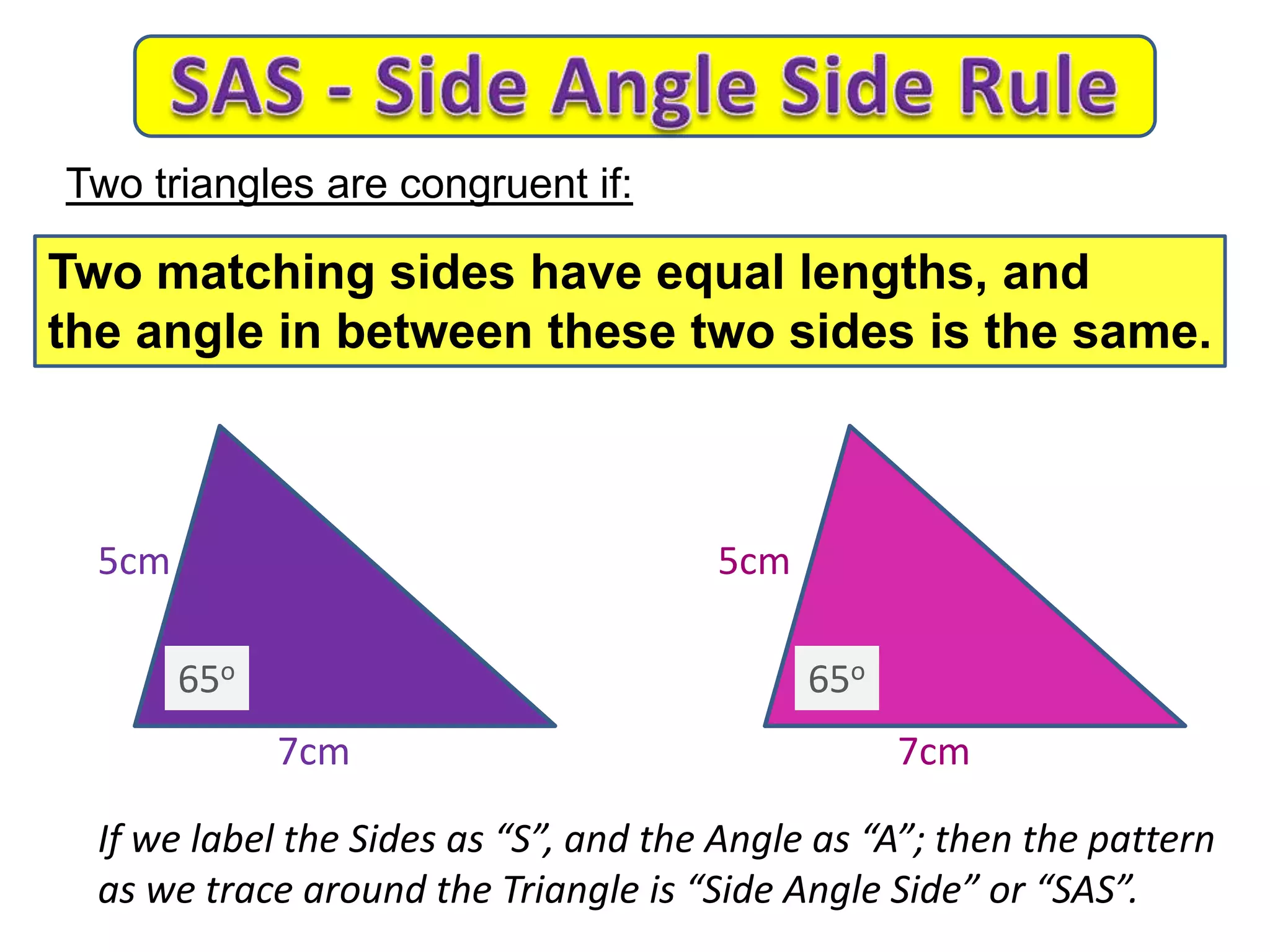
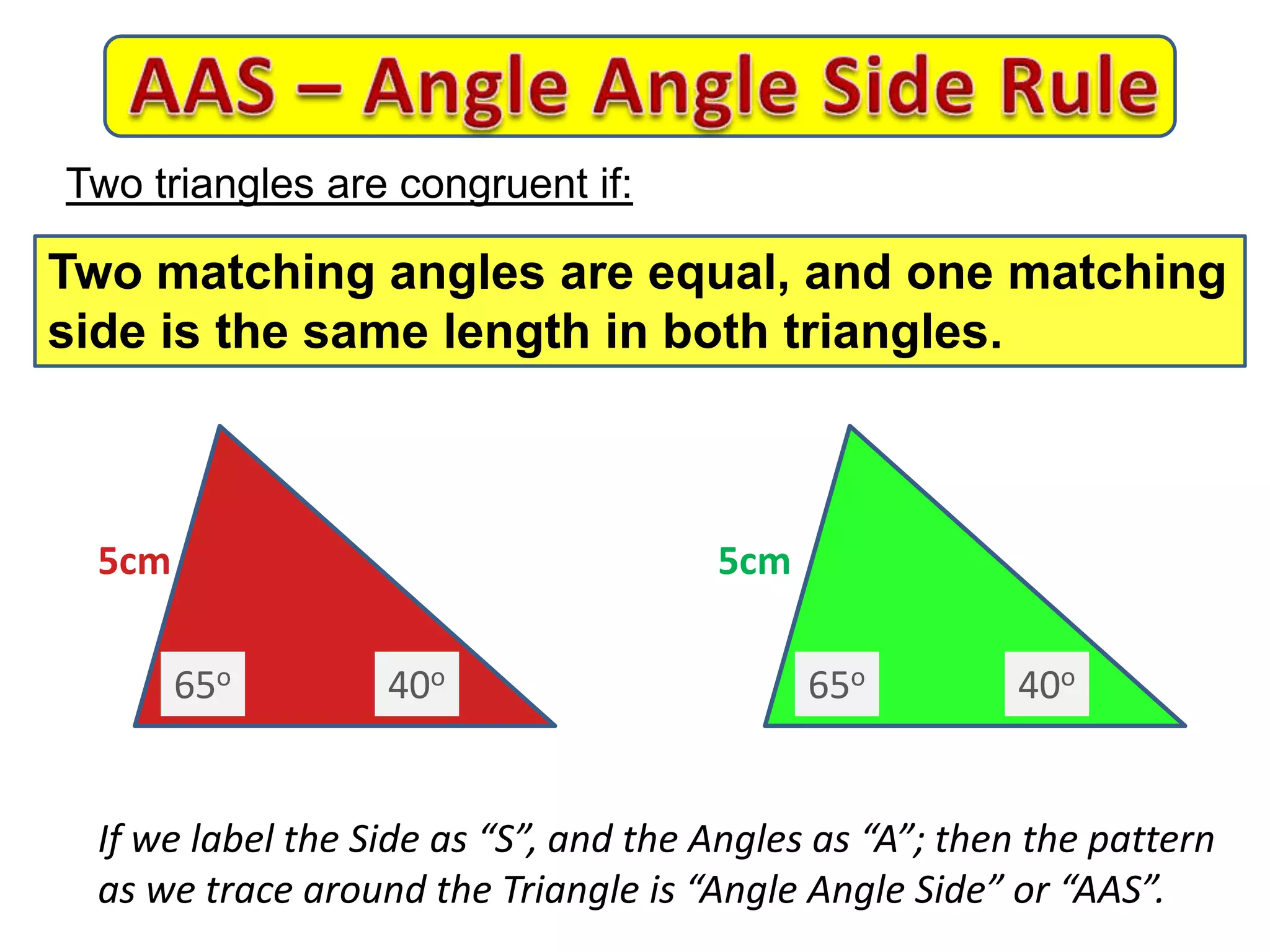
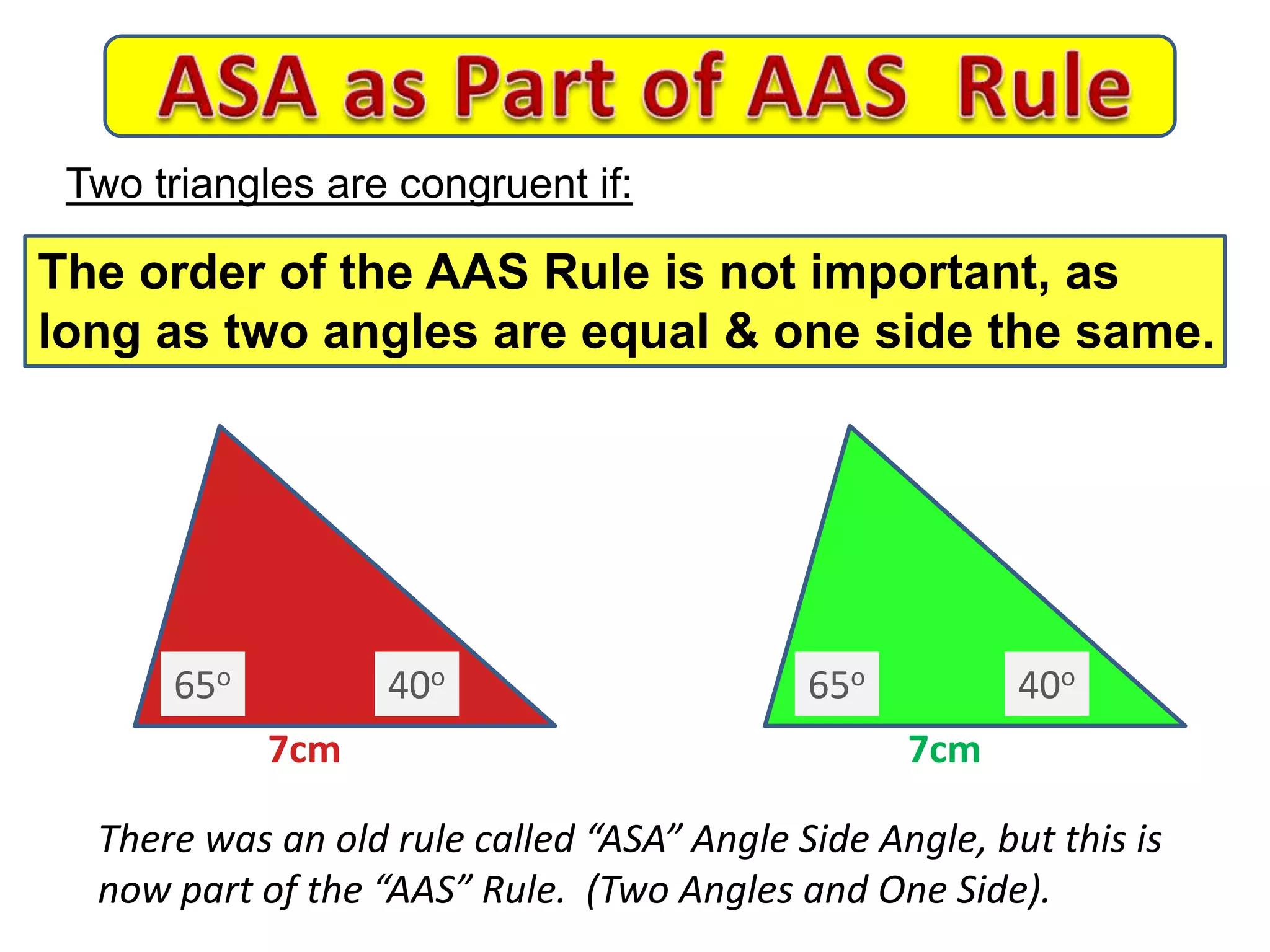
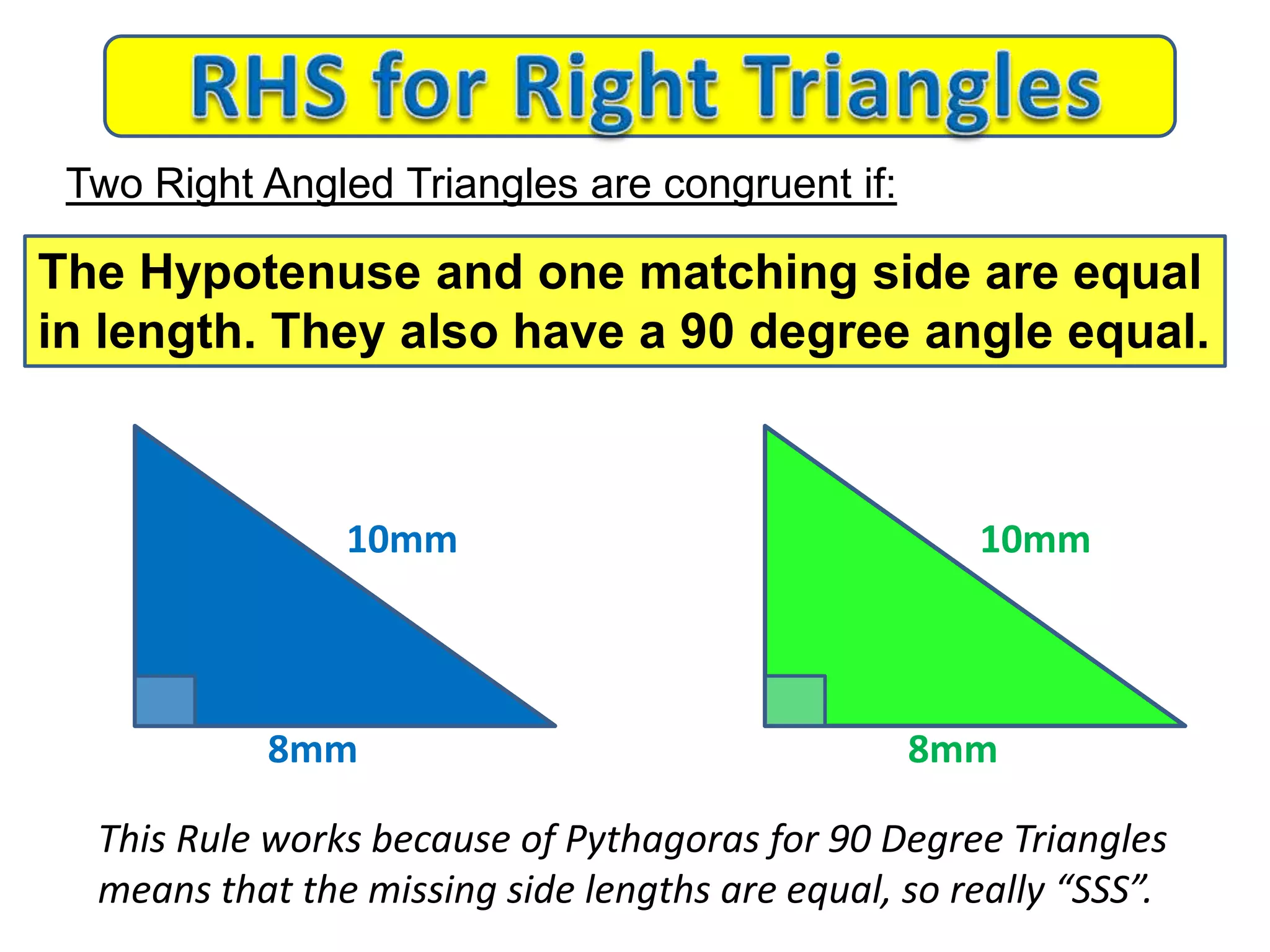
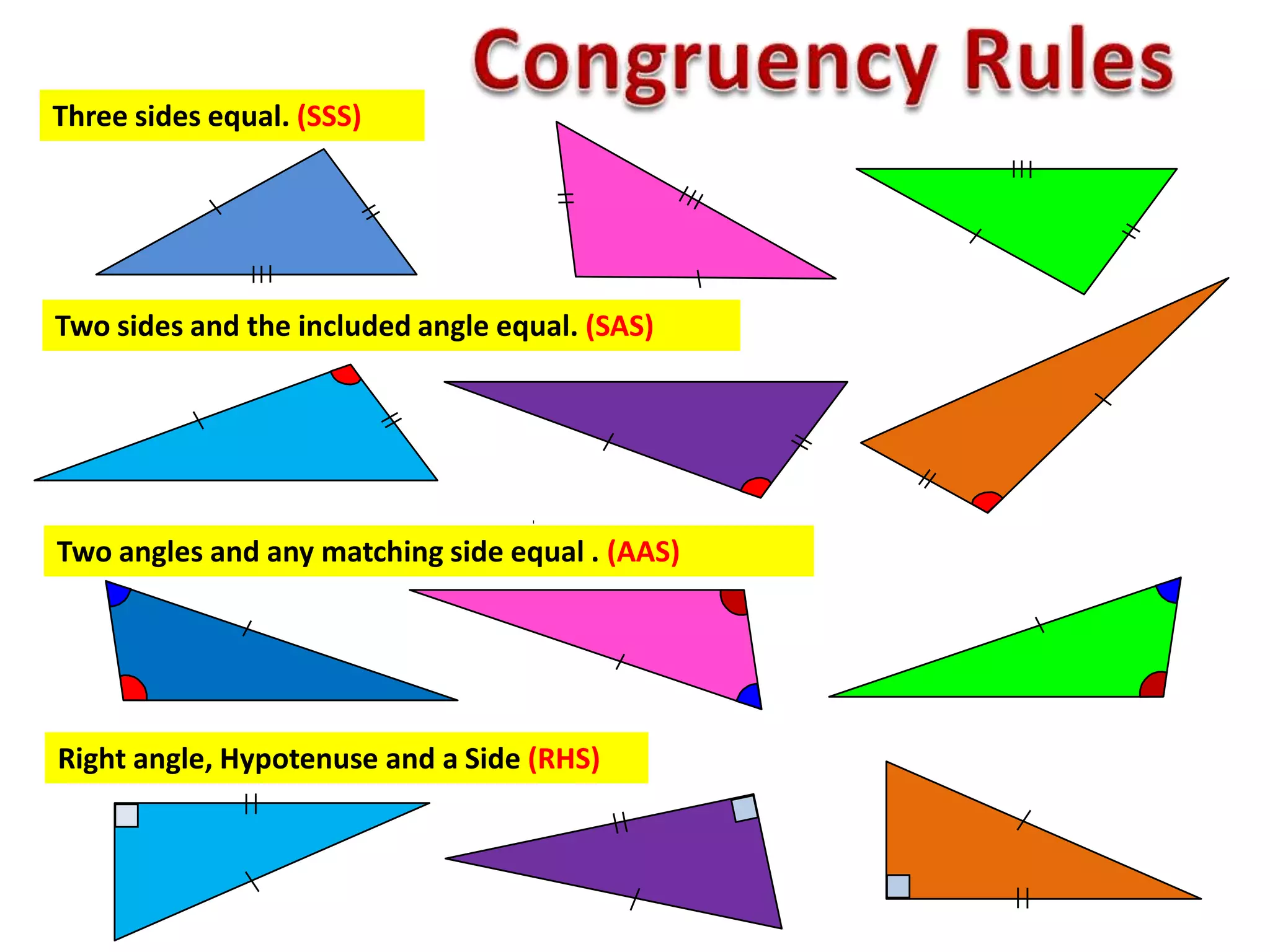
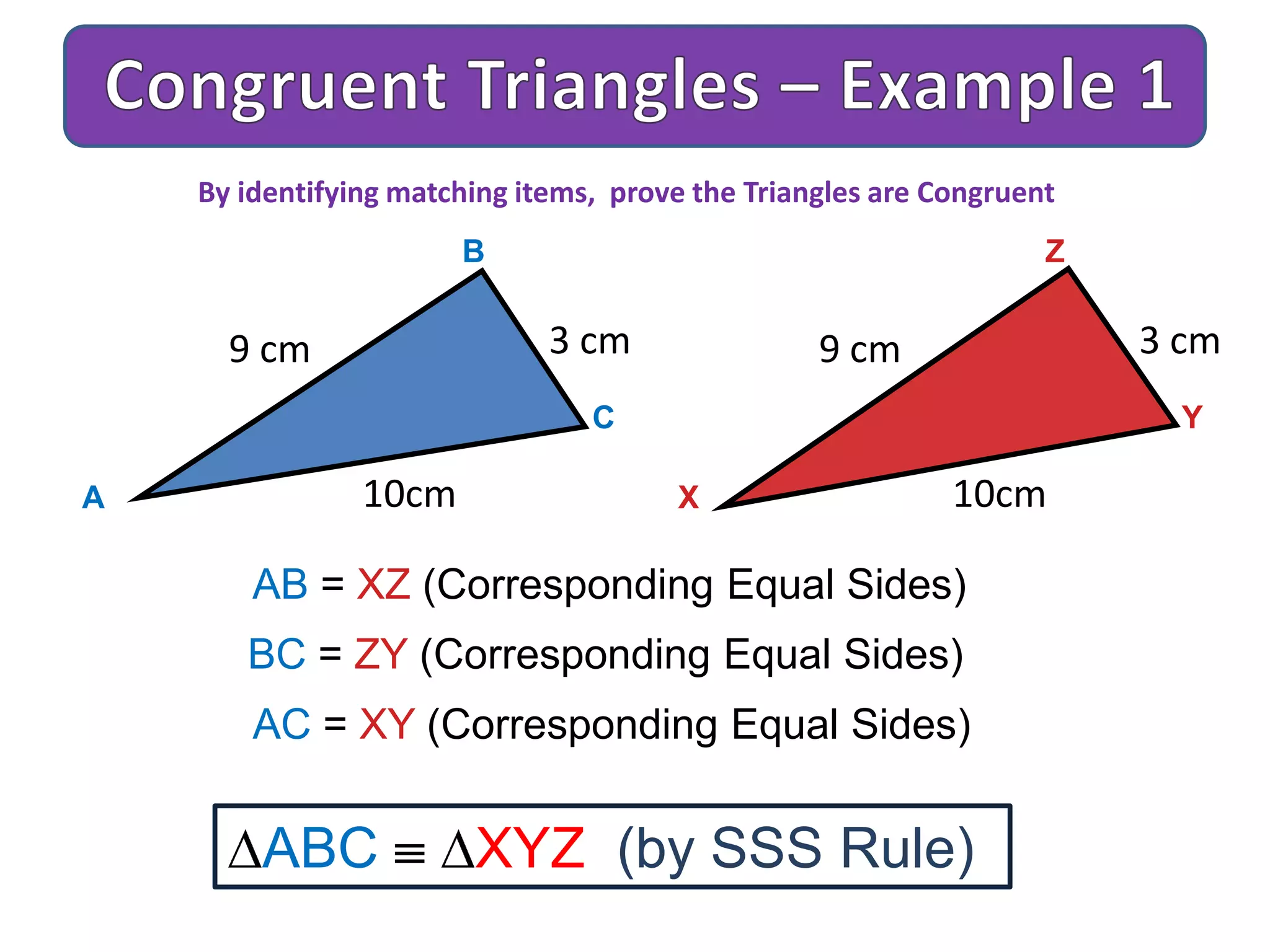
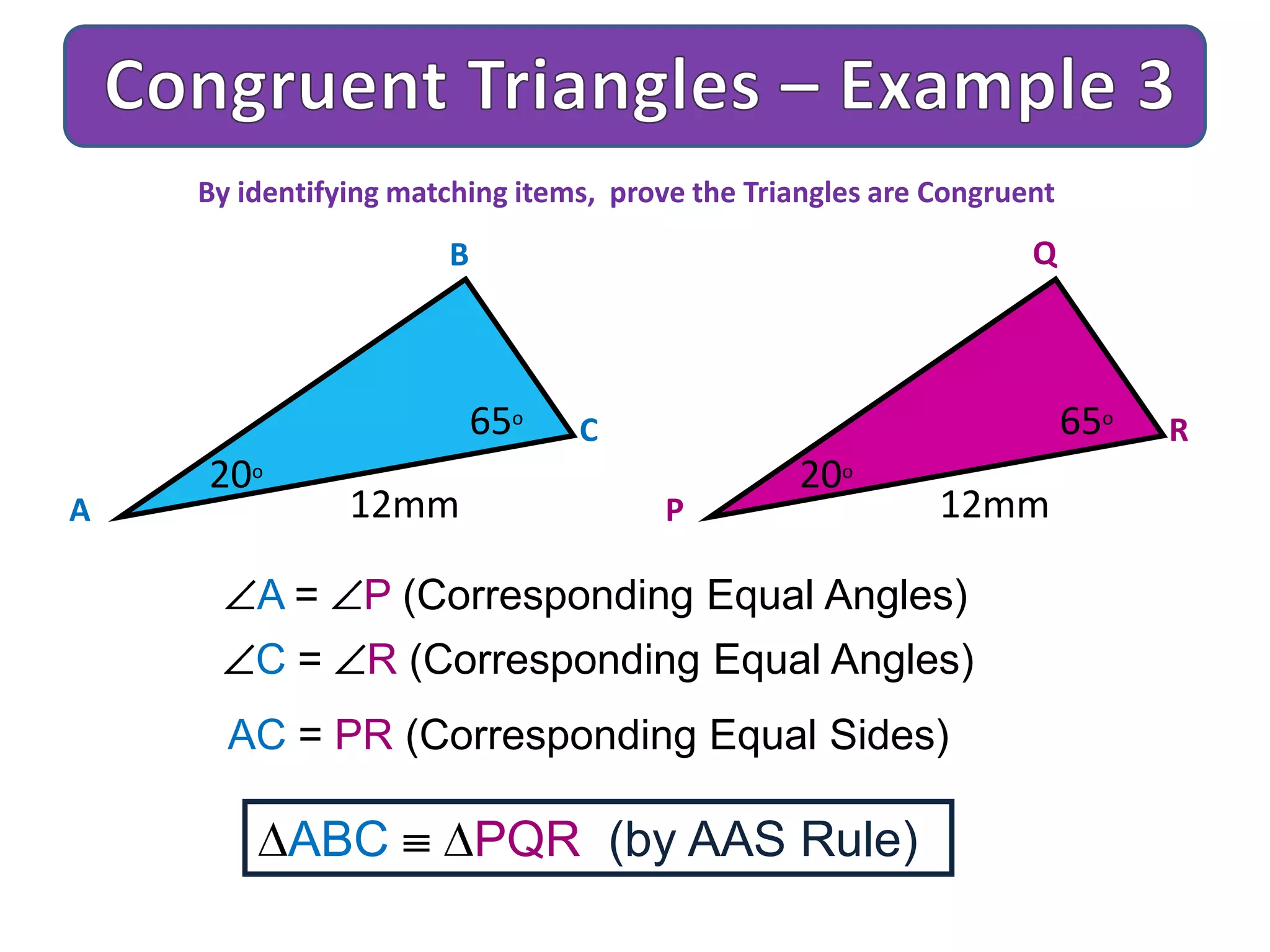
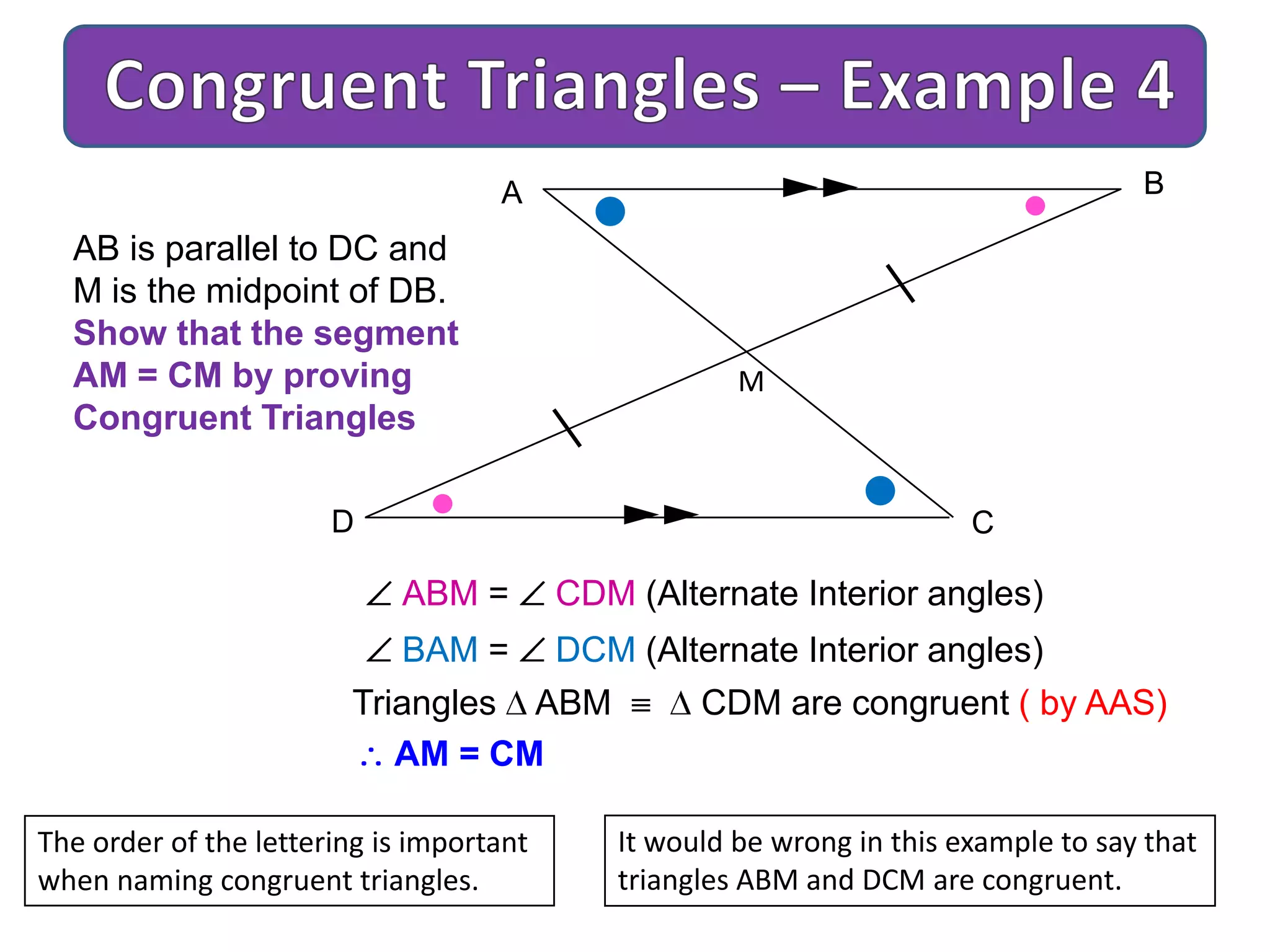
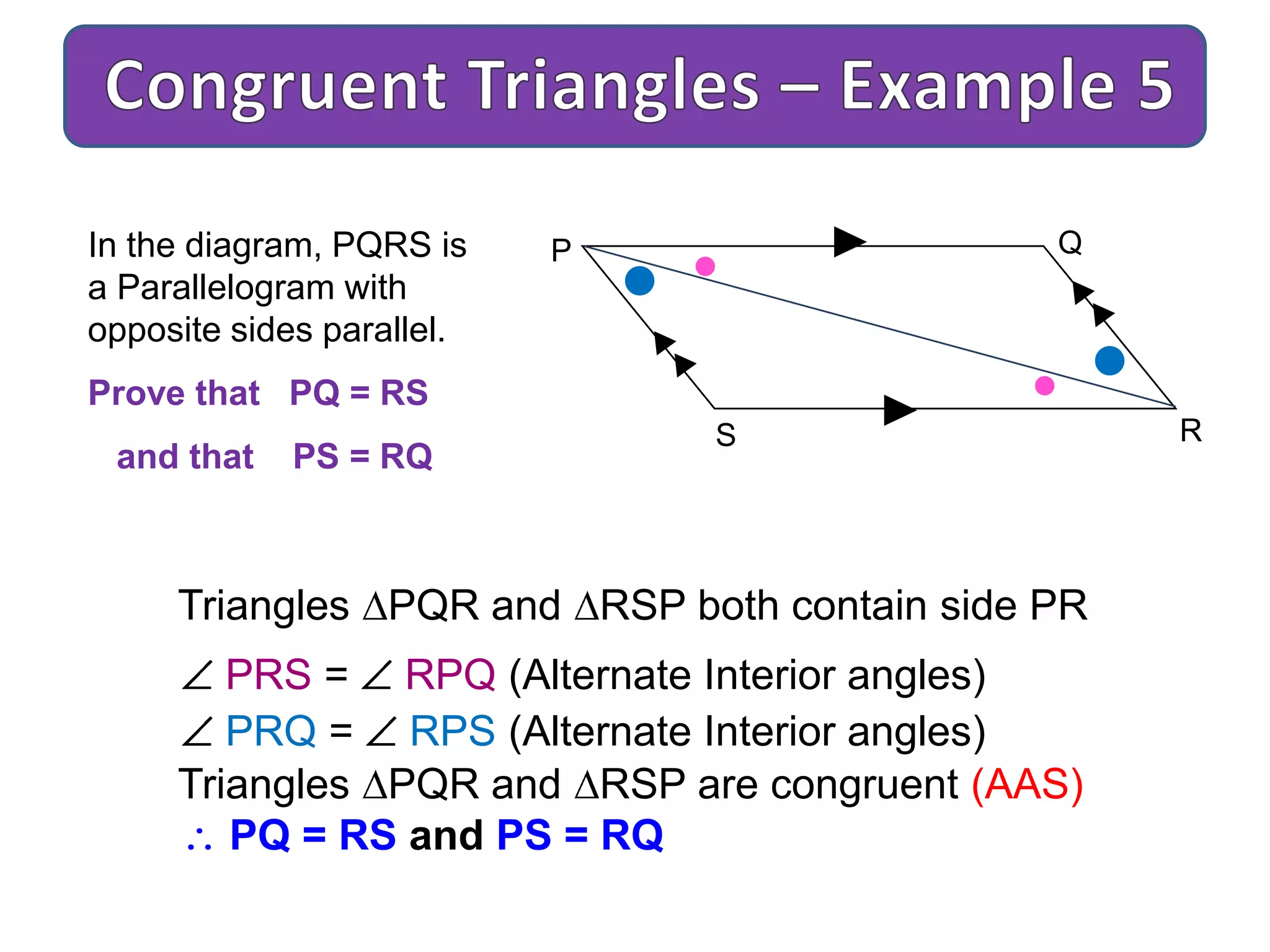
This document provides an overview of congruent triangles and the different rules that can be used to prove triangles are congruent. It defines congruent triangles as triangles that have the same size and shape. It then presents four main rules for proving triangles are congruent: 1) three sides are equal (SSS rule), 2) two sides and the included angle are equal (SAS rule), 3) two angles and a non-included side are equal (AAS rule), and 4) a right angle, hypotenuse, and one other side are equal (RHS rule). The document explains each rule and provides examples of how to apply them to identify matching elements and prove triangles congruent.

1. Image Source: http://resources3.news.com.au

2. Identical Twins have the exact same size and shape,
and we instantly recognise
that the two people are
are exactly the same.
When two items have the exact same size and shape,
we say that they are "Congruent".
This Presentation is all about "Congruent Triangles",
eg. Groups of Triangles which have the exact same
size and shape.

3. In the Real World Congruent Triangles are used in
Construction when we need to reinforce structures
so that they are strong and stable, and do not
bend or buckle in strong winds or when under load.

4. 7cm
9cm
Identical Triangles have all three Sides, and
all three Angles exactly the same sizes.
5cm
60o
85o 35o
5cm
9cm
60o
7cm
85o 35o
If we gave several people three sticks: 5cm, 7cm and 9cm long,
they would each only be able to make the exact same Triangle.

5. 7cm
9cm
Congruent Triangles do not have to be in the
same orientation or position. They only have
to be identical in size and shape.
5cm
60o
85o 35o
5cm9cm
60o
7cm
85o35o
The Green Triangle on the right, is an upside down version of
the Pink Triangle. They are both the same size and shape.

6. Identical Twins have over 1000 body parts which
are exactly the same.
HOWEVER, we only have to
check a few key items to tell
that they are "Congruent".
For "Congruent Triangles”, it turns out that we do
not actually have to check that all three Angles
and all three sides to prove they are Identical.
There are “Shortcut” Rules which we can use.

7. 7cm
9cm
5cm 5cm
9cm
7cm
Any Triangle with sides of 5cm, 7cm and 9cm long, can only be
one specific shape. In that shape the angles will be specific values.
Two triangles are congruent if:
All three Sides of the triangles are equal in length.

8. Triangles can have markings on their sides to indicate that pairs
of sides are the exact same length. The “SSS” rule can be applied.
Two triangles are congruent if:
All three Sides of the triangles are equal in length.

9. Triangles are labelled with Letters and special symbols used.
A B
C
D E
F
ABC DEF (by SSS Rule)
AB = DE and BC = EF and AC = DF

10. We need to be careful with labelling when orientation is different.
A B
C
D
E
F
ABC = DEF (by SSS Rule)
AB = DE and BC = EF and AC = DF
~

11. 7cm
5cm 5cm
7cm
If we label the Sides as “S”, and the Angle as “A”; then the pattern
as we trace around the Triangle is “Side Angle Side” or “SAS”.
Two triangles are congruent if:
Two matching sides have equal lengths, and
the angle in between these two sides is the same.
65o 65o

12. 5cm 5cm
If we label the Side as “S”, and the Angles as “A”; then the pattern
as we trace around the Triangle is “Angle Angle Side” or “AAS”.
Two triangles are congruent if:
Two matching angles are equal, and one matching
side is the same length in both triangles.
65o 65o40o 40o

13. 7cm 7cm
There was an old rule called “ASA” Angle Side Angle, but this is
now part of the “AAS” Rule. (Two Angles and One Side).
Two triangles are congruent if:
The order of the AAS Rule is not important, as
long as two angles are equal & one side the same.
65o 65o40o 40o

14. 8mm 8mm
This Rule works because of Pythagoras for 90 Degree Triangles
means that the missing side lengths are equal, so really “SSS”.
Two Right Angled Triangles are congruent if:
The Hypotenuse and one matching side are equal
in length. They also have a 90 degree angle equal.
10mm 10mm

15. Two sides and the included angle equal. (SAS)
Two angles and any matching side equal . (AAS)
Right angle, Hypotenuse and a Side (RHS)
Three sides equal. (SSS)

16. A
B
C
10cm
3 cm9 cm
X
Z
Y
10cm
3 cm9 cm
AB = XZ (Corresponding Equal Sides)
BC = ZY (Corresponding Equal Sides)
AC = XY (Corresponding Equal Sides)
ABC XYZ (by SSS Rule)
By identifying matching items, prove the Triangles are Congruent

17. A
B
C
9
AB = PQ (Corresponding Equal Sides)
B = Q (Corresponding Equal Angles)
BC = QR (Corresponding Equal Sides)
ABC PQR (by SAS Rule)
By identifying matching items, prove the Triangles are Congruent
5
85o
P
Q
R
9
5
85o

18. A
B
C
12mm
65o
20o
P
Q
R
12mm
65o
20o
A = P (Corresponding Equal Angles)
C = R (Corresponding Equal Angles)
AC = PR (Corresponding Equal Sides)
ABC PQR (by AAS Rule)
By identifying matching items, prove the Triangles are Congruent

19. A B
CD
M
AB is parallel to DC and
M is the midpoint of DB.
Show that the segment
AM = CM by proving
Congruent Triangles
ABM = CDM (Alternate Interior angles)
BAM = DCM (Alternate Interior angles)
Triangles ABM CDM are congruent ( by AAS)
AM = CM
The order of the lettering is important
when naming congruent triangles.
It would be wrong in this example to say that
triangles ABM and DCM are congruent.

20. P Q
RS
In the diagram, PQRS is
a Parallelogram with
opposite sides parallel.
Prove that PQ = RS
and that PS = RQ
PRS = RPQ (Alternate Interior angles)
PRQ = RPS (Alternate Interior angles)
Triangles PQR and RSP are congruent (AAS)
PQ = RS and PS = RQ
Triangles PQR and RSP both contain side PR

21. http://passyworldofmathematics.com/
All slides are exclusive Copyright of Passy’s World of Mathematics
Visit our site for Free Mathematics PowerPoints