The document provides an overview of fuzzy logic concepts including types of fuzzy systems, membership functions, fuzzy inference, fuzzification and defuzzification methods. It discusses knowledge-based and rule-based fuzzy systems, types of membership functions like triangular, trapezoidal and Gaussian. Examples of fuzzy logic applications in autonomous driving cars and methods for defuzzification like weighted average, centroid, max-membership and centre of sums are also summarized.


![4 of 38
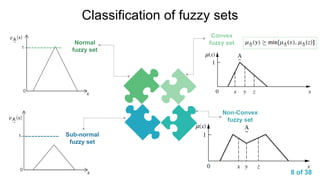
Human
knowledge-based
Rule-based
Fuzzy
IF AND
THEN
distance
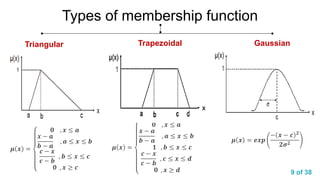
speed
acceleration
small
speed is declining
maintain
IF distance perfect AND
speed is declining
THEN increase acceleration
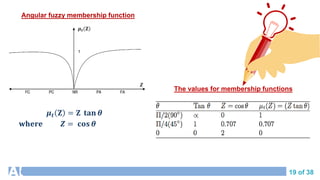
speed [m/s]](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-4-320.jpg)


![10 of 38
Autonomous driving car
distance
speed
acceleration
13 m
-2.5 m/s
?
Knowledge
Rule base
Distance to next car [ m ]
v.small small perfect big v.big
Speed
Change
[ 𝒎 𝟐
]
declining -ve small zero +ve small +ve big +ve big
constant -ve big -ve small zero +ve small +ve big
growing -ve big -ve big -ve small zero +ve small
speed [m/s]](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-10-320.jpg)
![11 of 38
speed [m/s]
Knowledge
Rule base
Distance to next car [ m ]
v.small small perfect big v.big
Speed
Change
[ 𝒎 𝟐
]
declining -ve small zero +ve small +ve big +ve big
constant -ve big -ve small zero +ve small +ve big
growing -ve big -ve big -ve small zero +ve small
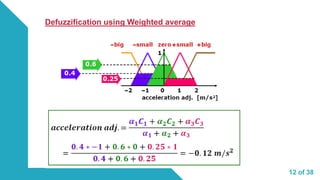
0.4 0.25
0.4
0.6
0.6
0.75
0.75
0.25
0.25
0.4
0.25
0.6
Rule 1: IF distance is small AND speed is declining
THEN acceleration zero
Rule 2: IF distance is small AND speed is constant
THEN acceleration negative small
Rule 3: IF distance is perfect AND speed is declining
THEN acceleration positive small
Rule 4: IF distance is perfect AND speed is constant
THEN acceleration zero
max
Take
min](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-11-320.jpg)





![24 of 38
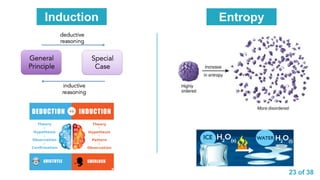
Inductive Reasoning 7
The induction is performed by the entropy
minimization principle, which clusters most
optimally the parameters corresponding to
the output classes [De Luca and Termini,
1972].
Particular General
useful for complex static systems
not useful for dynamic systems
1- subdivide our data set into membership functions
2- determine a threshold line with an entropy
minimization
3- start the segmentation process by moving an
imaginary threshold value x between x1 and x2
4-calculate entropy for each value of x.](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-24-320.jpg)

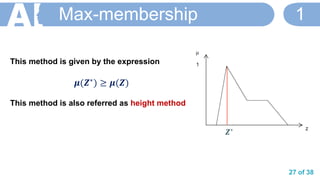

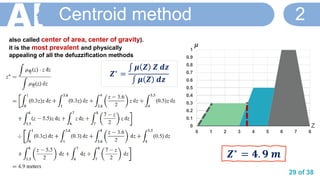
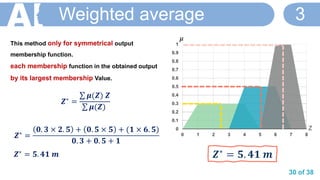
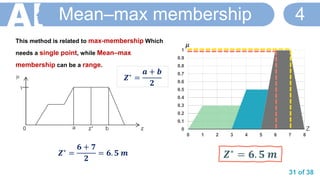
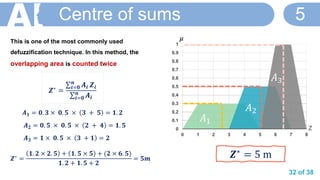
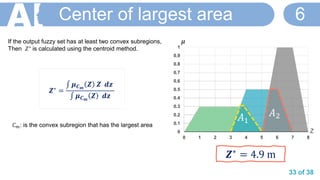
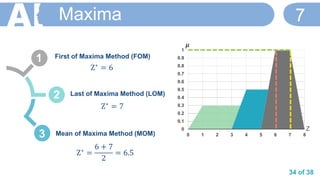
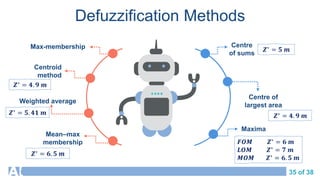
![36 of 38
References
[1] L.-X. Wang, A Course in Fuzzy Systems and Control. Prentice Hall PTR, 1997.
[2] S. N. Sivanandam, S. Sumathi, and S. N. Deepa, Introduction to Fuzzy Logic
using MATLAB. Springer, 2006.
[3] T. J. Ross, Fuzzy Logic with Engineering Applications, 2nd ed. Wiley, 2004.
[4] Essam Nabil, “Autonomous driving car,” March,2019, pp. 1–13.[presentation].](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-36-320.jpg)
![37 of 38
Slide 1 : [1] man thinking [2] working man
Slide 6 : [2] subway
Slide 7 : [1] sensor [2] system to be controlled
Slide 10 : [1] car
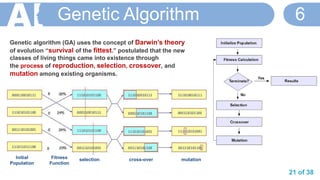
Slide 21 : [1] block diagram of genetic algorithm [2] Steps in Genetic Algorithms
Slide 23 : [1] deductive & inductive reasoning [2] entropy [3] ice and water
Sources of images](https://image.slidesharecdn.com/lect3-fuzzificationanddefuzzification-191204191413/85/fuzzy-fuzzification-and-defuzzification-37-320.jpg)
