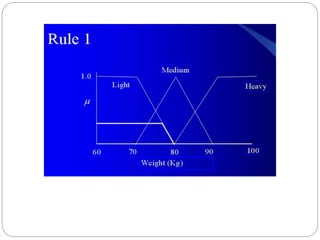
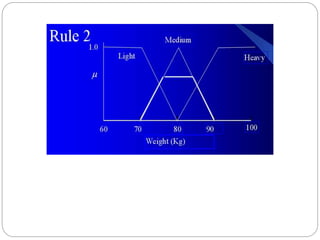
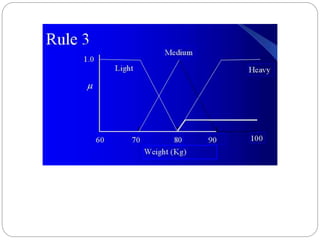
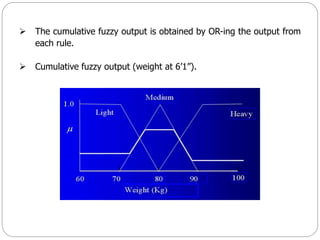
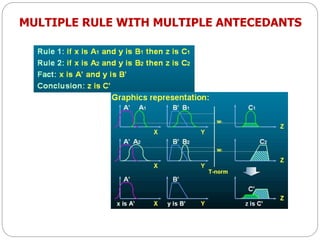
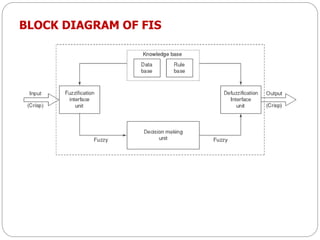
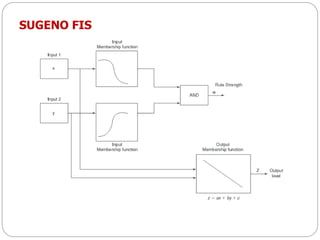
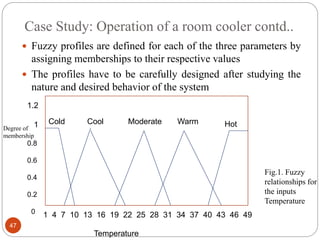
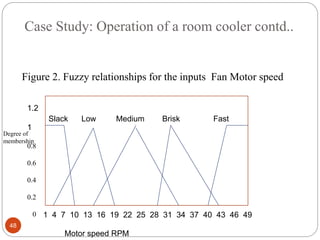
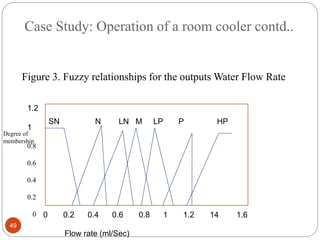
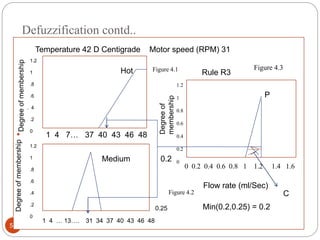
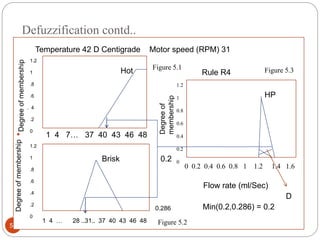
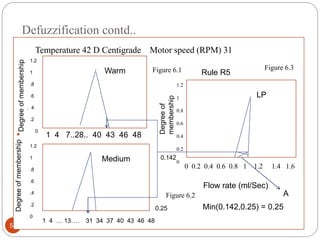
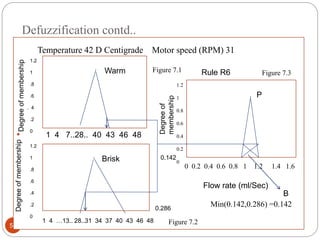
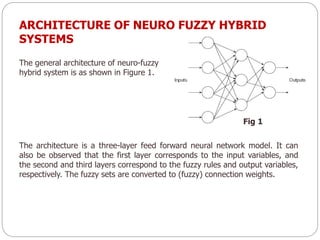
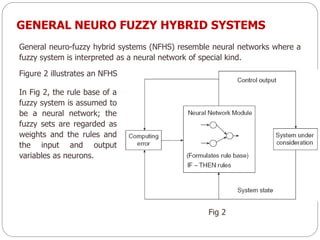
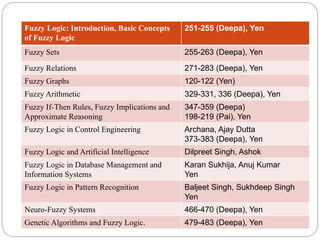
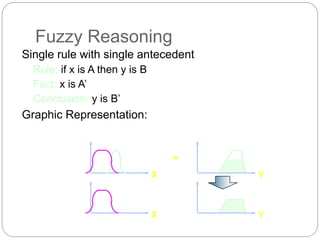
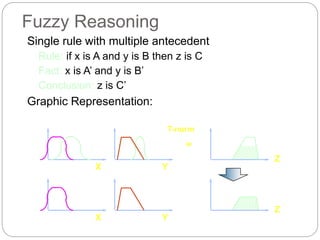
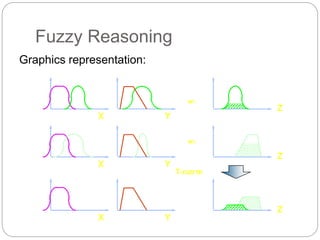
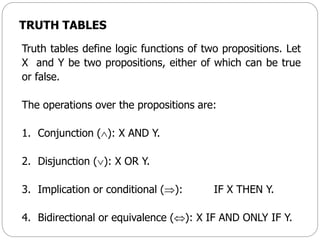
The document discusses fuzzy rule-based systems and fuzzy reasoning. It defines fuzzy if-then rules which have antecedents and consequents that are fuzzy sets rather than binary variables. Fuzzy reasoning can involve single or multiple rules with single or multiple antecedents. Graphical representations are used to illustrate the fuzzy reasoning process. The types of fuzzy inference systems including Mamdani and Sugeno systems are described along with their components and working. Applications of fuzzy logic in various domains are also mentioned.

1. FUZZY RULE BASE AND
APPROXIMATE
REASONING

2. Fuzzy If-Then Rules
 General format:
If x is A then y is B
 Examples:
 If pressure is high, then volume is small.
 If the road is slippery, then driving is dangerous.
 If a tomato is red, then it is ripe.
 If the speed is high, then apply the brake a little.

3. Fuzzy Reasoning
Single rule with single antecedent
Rule: if x is A then y is B
Fact: x is A’
Conclusion: y is B’
Graphic Representation:
A
X
w
A’ B
Y
x is A’
B’
Y
A’
X
y is B’

4. Fuzzy Reasoning
Single rule with multiple antecedent
Rule: if x is A and y is B then z is C
Fact: x is A’ and y is B’
Conclusion: z is C’
Graphic Representation:
A B T-norm
X Y
w
A’ B’ C2
Z
C’
Z
X Y
A’ B’
x is A’ y is B’ z is C’

5. Fuzzy Reasoning
Multiple rules with multiple antecedent
Rule 1: if x is A1 and y is B1 then z is C1
Rule 2: if x is A2 and y is B2 then z is C2
Fact: x is A’ and y is B’
Conclusion: z is C’
Graphic Representation: (next slide)

6. Fuzzy Reasoning
Graphics representation:
A1 B1
A2 B2
T-norm
X
X
Y
Y
w1
w2
A’
A’ B’
B’ C1
C2
Z
Z
C’
Z
X Y
A’ B’
x is A’ y is B’ z is C’

7. The degree of an element in a fuzzy set
corresponds to the truth value of a
proposition in fuzzy logic systems.
FUZZY RULES AND REASONING

8. LINGUISTIC VARIABLES
 A linguistic variable is a fuzzy variable.
• The linguistic variable speed ranges between 0 and
300 km/h and includes the fuzzy sets slow, very
slow, fast, …
• Fuzzy sets define the linguistic values.
 Hedges are qualifiers of a linguistic variable.
• All purpose: very, quite, extremely
• Probability: likely, unlikely
• Quantifiers: most, several, few
• Possibilities: almost impossible, quite possible

9. TRUTH TABLES
Truth tables define logic functions of two propositions. Let
X and Y be two propositions, either of which can be true
or false.
The operations over the propositions are:
1. Conjunction (): X AND Y.
2. Disjunction (): X OR Y.
3. Implication or conditional (): IF X THEN Y.
4. Bidirectional or equivalence (): X IF AND ONLY IF Y.

10. FUZZY RULES
A fuzzy rule is defined as the conditional statement of the
form
If x is A
THEN y is B
where x and y are linguistic variables and A and B are
linguistic values determined by fuzzy sets on the universes
of discourse X and Y.
IF height is tall THEN weight is heavy.

11.  The decision-making process is based on rules with sentence
conjunctives AND, OR and ALSO.
 Each rule corresponds to a fuzzy relation.
 Rules belong to a rule base.
 Example: If (Distance x to second car is SMALL) OR (Distance y
to obstacle is CLOSE) AND (speed v is HIGH) THEN (perform
LARGE correction to steering angle ) ALSO (make MEDIUM
reduction in speed v).
 Three antecedents (or premises) in this example give rise to two
outputs (consequences).

12. FUZZY RULE FORMATION
IF height is tall
THEN weight is heavy.
Here the fuzzy classes height and weight have a
given range (i.e., the universe of discourse).
range (height) = [140, 220]
range (weight) = [50, 250]

13. FORMATION OF FUZZY RULES
Three general forms are adopted for forming fuzzy rules.
They are:
 Assignment statements,
 Conditional statements,
 Unconditional statements.

14. Assignment Statements
Conditional Statements
Unconditional Statements

15. DECOMPOSITION OF FUZZY RULES
A compound rule is a collection of several simple
rules combined together.
 Multiple conjunctive antecedent,
 Multiple disjunctive antecedent,
 Conditional statements (with ELSE and
UNLESS).

16. DECOMPOSITION OF FUZZY RULES
Multiple Conjunctive
Antecedants
Conditional Statements ( With Else and Unless)
Multiple disjunctive
antecedent

17. AGGREGATION OF FUZZY RULES
Aggregation of rules is the process of obtaining the
overall consequents from the individual
consequents provided by each rule.
 Conjunctive system of rules.
 Disjunctive system of rules.

18. AGGREGATION OF FUZZY RULES
Conjunctive system of rules

19. Disjunctive system of rules

20. FUZZY RULE - EXAMPLE
Rule 1: If height is short then weight is light.
Rule 2: If height is medium then weight is medium.
Rule 3: If height is tall then weight is heavy.

21. Problem: Given
(a) membership functions for short, medium-
height, tall, light, medium-weight and heavy;
(b) The three fuzzy rules;
(c) the fact that John’s height is 6’1”
estimate John’s weight.

22. Solution:
(1) From John’s height we know that
John is short (degree 0.3)
John is of medium height (degree 0.6)
John is tall (degree 0.2)
(2) Each rule produces a fuzzy set as output by
truncating the consequent membership
function at the value of the antecedent
membership.

26.  The cumulative fuzzy output is obtained by OR-ing the output from
each rule.
 Cumulative fuzzy output (weight at 6’1”).

27. 1. De-fuzzify to obtain a numerical estimate of
the output.
2. Choose the middle of the range where the truth
value is maximum.
3. John’s weight = 80 Kg.
Two methods to de-fuzzification (yen 143-145)
1. Mean of Maximum (MoM)
2. Centre of Area (CoA)

28. FUZZY REASONING
There exist four modes of fuzzy approximate reasoning,
which include:
1. Categorical reasoning,
2. Qualitative reasoning,
3. Syllogistic reasoning,
4. Dispositional reasoning.

29. REASONING WITH FUZZY RULES
 In classical systems, rules with true antecedents fire.
(Like if a is true only then b is implemented)
IF height is tall THEN weight is heavy.
 In fuzzy systems, truth (i.e., membership in some class) is relative,
so all rules fire (to some extent).

30. SINGLE RULE WITH SINGLE ANTECEDANT

31. MULTIPLE ANTECEDANTS

32. MULTIPLE ANTECEDANTS
IF x is A AND y is B THEN z is C
IF x is A OR y is B THEN z is C
Use unification (OR) or intersection (AND) operations to
calculate a membership value for the whole antecedent.

33. MULTIPLE RULE WITH MULTIPLE ANTECEDANTS

34. MULTIPLE CONSEQUENTS
IF x is A THEN y is B AND z is C
Each consequent is affected equally by the membership in
the antecedent class(es).
E.g., IF x is tall THEN x is heavy AND x has large feet.

35. FUZZY INFERENCE SYSTEMS (FIS)
 Fuzzy rule based systems, fuzzy models, and fuzzy
expert systems are also known as fuzzy inference
systems.
 The key unit of a fuzzy logic system is FIS.
 The primary work of this system is decision-making.
 FIS uses “IF...THEN” rules along with connectors “OR”
or “AND” for making necessary decision rules.
 The input to FIS may be fuzzy or crisp, but the output
from FIS is always a fuzzy set.
 When FIS is used as a controller, it is necessary to have
crisp output.
 Hence, there should be a defuzzification unit for
converting fuzzy variables into crisp variables along FIS.

36. BLOCK DIAGRAM OF FIS

37. TYPES OF FIS
There are two types of Fuzzy Inference Systems:
 Mamdani FIS(1975)
 Sugeno FIS(1985)

38. MAMDANI FUZZY INFERENCE SYSTEMS (FIS)
 Fuzzify input variables:
• Determine membership values.
 Evaluate rules:
• Based on membership values of (composite)
antecedents.
 Aggregate rule outputs:
• Unify all membership values for the output from
all rules.
 Defuzzify the output:
• COG: Center of gravity (approx. by summation).

39. SUGENO FUZZY INFERENCE SYSTEMS (FIS)
The main steps of the fuzzy inference process namely,
1. fuzzifying the inputs and
2. applying the fuzzy operator are exactly the same as in
MAMDANI FIS.
The main difference between Mamdani’s and Sugeno’s
methods is that Sugeno output membership functions are
either linear or constant.

40. SUGENO FIS

41. SUMMARY
 Advantages of fuzzy logic
• Allows the use of vague linguistic terms in the rules.
 Disadvantages of fuzzy logic
• Difficult to estimate membership function
• There are many ways of interpreting fuzzy rules,
combining the outputs of several fuzzy rules and de-
fuzzifying the output.

42. Fuzzy Inference Processing
42
• There are three models for Fuzzy processing based on the
expressions of consequent parts in fuzzy rules
Suppose xi are inputs and y is the consequents in fuzzy
rules
1. Mamdani Model: y = A
where A is a fuzzy number to reflect fuzziness
• Though it can be used in all types of systems, the model
is more suitable for knowledge processing systems than
control systems

43. Fuzzy Inference Processing contd..
43
2. TSK (Takagi-Sugano-Kang) model:
y = a0 + Ʃ ai xi where ai are constants
The output is the weighted linear combination of
input variables (it can be expanded to nonlinear
combination of input variables)
Used in fuzzy control applications
3. Simplified fuzzy model: y = c
where c is a constant
Thus consequents are expressed by constant values

44. Applications of Fuzzy Logic
44
 Fuzzy logic has been used in many applications including
- Domestic appliances like washing machines and cameras
-Sophisticated applications such as turbine control, data
classifiers etc.
- Intelligent systems that use fuzzy logic employ
techniques for learning and adaptation to the environment

45. Case Study: Controlling the speed of a motor in a room cooler
45
• Through this case study we can understand fuzzy
logic, defining fuzzy rules and fuzzy inference and
control mechanisms
• Mamdani style of inference processing is used
• Problem: A room cooler has a fan encased in a box
with wool or hay. The wool is continuously
moistened by water that flows through a pump
connected to a motor. The rate of flow of water is to
be determined; it is a function of room temperature
and the speed of motor
• The speed of the motor is based on two parameters:
temperature and humidity; humidity is increased to reduce
temperature

46. Case Study: Operation of a room cooler contd..
46
• Two input variables –room temperature and cooler
fan speed control the output variable – flow rate of
the water. The fuzzy regions using fuzzy terms for
input-output are defined as follows
Variable name Fuzzy terms
Temperature Cold, Cool, Moderate, Warm and Hot
Fan speed Slack, Low, Medium, Brisk, fast
((rotations per minute)
Flow rate of water Strong Negative (SN), Negative (N),
Low-Negative (LN), Medium (M), Low-Positive
(LP), Positive (P), and High-Positive (HP)

47. Case Study: Operation of a room cooler contd..
47
 Fuzzy profiles are defined for each of the three parameters by
assigning memberships to their respective values
 The profiles have to be carefully designed after studying the
nature and desired behavior of the system
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49
Temperature
Degree of
membership
Cold Cool Moderate Warm
Fig.1. Fuzzy
relationships for
the inputs
Temperature
1.2
1
0.8
0.6
0.4
0.2
0
Hot

48. Case Study: Operation of a room cooler contd..
48
Figure 2. Fuzzy relationships for the inputs Fan Motor speed
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49
Motor speed RPM
Degree of
membership
Slack Low Medium Brisk Fast
1.2
1
0.8
0.6
0.4
0.2
0
Slack Low Medium Brisk Fast

49. Case Study: Operation of a room cooler contd..
49
Figure 3. Fuzzy relationships for the outputs Water Flow Rate
0 0.2 0.4 0.6 0.8 1 1.2 14 1.6
Flow rate (ml/Sec)
Degree of
membership
SN N LN M LP P HP
1.2
1
0.8
0.6
0.4
0.2
0

50. Fuzzy Rules for fuzzy room cooler
50
 The fuzzy rules form the triggers of the fuzzy engine
 After a study of the system, the rules could be written as
follows
R1: If temperature is HOT and fan motor speed is
SLACK then the flow-rate is HIGH-POSITIVE
R2: If temperature is HOT and fan motor speed is LOW
then the flow-rate is HIGH-POSITIVE
R3: If temperature is HOT and fan motor speed is
MEDIUM then the flow-rate is POSITIVE
R4: If temperature is HOT and fan motor speed is
BRISK then the flow-rate is HIGH-POSITIVE

51. Fuzzy Rules for fuzzy room cooler contd..
51
 R5: If temperature is WARM and fan motor speed is
MEDIUM then the flow-rate is LOW-POSITIVE
 R6: If temperature is WARM and fan motor speed is
BRISK then the flow-rate is POSITIVE
 R7: If temperature is COOL and fan motor speed is
LOW then the flow-rate is NEGATIVE
 R8: If temperature is MODERATE and fan motor
speed is LOW then the flow-rate is MEDIUM

52. Fuzzification
52
 The fuzzifier that performs the mapping of the
membership values of the input parameters temperature
and fan speed to the respective fuzzy regions is known as
fuzzification. This is the most important step in fuzzy
systems
 Suppose that at some time t, the temperature is 42 degrees
and fan speed is 31 rpm. The corresponding membership
values and the fuzzy regions are shown in Table 2

53. Example of fuzzification
53
 From Figure 1., the temperature 42 degrees
correspond to two membership values 0.142 and 0.2
that belong to WARM and HOT fuzzy regions
respectively
 Similarly From Figure 2., the fan speed 31 rpm
corresponds to two membership values 0.25 and
0.286 that belong to MEDIUM and BRISK fuzzy
regions respectively Table 2
Parameters Fuzzy Regions Memberships
Temperature Warm, hot 0.142, 0.2
Fan Speed medium, brisk 0.25, 0.286

54. Example of fuzzification contd..
54
 From Table 2, there are four combinations possible
 If temperature is WARM and fan speed is MEDIUM
 If temperature is WARM and fan speed is BRISK
 If temperature is HOT and fan speed is MEDIUM
 If temperature is HOT and fan speed is BRISK
 Comparing the above combinations with the left side
of fuzzy rules R5, R6, R3, and R4 respectively, the
flow-rate should be LOW-POSITIVE, POSITIVE,
POSITIVE and HIGH-POSITIVE
 The conflict should be resolved and the fuzzy region is to be
given as a value for the parameter water flow-rate

55. Defuzzification
55
• The fuzzy outputs LOW-POSITIVE, POSITIVE, and HIGH-
POSITIVE are to be converted to a single crisp value that is
provided to the fuzzy cooler system; this process is called
defuzzification
• Several methods are used for defuzzification
• The most common methods are
1. The centre of gravity method and
2. The Composite Maxima method
The centroid, of a two-dimensional shape X is the intersection of all
straight lines that divide X into two parts of equal moment about the line
or the average of all points of X. (Moment is a quantitative measure of the
shape of a set of points.)
In both these methods the composite region formed by the
portions A, B, C, and D (corresponding to rules R3, R4, R5
and R6 respectively) on the output profile is to be computed

56. Defuzzification contd..
56
• ttttt 1 4 7… 37 40 43 46 48
DegreeofmembershipDegreeofmembership
Degreeof
membership
1 4 … 13…. 31 34 37 40 43 46 48
1.2
1
.8
.6
. 4
.2
0
1.2
1
.8
.6
.4
.2
0
Hot
Medium
Temperature 42 D Centigrade Motor speed (RPM) 31
0.25
1.2
1
0.8
0.6
0.4
0.2
0
Rule R3
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
P
0.2
Flow rate (ml/Sec)
Min(0.2,0.25) = 0.2
C
Figure 4.1
Figure 4.2
Figure 4.3

57. Defuzzification contd..
57
• ttttt 1 4 7… 37 40 43 46 48
DegreeofmembershipDegreeofmembership
Degreeof
membership
1 4 … 28 ..31.. 37 40 43 46 48
1.2
1
.8
.6
. 4
.2
0
1.2
1
.8
.6
.4
.2
0
Hot
Brisk
Temperature 42 D Centigrade Motor speed (RPM) 31
0.286
1.2
1
0.8
0.6
0.4
0.2
0
Rule R4
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
HP
0.2
Flow rate (ml/Sec)
Min(0.2,0.286) = 0.2
D
Figure 5.1
Figure 5.2
Figure 5.3

58. Defuzzification contd..
58
• ttttt 1 4 7..28.. 40 43 46 48
DegreeofmembershipDegreeofmembership
Degreeof
membership
1 4 … 13…. 31 34 37 40 43 46 48
1.2
1
.8
.6
. 4
.2
0
1.2
1
.8
.6
.4
.2
0
Warm
Medium
Temperature 42 D Centigrade Motor speed (RPM) 31
0.25
1.2
1
0.8
0.6
0.4
0.2
0
Rule R5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
LP
0.142
Flow rate (ml/Sec)
Min(0.142,0.25) = 0.25
A
Figure 6.1
Figure 6.2
Figure 6.3

59. Defuzzification contd..
59
• ttttt 1 4 7..28.. 40 43 46 48
DegreeofmembershipDegreeofmembership
Degreeof
membership
1 4 …13.. 28..31 34 37 40 43 46 48
1.2
1
.8
.6
. 4
.2
0
1.2
1
.8
.6
.4
.2
0
Warm
Brisk
Temperature 42 D Centigrade Motor speed (RPM) 31
0.286
1.2
1
0.8
0.6
0.4
0.2
0
Rule R6
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
P
0.142
Flow rate (ml/Sec)
Min(0.142,0.286) =0.142
B
Figure 7.1
Figure 7.2
Figure 7.3

60. Defuzzification contd..
60
Degreeof
membership
Temperature 42 D Centigrade Motor speed (RPM) 31
1.2
1
0.8
0.6
0.4
0.2
0
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
P
Flow rate (ml/Sec)
LP
HP
Centroid
A B is within C as it
is a subset of the
region C
D
Figure 8When parameters are connected by AND the
minimum of their memberships is taken
The area C is the region formed by the
application of rule R3 as shown in Figure 4.3
The area D is the region formed by the
application of rule R4 as shown in Figure 5.3
The area A is the region formed by the
application of rule R5 as shown in Figure 6.3
The area B is the region formed by the
application of rule R6 as shown in Figure 7.3
The composite region formed by the portions
A, B, C and D on the output profile is shown
in Figure 8.
The centre of gravity of this composite
region is the crisp output or the desired flow
rate value

61. Steps in Fuzzy logic based system
 Formulating fuzzy regions
 Fuzzy rules
 Embedding a Defuzzification procedure
In Defuzzification procedure, depending on the
application, either the centre of gravity or the
composite maxima is found to obtain the crisp output

62. HYBRID SOFT
COMPUTING
TECHNIQUES

63. Neural Network Systems
Neural networks are the simplified models of the human nervous
systems mimicking our ability to adapt to certain situations and to
learn from the past experiences.
Fuzzy Logic
Fuzzy logic or fuzzy systems deal with uncertainty or vagueness
existing in a system and formulating fuzzy rules to find a solution to
problems.
Genetic Algorithm
Genetic algorithms inspired by the natural evolution process are
adaptive search and optimization algorithms.
HYBRID SYSTEMS

64. The main aim of the concept of hybridization is to overcome the
weakness in one technique while applying it and bringing out the
strength of the other technique to find solution by combining them.
Neural networks are good at recognizing patterns but they are not
good at explaining how they reach their decisions.
On the contrary, fuzzy logic is good at explaining the decisions but
cannot automatically acquire the rules used for making the decisions.
Also, the tuning of membership functions becomes an important issue
in fuzzy modeling. Genetic algorithms offer a possibility to solve this
problem.
These limitations act as a central driving force for the creation of
hybrid soft computing systems where two or more techniques are
combined in a suitable manner that overcomes the limitations of
individual techniques.

65. The use of hybrid systems is growing rapidly with successful
applications in areas such as
 engineering design
 stock market analysis and prediction
 medical diagnosis
 process control
 credit card analysis and
 few other cognitive simulations.

66. VARIOUS HYBRID SYSTEMS
In this text book, the following three different hybrid systems are discussed:
 Neuro fuzzy hybrid system;
 neuron genetic hybrid system;
 fuzzy genetic hybrid systems.

67. NEURO FUZZY HYBRID SYSTEMS
Definition:
A neuro-fuzzy hybrid system (also called fuzzy neural hybrid) is a learning
mechanism that utilizes the training and learning algorithms from neural
networks to find parameters of a fuzzy system.
Advantages of neuro fuzzy hybrid systems:
 It can handle any kind of information (numeric, linguistic, logical, etc.).
 It can manage imprecise, partial, vague or imperfect information.
 It can resolve conflicts by collaboration and aggregation.
 It has self-learning, self-organizing and self-tuning capabilities.
 It doesn’t need prior knowledge of relationships of data.

68. ARCHITECTURE OF NEURO FUZZY HYBRID
SYSTEMS
Fig 1
The general architecture of neuro-fuzzy
hybrid system is as shown in Figure 1.
The architecture is a three-layer feed forward neural network model. It can
also be observed that the first layer corresponds to the input variables, and
the second and third layers correspond to the fuzzy rules and output variables,
respectively. The fuzzy sets are converted to (fuzzy) connection weights.

69. TYPES OF NEURO FUZZY HYBRID SYSTEMS
NFSs can be classified into the following two systems:
1. Cooperative NFSs.
2. General neuro-fuzzy hybrid systems.

70. CO-OPERATIVE NEURO FUZZY SYSTEMS
In this type of system, both artificial neural network (ANN) and fuzzy system
work independently from each other. The ANN attempts to learn the
parameters from the fuzzy system.

71. GENERAL NEURO FUZZY HYBRID SYSTEMS
General neuro-fuzzy hybrid systems (NFHS) resemble neural networks where a
fuzzy system is interpreted as a neural network of special kind.
Fig 2
Figure 2 illustrates an NFHS
In Fig 2, the rule base of a
fuzzy system is assumed to
be a neural network; the
fuzzy sets are regarded as
weights and the rules and
the input and output
variables as neurons.

72. GENETIC FUZZY HYBRID SYSTEMS
The hybridization of genetic algorithm and fuzzy logic can be performed in the
following two ways:
1. By the use of fuzzy logic based techniques for improving genetic algorithm
behavior and modeling GA components. This is called fuzzy genetic algorithms
(FGAs).
2. By the application of genetic algorithms in various optimization and search
problems involving fuzzy systems.

73. ADVANTAGES OF GENETIC FUZZY HYBRID
SYSTEMS
GAs allow us to represent different kinds of structures, such as weights,
features together with rule parameters, etc., allowing us to code multiple
models of knowledge representation. This provides a wide variety of
approaches where it is necessary to design specific genetic components for
evolving a specific representation.
Genetic algorithm efficiently optimizes the rules, membership functions, DB and
KB of fuzzy systems. The methodology adopted is simple and the fittest
individual is identified during the process.

74. Fuzzy Logic: Intelligence, Control, And
Information
By Yen
74

75. 75

76. 76

77. Fuzzy Logic: Introduction, Basic Concepts
of Fuzzy Logic
251-255 (Deepa), Yen
Fuzzy Sets 255-263 (Deepa), Yen
Fuzzy Relations 271-283 (Deepa), Yen
Fuzzy Graphs 120-122 (Yen)
Fuzzy Arithmetic 329-331, 336 (Deepa), Yen
Fuzzy If-Then Rules, Fuzzy Implications and
Approximate Reasoning
347-359 (Deepa)
198-219 (Pai), Yen
Fuzzy Logic in Control Engineering Archana, Ajay Dutta
373-383 (Deepa), Yen
Fuzzy Logic and Artificial Intelligence Dilpreet Singh, Ashok
Fuzzy Logic in Database Management and
Information Systems
Karan Sukhija, Anuj Kumar
Yen
Fuzzy Logic in Pattern Recognition Baljeet Singh, Sukhdeep Singh
Yen
Neuro-Fuzzy Systems 466-470 (Deepa), Yen
Genetic Algorithms and Fuzzy Logic. 479-483 (Deepa), Yen