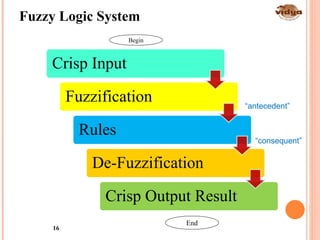
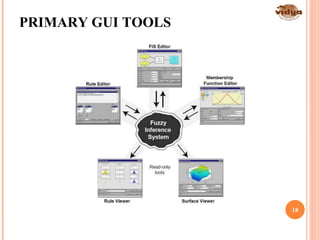
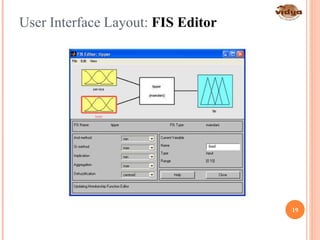
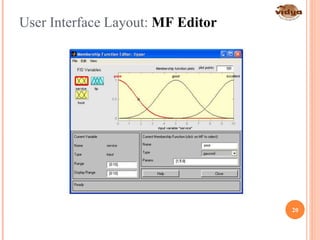
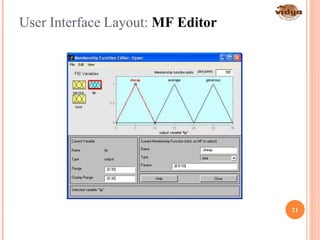
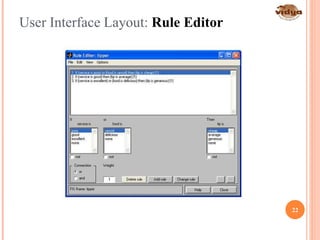
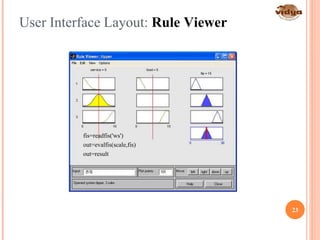
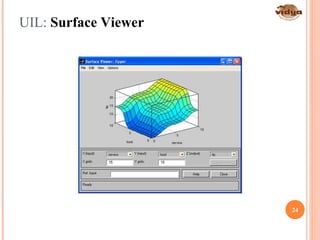
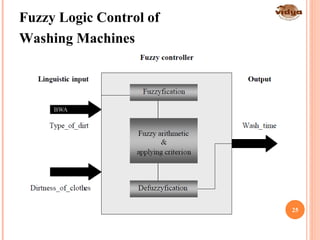
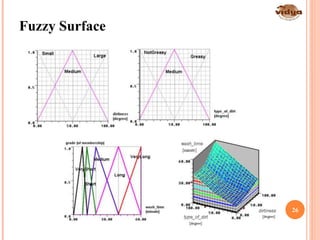
The document outlines the vision and mission of the Department of Electronics and Communication Engineering, emphasizing progress through knowledge in technology. It provides an introduction to fuzzy logic and its development by Professor Lotfi Zadeh, detailing its history, principles, and applications across various industries. Fuzzy logic is presented as a method for representing imprecision and improving the efficiency of control systems.

1. Dept. of Electronics and Communication Engg.
Vision: Progress through the growing knowledge of Electronics and Communication technology.
Mission: To emerge as a world class center of learning, research and development, integrating with the latest trends
in Electronics and Communication Engineering for the service of humanity.
15.01.2015
Prof. Dr. S. Swapna Kumar
Introduction to
FUZZY LOGIC

2. Professor Dr. Lotfali Asker Zadeh
Born: February 4, 1921 (age 93)
Baku, Soviet, Azerbaijan
Professional affiliation
Professor in the Graduate School, Computer Science Division
Department of Electrical Engineering and Computer Sciences
University of California
Berkeley, CA 94720 -1776
Director, Berkeley Initiative in Soft Computing (BISC)
zadeh@eecs.berkeley.edu
http://www.cs.berkeley.edu/~zadeh/
Tel.(office): (510) 642-4959
Fax (office): (510) 642-1712
Tel.(home): (510) 526-2569
Fax (home): (510) 526-2433
 1938: Alborz International High School, Tehran, Iran.
 1942: B.S. engineering degree, University of Tehran, Iran.
 1946 : M.S., Massachusetts Institute of Technology.
 1949: PhD – (Electrical Engineering}, Columbia University.
 Faculty member: Columbia University and the University of
California-Berkeley.
 1990: Retired from UC-Berkeley
 Director of UC Berkeley Initiative on Soft Computing.
2

3. Adversity
*Fuzzy Logic: Intelligence, Control, and Information - J. Yen and R. Langari, Prentice Hall 1999
1964: Lotfi A. Zadeh, UC Berkeley, introduced the
paper on fuzzy sets.
 Idea of grade of membership was born
 Sharp criticism from academic community
 Name!
 Theory’s emphasis on imprecision
 Waste of government funds!
3

4. History of Fuzzy Logic
*Fuzzy Logic: Intelligence, Control, and Information - J. Yen and R. Langari, Prentice Hall 1999
 1965: Zadeh introduced fuzzy set theory
1970s: research groups were form in JAPAN
1974: Mamdani, United Kingdom, developed the first fuzzy
logic controller
1977: Dubois applied fuzzy sets in a comprehensive study of
traffic conditions
1976-1987: Industrial application of fuzzy logic in Japan and
Europe
1987-Present: Fuzzy Boom 4

5. Precision is not ULTIMATE truth
5

6. Traditional logic
A rose is either RED or not RED.
6

7. Traditional (crisp) logic
What about this rose?
7

8. Precision & Significant in Real world
 Fuzzy logic relative importance of precision; when a rough
answer will do.
8

9. What/How……!!!!
FastestSlow FastSlowest
[ 0.1 – 0.25 ] [ 0.25 – 0.50 ] [ 0.50 – 0.75 ] [ 0.75 – 1.00 ]
 Very tall ~ 7f
 Tall ~ 6f
 Average ~ 5f
 Short ~ 4f
 Very short ~ 3f
9

10. 10
What is FUZZY LOGIC?
 Fuzzy logic:
 A way to represent variation or imprecision in logic
 A way to make use of natural language in logic
 Approximate reasoning
 Linguistic variables:
 Temp: {freezing, cool, warm, hot}
 Cloud Cover: {overcast, partly cloudy, sunny}
 Speed: {slow, fast}
 Problem-solving methodology
 Definite conclusion

11. Fuzzy Sets
NOTE: FUZZY SET IS NOT A “SET” but is a mapping
A x x x XA {( , ( ))| }
Universe or
universe of discourseFuzzy set
Membership
Function (MF)
A fuzzy set is totally characterized by a
membership function (MF).
Integer
11

12. Membership function
 A membership function (MF) is a curve that maps input space
to a membership value between 0 and 1.



























cxif
cxbif
bc
xc
bxaif
ab
ax
axif
xA
0
0
)(
a b c x
µA(x)
1
0
12

13. Membership Functions (MFs)
13

14. 14
 Is water colorless?
 CRISP Yes = 1, No = 0
 Is I am honest?
 Extremely honest = 1
 Very honest = 0.80
 Honest at times = 0.4
 Extremely dishonest = 0
Crisp Vs.. Fuzzy

15. Membership Functions
 Fuzzy logic Connectives:
 Fuzzy Disjunction, 
 Fuzzy Conjunction, 
1550 70 90 1103010
Temp. (F°)
Freezing Cool Warm Hot
0
1
0.7
0.3
How cool is 36 F° ?
µA(x)
Michio SugenoEbrahim Mamdani

16. Fuzzy Logic System
16
Crisp Input
Fuzzification
Rules
De-Fuzzification
Crisp Output Result
“antecedent”
“consequent”
Begin
End

17. FUZZY LOGIC USING MATLAB
17

18. PRIMARY GUI TOOLS
18

19. User Interface Layout: FIS Editor
19

20. User Interface Layout: MF Editor
20

21. User Interface Layout: MF Editor
21

22. User Interface Layout: Rule Editor
22

23. User Interface Layout: Rule Viewer
23
fis=readfis('ws')
out=evalfis(scale,fis)
out=result

24. UIL: Surface Viewer
24

25. Fuzzy Logic Control of
Washing Machines
25
BWA

26. Fuzzy Surface
26

27. 27
Drawbacks to Fuzzy logic
 Requires tuning of membership functions
 Fuzzy Logic control may not scale well to large or
complex problems
 Deals with imprecision, and vagueness, but not
uncertainty

28. Fuzzy Logic Applications
 Aerospace
 Automotive
 Business
 Chemical Industry
 Defense
 Electronics
 Financial
 Industrial
 Manufacturing
 Marine
 Medical
 Signal Processing
 Telecommunications
 Transportation
28

29. Summary
 Fuzzy logic provides an alternative way to represent
linguistic and subjective attributes of the real world in
computing.
 It is able to be applied to control systems and other
applications in order to improve the efficiency and
simplicity of the design process.
29

30. 30
References
 L. Zadah, “Fuzzy sets as a basis of possibility” Fuzzy
Sets Systems, Vol. 1, pp3-28, 1978.
 T. J. Ross, “Fuzzy Logic with Engineering
Applications”, McGraw-Hill, 1995.
 K. M. Passino, S. Yurkovich, "Fuzzy Control" Addison
Wesley, 1998.
 Google…..

31. zadeh@eecs.berkeley.edu
Questions
31

32. Thank You
drsswapnakumar@gmail.com