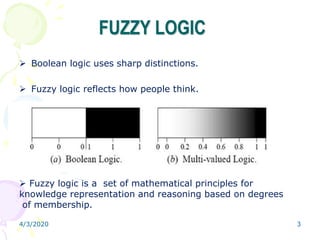
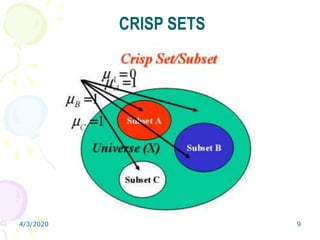
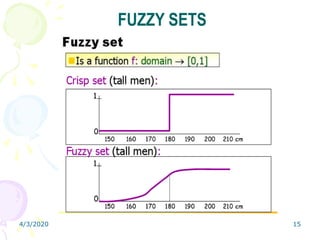
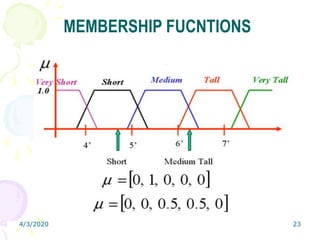
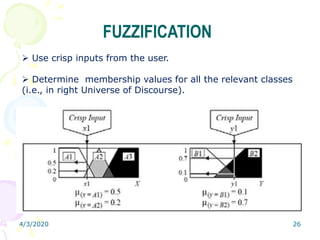
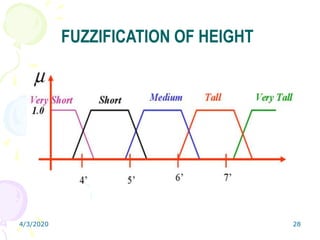
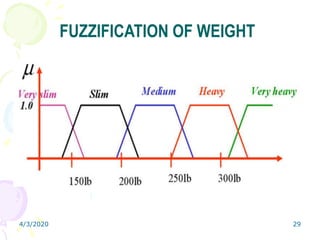
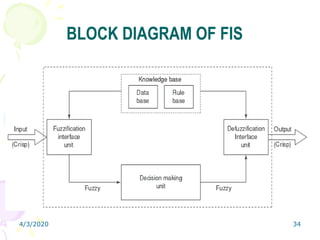
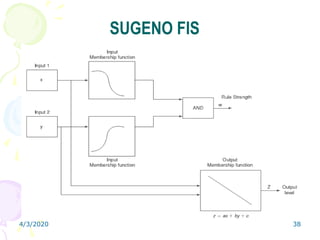
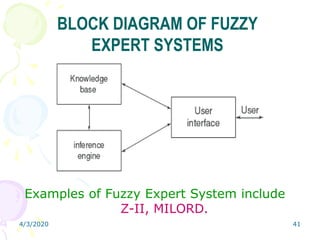
Fuzzy logic is a form of multivalued logic that allows intermediate values between conventional evaluations like true/false, yes/no, or high/low. It provides a mathematical framework for representing uncertainty and imprecision in measurement and human cognitive processes. Fuzzy logic systems use fuzzy membership functions and fuzzy "IF-THEN" rules to map inputs to outputs. They include fuzzification of inputs, an inference system to evaluate rules, aggregation of outputs, and defuzzification to produce a crisp output. Common applications include controllers that can handle complex or imprecise inputs better than conventional digital controllers.

1. 4/3/2020 1
INTRODUCTION TO FUZZY
LOGIC CONTROL
BY
Mr.A.Arulkumar,
Assistant Professor
Dept. of Mechatronics Engg
Kamaraj College of Engg &Technology
Email :
arulkumarmtr@kamarajengg.edu.in

2. FUZZY LOGIC
 Fuzzy logic is the logic underlying approximate, rather than
exact, modes of reasoning.
 It is an extension of multivalued logic: Everything, including
truth, is a matter of degree.
 It contains as special cases not only the classical two-value
logic and multivalue logic systems, but also probabilistic
logic.
 A proposition p has a truth value
• 0 or 1 in two-value system,
• element of a set T in multivalue system,
• Range over the fuzzy subsets of T in fuzzy logic.
4/3/2020 2

3. FUZZY LOGIC
 Boolean logic uses sharp distinctions.
 Fuzzy logic reflects how people think.
• Fuzzy logic is a set of mathematical principles for
4/3/2020 3
 Fuzzy logic is a set of mathematical principles for
knowledge representation and reasoning based on degrees
of membership.

4. 4/3/2020 4
TYPES AND MODELING OF
UNCERTAINTY

5. 4/3/2020 5
FUZZY vs PROBABILITY
 Fuzzy ≠ Probability
 Probability deals with uncertainty an
likelihood
 Fuzzy logic deals with ambiguity an
vagueness

6. 4/3/2020 6
FUZZY vs PROBABILITY

7. 4/3/2020 7
NEED OF FUZZY LOGIC
 Based on intuition and judgment.
 No need for a mathematical model.
 Provides a smooth transition between
members and nonmembers.
 Relatively simple, fast and adaptive.
 Less sensitive to system fluctuations.
 Can implement design objectives, difficult
to express mathematically, in linguistic or
descriptive rules.

8. 4/3/2020 8
CLASSICAL SETS (CRISP SETS)
Conventional or crisp sets are
Binary. An element either belongs to
the set or does not.
{True, False}
{1, 0}

9. 4/3/2020 9
CRISP SETS

10. 4/3/2020 10
OPERATIONS ON CRISP SETS
 UNION:
 INTERSECTION:
 COMPLEMENT:
 DIFFERENCE:

11. 4/3/2020 11
PROPERTIES OF CRISP SETS
The various properties of crisp sets are as follows:

12. 4/3/2020 12
PROPERTIES OF CRISP SETS

13. 4/3/2020 13
FUZZY SETS

14. 4/3/2020 14
FUZZY SETS

15. 4/3/2020 15
FUZZY SETS

16. 4/3/2020 16
OPERATIONS ON FUZZY SETS

17. 4/3/2020 17
PROPERTIES OF FUZZY SETS

18. 4/3/2020 18
PROPERTIES OF FUZZY SETS

19. 4/3/2020 19
PROPERTIES OF FUZZY SETS

20. 4/3/2020 20
LINGUISTIC VARIABLE

21. 4/3/2020 21
LINGUISTIC VARIABLE
 Let x be a linguistic variable with the label “speed”.
 Terms of x, which are fuzzy sets, could be “positive low”,
“negative high” from the term set T:
T = {PostiveHigh, PositiveLow, NegativeLow,
NegativeHigh, Zero}
 Each term is a fuzzy variable defined on the base variable
which might be the scale of all relevant velocities.

22. 4/3/2020 22
MEMBERSHIP FUCNTIONS

23. 4/3/2020 23
MEMBERSHIP FUCNTIONS

24. 4/3/2020 24
FEATURES OF MEMBERSHIP
FUNCTIONS
 CORE:
 SUPPORT:
 BOUNDARY:

25. 4/3/2020 25
FUZZIFICATION

26. 4/3/2020 26
FUZZIFICATION
 Use crisp inputs from the user.
 Determine membership values for all the relevant classes
(i.e., in right Universe of Discourse).

27. 4/3/2020 27
EXAMPLE - FUZZIFICATION

28. 4/3/2020 28
FUZZIFICATION OF HEIGHT

29. 4/3/2020 29
FUZZIFICATION OF WEIGHT

30. 4/3/2020 30
METHODS OF MEMBERSHIP VALUE
ASSIGNMENT
The various methods of assigning membership values are:
 Intuition,
 Inference,
 Rank ordering,
 Angular fuzzy sets,
 Neural networks,
 Genetic algorithm,
 Inductive reasoning.

31. 4/3/2020 31
FUZZY INFERENCE SYSTEMS (FIS)
 Fuzzy rule based systems, fuzzy models, and
fuzzy expert systems are also known as fuzzy
inference systems.
 The key unit of a fuzzy logic system is FIS.
 The primary work of this system is decision-
making.
 FIS uses “IF...THEN” rules along with connectors
“OR” or “AND” for making necessary decision rules.

32. 4/3/2020 32
 The input to FIS may be fuzzy or crisp, but the
output from FIS is always a fuzzy set.
 When FIS is used as a controller, it is
necessary to have crisp output.
 Hence, there should be a defuzzification unit
for converting fuzzy variables into crisp variables
along FIS.
FUZZY INFERENCE SYSTEMS

33. 4/3/2020 33
FUZZIFICATION

34. 4/3/2020 34
BLOCK DIAGRAM OF FIS

35. 4/3/2020 35
TYPES OF FIS
There are two types of Fuzzy Inference
Systems:
 Mamdani FIS(1975)
 Sugeno FIS(1985)

36. 4/3/2020 36
MAMDANI FUZZY INFERENCE
SYSTEMS (FIS)
 Fuzzify input variables:
Determine membership values.
 Evaluate rules:
Based on membership values of (composite)
antecedents.
 Aggregate rule outputs:
Unify all membership values for the output from
all rules.
 Defuzzify the output:
COG: Center of gravity (approx. by summation).

37. 4/3/2020 37
SUGENO FUZZY INFERENCE
SYSTEMS (FIS)
The main steps of the fuzzy inference process namely,
1. fuzzifying the inputs and
2. applying the fuzzy operator
are exactly the same as in MAMDANI FIS.
The main difference between Mamdani’s and Sugeno’s methods
is that Sugeno output membership functions are either linear or
constant.

38. 4/3/2020 38
SUGENO FIS

39. 4/3/2020 39
DEFUZZIFICATION
 Defuzzification is a mapping process from a space of
fuzzy control actions defined over an output universe of
discourse into a space of crisp (nonfuzzy) control
actions.
 Defuzzification is a process of converting output fuzzy
variable into a unique number .
 Defuzzification process has the capability to reduce a
fuzzy set into a crisp single-valued quantity or into a
crisp set; to convert a fuzzy matrix into a crisp matrix;
or to convert a fuzzy number into a crisp number.

40. 4/3/2020 40
FUZZY EXPERT SYSTEMS
An expert system contains three major blocks:
 Knowledge base that contains the knowledge
specific to the domain of application.
 Inference engine that uses the knowledge in the
knowledge base for performing suitable reasoning
for user’s queries.
 User interface that provides a smooth
communication between the user and the system.

41. 4/3/2020 41
BLOCK DIAGRAM OF FUZZY
EXPERT SYSTEMS
Examples of Fuzzy Expert System include
Z-II, MILORD.

42. 4/3/2020 42
SUMMARY
Defuzzification process is essential because some
engineering applications need exact values for
performing the operation.
Example: If speed of a motor has to be varied, we
cannot instruct to raise it “slightly”, “high”, etc.,
using linguistic variables; rather, it should be
specified as raise it by 200 rpm or so, i.e., a
specific amount of raise should be mentioned.
The method of defuzzification should be assessed
on the basis of the output in the context of data
available.