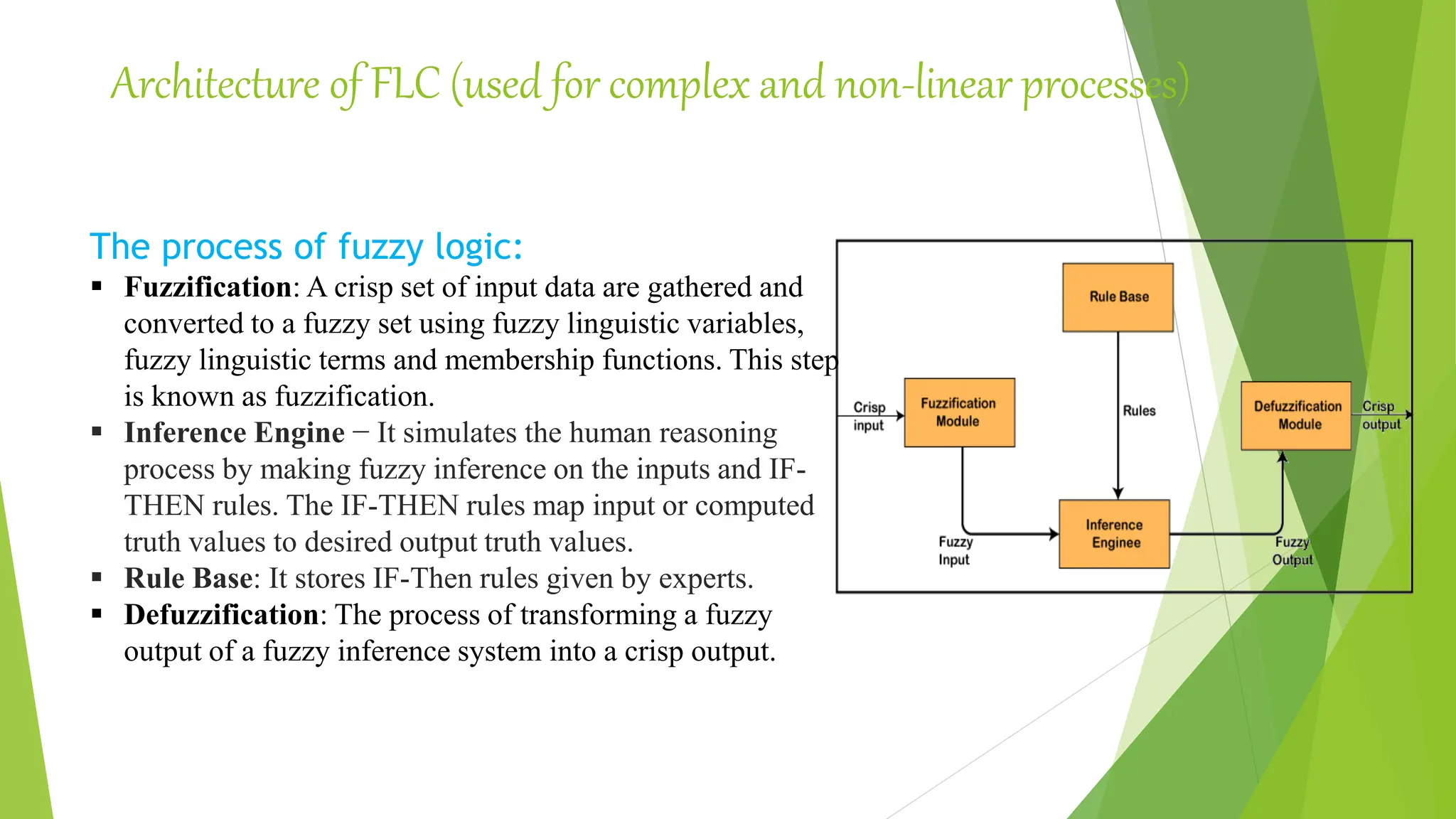
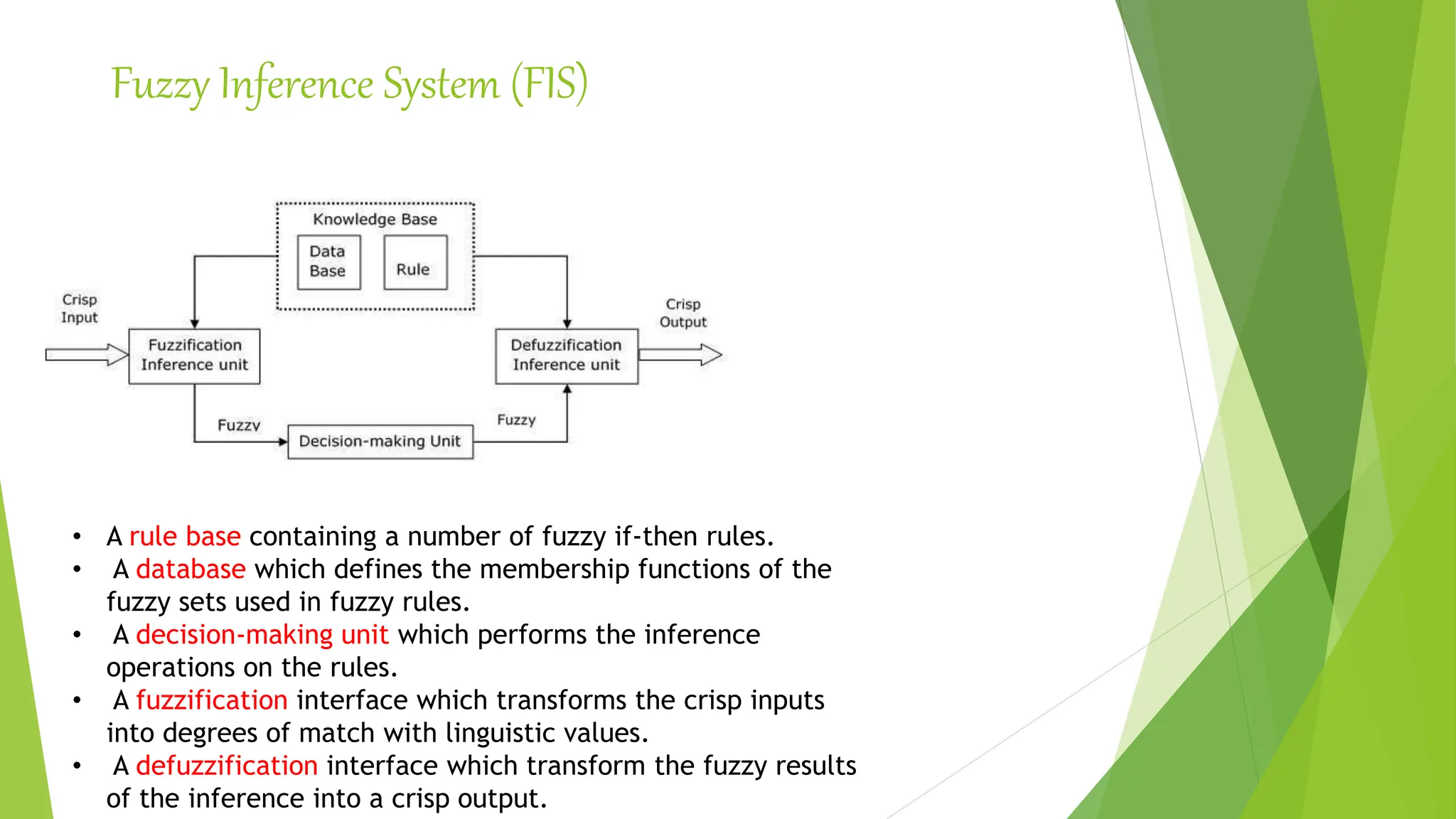
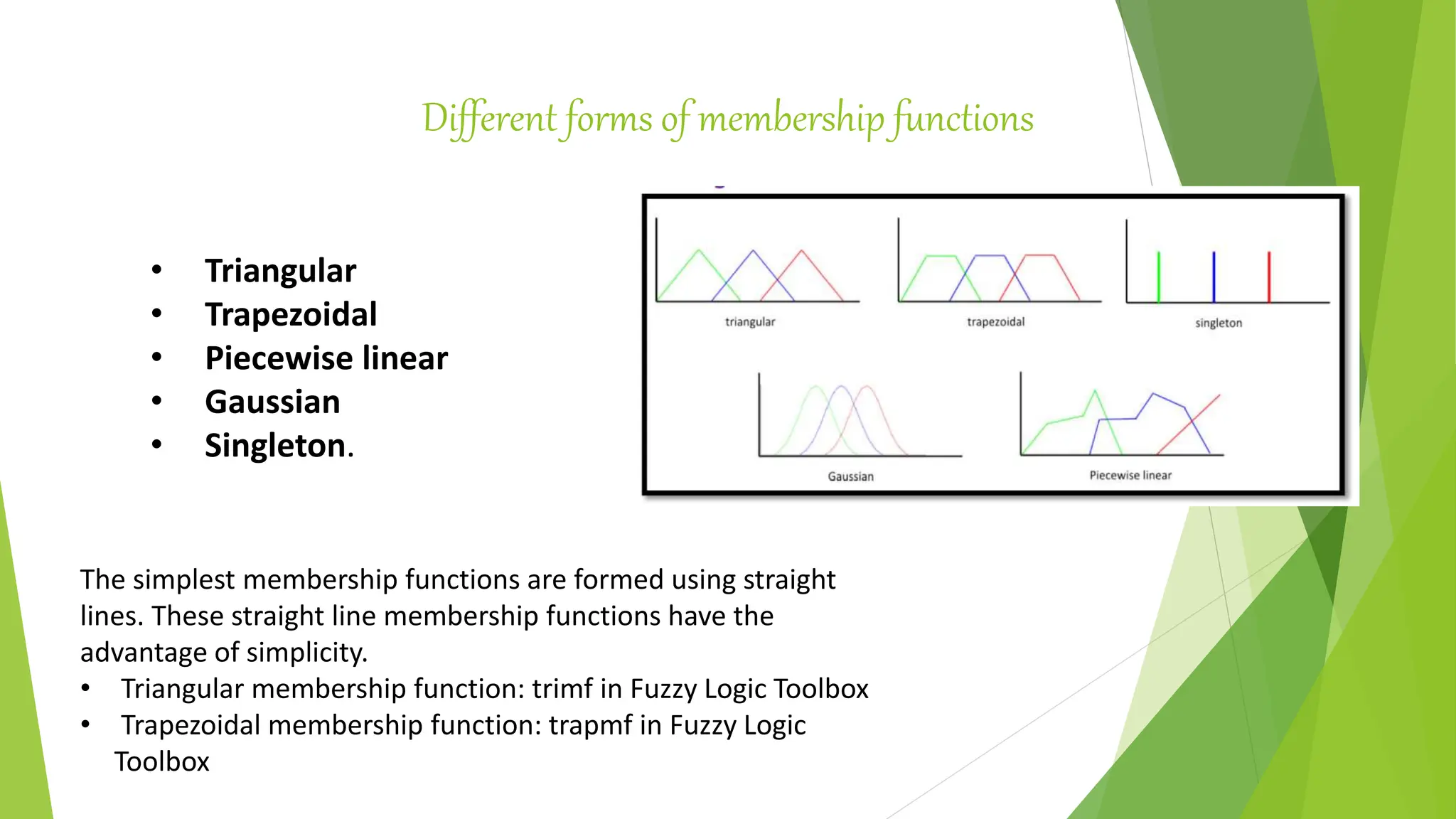
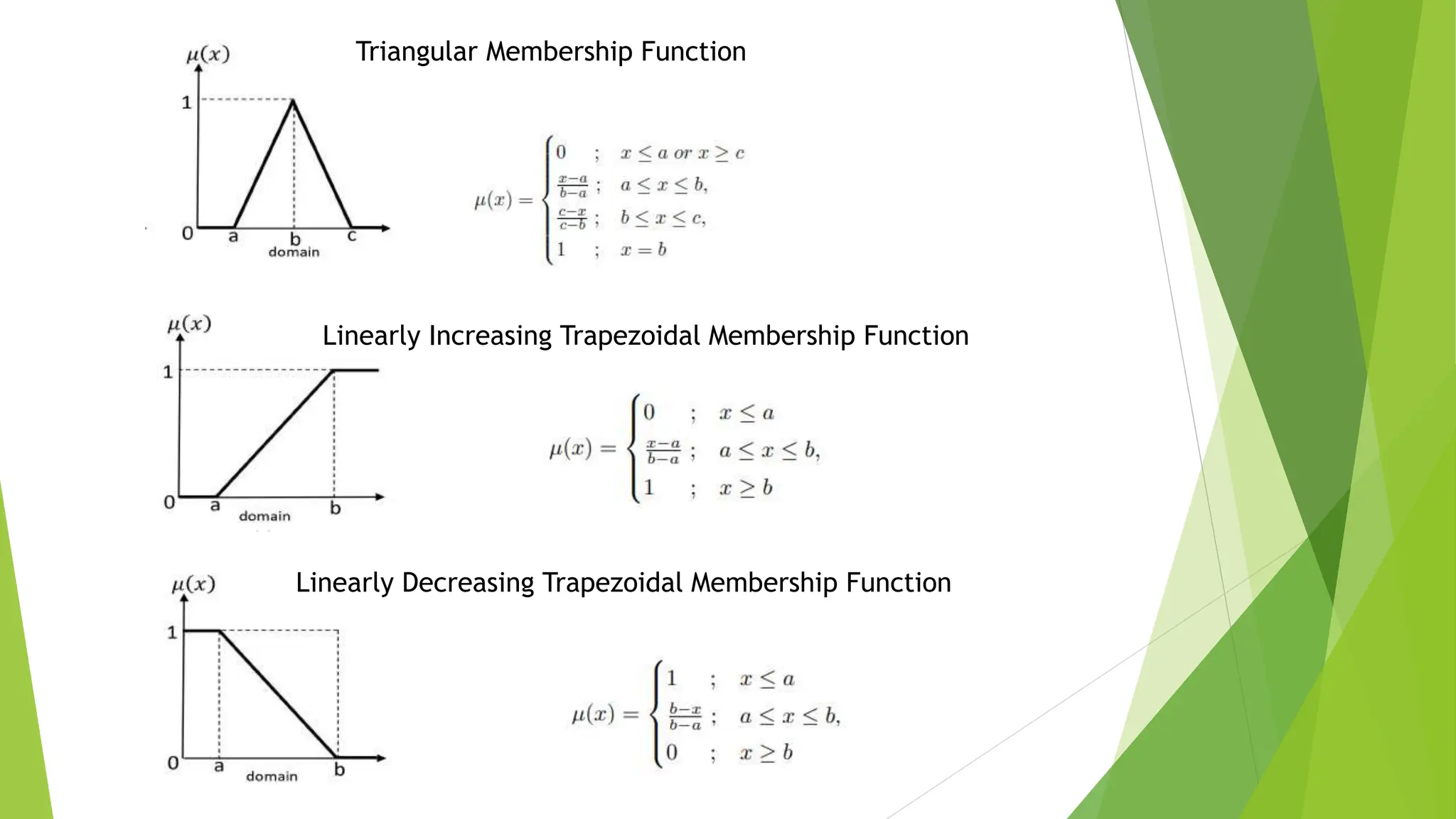
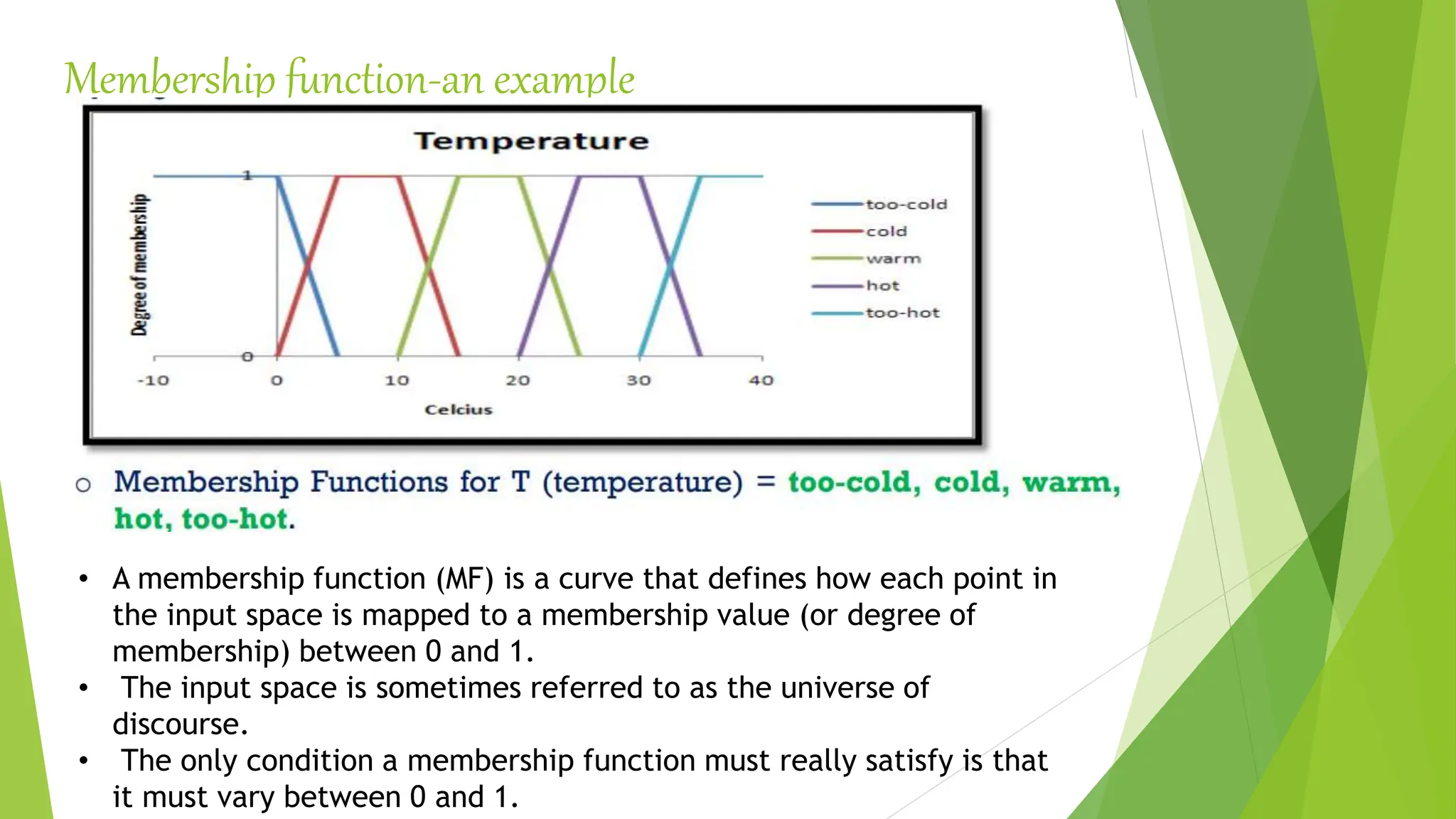
This document describes fuzzy logic controllers and their components. It discusses: - The architecture of a fuzzy logic controller including fuzzification, inference engine, rule base, and defuzzification. - Membership functions and linguistic variables which are used to quantify fuzzy sets and linguistic terms between 0 and 1. Different types of membership functions are described including triangular, trapezoidal, and Gaussian. 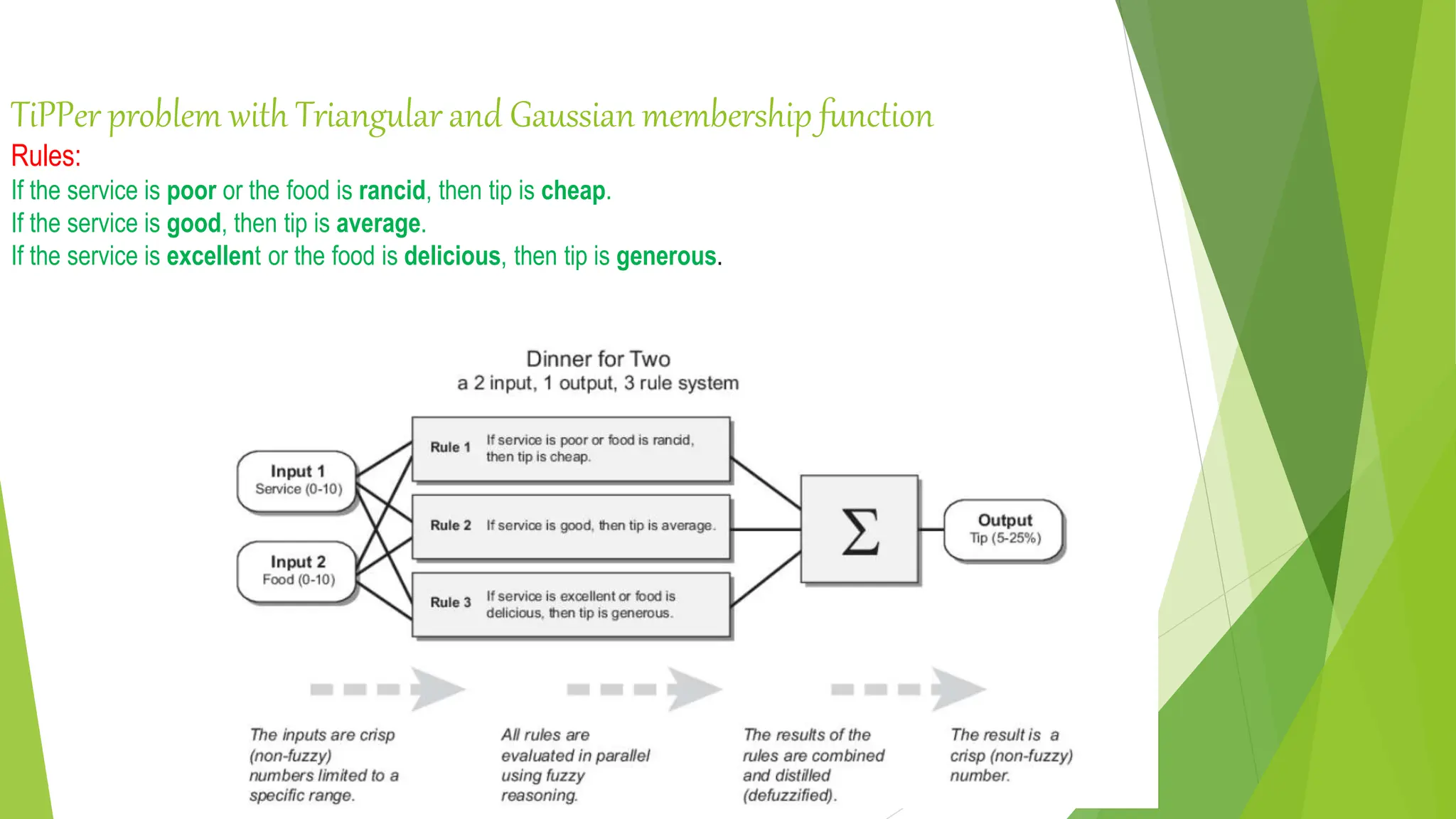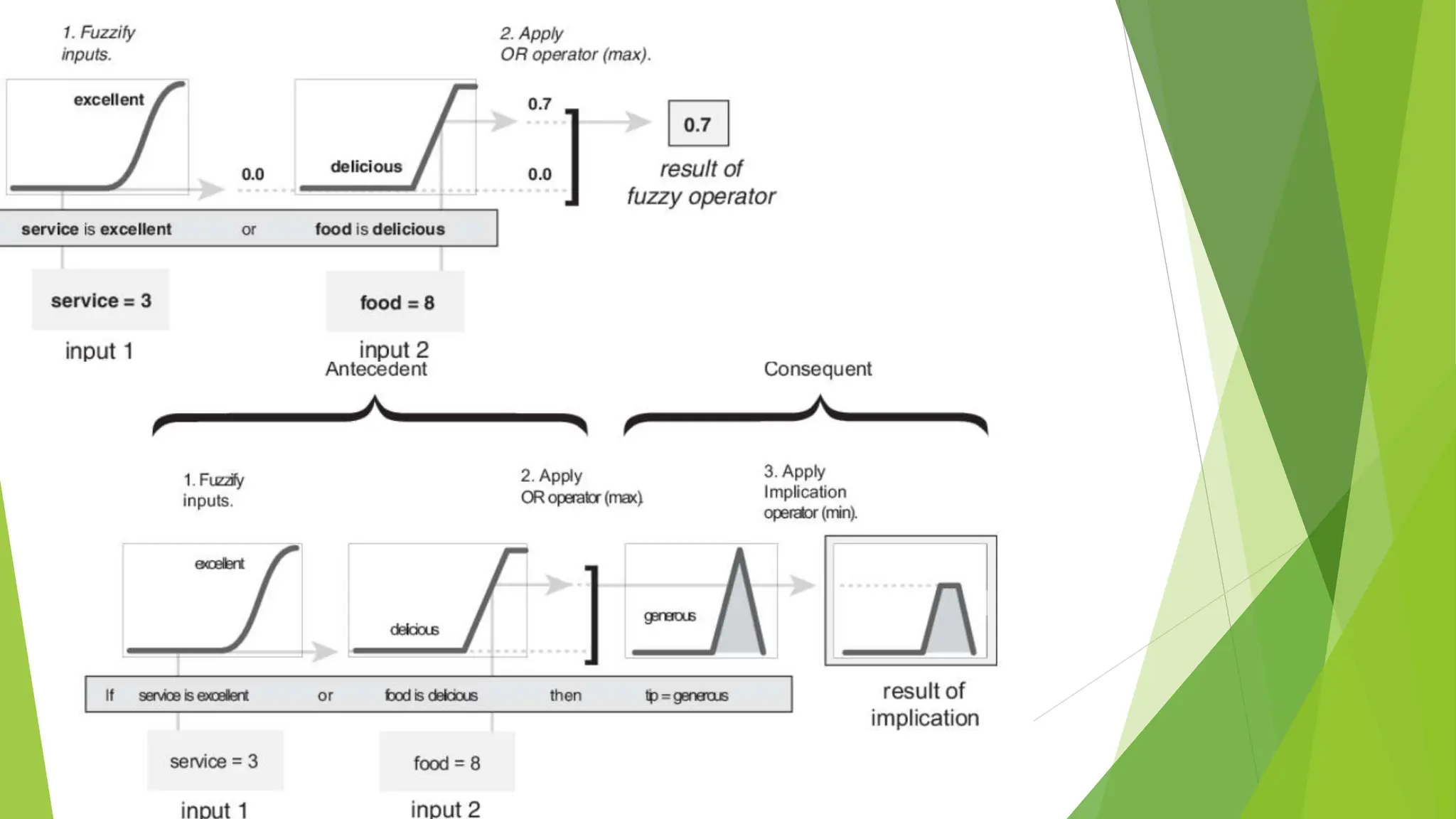- An example fuzzy logic controller for an air conditioning system that adjusts temperature based on rules relating current and target temperatures. - Implementation of a Mamdani fuzzy logic controller in MATLAB with two inputs, membership functions, a rule base, and one output to control a process.

1. Fuzzy Logic Controller

2. Example of Fuzzy Logic compared to Boolean
Fuzzy logic contains the multiple logical values and these values are the
truth values of a variable or problem between 0 and 1. This concept was
introduced by Lofti Zadeh in 1965 based on the Fuzzy Set Theory. This
concept provides the possibilities which are not given by computers, but
similar to the range of possibilities generated by humans.

4. Architecture of FLC (used for complex and non-linear processes)
The process of fuzzy logic:
 Fuzzification: A crisp set of input data are gathered and
converted to a fuzzy set using fuzzy linguistic variables,
fuzzy linguistic terms and membership functions. This step
is known as fuzzification.
 Inference Engine − It simulates the human reasoning
process by making fuzzy inference on the inputs and IF-
THEN rules. The IF-THEN rules map input or computed
truth values to desired output truth values.
 Rule Base: It stores IF-Then rules given by experts.
 Defuzzification: The process of transforming a fuzzy
output of a fuzzy inference system into a crisp output.

5. Membership Functions and Linguistic Variables
 Membership function (MF) - A function which represents the graph of fuzzy
sets that allows users to quantify the linguistic term.
 Degree of membership- The output of a membership function, this value is
always limited to between 0 and 1. Also known as a membership value or
membership grade.
 A membership function for a fuzzy set A on the universe of discourse X
is defined as μA:X → [0,1]. x axis represents the universe of discourse.
y axis represents the degrees of membership in the [0, 1] interval.
 Linguistic variables represent crisp information in a form and precision
appropriate for the problem. Each linguistic term covers a relatively wide range
of numerical values. Its value is not a number but word.

6. Different forms of membership functions
• Triangular
• Trapezoidal
• Piecewise linear
• Gaussian
• Singleton.
The simplest membership functions are formed using straight
lines. These straight line membership functions have the
advantage of simplicity.
• Triangular membership function: trimf in Fuzzy Logic Toolbox
• Trapezoidal membership function: trapmf in Fuzzy Logic
Toolbox

7. Triangular Membership Function
Linearly Increasing Trapezoidal Membership Function
Linearly Decreasing Trapezoidal Membership Function

8. Membership function-an example
• A membership function (MF) is a curve that defines how each point in
the input space is mapped to a membership value (or degree of
membership) between 0 and 1.
• The input space is sometimes referred to as the universe of
discourse.
• The only condition a membership function must really satisfy is that
it must vary between 0 and 1.

9. Membership function of Temperature with linguistic labels: Low Medium
and High
• A fuzzy logic controller describes a control protocol by
means of if-then rules, such as "if temperature is low
open heating valve slightly".
• The ambiguity (uncertainty) in the definition of the
linguistic terms (e.g., low temperature) is represented
by using fuzzy sets, which are sets with overlapping
boundaries, (as shown in the figure).
• In the fuzzy set framework, a particular domain
element can simultaneously belong to several sets
(with different degrees of membership, μ). For
instance, t=20∘C belongs to the set
of High temperatures with membership 0.4 and to the
set of Medium temperatures with membership 0.2.
• This gradual transition from one membership to
another facilitates a smooth outcome of the reasoning
(deduction) with fuzzy if-then rules.
200C =[0, 0.2, 0.4]
= [L, M, H]

10. Classical Set vs fuzzy set
 Classical set is defined in such a way that the universe of discourse is split into two
groups members and non-members. Hence, In the case of classical sets, no partial
membership exists. The membership function can be used to define a classical set A is
given by:
 Fuzzy set is a set having degrees of membership between 1 and 0. Partial membership
exists when a member of one fuzzy set can also be a part of other fuzzy sets in the same
universe. A fuzzy set A~ in the universe of discourse, X, can be defined as a set of
ordered pairs and it is given by

11. Fuzzy Logic Algorithm
1) Initialization process: Define the linguistic variables.
 Construct the fuzzy logic membership functions that define the meaning or values of
the input and output terms used in the rules.
 Construct the rule base (Break down the control problem into a series of IF X AND Y,
THEN Z rules based on the fuzzy logic rules).
2) Convert crisp input data to fuzzy values using the membership functions (fuzzification).
3) Evaluate the rules in the rule base (inference).
4) Combine the results of each rule (inference).
5) Convert the output data to non-fuzzy values (defuzzification)

12. Air conditioner system controlled by a FLS
The system adjusts the temperature of the room according to the current temperature of the room
and the target value. The fuzzy engine periodically compares the room temperature and the target
temperature, and produces a command to heat or cool the room.
For Air Conditioner example, the following rules can be used:
1) IF (temperature is cold OR too-cold) AND (target is warm) THEN command is heat.
2) IF (temperature is hot OR too-hot) AND (target is warm) THEN command is cool.
3) IF (temperature is warm) AND (target is warm) THEN command is no change.

13. Fuzzy Inference System (FIS)
• A rule base containing a number of fuzzy if-then rules.
• A database which defines the membership functions of the
fuzzy sets used in fuzzy rules.
• A decision-making unit which performs the inference
operations on the rules.
• A fuzzification interface which transforms the crisp inputs
into degrees of match with linguistic values.
• A defuzzification interface which transform the fuzzy results
of the inference into a crisp output.

14. FIS (continued)
Fuzzy if-then rules or fuzzy conditional statements are expressions of the form:
If x is A then y is B.
where, x and y are input and output variables. A and B are linguistic labels of the fuzzy sets characterized
by appropriate membership functions.
A is the antecedent and B is the consequent parts of the fuzzy rule. Fuzzy values A and B are described by
the membership functions. The forms of membership functions are different and problem depended. The
steps of fuzzy reasoning (inference operations upon fuzzy IF–THEN rules) performed by FISs are described
as follows :
 Compare the input variables with the membership functions on the antecedent part to obtain the
membership values of each linguistic label (this step is often called fuzzification).
 Combine (usually OR or max.) the membership values on the antecedent part to get firing strength
(weight) of each rule.
 Generate the qualified consequents (either fuzzy or crisp) of each rule depending on the firing
strength.
 Aggregate the qualified consequents to produce a crisp output (This step is called defuzzification).

15. TiPPer problem with Triangular and Gaussian membership function
Rules:
If the service is poor or the food is rancid, then tip is cheap.
If the service is good, then tip is average.
If the service is excellent or the food is delicious, then tip is generous.

18. TiPPer problem with triangular membership function
1. If the food is bad OR the service is poor, then the tip will be low
2. If the service is acceptable, then the tip will be medium
3. If the food is great OR the service is amazing, then the tip will be high

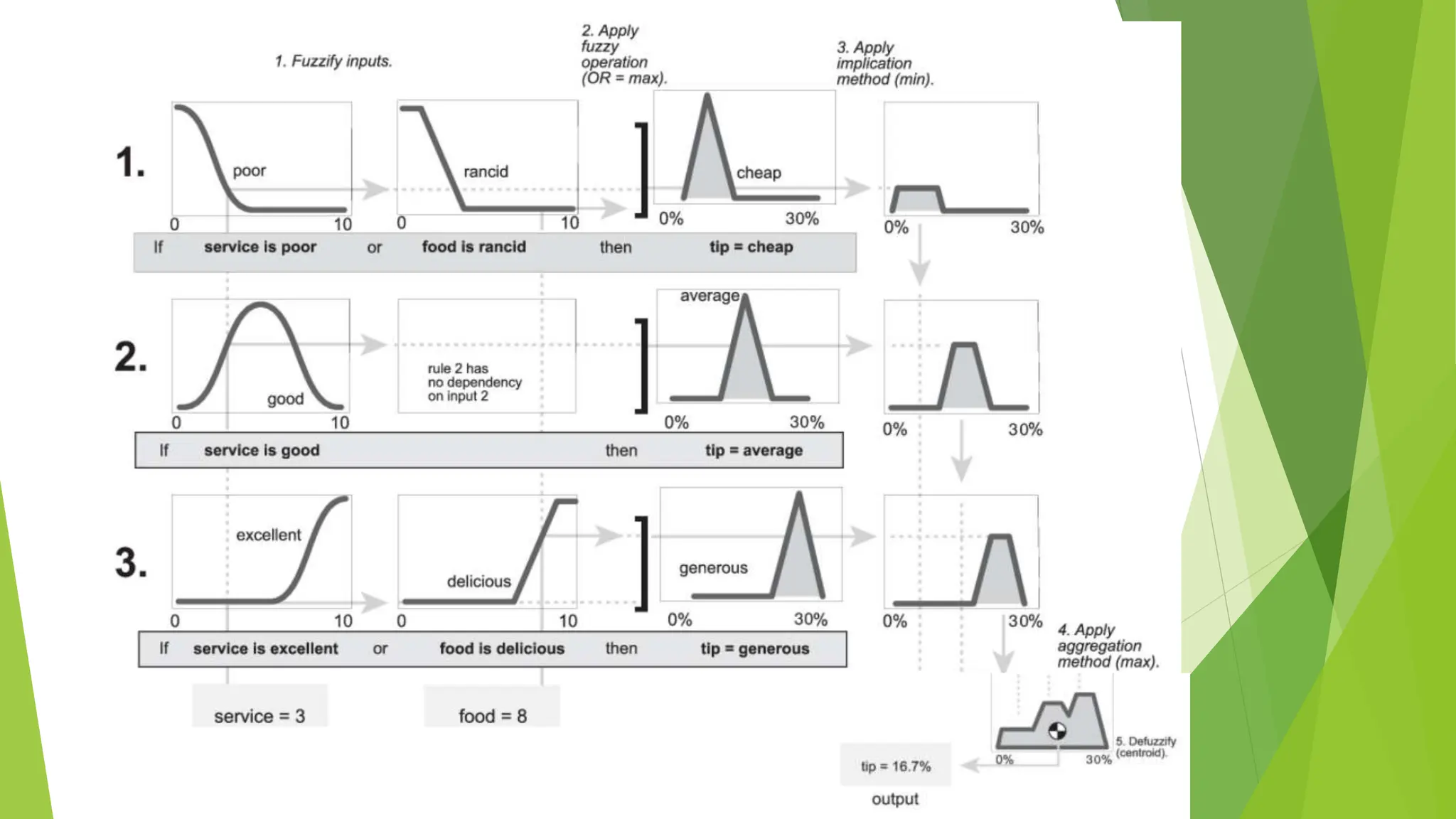
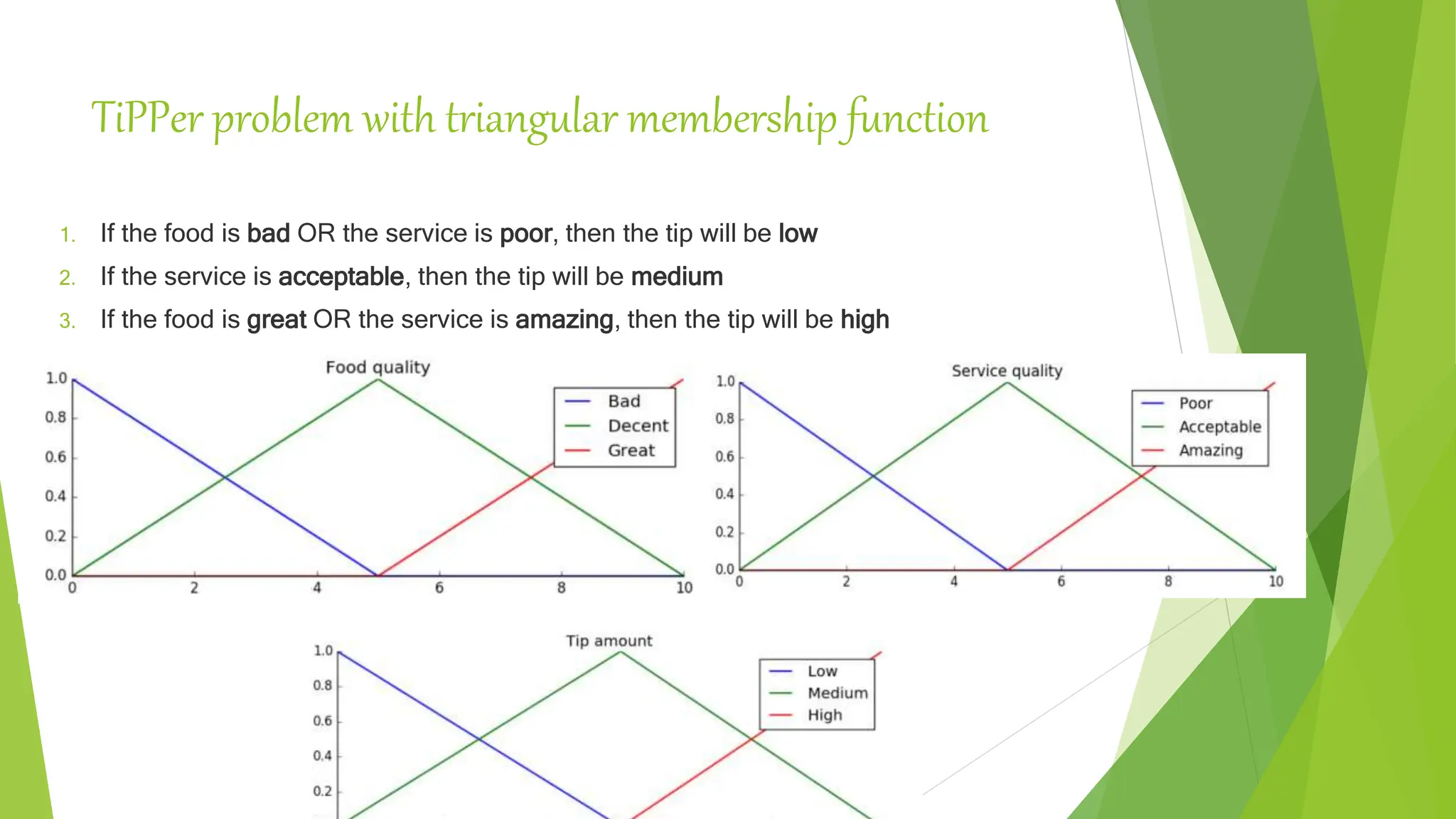
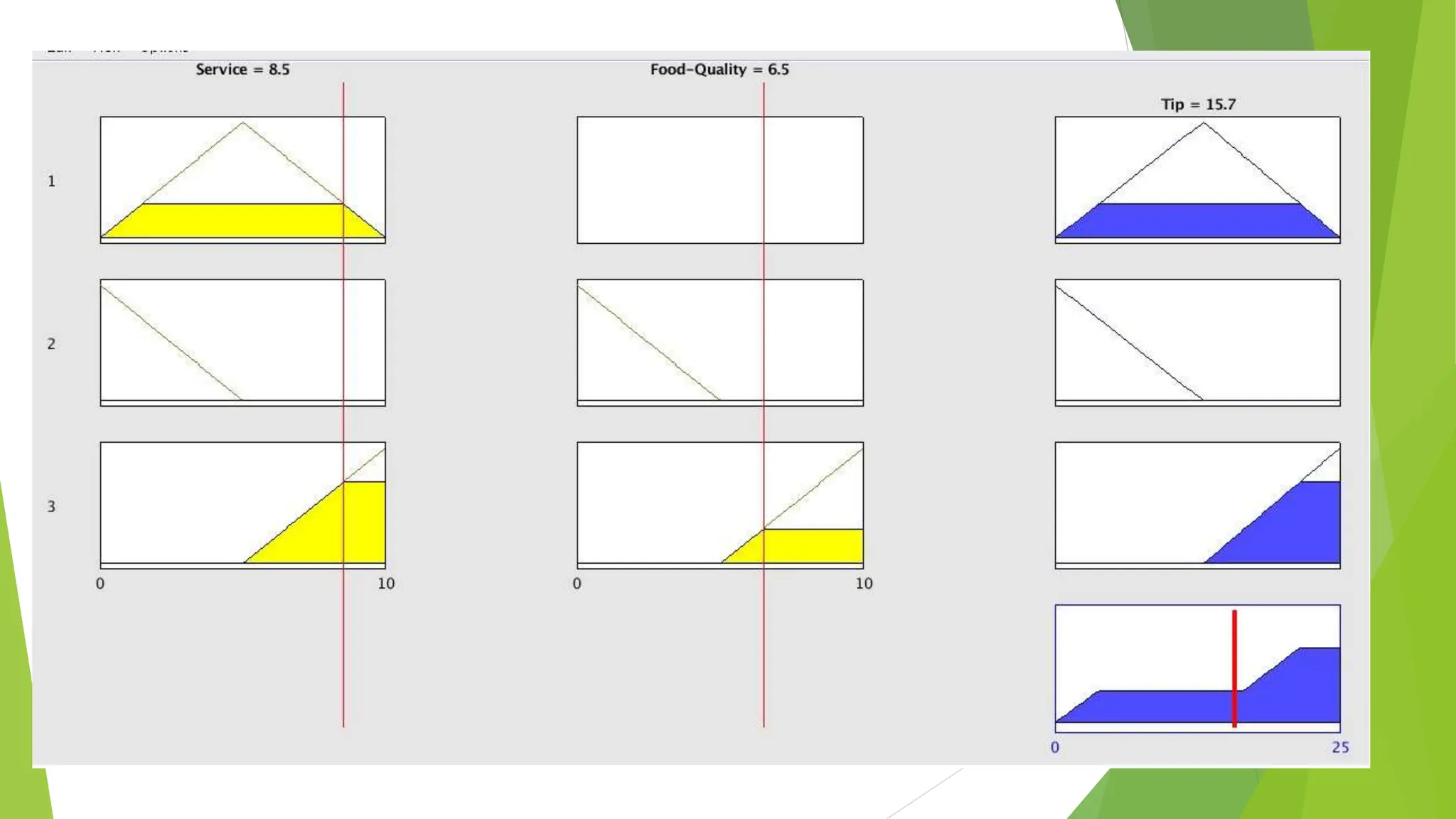
20. Comparison of Mamdani FIS and Sugeno FIS [Have et al. (2008)]
 The most fundamental difference between Mamdani-type FIS and Sugeno-type FIS
is the way the crisp output is generated from the fuzzy inputs.
 Mamdani-type FIS uses the technique of defuzzification of a fuzzy output, while
Sugeno-type FIS uses weighted average to compute the crisp output. Hence,
Mamdani FIS has output membership functions whereas Sugeno FIS has no output
membership functions.
 Mamdani type is widely accepted for capturing expert knowledge . It allows
describing the expertise in more intuitive, more human like manner.
 However, Mamdani-type entails a substantial computational burden. On the other
hand, Sugeno method is computationally efficient and works well with optimization
and adaptive techniques, which makes it very attractive in different applications.
 Mamdani-type FIS is less flexible in system design in comparison to Sugeno-type FIS
as latter can be integrated with ANFIS tool to optimize the outputs.
 The antecedent part of the rules is same for both. Only the consequent part differs.
 Mamdani is implemented on MISO and MIMO systems while Sugeno works only on
MISO systems.
 Rule base of Mamdani is of the form IF x is A and y is B THEN z is C while rule
base of Sugeno is of the form IF x is A and y is B THEN z = f(x, y).

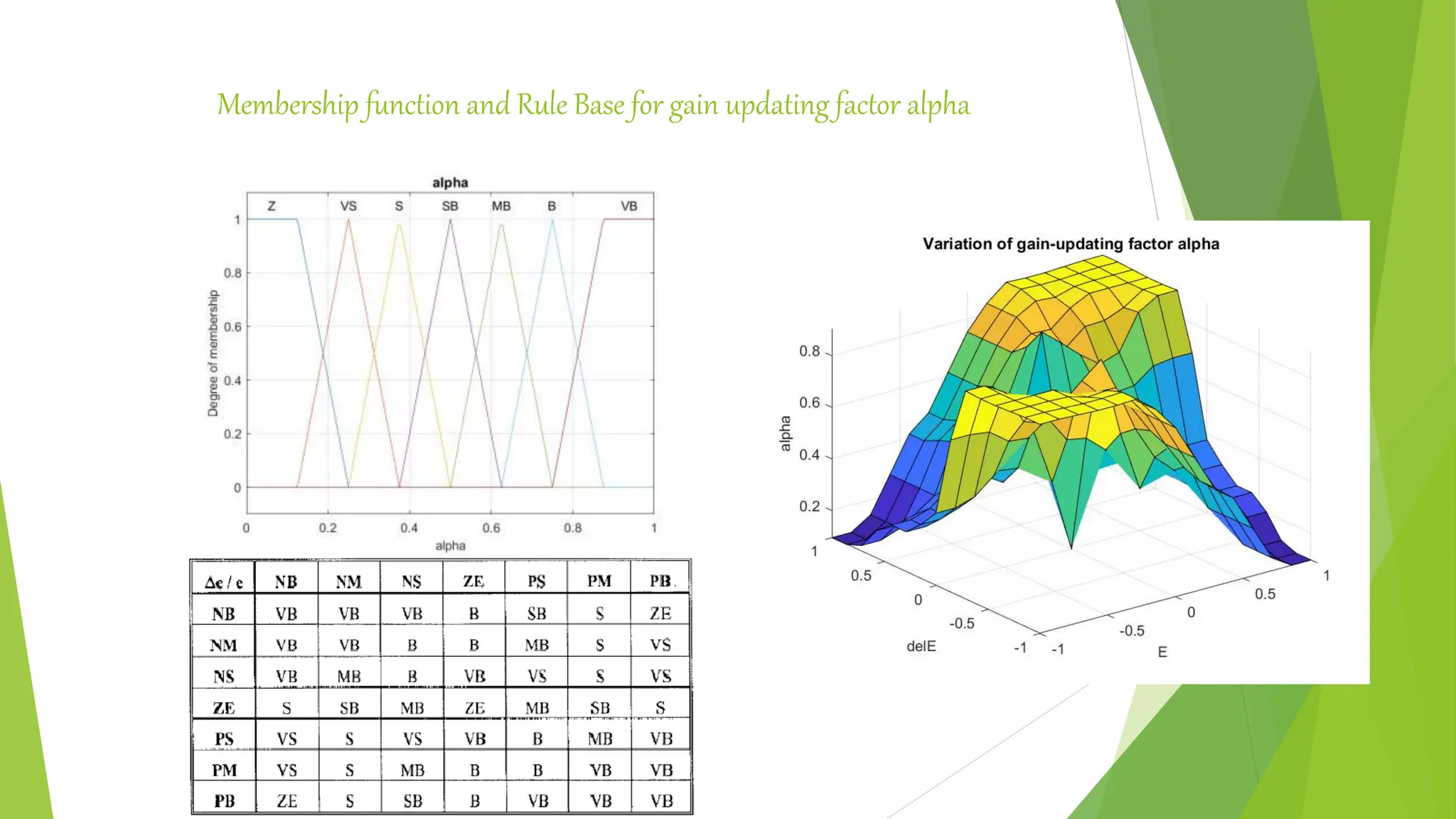
21. Models of Fuzzy Logic Controllers(FLC)
[R.Mudi et al. (2001)]
Fuzzy PI controller (commonly used)- The conventional FPIC is
described by the equation
u(k + 1) = u(k)+Δu(k)
where k is the sampling instance and Δu(k) is the incremental change in
controller output, determined by fuzzy rules of the form
“If e is E and Δe is ΔE then Δu is Δ U”
Where e and Δe are error and incremental change in error signal
respectively.
Fuzzy PD controller (not recommendable) - The fuzzy PD controller
(FPDC), on the other hand uses rules of the form :
“If e is E and Δe is ΔE then u is U”.
Fuzzy PID controller are rarely used due to the difficulties associated with
the formulation of a comparatively larger rule-base and its tuning of more
parameters.

22. Implementation of Fuzzy PI Controller
The basic control block diagram illustration with PI
type FLC
The input scaling factors (ISFs) normalize the real world inputs to a range in which membership functions
are defined. The output scaling factor (OSF) is used to change the normalized control effort to its practical
value. The relation between real and normalized values of the parameters can be simply given as
E = eke; E = Δ ekde; Δ u = Δ Uko
where E and Δ E are the normalized inputs of the FLC controller,
Δ U is the normalized FLC output;
e, Δ e are actual inputs to the FLC and Δ u is actual outputs.
ke, kde, ko are the error scaling factor, the change of error scaling factor and the control effort change
scaling factor, respectively.

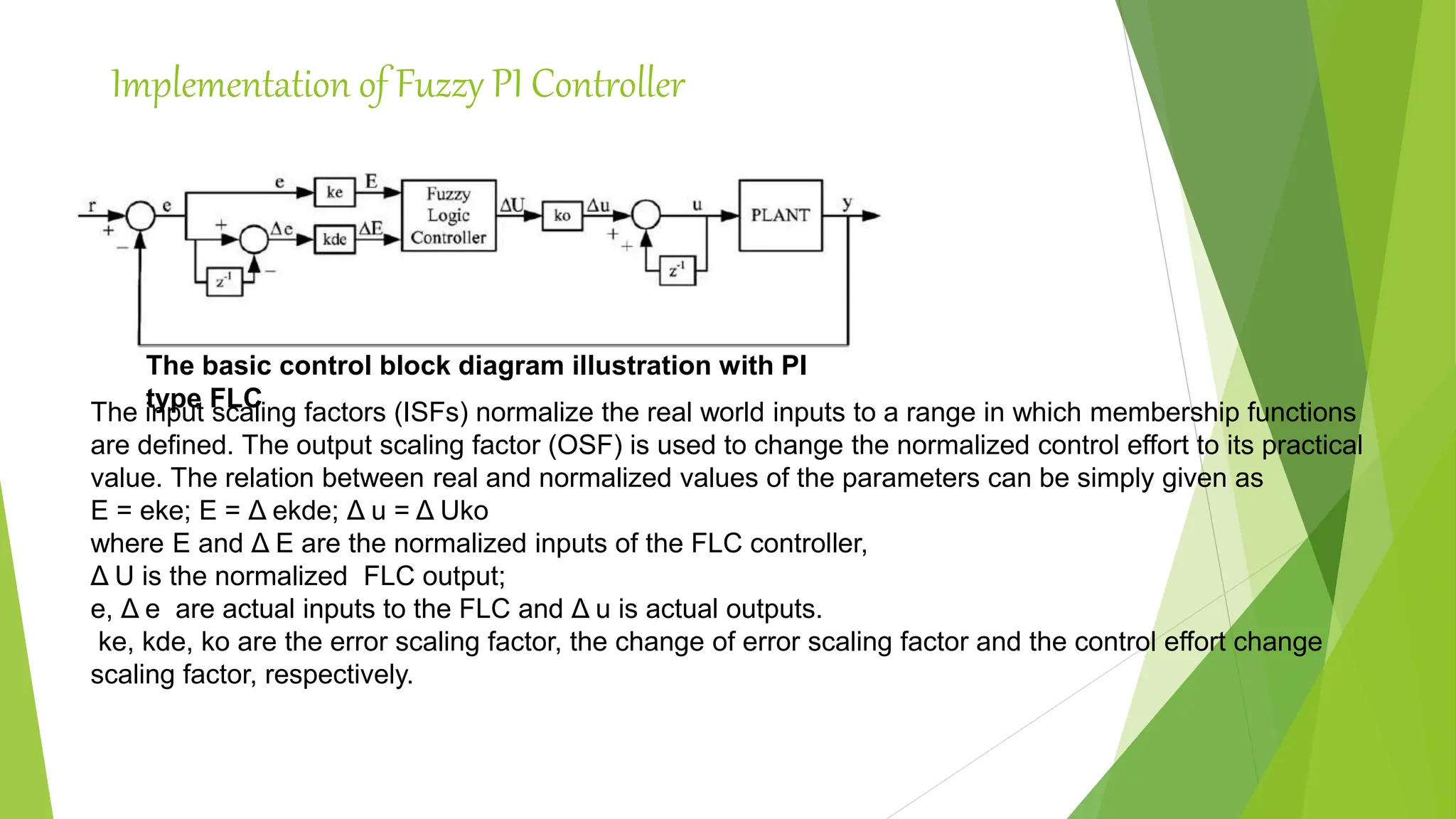
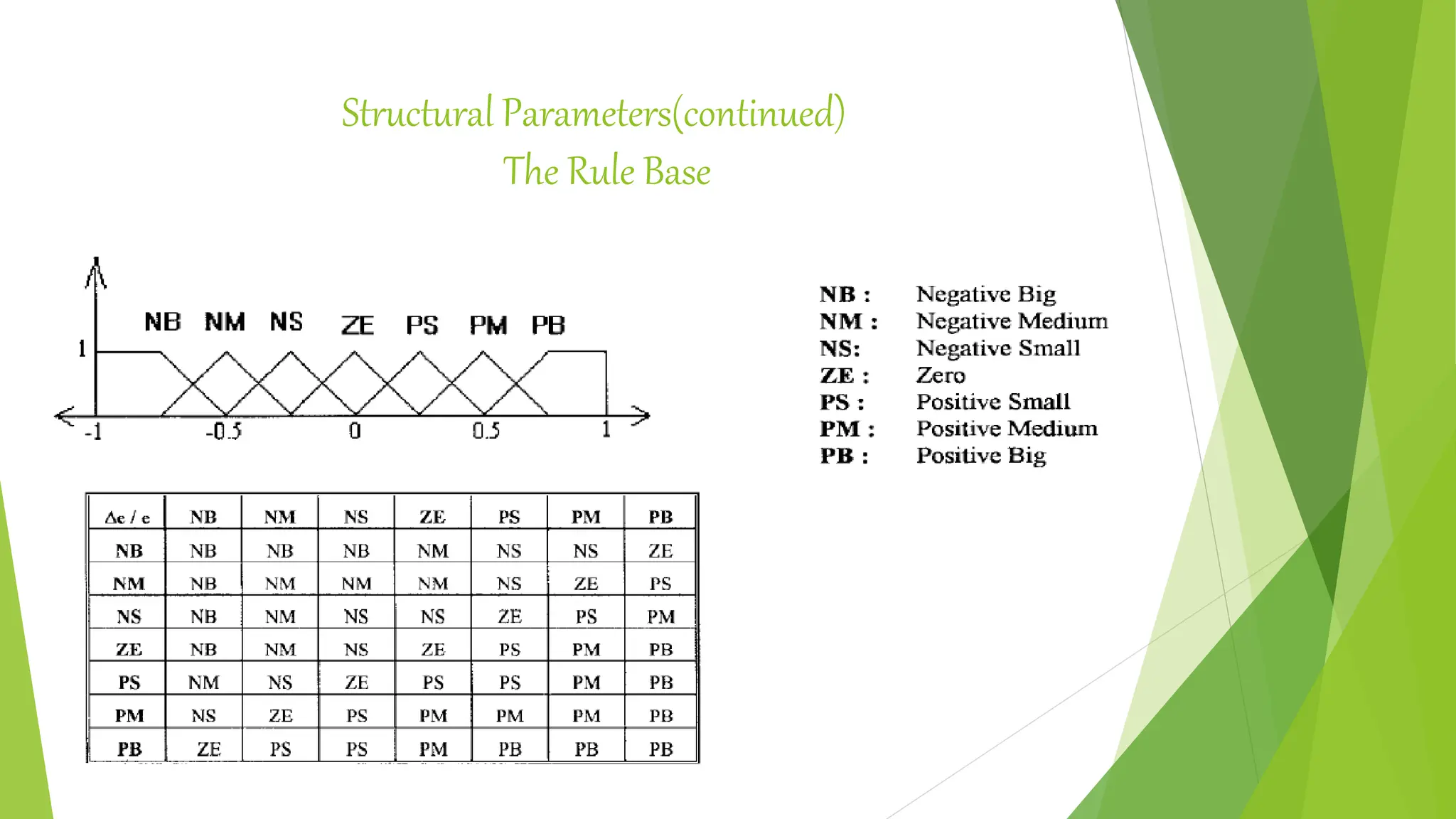
23. Detailed design considerations-Structural Parameters
(input/output (I/O) variables of fuzzy inference, fuzzy linguistic sets, membership functions, fuzzy
rules, inference mechanism and defuzzification mechanism)
[R.Mudi (1999)]
 Membership function for inputs (e, Δ e ) and output (Δ u )
 The input variables are decomposed into at least seven fuzzy linguistic levels in
order to make a considerable distinction between the fuzzy regions and, thus,
to obtain fine tuned control action.
 The universe of discourse is chosen to be[-1, 1] for the membership functions of
input and output variables.
 The input and output parameters are scaled to fit this range via scaling factors.
 We use symmetric triangles (except the two MF’s at the extreme ends) with equal base
and 50% overlap with neighboring MF’s as shown in the figure below. This is the most
natural and unbiased choice for MF’s.

24. Structural Parameters(continued)
The Rule Base

25. Formulation of Rule Base
In the PM error region, when the error rate is Z, the plant is in an undershoot state and the FLC is generating a
medium control action to reduce undershoot and drive the plant back toward the desired output. The remaining
rules are developed in a similar manner. Each rule has the form of:
IF "e is label I" AND "ae is label 2"THEN "output is label 3"
Zone Orange- In this zone error has a tendency to increase further, so a large control action is
required. It affects rise time and overshoot/undershoot of the system
Zone Green- In this zone error has a tendency to reduce further, so a small control action is
required. It affects rise time of the system.
Zone Pink-Both error and change of error is small, so small control action is required. It affects

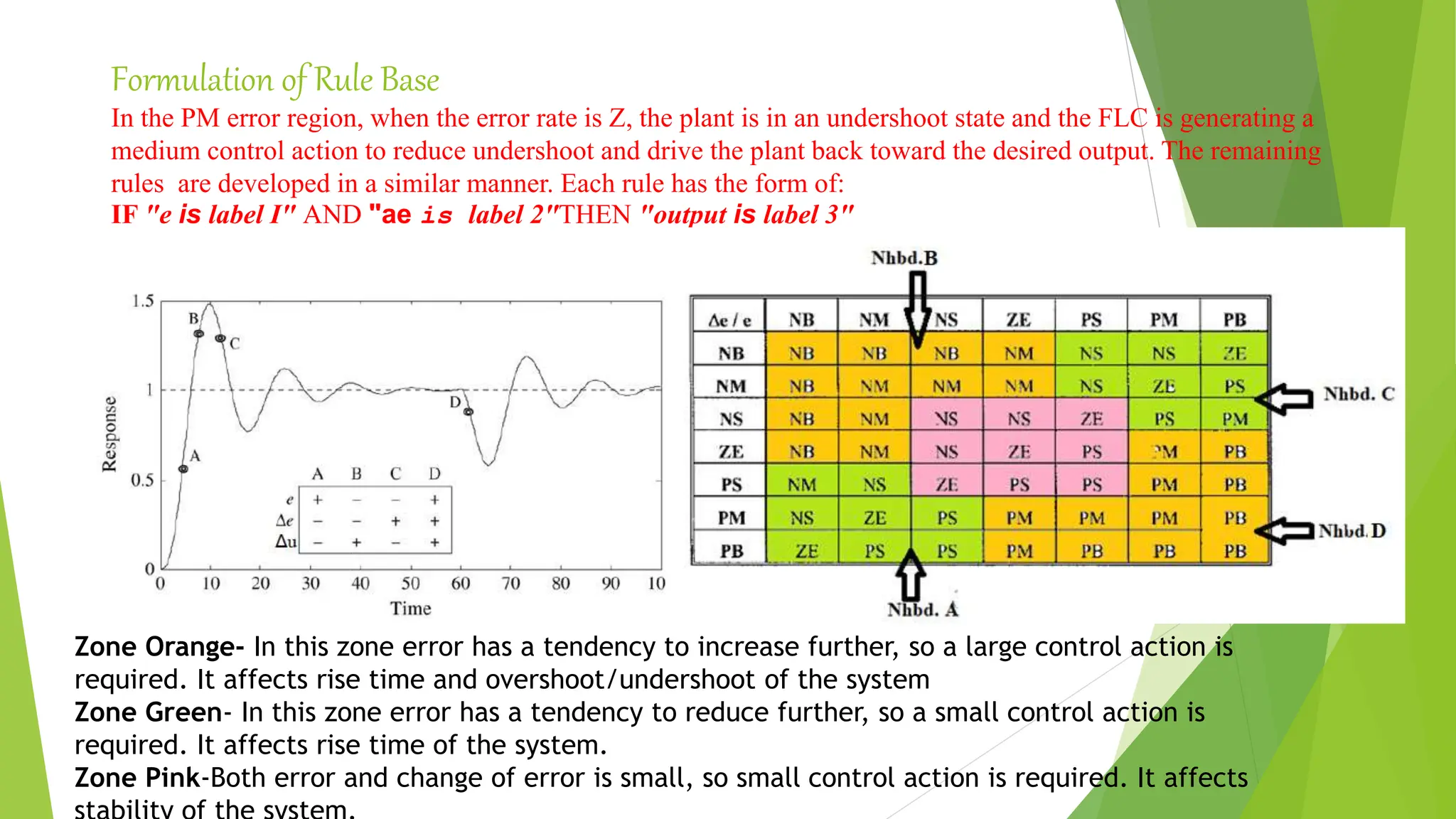
26. Detailed design considerations-Tuning Parameters(scaling factor(SF),
membership function(MF) and rules
Tune the parameters of PI-type FLC’s in order of their significance; that is, first
parameters with a global effect (SF) and then ones with only local effect (MF and
rules) and, hence, given the maximum importance to the tuning of SF’s.
 Scaling Factor: The values of the actual inputs are mapped onto [ -1, 1] by the input SF’s and , the
controller output is mapped onto the respective actual output or domain by the output SF by trial and error.
Tuning the SF affects all the rules of the rule base .
Tuning Scaling factor

27. Detailed design considerations-Tuning Parameters(scaling factor(SF), membership
function(MF) and rules (continued)
 Membership Function: Tuning a peak value or width of a MF affects only the rule which uses
the label. It shows a marginal improvement in transient response of a second order system.
Tuning peak or width of MF of if-part of variable Tuning peak or width of then-part of variable
 Rule: When rule is changed only the rule involved changes.
Tuning a rule

28. MAMDANI FIS IN MATLAB WITH TWO INPUTS
AND ONE OUTPUTS (WITH THREE LINGUISTIC
LABELS)

29. fis1 = mamfis;
%Membership function for inputs 'error' and 'change of error'
fis1 = addInput(fis1,[0 0.2],'Name','E');
fis1 = addInput(fis1,[0 0.8],'Name','delE');
fis1 = addMF(fis1,'E','trimf',1*[0 0.04 0.08],'Name','L');
fis1 = addMF(fis1,'E','trimf',1*[0.06 0.1 0.14],'Name','M');
fis1 = addMF(fis1,'E','trimf',1*[0.12 0.16 0.2],'Name','H');
fis1 = addMF(fis1,'delE','trimf',1*[0 0.15 0.3],'Name','L');
fis1 = addMF(fis1,'delE','trimf',1*[0.25 0.4
0.55],'Name','M');
fis1 = addMF(fis1,'delE','trimf',1*[0.5 0.650.8],'Name','H');
figure
subplot(1,3,1)
plotmf(fis1,'input',1)
title('error')
subplot(1,3,2)
plotmf(fis1,'input',2)
title('error change')
%Membership function for output control signal'U'
fis1 = addOutput(fis1,[0 1],'Name','U');
fis1 = addMF(fis1,'U','trimf',1*[0 0.15 0.3],'Name','L');
fis1 = addMF(fis1,'U','trimf',1*[0.25 0.4 0.55],'Name','M');
fis1 = addMF(fis1,'U','trimf',1*[0.55 0.65 0.8],'Name','H');

30. subplot(1,3,3)
plotmf(fis1,'output',1)
title('U')
% form Rule Base
rules = [...
"E==L & delE==L => U=L"; ...
"E==L & delE==M => U=M"; ...
"E==L & delE==H => U=M"; ...
"E==M & delE==L => U=L"; ...
"E==M & delE==M => U=M"; ...
"E==M & delE==H => U=H"; ...
"E==H & delE==L => U=M"; ...
"E==H & delE==M => U=M"; ...
"E==H & delE==H => U=H" ...
];
fis1 = addRule(fis1,rules);
figure
gensurf(fis1)
title('Variation of output U with inputs error and
change of error')
figure
plotfis(fis1)
writeFIS(fis1,'myFile')

31. MAMDANI FIS in MATLAB
 Selected two inputs for Error as ‘E’ and change of Error as ‘delE’ and one output as ‘U’.
 Defined triangular membership functions in the universe of discourse [-1,1]. Each
membership has seven linguistic labels.
fis1 = mamfis;
%Membership function for inputs 'error' and 'change of error'
fis1 = addInput(fis1,[-1 1],'Name','E');
fis1 = addInput(fis1,[-1 1],'Name','delE');
fis1 = addMF(fis1,'E','trimf',[-1.32 -1 -0.66],'Name','NL');
fis1 = addMF(fis1,'E','trimf',[-1 -0.66 -0.33],'Name','NM');

32. MAMDANI FIS in MATLAB
% form Rule Base
rules = [...
"E==NL & delE==PL => U=Z"; ...
"E==NL & delE==PM => U=NS"; ...
"E==NL & delE==PS => U=NM"; ...
"E==NL & delE==Z => U=NL"; ...
];
fis1 = addRule(fis1,rules);
gensurf(fis1)
title('Control surface of conventional FLC')
writeFIS(fis1,'myFile')

33. Simulation of conventional PID and PI-FLC in Simulink

34. Response of FLC and PID obtained from Simulink
Simulation
The plant is a SOPDT system whose
transfer function is
G s = Ke−tds ωn
2
s2+2ξωn s+ωn
2
K=1, td=0.08 sec, ωn =1 rad/sec, ξ=0.75

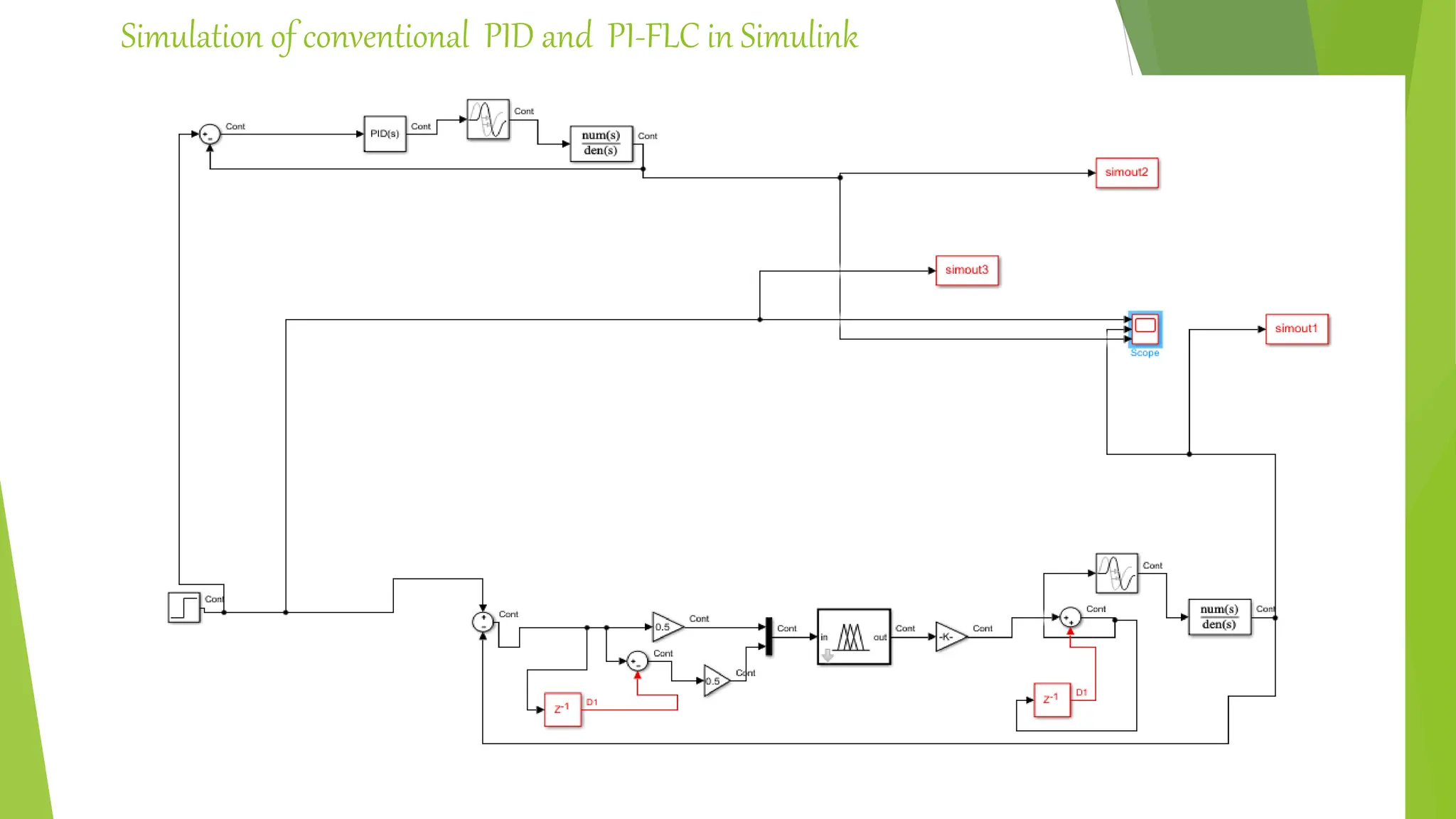
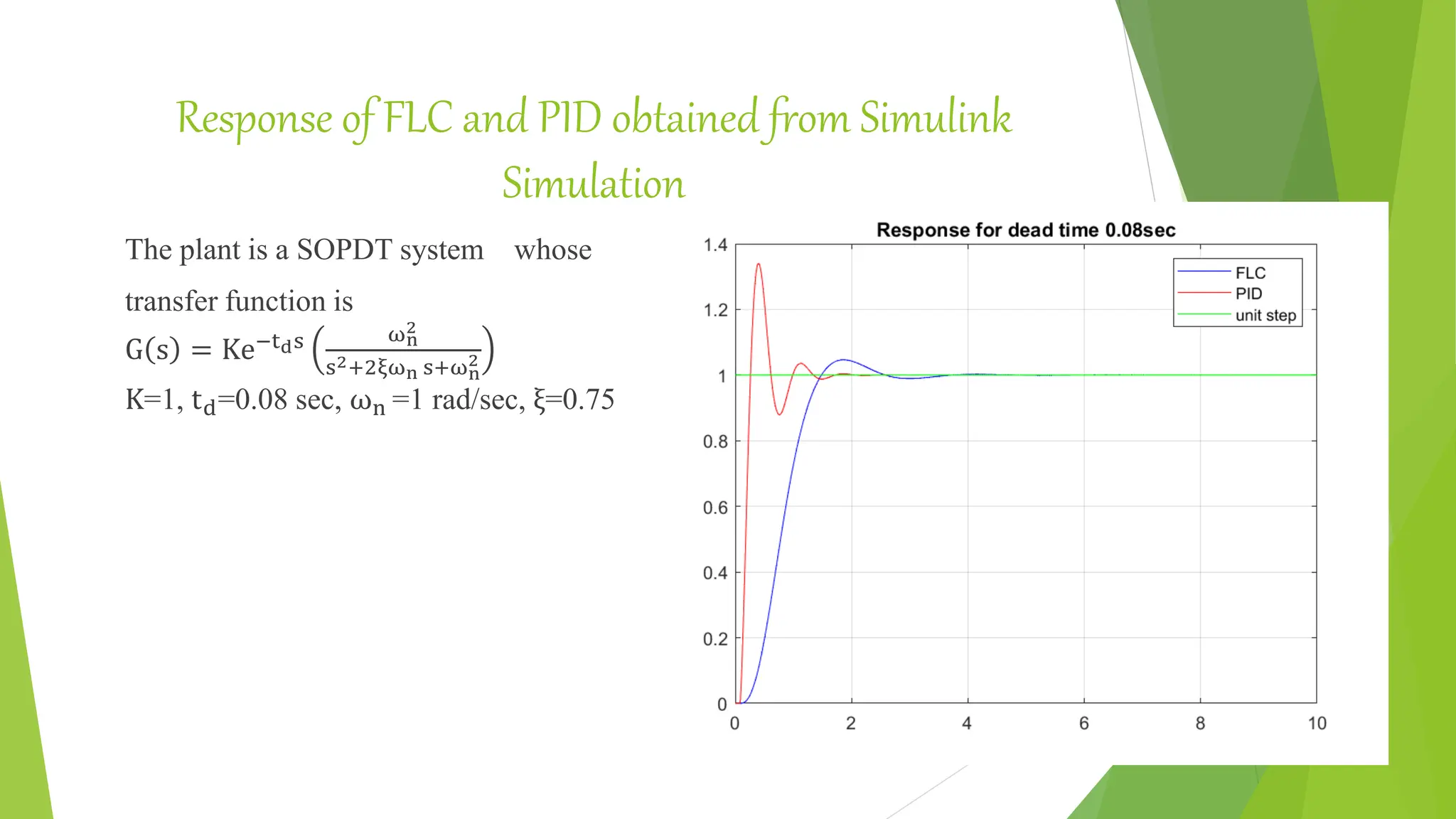
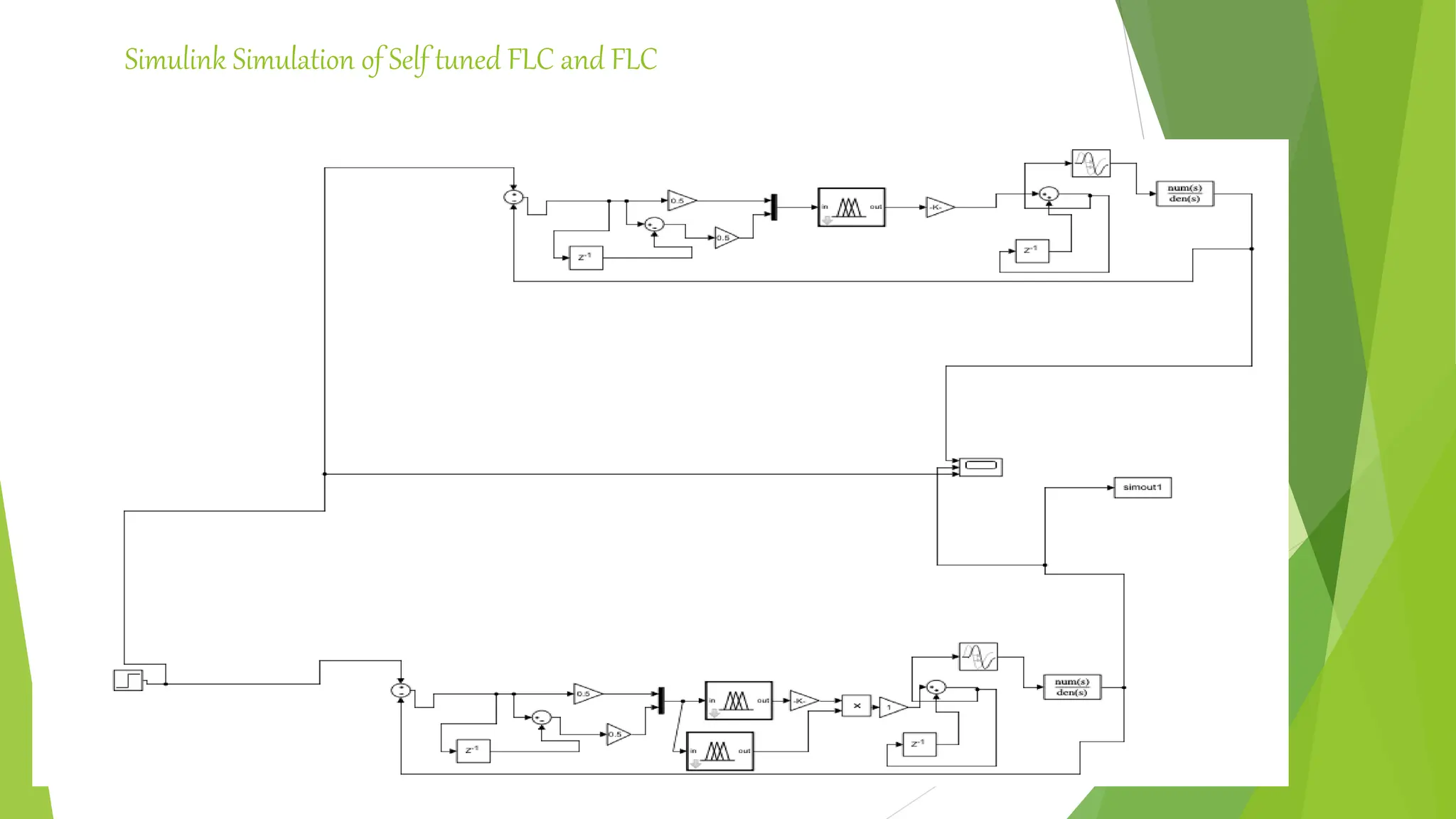
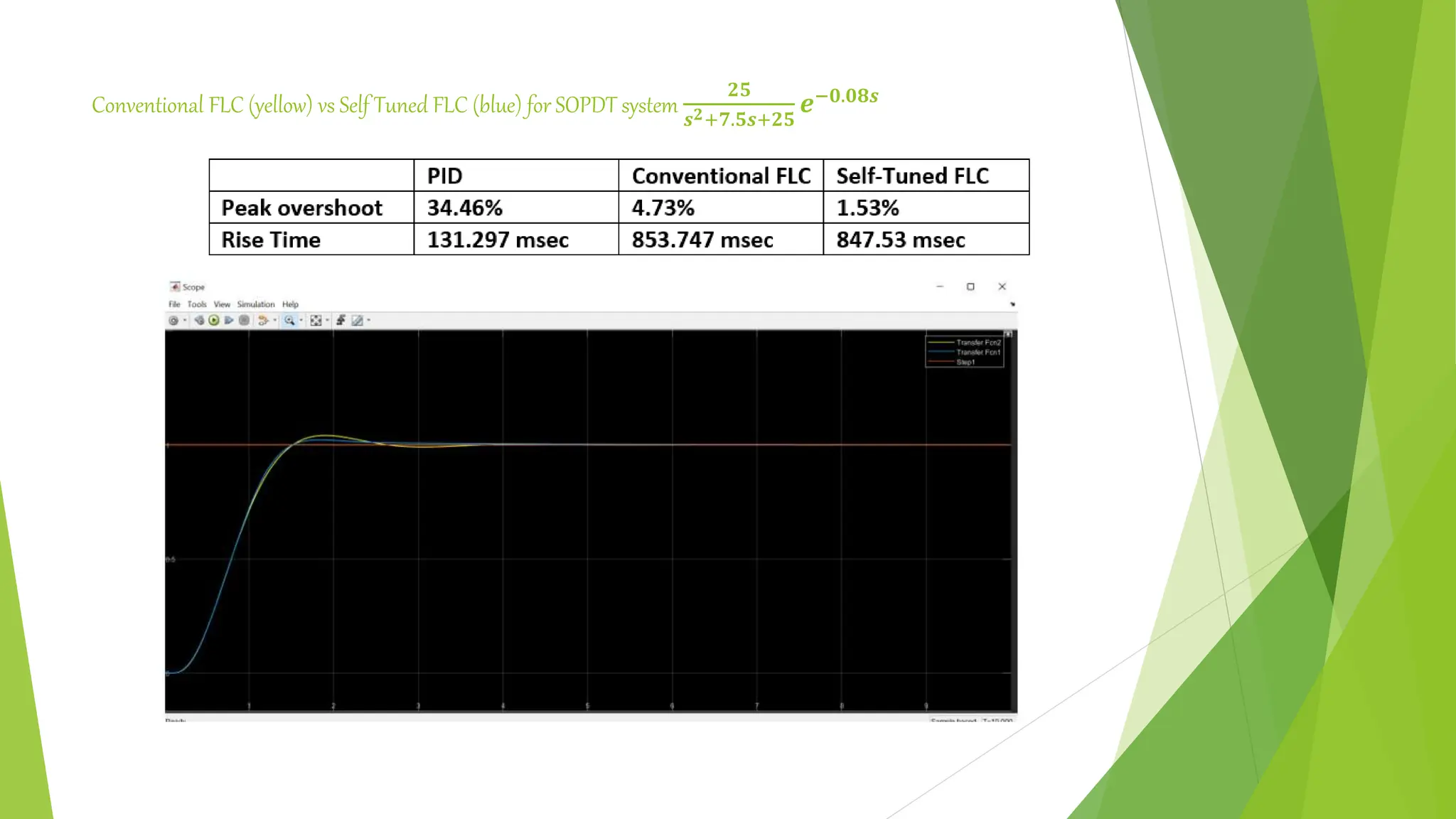
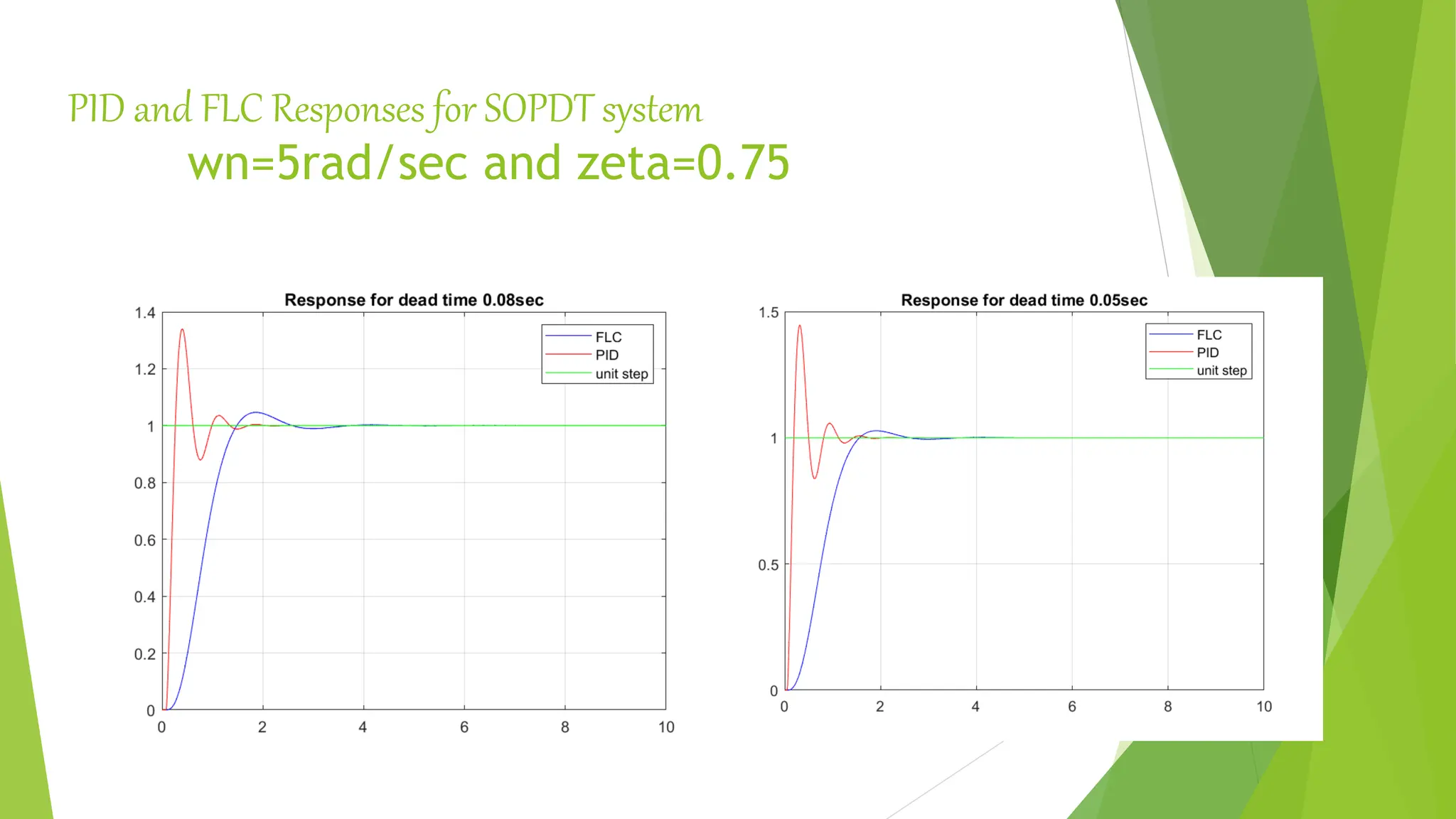
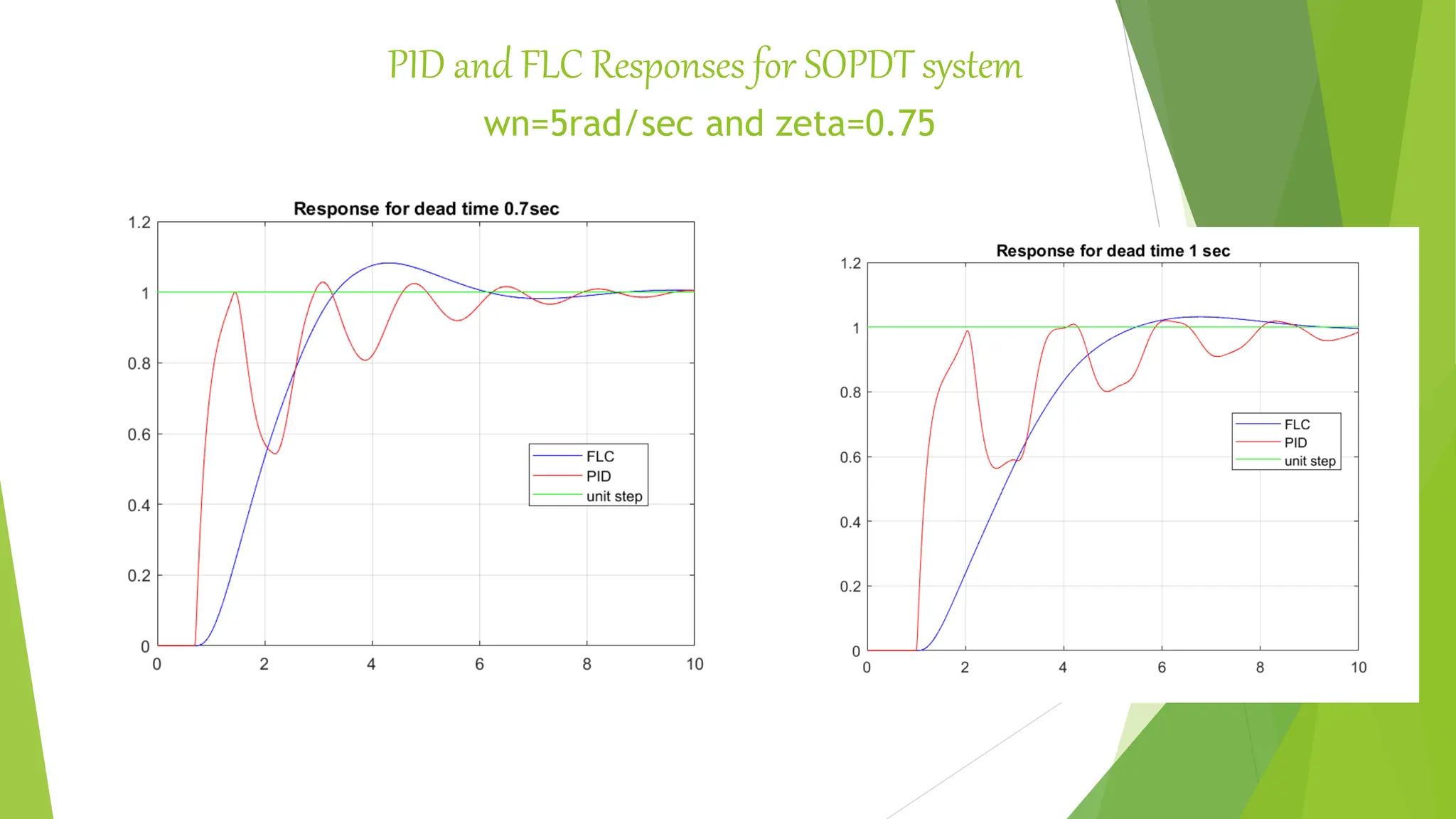
35. Simulink Simulation of PID and Self Tuned FLC [R.Mudi et al.( 1999)]

36. Membership function and Rule Base for gain updating factor alpha

37. Simulink Simulation of Self tuned FLC and FLC

38. Conventional FLC (yellow) vs Self Tuned FLC (blue) for SOPDT system
𝟐𝟓
𝒔𝟐+𝟕.𝟓𝒔+𝟐𝟓
𝒆−𝟎.𝟎𝟖𝒔

39. PID and FLC Responses for SOPDT system
wn=5rad/sec and zeta=0.75

40. PID and FLC Responses for SOPDT system
wn=5rad/sec and zeta=0.75

41. Reference
 A. Hamam and N. D. Georganas, “A Comparison of Mamdani and Sugeno Fuzzy
Inference Systems for Evaluating the Quality of Experience of Hapto-Audio-Visual
Applications” HAVE 2008 – IEEE International Workshop on Haptic Audio Visual
Environments and their ApplicationsOttawa Canada, 18-19 October 2008.
 Rajani K. Mudi and Nikhil R. Pal, “A note on fuzzy PI-type controllers with resetting
action”, Elsevier, Fuzzy Sets and Systems 121 (2001) 149–159.
 Rajani K. Mudi and Nikhil R. Pal, “A Robust Self-Tuning Scheme for PI- and PD-Type
Fuzzy Controllers” IEEE Transactions on Fuzzy Systems, VOL. 7, NO. 1, February 1999.
 L. Zheng, “A practical guide to tune of proportional and integral (PI)like fuzzy controllers,”
in Proc. Fuzz IEEE, San Diego, CA, Mar. 1992,pp. 633–641.
 Hakkı Murat Genc , Engin Yesil , Ibrahim Eksin , Mujde Guzelkaya , Ozgur Aydın
Tekin ,” A rule base modification scheme in fuzzy controllers for time-delay systems”
Expert Systems with Applications 36 (2009) 8476–8486

42. THANK YOU