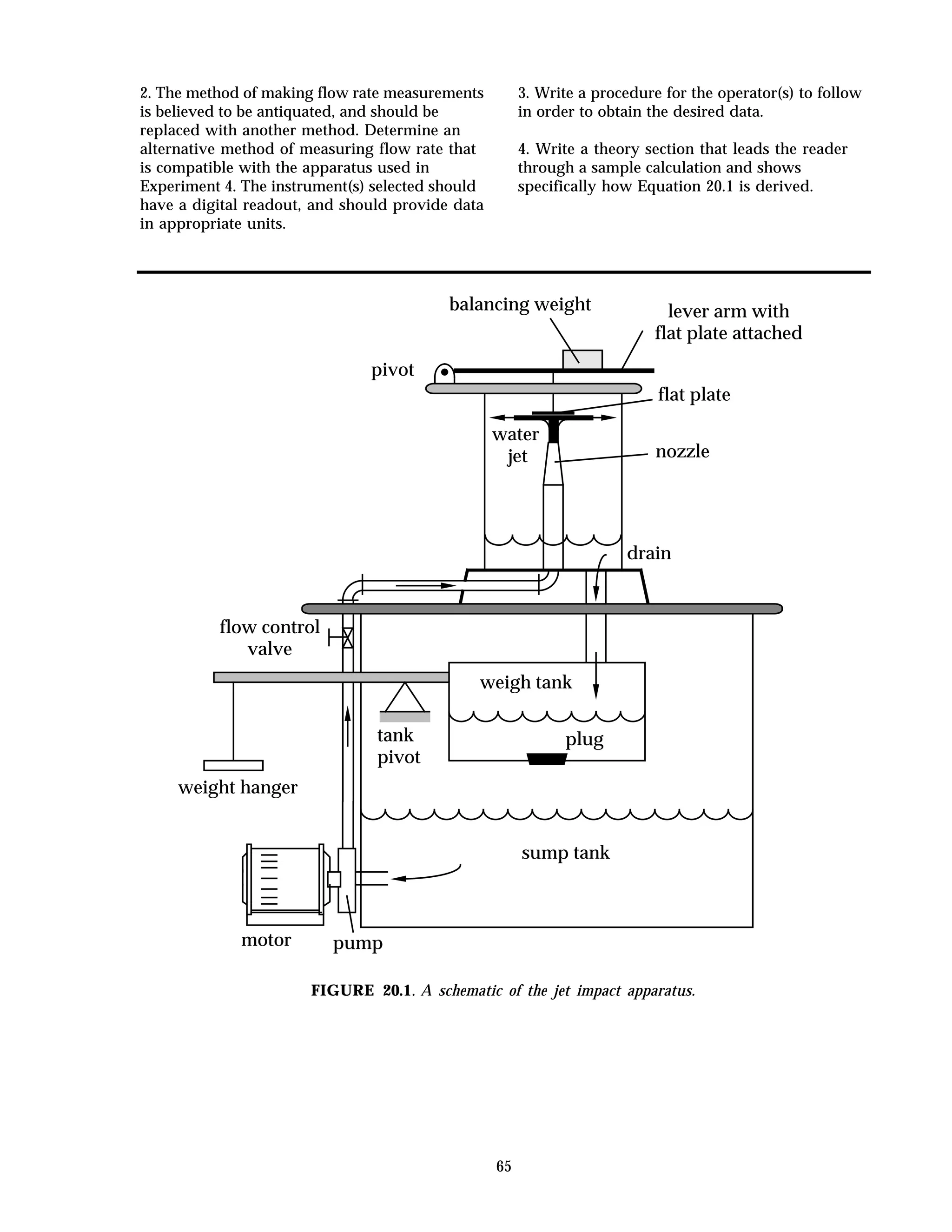
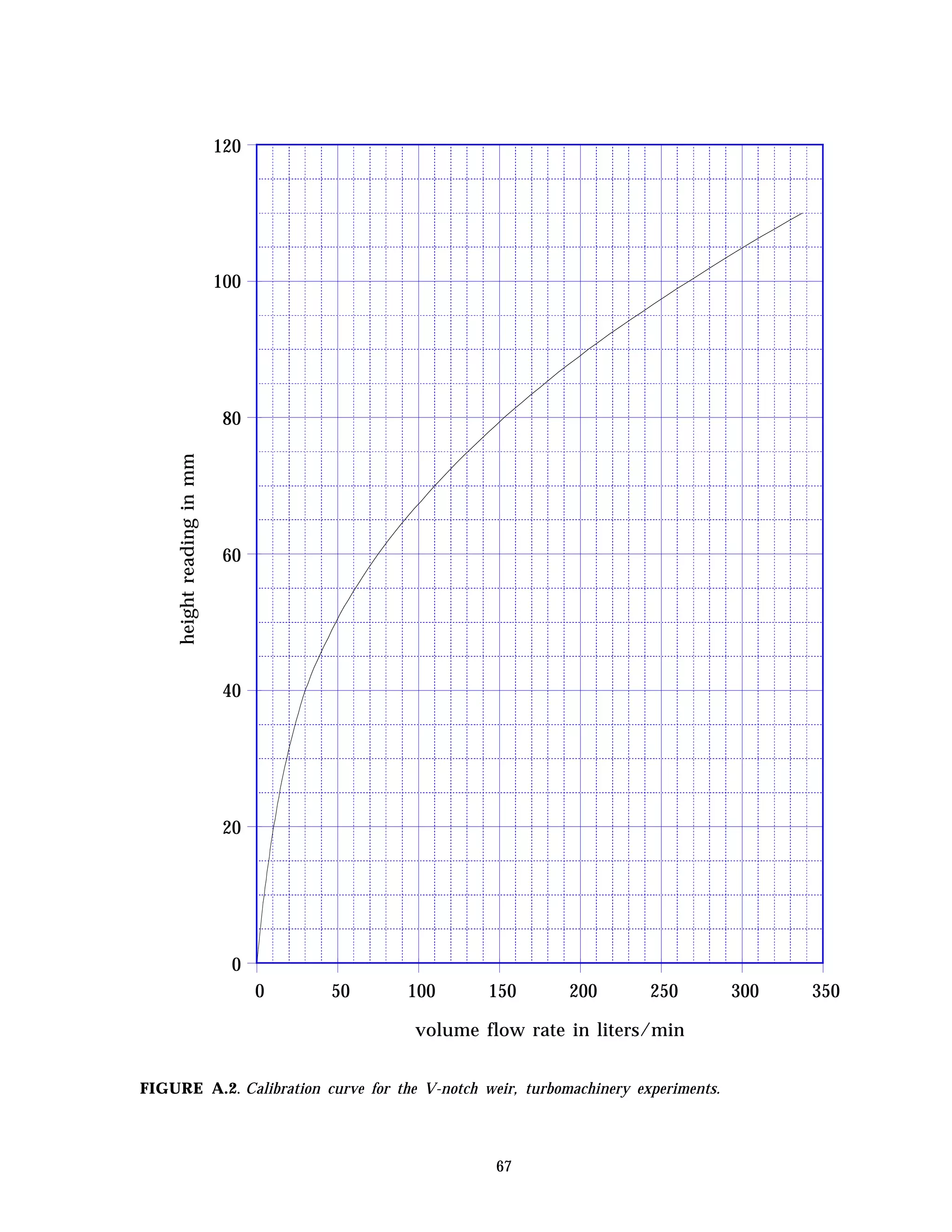
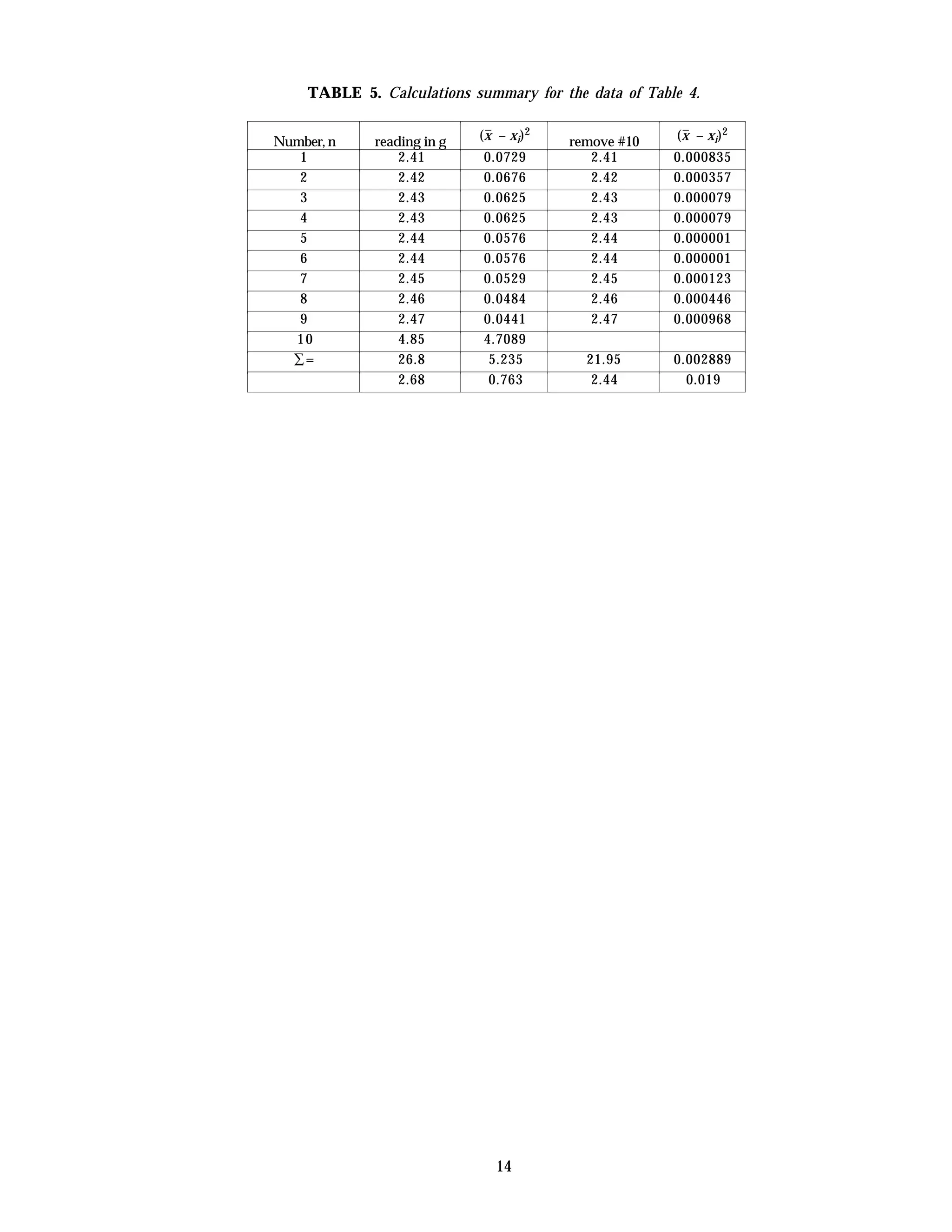
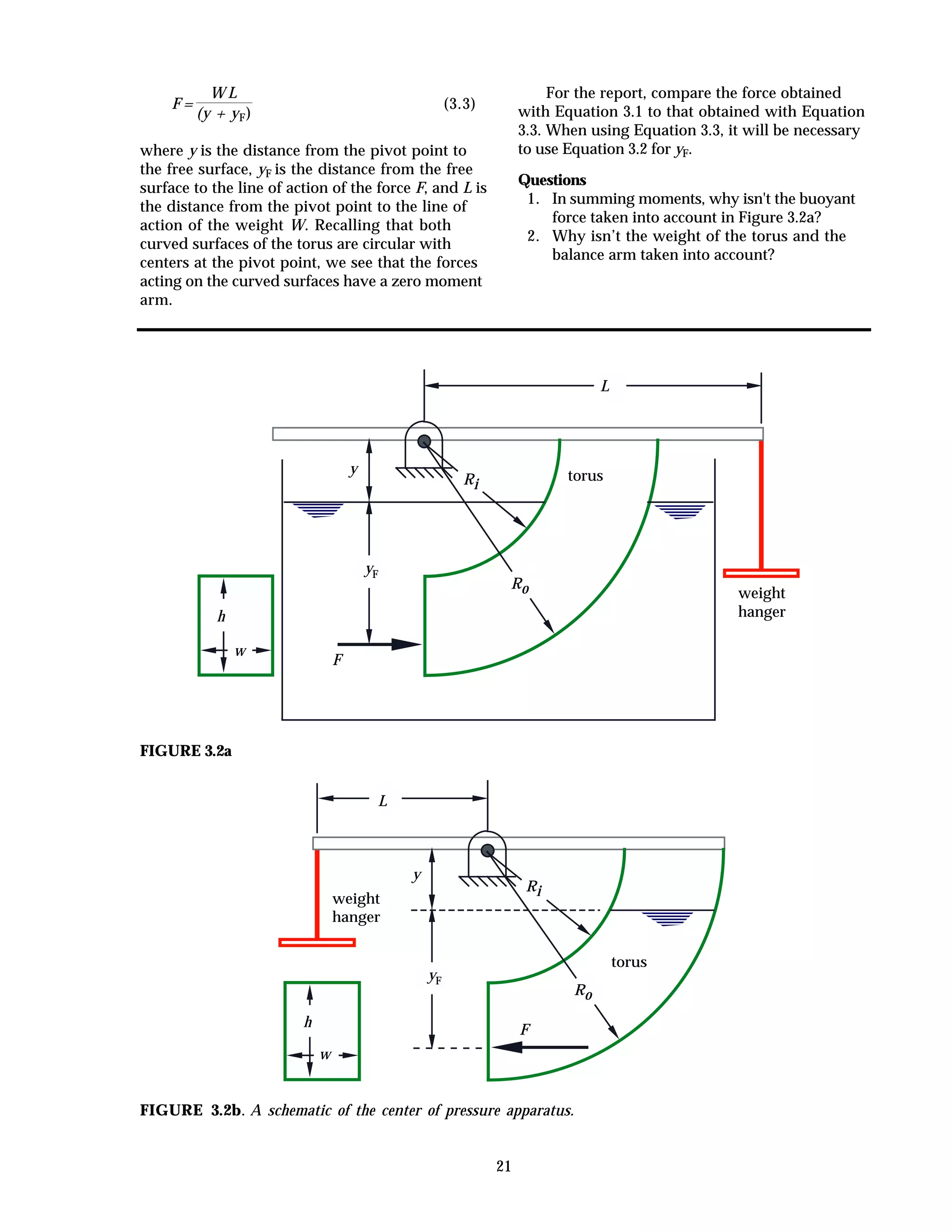
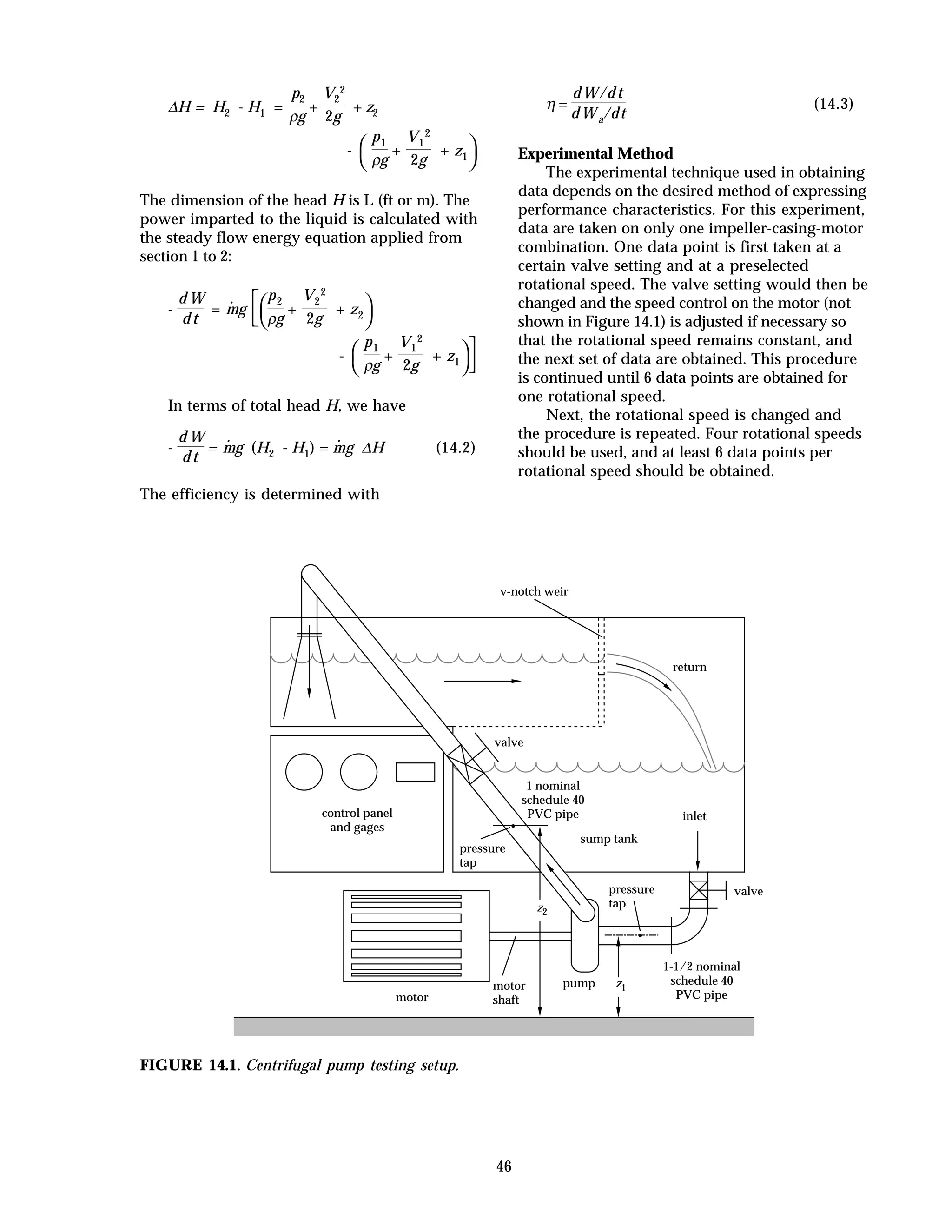
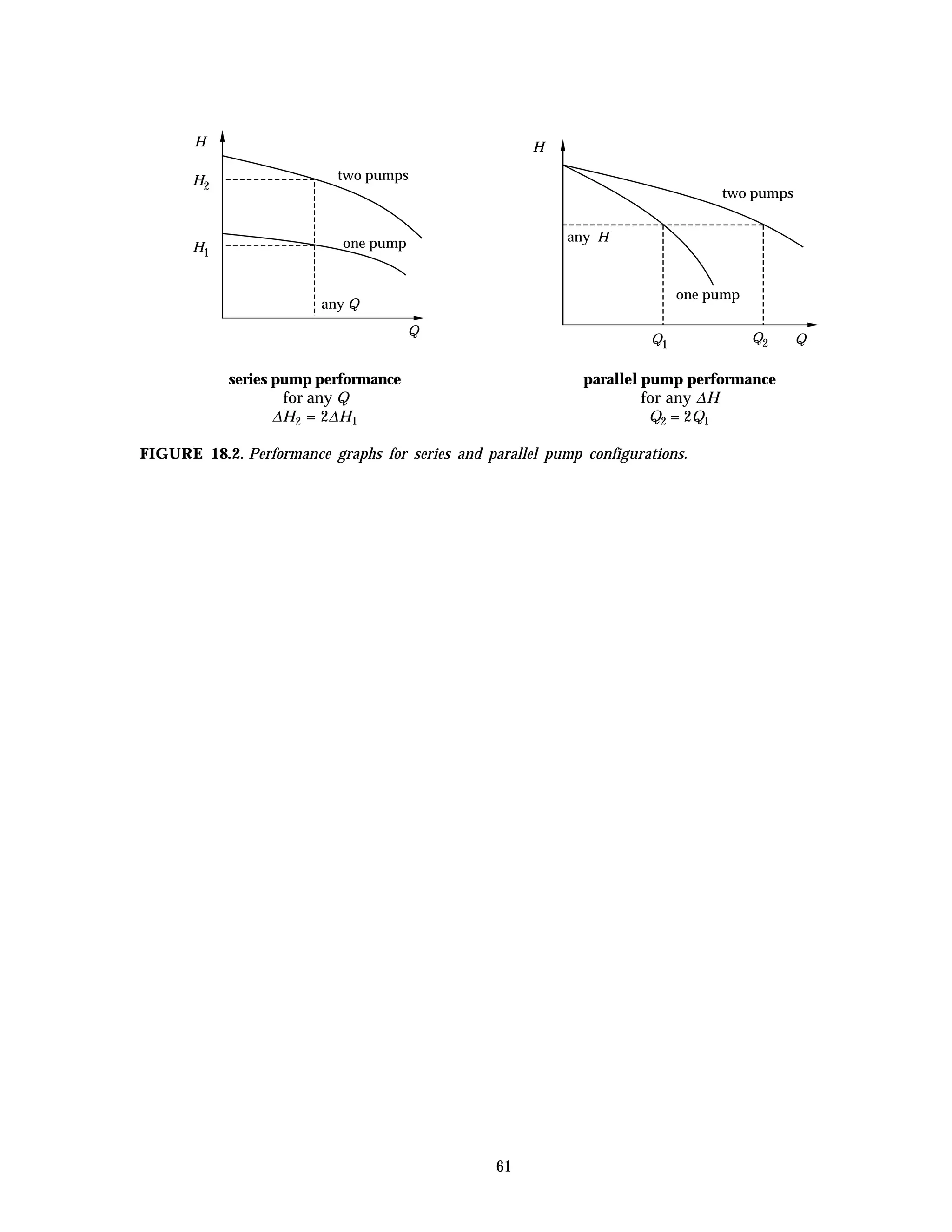
This document provides instructions and guidelines for conducting experiments in a fluid mechanics laboratory. It begins with an overview of course learning outcomes, safety procedures, and expectations for cleaning the lab space. It then discusses proper experimental methodology, including defining hypotheses, designing experiments to test hypotheses, collecting accurate and precise measurements, and analyzing results. The document emphasizes minimizing errors and uncertainties in measurements. It provides definitions for key terms like error, uncertainty, accuracy, and precision when evaluating experimental data. Finally, it outlines the content and procedures for 20 specific fluid mechanics experiments that will be conducted.

1. A Manual for the
MECHANICS
of
FLUIDS LABORATORY
removable glass cover
dye reservoir
valve
manifold with injectors
dye water flow
water inlet
to drain
plan
view
profile
view
grid on surface
beneath glass
manifold with injectors
grid on surface
beneath glass
circular
disk
circular
disk
William S. Janna
Department of Mechanical Engineering
The University of Memphis

2. 2
©2012 William S. Janna
All Rights Reserved.
No part of this manual may be reproduced, stored in a retrieval
system, or transcribed in any form or by any means—electronic, magnetic,
mechanical, photocopying, recording, or otherwise—
without the prior written consent of William S. Janna.

3. 3
TABLE OF CONTENTS
Item Page
Course Learning Outcomes, Cleanliness and Safety................................................4
Code of Student Conduct ...............................................................................................5
Statistical Treatment of Experimental.........................................................................6
Report Writing...............................................................................................................16
Experiment 1 Density and Surface Tension...................................................18
Experiment 2 Viscosity.......................................................................................20
Experiment 3 Center of Pressure on a Submerged Plane Surface.............21
Experiment 4 Impact of a Jet of Water ............................................................23
Experiment 5 Critical Reynolds Number in Pipe Flow...............................26
Experiment 6 Fluid Meters................................................................................28
Experiment 7 Pipe Flow .....................................................................................32
Experiment 8 Pressure Distribution About a Circular Cylinder................34
Experiment 9 Drag Force Determination .......................................................37
Experiment 10 Analysis of an Airfoil................................................................38
Experiment 11 Open Channel Flow—Sluice Gate .........................................40
Experiment 12 Open Channel Flow Over a Weir ..........................................42
Experiment 13 Open Channel Flow—Hydraulic Jump ................................44
Experiment 14 Measurement of Pump Performance....................................46
Experiment 15 Measurement of Velocity and Calibration of
a Meter for Compressible Flow.............................50
Experiment 16 Measurement of Fan Horsepower .........................................55
Experiment 17 External Laminar Flows Over Immersed Bodies................57
Experiment 18 Series-Parallel Pump Performance ........................................59
Experiment 19 Design of Experiments: Calibration of an Elbow Meter.....63
Experiment 20 Design of Experiments: Measurement of Force on a
Conical Object ...........................................................65
Appendix .........................................................................................................................67

4. 4
Course Learning Outcomes
The Fluid Mechanics Laboratory experiments are
set up so that experiments can be performed to
complement the theoretical information taught
in the fluid mechanics lecture course. Thus topical
areas have been identified and labeled as Course
Learning Outcomes (CLOs). The CLOs in the
MECH 3335 Laboratory are as follows:
TABLE 1. Course Learning Outcomes
1. Identify safe operating practices and
requirements for laboratory experiments
2. Measure fluid properties
3. Measure hydrostatic forces on a submerged
body
4. Use flow meters to measure flow rate in a
pipe
5. Measure pressure loss due to friction for pipe
flow
6. Measure drag/lift forces on objects in a flow,
or measure flow rate over a weir
7. Design and conduct an experiment, as well as
analyze and interpret data
8. Function effectively as a member of a team
Cleanliness
There are “housekeeping” rules that the user
of the laboratory should be aware of and abide
by. Equipment in the lab is delicate and each
piece is used extensively for 2 or 3 weeks per
semester. During the remaining time, each
apparatus just sits there, literally collecting dust.
University housekeeping staff are not required to
clean and maintain the equipment. Instead, there
are college technicians who will work on the
equipment when it needs repair, and when they
are notified that a piece of equipment needs
attention. It is important, however, that the
equipment stay clean, so that dust will not
accumulate too heavily.
The Fluid Mechanics Laboratory contains
equipment that uses water or air as the working
fluid. In some cases, performing an experiment
will inevitably allow water to get on the
equipment and/or the floor. If no one cleaned up
their working area after performing an
experiment, the lab would not be a comfortable or
safe place to work in. No student appreciates
walking up to and working with a piece of
equipment that another student or group of
students has left in a mess.
Consequently, students are required to clean
up their area at the conclusion of the performance
of an experiment. Cleanup will include removal
of spilled water (or any liquid), and wiping the
table top on which the equipment is mounted (if
appropriate). The lab should always be as clean
or cleaner than it was when you entered. Cleaning
the lab is your responsibility as a user of the
equipment. This is an act of courtesy that students
who follow you will appreciate, and that you
will appreciate when you work with the
equipment.
Safety
The layout of the equipment and storage
cabinets in the Fluid Mechanics Lab involves
resolving a variety of conflicting problems. These
include traffic flow, emergency facilities,
environmental safeguards, exit door locations,
unused equipment stored in the lab, etc. The goal
is to implement safety requirements without
impeding egress, but still allowing adequate work
space and necessary informal communication
opportunities.
Distance between adjacent pieces of
equipment is determined by locations of water
supply valves, floor drains, electrical outlets,
and by the need to allow enough space around the
apparatus of interest. Immediate access to the
Safety Cabinet and the Fire Extinguisher is also
considered. We do not work with hazardous
materials and safety facilities such as showers,
eye wash fountains, spill kits, fire blankets, etc.,
are not necessary.
Safety Procedures. There are five exit doors in
this lab, two of which lead to other labs. One
exit has a double door and leads directly to the
hallway on the first floor of the Engineering
Building. Another exit is a single door that also
leads to the hallway. The fifth exit leads
directly outside to the parking lot. In case of fire,
the doors to the hallway should be closed, and
the lab should be exited to the parking lot.
There is a safety cabinet attached to the
wall of the lab adjacent to the double doors. In
case of personal injury, the appropriate item
should be taken from the supply cabinet and used
in the recommended fashion. If the injury is
serious enough to require professional medical
attention, the student(s) should contact the Civil
Engineering Department in EN 104, Extension
2746.
Every effort has been made to create a
positive, clean, safety conscious atmosphere.
Students are encouraged to handle equipment
safely and to be aware of, and avoid being
victims of, hazardous situations.

5. 5
THE CODE OF STUDENT CONDUCT
Taken from The University of Memphis
1998–1999 Student Handbook
Institution Policy Statement
The University of Memphis students are citizens
of the state, local, and national governments, and
of the academic community. They are, therefore,
expected to conduct themselves as law abiding
members of each community at all times.
Admission to the University carries with it
special privileges and imposes special
responsibilities apart from those rights and
duties enjoyed by non-students. In recognition of
this special relationship that exists between the
institution and the academic community which it
seeks to serve, the Tennessee Board of Regents
has, as a matter of public record, instructed “the
presidents of the universities and colleges under
its jurisdiction to take such action as may be
necessary to maintain campus conditions…and to
preserve the integrity of the institution and its
educational environment.”
The following regulations (known as the Code
of Student Conduct) have been developed by a
committee made up of faculty, students, and staff
utilizing input from all facets of the University
Community in order to provide a secure and
stimulating atmosphere in which individual and
academic pursuits may flourish. Students are,
however, subject to all national, state and local
laws and ordinances. If a student’s violation of
such laws or ordinances also adversely affects the
University’s pursuit of its educational objectives,
the University may enforce its own regulations
regardless of any proceeding instituted by other
authorities. Additionally, violations of any
section of the Code may subject a student to
disciplinary measures by the University whether
or not such conduct is simultaneously violative of
state, local or national laws.
The term “academic misconduct” includes, but
is not limited to, all acts of cheating and
plagiarism.
The term “cheating” includes, but is not limited
to:
a. use of any unauthorized assistance in taking
quizzes, tests, or examinations;
b. dependence upon the aid of sources beyond
those authorized by the instructor in writing
papers, preparing reports, solving problems,
or carrying out other assignments;
c. the acquisition, without permission, of tests
or other academic material before such
material is revealed or distributed by the
instructor;
d. the misrepresentation of papers, reports,
assignments or other materials as the product
of a student’s sole independent effort, for the
purpose of affecting the student’s grade,
credit, or status in the University;
e. failing to abide by the instructions of the
proctor concerning test-taking procedures;
examples include, but are not limited to,
talking, laughing, failure to take a seat
assignment, failing to adhere to starting and
stopping times, or other disruptive activity;
f. influencing, or attempting to influence, any
University official, faculty member,
graduate student or employee possessing
academic grading and/or evaluation
authority or responsibility for maintenance of
academic records, through the use of bribery,
threats, or any other means or coercion in
order to affect a student’s grade or
evaluation;
g. any forgery, alteration, unauthorized
possession, or misuse of University documents
pertaining to academic records, including, but
not limited to, late or retroactive change of
course application forms (otherwise known as
“drop slips”) and late or retroactive
withdrawal application forms. Alteration or
misuse of University documents pertaining to
academic records by means of computer
resources or other equipment is also included
within this definition of “cheating.”
The term “plagiarism” includes, but is not limited
to, the use, by paraphrase or direct quotation, of
the published or unpublished work of another
person without full or clear acknowledgment. It
also includes the unacknowledged use of
materials prepared by another person or agency
engaged in the selling of term papers or other
academic materials.
Course Policy
Academic misconduct (acts of cheating and of
plagiarism) will not be tolerated. The Student
Handbook is quite specific regarding the course of
action to be taken by an instructor in cases where
academic misconduct may be an issue.

6. 6
Statistical Treatment of Experimental Data
Introduction
This laboratory course concerns making
measurements in various fluid situations and
geometries, and relating results of those
measurements to derived equations. The objective
is to determine how well the derived equations
describe the physical phenomena we are
modeling. In doing so, we will need to make
physical measurements, and it is essential that
we learn how to practice good techniques in
making scientific observations and in obtaining
measurements. We are making quantitative
estimates of physical phenomena under
controlled conditions.
Measurements
There are certain primary desirable
characteristics involved when making these
physical measurements. We wish that our
measurements would be:
a ) Observer-independent,
b) Consistent, and
c) Quantitative
So when reporting a measurements, we will be
stating a number. Furthermore, we will have to
add a dimension because a physical value
without a unit has no significance. In reporting
measurements, a question arises as to how should
we report data; i.e., how many significant digits
should we include? Which physical quantity is
associated with the measurement, and how
precise should it or could it be? It is prudent to
scrutinize the claimed or implied accuracy of a
measurement.
Performing experiments
In the course of performing an experiment, we
first would develop a set of questions or a
hypothesis, or put forth the theory. We then
identify the system variables to be measured or
controlled. The apparatus would have to be
developed and the equipment set up in a
particular way. An experimental protocol, or
procedure, is established and data are taken.
Several features of this process are
important. We want accuracy in our
measurements, but increased accuracy generally
corresponds to an increase in cost. We want the
experiments to be reproducible, and we seek to
minimize errors. Of course we want to address all
safety issues and regulations.
After we run the experiment, and obtain data,
we would analyze the results, draw conclusions,
and report the results.
Comments on Performing Experiments
• Keep in mind the fundamental state of
questions or hypotheses.
• Make sure the experiment design will answer
the right questions.
• Use estimation as a reality check, but do not
let it affect objectivity.
• Consider all possible safety issues.
• Design for repeatability and the appropriate
level of accuracy.
Error & Uncertainty—Definitions
The fluid mechanics laboratory is designed to
provide the students with experiments that
verify the descriptive equations we derive to
model physical phenomena. The laboratory
experience involves making measurements of
depth, area, and flow rate among other things. In
the following paragraphs, we will examine our
measurement methods and define terms that
apply. These terms include error, uncertainty,
accuracy, and precision.
Error. The error E is the difference between a
TRUE value, x, and a MEASURED value, xi:
E x xi= − (1)
There is no error-free measurement. All
measurements contain some error. How error is
defined and used is important. The significance of
a measurement cannot be judged unless the
associated error has been reliably estimated. In
Equation 1, because the true value of x is unknown,
the error E is unknown as well. This is always the
case.
The best we can hope for is to obtain the
estimate of a likely error, which is called an
uncertainty. For multiple measurements of the
same quantity, a mean value, x, (also called a
nominal value) can be calculated. Hence, the
error becomes:
E x x= −
However, because x is unknown, E is still
unknown.

7. 7
Uncertainty. The uncertainty, ∆x, is an estimate
of E as a possible range of errors:
∆x E≈ (2)
For example, suppose we measure a velocity and
report the result as
V = 110 m/s ± 5 m/s
The value of ± 5 m/s is defined as the uncertainty.
Alternatively, suppose we report the results as
V = 110 m/s ± 4.5%
The value of ± 4.5% is defined as the relative
uncertainty. It is common to hear someone speak
of “experimental errors,” when the correct
terminology should be “uncertainty.” Both terms
are used in everyday language, but it should be
remembered that the uncertainty is defined as an
estimate of errors.
Accuracy. Accuracy is a measure (or an estimate)
of the maximum deviation of measured values, xi,
from the TRUE value, x:
accuracy estimate of x xi= −max (3)
Again, because the true value x is unknown, then
the value of the maximum deviation is unknown.
The accuracy, then, is only an estimate of the
worst error. It is usually expressed as a
percentage; e.g., “accurate to within 5%.”
Accuracy and Precision. As mentioned, accuracy is
a measure (or an estimate) of the maximum
deviation of measured values from the true value.
So a question like:
“Are the measured values accurate?”
can be reformulated as
“Are the measured values close to the true
value?”
Accuracy was defined in Equation 3 as
accuracy estimate of x xi= −max (3)
Precision, on the other hand, is a measure (or an
estimate) of the consistency (or repeatability).
Thus it is the maximum deviation of a reading
(measurement), xi, from its mean value, x :
precision estimate of x xi= −max
(4)
Note the difference between accuracy and
precision.
Regarding the definition of precision, there is
no true value identified, only the mean value (or
average) of a number of repeated measurements of
the same quantity. Precision is a characteristic of
the measurement. In everyday language we often
conclude that “accuracy” and “precision” are the
same, but in error analysis there is a difference.
So a question like:
“Are the measured values precise?”
can be reformulated as
“Are the measured values close to each
other?”
As an illustration of the concepts of accuracy and
precision, consider the dart board shown in the
accompanying figures. Let us assume that the blue
darts show the measurements taken, and that the
bullseye represents the value to be measured.
When all measurements are clustered about the
bullseye, then we have very accurate and,
therefore, precise results (Figure 1a).
When all measurements are clustered
together but not near the bullseye, then we have
very precise but not accurate results (Figure 1b).
When all measurements are not clustered
together and not near the bullseye, but their
nominal value or average is the bullseye, then we
have accurate (on average) but not precise results
(Figure 1c).
When all measurements are not clustered
together and not near the bullseye, and their
average is the not at the bullseye, then we have
neither accurate nor precise results (Figure 1d).
We conclude that accuracy refers to the
correctness of the measurements, while precision
refers to their consistency.
Classification of Errors
Random error. A random error is one that arises
from a random source. Suppose for example that a
measurement is made many thousands of times
using different instruments and/or observers
and/or samples. We would expect to have random
errors affecting the measurement in either
direction (±) roughly the same number of times.
Such errors can occur in any scenario:
• Electrical noise in a circuit generally produces
a voltage error that may be positive or
negative by a small amount.

8. 8
1
18
4
13
6
10
15
2
173
7
16
8
11
14
9
12
5
FIGURE 1a. Accurate and Precise
1
18
4
13
6
10
15
2
173
7
16
8
11
14
9
12
5
FIGURE 1b. Precise but not Accurate.
1
18
4
13
6
10
15
2
173
7
16
8
11
14
9
12
5
FIGURE 1c. Precise but not Accurate.
1
18
4
13
6
10
15
2
173
7
16
8
11
14
9
12
5
FIGURE 1d. Neither Precise nor Accurate.
• By counting the total number of pennies in a
large container, one may occasionally pick up
two and count only one (or vice versa).
The question arises as to how can we reduce
random errors? There are no random error free
measurements. So random errors cannot be
eliminated, but their magnitude can be reduced.
On average, random errors tend to cancel out.
Systematic Error. A systematic error is one that is
consistent; that is, it happens systematically.
Typically, human components of measurement
systems are often responsible for systematic
errors. For example, systematic errors are common
in reading of a pressure indicated by an inclined
manometer.
Consider an experiment involving dropping a
ball from a given height. We wish to measure the
time it takes for the ball to move from where it is
dropped to when it hits the ground. We might
repeat this experiment several times. However,
the person using the stopwatch may consistently
have a tendency to wait until the ball bounces
before the watch is stopped. As a result, the time
measurement might be systematically too long.
Systematic measurements can be anticipated
and/or measured, and then corrected. This can be
done even after the measurements are made.
The question arises as to how can we reduce
systematic errors? This can be done in several
ways:
1. Calibrate the instruments being used by
checking with a known standard. The
standard can be what is referred to as:
a) a primary standard obtained from the
“National Institute of standards and
technology” (NIST— formerly the National
Bureau of Standards); or
b) a secondary standard (with a higher
accuracy instrument); or
c) A known input source.
2. Make several measurements of a certain
quantity under varying test conditions, such
as different observers and/or samples and/or
instruments.
3. Check the apparatus.
4. Check the effects of external conditions
5. Check the coherence of results.
A repeatability test using the same instrument is
one way of gaining confidence, but a far more

9. 9
reliable way is to use an entirely different
method to measure the desired quantity.
Uncertainty Analysis
Determining Uncertainty. When we state a
measurement that we have taken, we should also
state an estimate of the error, or the uncertainty.
As a rule of thumb, we use a 95% relative
uncertainty, or stated otherwise, we use a 95%
confidence interval.
Suppose for example, that we report the
height of a desk to be 38 inches ± 1 inch. This
suggests that we are 95% sure that the desk is
between 37 and 39 inches tall.
When reporting relative uncertainty, we
generally restrict the result to having one or two
significant figures. When reporting uncertainty in
a measurement using units, we use the same
number of significant figures as the measured
value. Examples are shown in Table 1:
TABLE 1. Examples of relative and absolute
uncertainty.
Relative uncertainty Uncertainty in units
3.45 cm ± 8.5% 5.23 cm ± 0.143 cm
6.4 N ± 2.0% 2.5 m/s ± 0.082 m/s
2.3 psi ± 0.1900% 9.25 in ± 0.2 in
9.2 m/s ± 8.598% 3.2 N ± 0.1873 N
The previous tables shows uncertainty in
measurements, but to determine uncertainty is
usually difficult. However, because we are using
a 95% confidence interval, we can obtain an
estimage. The estimate of uncertainty depends on
the measurement type: single sample
measurements, measurements of dependent
variables, or multi variable measurements.
Single-sample measurements. Single-sample
measurements are those in which the
uncertainties cannot be reduced by repetition. As
long as the test conditions are the same (i.e., same
sample, same instrument and same observer), the
measurements (for fixed variables) are single-
sample measurements, regardless of how many
times the reading is repeated.
Single-sample uncertainty. It is often simple to
identify the uncertainty of an individual
measurement. It is necessary to consider the limit
of the “scale readability,” and the limit
associated with applying the measurement tool
to the case of interest.
Measurement Of Function Of More Than One
Independent Variables. In many cases, several
different quantities are measured in order to
calculate another quantity—a dependent
variable. For example, the measurement of the
surface area of a rectangle is calculated using
both its measured length and its measured width.
Such a situation involves a propagation of
uncertainties.
Consider some measuring device that has as
its smallest scale division δx. The smallest scale
division limits our ability to measure something
with any more accuracy than δx/2. The ruler of
Figure 2a, as an example, has 1/4 inch as its
smallest scale division. The diameter of the
circle is between 4 and 4 1/4 inches. So we would
correctly report that
D = 41/8 ± 1/8 in.
This is the correct reported measurement for
Figure 2a and Figure 2b, even though the circles
are of different diameters. We can “guesstimate”
the correct measurement, but we cannot report
something more accurately than our measuring
apparatus will display. This does not mean that
the two circles have the same diameter, merely
that we cannot measure the diameters with a
greater accuracy than the ruler we use will allow.
0 1 2 3 4 5 6
(a)
0 1 2 3 4 5 6
(b)
FIGURE 2. A ruler used to measure the diameter
of a circle.
The ruler depicted in the figure could be any
arbitrary instrument with finite resolution. The
uncertainty due to the resolution of any
instrument is one half of the smallest increment

10. 10
displayed. This is the most likely single sample
uncertainty. It is also the most optimistic because
reporting this values assumes that all other
sources of uncertainty have been removed.
Multi-Sample Measurements. Multi-sample
measurements involve a significant number of
data points collected from enough experiments so
that the reliability of the results can be assured
by a statistical analysis.
In other words, the measurement of a
significant number of data points of the same
quantity (for fixed system variables) under
varying test conditions (i.e., different samples
and/or different instruments) will allow the
uncertainties to be reduced by the sheer number of
observations.
Uncertainty In Measurement of a Function of
Independent Variables. The concern in this
measurement is in the propagation of
uncertainties. In most experiments, several
quantities are measured in order to calculate a
desired quantity. For example, to estimate the
gravitational constant by dropping a ball from a
known height, the approximate equation would
be:
g
L
t
=
2
2
(5)
Now suppose we measured: L = 50.00 ± 0.01 m and
t = 3.1 ± 0.5 s. Based on the equation, we have:
g
L
t
= =
×
=
2 2 50 00
3 1
10 42 2
2.
.
. m/s
We now wish to estimate the uncertainty ∆g in
our calculation of g. Obviously, the uncertainty
∆g will depend on the uncertainties in the
measurements of L and t. Let us examine the
“worst cases.” These may be calculated as:
gmin
.
.
.=
×
=
2 49 99
3 6
7 72
2m/s
and
gmax
.
.
.=
×
=
2 50 01
2 6
14 82
2m/s
The confidence interval around g then is:
7 7 14 82 2
. .m/s m/s≤ ≤g (6)
Now it is unlikely for all single-sample
uncertainties in a system to simultaneously be the
worst possible. Some average or “norm” of the
uncertainties must instead be used in estimating a
combined uncertainty for the calculation of g.
Uncertainty In Multi-Sample Measurements.
When a set of readings is taken in which the
values vary slightly from each other, the
experimenter is usually concerned with the mean
of all readings. If each reading is denoted by xi
and there are n readings, then the arithmetic
mean value is given by:
x
x
n
i
i
n
=
∑
=1
(7)
Deviation. The deviation of each reading is
defined by:
d x xi i= − (8)
The arithmetic mean deviation is defined as:
d
n
di
i
n
= ∑ =
=
1
0
1
Note that the arithmetic mean deviation is zero:
Standard Deviation. The standard deviation is
given by:
σ =
−∑
−
=
( )x x
n
i
i
n
2
1
1
(9)
Due to random errors, experimental data is
dispersed in what is referred to as a bell
distribution, known also as a Gaussian or Normal
Distribution, and depicted in Figure 3.
xi
f(xi )
FIGURE 3. Gaussian or Normal Distribution.
The Gaussian or Normal Distribution is what
we use to describe the distribution followed by
random errors. A graph of this distribution is

11. 11
often referred to as the “bell” curve as it looks
like the outline of a bell. The peak of the
distribution occurs at the mean of the random
variable, and the standard deviation is a common
measure for how “fat” this bell curve is. Equation
10 is called the Probability Density Function for
any continuous random variable x.
f x e
x x
( )
( )
=
− −
1
2
2
22
σ π
σ (10)
The mean and the standard deviation are all
the information necessary to completely describe
any normally-distributed random variable.
Integrating under the curve of Figure 3 over
various limits gives some interesting results.
• Integrating under the curve of the normal
distribution from negative to positive
infinity, the area is 1.0 (i.e., 100 %). Thus the
probability for a reading to fall in the range
of ±∞ is 100%.
• Integrating over a range within ± σ from the
mean value, the resulting value is 0.6826. The
probability for a reading to fall in the range
of ± σ is about 68%.
• Integrating over a range within ± 2σ from the
mean value, the resulting value is 0.954. The
probability for a reading to fall in the range
of ± 2σ is about 95%.
• Integrating over a range within ± 3σ from the
mean value, the resulting value is 0.997. The
probability for a reading to fall in the range
of ± 3σ is about 99%.
TABLE 2. Probability for Gaussian Distribution
(tabulated in any statistics book)
Probability ± value of the mean
50% 0.6754σ
68.3% σ
86.6% 1.5σ
95.4% 2σ
99.7% 3σ
Estimating Uncertainty. We can now use the
probability function to help in determining the
accuracy of data obtained in an experiment. We
use the uncertainty level of 95%, which means
that we have a 95% confidence interval. In other
words, if we state that the uncertainty is ∆x, we
suggest that we are 95% sure that any reading xi
will be within the range of ± ∆x of the mean.
Thus, the probability of a sample chosen at
random of being within the range ± 2σ of the
mean is about 95%. Uncertainty then is defined as
twice the standard deviation:
∆x ≈ 2σ
Example 1. The manufacturer of a particular
alloy claims a modulus of elasticity of 40 ± 2 kPa.
How is that to be interpreted?
Solution: The general rule of thumb is that ± 2
kPa would represent a 95% confidence interval.
That is, if we randomly select many samples of
this manufacturer’s alloy we should find that
95% of the samples meet the stated limit of 40 ± 2
kPa.
Now it is possible that we can find a sample
that has a modulus of elasticity of 37 kPa;
however, it means that it is very unlikely.
Example 2 If we assume that variations in the
product follow a normal distribution, and that
the modulus of elasticity is within the range 40 ±
2 kPa, then what is the standard deviation, σ?
Solution: The uncertainty ≈ 95% of confidence
interval ≈ 2σ. Thus
± 2 kPa = ± 2σ
So
σ = 1 kPa
Example 3. Assuming that the modulus of
elasticity is 40 ± 2 kPa, estimate the probability
of finding a sample from this population with a
modulus of elasticity less than or equal to 37 kPa.
Solution: With σ = 1 kPa, we are seeking the
value of the integral under the bell shaped curve,
over the range of -∞ to – 3σ. Thus, the probability
that the modulus of elasticity is less than 37 kPa
is:
P(E < 37 kPa) =
100 - 99.7
2
= 0.15%
Statistically Based Rejection of “Bad” Data–
Chauvenet’s Criterion
Occasionally, when a sample of n
measurements of a variable is obtained, there
may be one or more that appear to differ
markedly from the others. If some extraneous

12. 12
influence or mistake in experimental technique
can be identified, these “bad data” or “wild
points” can simply be discarded. More difficult is
the common situation in which no explanation is
readily available. In such situations, the
experimenter may be tempted to discard the
values on the basis that something must surely
have gone wrong. However, this temptation must
be resisted, since such data may be significant
either in terms of the phenomena being studied or
in detecting flaws in the experimental technique.
On the other hand, one does not want an erroneous
value to bias the results. In this case, a statistical
criterion must be used to identify points that can
be considered for rejection. There is no other
justifiable method to “throw away” data points.
One method that has gained wide acceptance
is Chauvenet’s criterion; this technique defines
an acceptable scatter, in a statistical sense,
around the mean value from a given sample of n
measurements. The criterion states that all data
points should be retained that fall within a band
around the mean that corresponds to a
probability of 1-1/(2n). In other words, data
points can be considered for rejection only if the
probability of obtaining their deviation from the
mean is less than 1/(2n). This is illustrated in
Figure 4.
xi
f(xi )
Probability
1 - 1/(2n)
Reject
data
Reject
data
FIGURE 4. Rejection of “bad” data.
The probability 1-1/(2n) for retention of data
distributed about the mean can be related to a
maximum deviation dmax away from the mean by
using a Gaussian probability table. For the given
probability, the non dimensional maximum
deviation τmax can be determined from the table,
where
τmax =
|(xi – –x )|max
sx
=
dmax
sx
and sx is the precision index of the sample.
All measurements that deviate from the
mean by more than dmax/sx can be rejected. A new
mean value and a new precision index can then be
calculated from the remaining measurements. No
further application of the criterion to the sample
is allowed.
Using Chauvenet’s criterion, we say that the
values xi which are outside of the range
x C± σ (11)
are clearly errors and should be discarded for the
analysis. Such values are called outliers. The
constant C may be obtained from Table 3. Note
that Chauvenet’s criterion may be applied only
once to a given sample of readings.
The methodology for identifying and
discarding outlier(s) is a follows:
1. After running an experiment, sort the
outcomes from lowest to highest value. The
suspect outliers will then be at the top and/or
the bottom of the list.
2. Calculate the mean value and the standard
deviation.
3. Using Chauvenet’s criterion, discard outliers.
4. Recalculate the mean value and the standard
deviation of the smaller sample and stop. Do
not repeat the process; Chauvenet’s criterion
may be applied only once.
TABLE 3. Constants to use in Chauvenet’s
criterion, Equation 11.
Number,
n
dmax
sx
= C
3 1.38
4 1.54
5 1.65
6 1.73
7 1.80
8 1.87
9 1.91
10 1.96
15 2.13
20 2.24
25 2.33
50 2.57
100 2.81
300 3.14
500 3.29
1,000 3.48
Example 4. Consider an experiment in which we
measure the mass of ten individual “identical”
objects. The scale readings (in grams) are as
shown in Table 4.

13. 13
By visual examination of the results, we
might conclude that the 4.85 g reading is too high
compared to the others, and so it represents an
error in the measurement. We might tend to
disregard it. However, what if the reading was
2.50 or 2.51 g? We use Chauvenet’s criterion to
determine if any of the readings can be discarded.
TABLE 4. Data obtained in a series of
experiments.
Number, n reading in g
1 2.41
2 2.42
3 2.43
4 2.43
5 2.44
6 2.44
7 2.45
8 2.46
9 2.47
10 4.85
We apply the methodology described earlier.
The results of the calculations are shown in Table
5:
1. Values in the table are already sorted.
Column 1 shows the reading number, and
there are 10 readings of mass, as indicated in
column 2.
2. We calculate the mean and standard
deviation. The data in column 2 are added to
obtain a total of 26.8. Dividing this value by
10 readings gives 2.68, which is the mean
value of all the readings:
m– = 2.68 g
In column 3, we show the square of the
difference between each reading and the
mean value. Thus in row 1, we calculate
(x– – x1)2 = (2.68 – 2.41)2 = 0.0729
We repeat this calculation for every data
point. We then add these to obtain the value
5.235 shown in the second to last row of
column 3. This value is then divided by (n –1)
= 9 data points, and the square root is taken.
The result is 0.763, which is the standard
deviation, as defined earlier in Equation 9:
σ =
−∑
−
=
( )x x
n
i
i
n
2
1
1
= 0.763 (9)
3. Next, we apply Chauvenet’s criterion; for 10
data points, n = 10 and Table 3 reads C = 1.96.
We calculate Cσ = 1.96(0.763) = 1.50. The
range of “acceptable” values then is 2.68 ±
1.50, or:
m– – Cσ ≤ mi ≤ m– + Cσ
1.18 g ≤ m– ≤ 4.18 g
Any values outside the range of 1.18 and 4.18
are outliers and should be discarded.
4. Thus for the data of the example, the 4.85
value is an outlier and may be discarded. All
other points are valid. The last two columns
show the results of calculations made
without data point #10. The mean becomes
2.44, and the standard deviation is 0.019
(compare to 2.68, and 0.763, respectively).

14. 14
TABLE 5. Calculations summary for the data of Table 4.
Number, n reading in g (x– – xi)2
remove #10 (x– – xi)2
1 2.41 0.0729 2.41 0.000835
2 2.42 0.0676 2.42 0.000357
3 2.43 0.0625 2.43 0.000079
4 2.43 0.0625 2.43 0.000079
5 2.44 0.0576 2.44 0.000001
6 2.44 0.0576 2.44 0.000001
7 2.45 0.0529 2.45 0.000123
8 2.46 0.0484 2.46 0.000446
9 2.47 0.0441 2.47 0.000968
10 4.85 4.7089
∑= 26.8 5.235 21.95 0.002889
2.68 0.763 2.44 0.019
f(∂T,∂x

15. 16
REPORT WRITING
All reports in the Fluid Mechanics
Laboratory require a formal laboratory report
unless specified otherwise. The report should be
written in such a way that anyone can duplicate
the performed experiment and find the same
results as the originator. The reports should be
simple and clearly written. Reports are due one
week after the experiment was performed, unless
specified otherwise.
The report should communicate several ideas
to the reader. First the report should be neatly
done. The experimenter is in effect trying to
convince the reader that the experiment was
performed in a straightforward manner with
great care and with full attention to detail. A
poorly written report might instead lead the
reader to think that just as little care went into
performing the experiment. Second, the report
should be well organized. The reader should be
able to easily follow each step discussed in the
text. Third, the report should contain accurate
results. This will require checking and rechecking
the calculations until accuracy can be guaranteed.
Fourth, the report should be free of spelling and
grammatical errors. The following format, shown
in Figure R.1, is to be used for formal Laboratory
Reports:
Title Page–The title page should show the title
and number of the experiment, the date the
experiment was performed, experimenter's
name and experimenter's partners' names, all
spelled correctly.
Table of Contents –Each page of the report must
be numbered for this section.
Object –The object is a clear concise statement
explaining the purpose of the experiment.
This is one of the most important parts of the
laboratory report because everything
included in the report must somehow relate to
the stated object. The object can be as short as
one sentence.
Theory –The theory section should contain a
complete analytical development of all
important equations pertinent to the
experiment, and how these equations are used
in the reduction of data. The theory section
should be written textbook-style.
Procedure – The procedure section should contain
a schematic drawing of the experimental
setup including all equipment used in a parts
list with manufacturer serial numbers, if any.
Show the function of each part when
necessary for clarity. Outline exactly step-
Bibliography
Calibration Curves
Original Data Sheet
(Sample Calculation)
Appendix
Title Page
Discussion & Conclusion
(Interpretation)
Results (Tables
and Graphs)
Procedure (Drawings
and Instructions)
Theory
(Textbook Style)
Object
(Past Tense)
Table of Contents
Each page numbered
Experiment Number
Experiment Title
Your Name
Due Date
Partners’ Names
FIGURE R.1. Format for formal reports.
by-step how the experiment was performed in
case someone desires to duplicate it. If it
cannot be duplicated, the experiment shows
nothing.
Results – The results section should contain a
formal analysis of the data with tables,
graphs, etc. Any presentation of data which
serves the purpose of clearly showing the
outcome of the experiment is sufficient.
Discussion and Conclusion – This section should
give an interpretation of the results
explaining how the object of the experiment
was accomplished. If any analytical
expression is to be verified, calculate % error†
and account for the sources. Discuss this
†% error–An analysis expressing how favorably the
empirical data approximate theoretical information.
There are many ways to find % error, but one method is
introduced here for consistency. Take the difference
between the empirical and theoretical results and divide
by the theoretical result. Multiplying by 100% gives the
% error. You may compose your own error analysis as
long as your method is clearly defined.

16. 16
experiment with respect to its faults as well
as its strong points. Suggest extensions of the
experiment and improvements. Also
recommend any changes necessary to better
accomplish the object.
Each experiment write-up contains a
number of questions. These are to be answered
or discussed in the Discussion and Conclusions
section.
Appendix
(1) Original data sheet.
(2) Show how data were used by a sample
calculation.
(3) Calibration curves of instrument which
were used in the performance of the
experiment. Include manufacturer of the
instrument, model and serial numbers.
Calibration curves will usually be supplied
by the instructor.
(4) Bibliography listing all references used.
Short Form Report Format
Often the experiment requires not a formal
report but an informal report. An informal report
includes the Title Page, Object, Procedure,
Results, and Conclusions. Other portions may be
added at the discretion of the instructor or the
writer. Another alternative report form consists
of a Title Page, an Introduction (made up of
shortened versions of Object, Theory, and
Procedure) Results, and Conclusion and
Discussion. This form might be used when a
detailed theory section would be too long.
Graphs
In many instances, it is necessary to compose a
plot in order to graphically present the results.
Graphs must be drawn neatly following a specific
format. Figure R.2 shows an acceptable graph
prepared using a computer. There are many
computer programs that have graphing
capabilities. Nevertheless an acceptably drawn
graph has several features of note. These features
are summarized next to Figure R.2.
FEATURES OF NOTE
• Border is drawn about the entire graph.
• Axis labels defined with symbols and
units.
• Grid drawn using major axis divisions.
• Each line is identified using a legend.
• Data points are identified with a
symbol: “ ´” on the Qac line to denote
data points obtained by experiment.
• The line representing the theoretical
results has no data points represented.
• Nothing is drawn freehand.
• Title is descriptive, rather than
something like Q vs ∆h.
0
0.05
0.1
0.15
0.2
0 0.2 0.4 0.6 0.8 1
Q
th
Q
ac
Q
∆ hhead loss in m
flowrateinm
3
/s
FIGURE R.2. Theoretical and actual volume flow rate
through a venturi meter as a function of head loss.

17. 17
EXPERIMENT 1
FLUID PROPERTIES: DENSITY AND SURFACE TENSION
There are several properties simple
Newtonian fluids have. They are basic
properties which cannot be calculated for every
fluid, and therefore they must be measured.
These properties are important in making
calculations regarding fluid systems. Measuring
fluid properties, density and surface tension, is
the object of this experiment.
Part I: Density Measurement.
Equipment
Graduated cylinder or beaker
Liquid whose properties are to be
measured
Hydrometer cylinder
Scale
Method 1. The density of the test fluid is to be
found by weighing a known volume of the liquid
using the graduated cylinder or beaker and the
scale. The beaker is weighed empty. The beaker
is then filled to a certain volume according to the
graduations on it and weighed again. The
difference in weight divided by the volume gives
the weight per unit volume of the liquid. By
appropriate conversion, the liquid density is
calculated. The mass per unit volume, or the
density, is thus measured in a direct way.
Method 2. A second method of finding density
involves measuring buoyant force exerted on a
submerged object. The difference between the
weight of an object in air and the weight of the
object in liquid is known as the buoyant force (see
Figure 1.1).
W1
W2
FIGURE 1.1. Measuring the buoyant force on an
object with a hanging weight.
Referring to Figure 1.1, the buoyant force B is
found as
B = W1 - W2
The buoyant force is equal to the difference
between the weight of the object in air and the
weight of the object while submerged. Dividing
this difference by the volume displaced gives the
weight per unit volume from which density can be
calculated.
Method 3. A third method of making a density
measurement involves the use of a calibrated
hydrometer cylinder. The cylinder is submerged
in the liquid and the density is read directly on
the calibrated portion of the cylinder itself.
Experiment
Measure density using the methods assigned by
the instructor. Compare results of all
measurements.
Questions
1. Are the results of all the density
measurements in agreement?
2. How does the buoyant force vary with
depth of the submerged object? Why?
3. In your opinion, which method yielded the
“most accurate” results?
4. Are the results precise?
5. What is the mean of the values you
obtained?
6. What is the standard deviation of the
results?
7. Using Chauvenent’s rule, can any of the
measurements be discarded?

18. 18
Part II: Surface Tension Measurement
Equipment
Surface tension meter
Beaker
Test fluid
Surface tension is defined as the energy
required to pull molecules of liquid from beneath
the surface to the surface to form a new area. It is
therefore an energy per unit area (F⋅L/L2 = F/L).
A surface tension meter is used to measure this
energy per unit area and give its value directly. A
schematic of the surface tension meter is given in
Figure 1.2.
The platinum-iridium ring is attached to a
balance rod (lever arm) which in turn is attached
to a stainless steel torsion wire. One end of this
wire is fixed and the other is rotated. As the wire
is placed under torsion, the rod lifts the ring
slowly out of the liquid. The proper technique is
to lower the test fluid container as the ring is
lifted so that the ring remains horizontal. The
force required to break the ring free from the
liquid surface is related to the surface tension of
the liquid. As the ring breaks free, the gage at
the front of the meter reads directly in the units
indicated (dynes/cm) for the given ring. This
reading is called the apparent surface tension and
must be corrected for the ring used in order to
obtain the actual surface tension for the liquid.
The correction factor F can be calculated with the
following equation
F = 0.725 + √0.000 403 3(σa/ρ) + 0.045 34 - 1.679(r/R)
where F is the correction factor, σa is the
apparent surface tension read from the dial
(dyne/cm), ρ is the density of the liquid (g/cm3),
and (r/R) for the ring is found on the ring
container. The actual surface tension for the
liquid is given by
σ = Fσa
Experiment
Measure the surface tension of the liquid
assigned. Each member of your group should make
a measurement to become familiar with the
apparatus. Are all measurements in agreement?
FIGURE 1.2. A schematic of the
surface tension meter.
torsion wire
test liquid
platinum
iridium ring
clamp
balance rod

19. 19
EXPERIMENT 2
FLUID PROPERTIES: VISCOSITY
One of the properties of homogeneous liquids
is their resistance to motion. A measure of this
resistance is known as viscosity. It can be
measured in different, standardized methods or
tests. In this experiment, viscosity will be
measured with a falling sphere viscometer.
The Falling Sphere Viscometer
When an object falls through a fluid medium,
the object reaches a constant final speed or
terminal velocity. If this terminal velocity is
sufficiently low, then the various forces acting on
the object can be described with exact expressions.
The forces acting on a sphere, for example, that is
falling at terminal velocity through a liquid are:
Weight - Buoyancy - Drag = 0
ρsg
4
3
πR3 - ρg
4
3
πR3 - 6πµVR = 0
where ρs and ρ are density of the sphere and
liquid respectively, V is the sphere’s terminal
velocity, R is the radius of the sphere and µ is
the viscosity of the liquid. In solving the
preceding equation, the viscosity of the liquid can
be determined. The above expression for drag is
valid only if the following equation is valid:
ρVD
µ
< 1
where D is the sphere diameter. Once the
viscosity of the liquid is found, the above ratio
should be calculated to be certain that the
mathematical model gives an accurate
description of a sphere falling through the
liquid.
Equipment
Cylinder filled with test liquid
Scale
Stopwatch
Several small spheres with weight and
diameter to be measured
Drop a sphere into the cylinder liquid and
record the time it takes for the sphere to fall a
certain measured distance. The distance divided
by the measured time gives the terminal velocity
of the sphere. Repeat the measurement and
average the results. With the terminal velocity
of this and of other spheres measured and known,
the absolute and kinematic viscosity of the liquid
can be calculated. The temperature of the test
liquid should also be recorded. Use at least three
different spheres. (Note that if the density of
the liquid is unknown, it can be obtained from any
group who has completed or is taking data on
Experiment 1.)
d
V
FIGURE 2.1. Terminal velocity measurement (V =
d/time).
Questions
1. Should the terminal velocity of two
different size spheres be the same?
2. Does a larger sphere have a higher
terminal velocity?
3. Should the viscosity found for two different
size spheres be the same? Why or why not?
4. What are the shortcomings of this method?
5. Why should temperature be recorded?
6. Can this method be used for gases?
7. Can this method be used for opaque liquids?
8. Can this method be used for something like
peanut butter, or grease or flour dough?
Why or why not?
9. Perform an error analysis for one of the data
points. That is, determine the error
associated with all the measurements, and
provide an error band about the mean value.

20. 20
EXPERIMENT 3
CENTER OF PRESSURE ON A SUBMERGED
PLANE SURFACE
Submerged surfaces are found in many
engineering applications. Dams, weirs and water
gates are familiar examples of submerged plane
surfaces. It is important to have a working
knowledge of the forces that act on submerged
surfaces.
A plane surface located beneath the surface
of a liquid is subjected to a pressure due to the
height of liquid above it, as shown in Figure 3.1.
Pressure increases linearly with increasing depth
resulting in a pressure distribution that acts on
the submerged surface. The analysis of this
situation involves determining a force which is
equivalent to the pressure, and finding the line of
action of this force.
F
yF
FIGURE 3.1. Pressure distribution on a submerged
plane surface and the equivalent force.
For this case, it can be shown that the
equivalent force is:
F = ρgycA (3.1)
in which ρ is the liquid density, yc is the distance
from the free surface of the liquid to the centroid
of the plane, and A is the area of the plane in
contact with liquid. Further, the location of this
force yF below the free surface is
yF =
Ix x
ycA
+ yc (3.2)
in which Ixx is the second area moment of the
plane about its centroid. The experimental
verification of these equations for force and
distance is the subject of this experiment.
Figure 3.2a is a sketch of an apparatus that
we use to illustrate the concepts behind this
experiment. The apparatus consists of one-fourth
of a torus, consisting of a solid piece of material.
The torus is attached to a lever arm, which is
free to rotate (within limits) about a pivot point.
The torus has inside and outside radii, Ri and Ro
respectively, and it is constructed such that the
center of these radii is at the pivot point of the
lever arm. The torus is now submerged in a liquid,
and there will exist an unbalanced force F that is
exerted on the plane of dimensions h x w. In order
to bring the torus and lever arm back to their
balanced position, a weight Wmust be added to
the weight hanger. The force and its line of
action can be found with Equations 3.1 and 3.2.
Consider next the apparatus sketched in
Figure 3.2b. It is quite similar to that in Figure
3.2a, in that it consists of a torus attached to a
lever arm. In this case, however, the torus is
hollow, and can be filled with liquid. If the
depth of the liquid is equal to that in Figure 3.2a,
(as measured from the bottom of the torus), then
the forces in both cases will be equal in magnitude
but opposite in direction. Moreover, the distance
from the free surface of the liquid to the line of
action of both forces will also be equal. Thus,
there is an equivalence between the two devices.
Center of Pressure Measurement
Equipment
Center of Pressure Apparatus
(Figure 3.2b)
Weights
The torus and balance arm are located on a pivot
rod. Note that the pivot point for the balance
arm is the point of contact between the rod and
the torus. Place the weight hanger on the
apparatus, and add water into the trim tank (not
shown in the figure) to bring the submerged plane
back to the vertical position.
Start by adding 20 g to the weight hanger.
Then pour water into the torus until the
submerged plan is brought back to the vertical
position. Record the weight and the liquid
depth. Repeat this procedure for 4 more weights.
(Remember to record the distance from the pivot
point to the free surface for each case.)
From the depth measurement, the equivalent
force and its location are calculated using
Equations 3.1 and 3.2. Summing moments about the
pivot allows for a comparison between the
theoretical and actual force exerted. Referring to
Figure 3.2b, we have

21. 21
F =
W L
(y + yF)
(3.3)
where y is the distance from the pivot point to
the free surface, yF is the distance from the free
surface to the line of action of the force F, and L is
the distance from the pivot point to the line of
action of the weight W. Recalling that both
curved surfaces of the torus are circular with
centers at the pivot point, we see that the forces
acting on the curved surfaces have a zero moment
arm.
For the report, compare the force obtained
with Equation 3.1 to that obtained with Equation
3.3. When using Equation 3.3, it will be necessary
to use Equation 3.2 for yF.
Questions
1. In summing moments, why isn't the buoyant
force taken into account in Figure 3.2a?
2. Why isn’t the weight of the torus and the
balance arm taken into account?
weight
hanger
L
Ri
F
y
h
w
yF
Ro
torus
FIGURE 3.2a
weight
hanger
L
F
y
h
w
yF
Ri
Ro
torus
FIGURE 3.2b. A schematic of the center of pressure apparatus.

22. 22
EXPERIMENT 4
IMPACT OF A JET OF WATER
A jet of fluid striking a stationary object
exerts a force on that object. This force can be
measured when the object is connected to a spring
balance or scale. The force can then be related to
the velocity of the jet of fluid and in turn to the
rate of flow. The force developed by a jet stream
of water is the subject of this experiment.
Impact of a Jet of Liquid
Equipment
Jet Impact Apparatus
Object plates
Figure 4.1 is a schematic of the device used in
this experiment. The device consists of a catch
basin within a sump tank. A pump moves water
from the sump tank to the impact apparatus,
after which the water drains to the catch basin.
The plug is used to allow water to accumulate in
the catch basin. On the side of the sump tank is a
sight glass (not shown in Figure 4.1) showing the
water depth in the catch basin.
When flow rate is to be measured, water is
allowed to accumulate in the catch basin, and a
stopwatch is used to measure the time required
for the water volume to reach a pre-determined
volume, using the sight glass as an indicator. In
other words, we use the stopwatch to measure the
time required for a certain volume of water to
accumulate in the catch basin.
The sump tank acts as a support for the table
top which supports the impact apparatus. As
shown in Figure 4.1, the impact apparatus
contains a nozzle that produces a high velocity
jet of water. The jet is aimed at an object (such as
a flat plate or hemisphere). The force exerted on
the plate causes the balance arm to which the
plate is attached to deflect. A weight is moved
on the arm until the arm balances. A summation
of moments about the pivot point of the arm
allows for calculating the force exerted by the jet.
Water is fed through the nozzle by means of
a pump. The nozzle emits the water in a jet
stream whose diameter is constant. After the
water strikes the object, the water is channeled to
the catch basin to obtain the volume flow rate.
The variables involved in this experiment
are listed and their measurements are described
below:
1. Volume rate of flow–measured with the
catch basin (to obtain volume) and a
stopwatch (to obtain time). The volume flow
rate is obtained by dividing volume by time:
Q = V/t.
2. Velocity of jet–obtained by dividing volume
flow rate by jet area: V = Q/A. The jet is
cylindrical in shape.
3. Resultant force—found experimentally by
summation of moments about the pivot point
of the balance arm. The theoretical resultant
force is found by use of an equation derived by
applying the momentum equation to a control
volume about the plate.
Impact Force Analysis
(Theoretical Force)
The total force exerted by the jet equals the
rate of momentum loss experienced by the jet after
it impacts the object. For a flat plate, the force
equation is:
F =
ρQ2
A
(flat plate)
For a hemisphere,
F =
2ρQ2
A
(hemisphere)
For a cone whose included half angle is α,
F =
ρQ2
A
(1 + cos α) (cone)
These equations are easily derivable from the
momentum equation applied to a control volume
about the object.

23. 23
flat plate
pivot
balancing weight lever arm with
flat plate attached
water
jet nozzle
drain
sump tank
flow control
valve
motorpump
plug
catch basin
FIGURE 4.1. A schematic of the jet impact apparatus.
Procedure
I. Figure 4.2 shows a sketch of the lever arm
in the impact experiment. The impact object
should be in place and the thumbscrew on
the spring should be used to zero the lever
arm. This is done without any water flow.
(Units of the scales in the figures are
arbitrary.)
II. The pump is now turned on and a water jet
hits the impact object, which will deflect
the lever arm causing it to rotate slightly
counterclockwise. The balancing weight is
moved from the zero position to the
position required to re-balance the lever
arm (in this case identified as “3” in Figure
4.3). The spring is left untouched. Only the
balancing weight is moved in order to re-
balance the lever arm.
III. During the time that the water jet impacts
the object, the time required to calculate
volume flow rate is measured.

24. 24
40 1 2 3 5
Fs
Fo
Fw
dw1
do
ds
O
FIGURE 4.2. Lever arm in zero position without
any water flow.
40 1 2 3 5
Fs
Fo
Fw
F
dw2
do
ds
O
water jet
FIGURE 4.3. Lever arm in zero position when the
water jet is on.
Nomenclature
SYMBOL FORCE DISTANCE
Fs spring force ds
Fw balancing weight dw
Fo impact object do
F exerted by water jet do
Analysis (Actual Force as Measured)
Summing moments about point O in Figure 4.2
gives the following equation for the lever arm:
Fsds + Fodo + Fwdw1 = 0 (4.1)
Summing moments about point O gives the
following equation for the lever arm in Figure 4.3:
Fsds + Fodo – Fdo + Fwdw2 = 0 (4.2)
Now we compare Equations 4.1 and 4.2. We can
identify parameters that appear in both
equations that are constants. These are Fsds and
Fodo. We rearrange Equation 4.1 to solve for the
sum of these force-distance products:
Fsds + Fodo = – Fwdw1 (4.3)
Likewise, Equation 4.2 gives
Fsds + Fodo = + Fdo – Fwdw2 (4.4)
Subtracting Equation 4.4 from 4.3, we get
0 = – Fwdw1 – Fdo + Fwdw2
The force we are seeking is that exerted by the
water jet F; rearranging gives
Fdo = – Fwdw1 + Fwdw2 = Fw(dw2 – dw1)
or
F =
Fw(dw2 – dw1)
do
(4.5)
Thus, the force exerted by the water equals the
weight of what we have called the balancing
weight times a ratio of distances. The distance
(dw2 – dw1) is just the difference in readings of the
position of the balancing weight. The distance do
is the distance from the pivot to the location of
the impact object.
For your report, derive the appropriate
equation for each object you are assigned to use.
Compose a graph with volume flow rate on the
horizontal axis, and on the vertical axis, plot the
actual and theoretical force. Use care in choosing
the increments for each axis.

25. 25
EXPERIMENT 5
CRITICAL REYNOLDS NUMBER IN PIPE FLOW
The Reynolds number is a dimensionless ratio
of inertia forces to viscous forces and is used in
identifying certain characteristics of fluid flow.
The Reynolds number is extremely important in
modeling pipe flow. It can be used to determine
the type of flow occurring: laminar or turbulent.
Under laminar conditions the velocity
distribution of the fluid within the pipe is
essentially parabolic and can be derived from the
equation of motion. When turbulent flow exists,
the velocity profile is “flatter” than in the
laminar case because the mixing effect which is
characteristic of turbulent flow helps to more
evenly distribute the kinetic energy of the fluid
over most of the cross section.
In most engineering texts, a Reynolds number
of 2 100 is usually accepted as the value at
transition; that is, the value of the Reynolds
number between laminar and turbulent flow
regimes. This is done for the sake of convenience.
In this experiment, however, we will see that
transition exists over a range of Reynolds numbers
and not at an individual point.
The Reynolds number that exists anywhere in
the transition region is called the critical
Reynolds number. Finding the critical Reynolds
number for the transition range that exists in pipe
flow is the subject of this experiment.
Critical Reynolds Number Measurement
Equipment
Critical Reynolds Number Determination
Apparatus
Figure 5.1 is a schematic of the apparatus
used in this experiment. The constant head tank
provides a controllable, constant flow through
the transparent tube. The flow valve in the tube
itself is an on/off valve, not used to control the
flow rate. Instead, the flow rate through the tube
is varied with the rotameter valve at A. The
head tank is filled with water and the overflow
tube maintains a constant head of water. The
liquid is then allowed to flow through one of the
transparent tubes at a very low flow rate. The
valve at B controls the flow of dye; it is opened
and dye is then injected into the pipe with the
water. The dye injector tube is not to be placed in
the pipe entrance as it could affect the results.
Establish laminar flow by starting with a very
low flow rate of water and of dye. The injected
dye will flow downstream in a threadlike
pattern for very low flow rates. Once steady state
is achieved, the rotameter valve is opened
slightly to increase the water flow rate. The
valve at B is opened further if necessary to allow
more dye to enter the tube. This procedure of
increasing flow rate of water and of dye (if
necessary) is repeated throughout the
experiment.
Establish laminar flow in one of the tubes.
Then slowly increase the flow rate and observe
what happens to the dye. Its pattern may
change, yet the flow might still appear to be
laminar. This is the beginning of transition.
Continue increasing the flow rate and again
observe the behavior of the dye. Eventually, the
dye will mix with the water in a way that will
be recognized as turbulent flow. This point is the
end of transition. Transition thus will exist over a
range of flow rates. Record the flow rates at key
points in the experiment. Also record the
temperature of the water.
The object of this procedure is to determine
the range of Reynolds numbers over which
transition occurs. Given the tube size, the
Reynolds number can be calculated with:
Re =
VD
ν
where V (= Q/A) is the average velocity of
liquid in the pipe, D is the hydraulic diameter of
the pipe, and ν is the kinematic viscosity of the
liquid.
The hydraulic diameter is calculated from
its definition:
D =
4 x Area
Wetted Perimeter
For a circular pipe flowing full, the hydraulic
diameter equals the inside diameter of the pipe.
For a square section, the hydraulic diameter will
equal the length of one side (show that this is
the case). The experiment is to be performed for
both round tubes and the square tube. With good
technique and great care, it is possible for the
transition Reynolds number to encompass the
traditionally accepted value of 2 100.

26. 26
Questions
1. Can a similar procedure be followed for
gases?
2. Is the Reynolds number obtained at
transition dependent on tube size or shape?
3. Can this method work for opaque liquids?
drilled partitions
dye reservoir
on/off valve
rotameter
A
to drain
inlet to
tank
overflow
to drain
B
transparent tube
FIGURE 5.1. The critical Reynolds number determination apparatus.

27. 27
EXPERIMENT 6
FLUID METERS IN INCOMPRESSIBLE FLOW
There are many different meters used in pipe
flow: the turbine type meter, the rotameter, the
orifice meter, the venturi meter, the elbow meter
and the nozzle meter are only a few. Each meter
works by its ability to alter a certain physical
characteristic of the flowing fluid and then
allows this alteration to be measured. The
measured alteration is then related to the flow
rate. A procedure of analyzing meters to
determine their useful features is the subject of
this experiment.
The Venturi Meter
The venturi meter is constructed as shown in
Figure 6.1. It contains a constriction known as the
throat. When fluid flows through the
constriction, it must experience an increase in
velocity over the upstream value. The velocity
increase is accompanied by a decrease in static
pressure at the throat. The difference between
upstream and throat static pressures is then
measured and related to the flow rate. The
greater the flow rate, the greater the pressure
drop ∆p. So the pressure difference ∆h (= ∆p/ρg)
can be found as a function of the flow rate.
1
2
h
FIGURE 6.1. A schematic of the Venturi meter.
Using the hydrostatic equation applied to
the air-over-liquid manometer of Figure 6.1, the
pressure drop and the head loss are related by
(after simplification):
p1 - p2
ρg
= ∆h
By combining the continuity equation,
Q = A1V1 = A2V2
with the Bernoulli equation,
p1
ρ
+
V1
2
2
=
p2
ρ
+
V2
2
2
and substituting from the hydrostatic equation, it
can be shown after simplification that the
volume flow rate through the venturi meter is
given by
Qth = A2
√
2g∆h
1 - (D2
4/D1
4)
(6.1)
The preceding equation represents the theoretical
volume flow rate through the venturi meter.
Notice that is was derived from the Bernoulli
equation which does not take frictional effects
into account.
In the venturi meter, there exists small
pressure losses due to viscous (or frictional)
effects. Thus for any pressure difference, the
actual flow rate will be somewhat less than the
theoretical value obtained with Equation 6.1
above. For any ∆h, it is possible to define a
coefficient of discharge Cv as
Cv =
Qac
Qth
For each and every measured actual flow rate
through the venturi meter, it is possible to
calculate a theoretical volume flow rate, a
Reynolds number, and a discharge coefficient.
The Reynolds number is given by
Re =
V2D2
ν
(6.2)
where V2 is the velocity at the throat of the
meter (= Qac/A2).
The Orifice Meter and
Nozzle-Type Meter
The orifice and nozzle-type meters consist of
a throttling device (an orifice plate or bushing,
respectively) placed into the flow. (See Figures
6.2 and 6.3). The throttling device creates a
measurable pressure difference from its upstream
to its downstream side. The measured pressure
difference is then related to the flow rate. Like
the venturi meter, the pressure difference varies
with flow rate. Applying Bernoulli’s equation to
points 1 and 2 of either meter (Figure 6.2 or Figure
6.3) yields the same theoretical equation as that
for the venturi meter, namely, Equation 6.1. For
any pressure difference, there will be two
associated flow rates for these meters: the
theoretical flow rate (Equation 6.1), and the

28. 28
actual flow rate (measured in the laboratory).
The ratio of actual to theoretical flow rate leads
to the definition of a discharge coefficient: Co for
the orifice meter and Cn for the nozzle.
1 2
h
FIGURE 6.2. Cross sectional view of the orifice
meter.
1 2
h
FIGURE 6.3. Cross sectional view of the nozzle-
type meter, and a typical nozzle.
For each and every measured actual flow
rate through the orifice or nozzle-type meters, it
is possible to calculate a theoretical volume flow
rate, a Reynolds number and a discharge
coefficient. The Reynolds number is given by
Equation 6.2.
The Turbine-Type Meter
The turbine-type flow meter consists of a
section of pipe into which a small “turbine” has
been placed. As the fluid travels through the
pipe, the turbine spins at an angular velocity
that is proportional to the flow rate. After a
certain number of revolutions, a magnetic pickup
sends an electrical pulse to a preamplifier which
in turn sends the pulse to a digital totalizer. The
totalizer totals the pulses and translates them
into a digital readout which gives the total
volume of liquid that travels through the pipe
and/or the instantaneous volume flow rate.
Figure 6.4 is a schematic of the turbine type flow
meter.
rotor supported
on bearings
(not shown)
turbine rotor
rotational speed
proportional to
flow rate
to receiver
flow
straighteners
FIGURE 6.4. A schematic of a turbine-type flow
meter.
The Rotameter (Variable Area Meter)
The variable area meter consists of a tapered
metering tube and a float which is free to move
inside. The tube is mounted vertically with the
inlet at the bottom. Fluid entering the bottom
raises the float until the forces of buoyancy, drag
and gravity are balanced. As the float rises the
annular flow area around the float increases.
Flow rate is indicated by the float position read
against the graduated scale which is etched on
the metering tube. The reading is made usually at
the widest part of the float. Figure 6.5 is a sketch
of a rotameter.
tapered, graduated
transparent tube
freely
suspended
float
inlet
outlet
FIGURE 6.5. A schematic of the rotameter and its
operation.
Rotameters are usually manufactured with
one of three types of graduated scales:
1. % of maximum flow–a factor to convert scale
reading to flow rate is given or determined for
the meter. A variety of fluids can be used
with the meter and the only variable

29. 29
encountered in using it is the scale factor. The
scale factor will vary from fluid to fluid.
2. Diameter-ratio type–the ratio of cross
sectional diameter of the tube to the
diameter of the float is etched at various
locations on the tube itself. Such a scale
requires a calibration curve to use the meter.
3. Direct reading–the scale reading shows the
actual flow rate for a specific fluid in the
units indicated on the meter itself. If this
type of meter is used for another kind of fluid,
then a scale factor must be applied to the
readings.
Experimental Procedure
Equipment
Fluid Meters Apparatus
Stopwatch
The fluid meters apparatus is shown
schematically in Figure 6.6. It consists of a
centrifugal pump, which draws water from a
sump tank, and delivers the water to the circuit
containing the flow meters. For nine valve
positions (the valve downstream of the pump),
record the pressure differences in each
manometer. For each valve position, measure the
actual flow rate by diverting the flow to the
volumetric measuring tank and recording the time
required to fill the tank to a predetermined
volume. Use the readings on the side of the tank
itself. For the rotameter, record the position of
the float and/or the reading of flow rate given
directly on the meter. For the turbine meter,
record the flow reading on the output device.
Note that the venturi meter has two
manometers attached to it. The “inner”
manometer is used to calibrate the meter; that is,
to obtain ∆h readings used in Equation 6.1. The
“outer” manometer is placed such that it reads
the overall pressure drop in the line due to the
presence of the meter and its attachment fittings.
We refer to this pressure loss as ∆H (distinctly
different from ∆h). This loss is also a function of
flow rate. The manometers on the turbine-type
and variable area meters also give the incurred
loss for each respective meter. Thus readings of
∆H vs Qac are obtainable. In order to use these
parameters to give dimensionless ratios, pressure
coefficient and Reynolds number are used. The
Reynolds number is given in Equation 6.2. The
pressure coefficient is defined as
Cp =
g∆H
V2/2
(6.3)
All velocities are based on actual flow rate and
pipe diameter.
The amount of work associated with the
laboratory report is great; therefore an informal
group report is required rather than individual
reports. The write-up should consist of an
Introduction (to include a procedure and a
derivation of Equation 6.1), a Discussion and
Conclusions section, and the following graphs:
1. On the same set of axes, plot Qac vs ∆h and
Qth vs ∆h with flow rate on the vertical
axis for the venturi meter.
2. On the same set of axes, plot Qac vs ∆h and
Qth vs ∆h with flow rate on the vertical
axis for the orifice meter.
3. Plot Qac vs Qth for the turbine type meter.
4. Plot Qac vs Qth for the rotameter.
5. Plot Cv vs Re on a log-log grid for the
venturi meter.
6. Plot Co vs Re on a log-log grid for the orifice
meter.
7. Plot ∆H vs Qac for all meters on the same set
of axes with flow rate on the vertical axis.
8. Plot Cp vs Re for all meters on the same set
of axes (log-log grid) with Cp vertical axis.
Questions
1. Referring to Figure 6.2, recall that
Bernoulli's equation was applied to points 1
and 2 where the pressure difference
measurement is made. The theoretical
equation, however, refers to the throat area
for point 2 (the orifice hole diameter)
which is not where the pressure
measurement was made. Explain this
discrepancy and how it is accounted for in
the equation formulation.
2. Which meter in your opinion is the best one
to use?
3. Which meter incurs the smallest pressure
loss? Is this necessarily the one that should
always be used?
4. Which is the most accurate meter?
5. What is the difference between precision
and accuracy?
Air Over Liquid Manometry
Each corresponding pair of pressure taps on
the apparatus is attached to an air over liquid
(water, in this case), inverted U-tube manometer.
Use of the manometers can lead to some
difficulties that may need attention.
Figure 6.7 is a sketch of one manometer. The
left and right limbs are attached to pressure taps,

30. 30
denoted as p1 and p2. Accordingly, when the
system is operated, the liquid will rise in each
limb and reach an equilibrium point. The pressure
difference will appear as a difference in height
of the water columns. That is, the pressure
difference is given by:
p1 – p2 = ρg∆h
where ρ is that of the liquid, and ∆h is read
directly on the manometer.
In some cases, the liquid levels are at places
beyond where we would like them to be. To
alleviate this problem, the air release valve
may be opened (slowly) to let air out or in. When
this occurs, the two levels will still have the
same ∆h reading, but located at a different place
on the manometer.
Sometimes, air bubbles will appear within
the liquid. The apparatus used has water with a
small amount of liquid soap dissolved to reduce
the surface tension of the water. However, if the
presence of bubbles persists, the pump should be
cycled on and off several times, and this should
solve the problem.
air
liquid
air release
valve
p1
p2
∆h
FIGURE 6.7. Air over liquid manometer.
orifice meter
venturi meter
manometer
valve
turbine-type meter
rotameter sump tank
volumetric
measuring
tank
return
pump
motor
FIGURE 6.6. A schematic of the Fluid Meters Apparatus. (Orifice and Venturi meters: upstream
diameter is 1.025 inches; throat diameter is 0.625 inches.)

31. 31
EXPERIMENT 7
PIPE FLOW
Experiments in pipe flow where the
presence of frictional forces must be taken into
account are useful aids in studying the behavior
of traveling fluids. Fluids are usually transported
through pipes from location to location by pumps.
The frictional losses within the pipes cause
pressure drops. These pressure drops must be
known to determine pump requirements. Thus a
study of pressure losses due to friction has a useful
application. The study of pressure losses in pipe
flow is the subject of this experiment.
Pipe Flow
Equipment
Pipe Flow Test Rig
Figure 7.1 is a schematic of the pipe flow test
rig. The rig contains a sump tank which is used as
a water reservoir from which one or two
centrifugal pumps discharge water to the pipe
circuit. The circuit itself consists of six different
diameter lines and a return line all made of PVC
pipe. The circuit contains ball valves for
directing and regulating the flow, and can be used
to make up various series and parallel piping
combinations. The circuit has provision for
measuring pressure loss through the use of static
pressure taps (manometer board and pressure taps
are not shown in the schematic).
The six lines are 1/2, 3/4, 1, 11/4, 11/2, and 2
inch schedule 80 pipe. The topmost line is a return
line, and it is made of 2 inch pipe as well. The
apparatus contains two flow meters. The 1/2 line
contains a flow meter which is used only for that
pipe. The other flow meter in the return line is for
all other flows through the system. Because the
circuit contains flow meters, the measured
pressure losses can be obtained as a function of
flow rate.
As functions of the flow rate, measure the
pressure losses in inches of water for whatever
combination of flows and minor losses specified by
the instructor
• The instructor will specify which of the
pressure loss measurements are to be taken.
• Open and close the appropriate valves on the
apparatus to obtain the desired flow path.
• Use the valve closest to the pump(s) on its
downstream side to vary the volume flow
rate.
• With the pump on, record the assigned
pressure drops and the actual volume flow
rate from the flow meter.
• Using the valve closest to the pump, change
the volume flow rate and again record the
pressure drops and the new flow rate.
• Repeat this procedure until 9 different
volume flow rates and corresponding pressure
drop data have been recorded.
With pressure loss data in terms of ∆h, the
friction factor can be calculated with
f =
2g∆h
V2(L/D)
It is customary to graph the friction factor as a
function of the Reynolds number:
Re =
VD
ν
The f vs Re graph, called a Moody Diagram, is
traditionally drawn on a log-log grid. The graph
also contains a third variable known as the
roughness coefficient ε/D. For this experiment
the roughness factor ε is that for smooth walled
tubing.
Where fittings are concerned, the loss
incurred by the fluid is expressed in terms of a loss
coefficient K. The loss coefficient for any fitting
can be calculated with
K =
∆ h
V2/2g
where ∆h is the pressure (or head) loss across the
fitting. Values of K as a function of the flow rate
are to be obtained in this experiment.
For the report, calculate friction factor f and
graph it as a function of Reynolds number Re for
the assigned pipe(s). Compare to a Moody
diagram. Also calculate the loss coefficient for
the fitting(s) assigned, and determine if the loss
coefficient K varies with flow rate or Reynolds
number. Compare your K values to published ones.

32. 32
flow meter
Q2
open ball valve
closed ball valve
union fitting
flow direction
pumps
Q1
Q2
1/2 nominal
3/4
1
1 1/4
1 1/2
2
FIGURE 7.1. Schematic of the pipe friction apparatus (not to scale).

33. 33
EXPERIMENT 8
PRESSURE DISTRIBUTION ABOUT A CIRCULAR CYLINDER
In many engineering applications, it may be
necessary to examine the phenomena occurring
when an object is inserted into a flow of fluid. The
wings of an airplane in flight, for example, may
be analyzed by considering the wings stationary
with air moving past them. Certain forces are
exerted on the wing by the flowing fluid that
tend to lift the wing (called the lift force) and to
push the wing in the direction of the flow (drag
force). Objects other than wings that are
symmetrical with respect to the fluid approach
direction, such as a circular cylinder, will
experience no lift, only drag.
Drag and lift forces are caused by the
pressure differences exerted on the stationary
object by the flowing fluid. Skin friction between
the fluid and the object contributes to the drag
force but in many cases can be neglected. The
measurement of the pressure distribution existing
around a stationary cylinder in an air stream to
find the drag force is the object of this
experiment.
Consider a circular cylinder immersed in a
uniform flow. The streamlines about the cylinder
are shown in Figure 8.1. The fluid exerts pressure
on the front half of the cylinder in an amount
that is greater than that exerted on the rear
half. The difference in pressure multiplied by the
projected frontal area of the cylinder gives the
drag force due to pressure (also known as form
drag). Because this drag is due primarily to a
pressure difference, measurement of the pressure
distribution about the cylinder allows for finding
the drag force experimentally. A typical pressure
distribution is given in Figure 8.2. Shown in
Figure 8.2a is the cylinder with lines and
arrowheads. The length of the line at any point
on the cylinder surface is proportional to the
pressure at that point. The direction of the
arrowhead indicates that the pressure at the
respective point is greater than the free stream
pressure (pointing toward the center of the
cylinder) or less than the free stream pressure
(pointing away). Note the existence of a
separation point and a separation region (or
wake). The pressure in the back flow region is
nearly the same as the pressure at the point of
separation. The general result is a net drag force
equal to the sum of the forces due to pressure
acting on the front half (+) and on the rear half (-
) of the cylinder. To find the drag force, it is
necessary to sum the components of pressure at
each point in the flow direction. Figure 8.2b is a
graph of the same data as that in Figure 8.2a
except that 8.2b is on a linear grid.
Freestream
Velocity V
Stagnation
Streamline Wake
FIGURE 8.1. Streamlines of flow about a circular
cylinder.
separation
point
separation
point
0 30 60 90 120 150 180
p
(a) Polar Coordinate Graph (b) Linear Graph
FIGURE 8.2. Pressure distribution around a circular cylinder placed in a uniform flow.

34. 34
Pressure Measurement
Equipment
A Wind Tunnel
A Right Circular Cylinder with Pressure
Taps
Figure 8.3 is a schematic of a wind tunnel. It
consists of a nozzle, a test section, a diffuser and a
fan. Flow enters the nozzle and passes through
flow straighteners and screens. The flow is
directed through a test section whose walls are
made of a transparent material, usually
Plexiglas or glass. An object is placed in the test
section for observation. Downstream of the test
section is the diffuser followed by the fan. In the
tunnel that is used in this experiment, the test
section is rectangular and the fan housing is
circular. Thus one function of the diffuser is to
gradually lead the flow from a rectangular
section to a circular one.
Figure 8.4 is a schematic of the side view of
the circular cylinder. The cylinder is placed in
the test section of the wind tunnel which is
operated at a preselected velocity. The pressure
tap labeled as #1 is placed at 0° directly facing
the approach flow. The pressure taps are
attached to a manometer board. Only the first 18
taps are connected because the expected profile is
symmetric about the 0° line. The manometers will
provide readings of pressure at 10° intervals
about half the cylinder. For two different
approach velocities, measure and record the
pressure distribution about the circular cylinder.
Plot the pressure distribution on polar coordinate
graph paper for both cases. Also graph pressure
difference (pressure at the point of interest minus
the free stream pressure) as a function of angle θ
on linear graph paper. Next, graph ∆p cosθ vs θ
(horizontal axis) on linear paper and determine
the area under the curve by any convenient
method (counting squares or a numerical
technique).
The drag force can be calculated by
integrating the flow-direction-component of each
pressure over the area of the cylinder:
Df = 2RL ∫
0
π
∆p cosθdθ
The above expression states that the drag force is
twice the cylinder radius (2R) times the cylinder
length (L) times the area under the curve of
∆p cosθ vs θ.
Drag data are usually expressed as drag
coefficient CD vs Reynolds number Re. The drag
coefficient is defined as
CD =
Df
ρV2A/2
The Reynolds number is
Re =
ρVD
µ
inlet flow
straighteners
nozzle
test section
diffuser fan
FIGURE 8.3. A schematic of the wind tunnel used in this experiment.

35. 35
where V is the free stream velocity (upstream of
the cylinder), A is the projected frontal area of
the cylinder (2RL), D is the cylinder diameter, ρ
is the air density and µ is the air viscosity.
Compare the results to those found in texts.
static pressure
taps attach to
manometers
60
0
30
90
120
150
180
FIGURE 8.4. Schematic of the experimental
apparatus used in this experiment.

36. 36
EXPERIMENT 9
DRAG FORCE DETERMINATION
An object placed in a uniform flow is acted
upon by various forces. The resultant of these
forces can be resolved into two force components,
parallel and perpendicular to the main flow
direction. The component acting parallel to the
flow is known as the drag force. It is a function of
a skin friction effect and an adverse pressure
gradient. The component perpendicular to the
flow direction is the lift force and is caused by a
pressure distribution which results in a lower
pressure acting over the top surface of the object
than at the bottom. If the object is symmetric
with respect to the flow direction, then the lift
force will be zero and only a drag force will exist.
Measurement of the drag force acting on an object
immersed in the uniform flow of a fluid is the
subject of this experiment.
Equipment
Subsonic Wind Tunnel
Objects
A description of a subsonic wind tunnel is
given in Experiment 8 and is shown schematically
in Figure 8.3. The fan at the end of the tunnel
draws in air at the inlet. An object is mounted on a
stand that is pre calibrated to read lift and drag
forces exerted by the fluid on the object. A
schematic of the test section is shown in Figure
9.1. The velocity of the flow at the test section is
also pre calibrated. The air velocity past the
object can be controlled by changing the rotational
speed of the fan. Thus air velocity, lift force and
drag force are read directly from the tunnel
instrumentation.
There are a number of objects that are
available for use in the wind tunnel. These
include a disk, a smooth surfaced sphere, a rough
surface sphere, a hemisphere facing upstream,
and a hemisphere facing downstream. For
whichever is assigned, measure drag on the object
as a function of velocity.
Data on drag vs velocity are usually graphed
in dimensionless terms. The drag force Df is
customarily expressed in terms of the drag
coefficient CD (a ratio of drag force to kinetic
energy):
CD =
Df
ρV2A/2
in which ρ is the fluid density, V is the free
stream velocity, and A is the projected frontal
area of the object. Traditionally, the drag
coefficient is graphed as a function of the
Reynolds number, which is defined as
Re =
VD
ν
where D is a characteristic length of the object
and ν is the kinematic viscosity of the fluid. For
each object assigned, graph drag coefficient vs
Reynolds number and compare your results to
those published in texts. Use log-log paper if
appropriate.
Questions
1. How does the mounting piece affect the
readings?
2. How do you plan to correct for its effect, if
necessary?
drag force
measurement
lift force
measurement
uniform flow mounting stand
object
FIGURE 9.1. Schematic of an object mounted in
the test section of the wind tunnel.

37. 37
EXPERIMENT 10
ANALYSIS OF AN AIRFOIL
A wing placed in the uniform flow of an
airstream will experience lift and drag forces.
Each of these forces is due to a pressure
difference. The lift force is due to the pressure
difference that exists between the lower and
upper surfaces. This phenomena is illustrated in
Figure 10.1. As indicated the airfoil is immersed
in a uniform flow. If pressure could be measured at
selected locations on the surface of the wing and
the results graphed, the profile in Figure 10.1
would result. Each pressure measurement is
represented by a line with an arrowhead. The
length of each line is proportional to the
magnitude of the pressure at the point. The
direction of the arrow (toward the horizontal
axis or away from it) represents whether the
pressure at the point is less than or greater than
the free stream pressure measured far upstream of
the wing.
stagnation
point
negative pressure
gradient on upper
surface
positive pressure
on lower surface
Cp
pressure
coefficient
stagnation
point
c
chord, c
FIGURE 10.1. Streamlines of flow about a wing
and the resultant pressure distribution.
Lift and Drag Measurements for a Wing
Equipment
Wind Tunnel (See Figure 8.3)
Wing with Pressure Taps
Wing for Attachment to Lift & Drag
Instruments (See Figure 10.2)
Experiment
For a number of wings, lift and drag data
vary only slightly with Reynolds number and
therefore if lift and drag coefficients are graphed
as a function of Reynolds number, the results are
not that meaningful. A more significant
representation of the results is given in what is
known as a polar diagram for the wing. A polar
diagram is a graph on a linear grid of lift
coefficient (vertical axis) as a function of drag
coefficient. Each data point on the graph
corresponds to a different angle of attack, all
measured at one velocity (Reynolds number).
Referring to Figure 10.2 (which is the
experimental setup here), the angle of attack α is
measured from a line parallel to the chord c to a
line that is parallel to the free stream velocity.
Obtain lift force, drag force and angle of
attack data using a pre selected velocity. Allow
the angle of attack to vary from a negative angle
to the stall point and beyond. Obtain data at no
less than 9 angles of attack. Use the data to
produce a polar diagram.
Analysis
Lift and drag data are usually expressed in
dimensionless terms using lift coefficient and drag
coefficient. The lift coefficient is defined as
CL =
Lf
ρV2A/2
where Lf is the lift force, ρ is the fluid density, V
is the free stream velocity far upstream of the
wing, and A is the area of the wing when seen
from a top view perpendicular to the chord
length c. The drag coefficient is defined as
CD =
Df
ρV2A/2
in which Df is the drag force.

38. 38
drag force
measurement
lift force
measurement
uniform flow mounting stand
c
drag
lift
FIGURE 10.2. Schematic of lift and drag measurement in a test section.

39. 39
EXPERIMENT 11
OPEN CHANNEL FLOW—SLUICE GATE
Liquid motion in a duct where a surface of the
fluid is exposed to the atmosphere is called open
channel flow. In the laboratory, open channel
flow experiments can be used to simulate flow in a
river, in a spillway, in a drainage canal or in a
sewer. Such modeled flows can include flow over
bumps or through dams, flow through a venturi
flume or under a partially raised gate (a sluice
gate). The last example, flow under a sluice gate,
is the subject of this experiment.
Flow Through a Sluice Gate
Equipment
Open Channel Flow Apparatus
Sluice Gate Model
Figure 11.1 is a sketch of the flow pattern
under a sluice gate. Upstream of the gate, the
velocity is V0, and the liquid height is h0. The
gate is a distance h1 above the bottom of the
channel, and downstream, the liquid height is
h2. The channel width is b.
The objective of this experiment is to make
measurements for a number of gate positions and
flow rates, and to determine whether the
equations we derive for a sluice gate are accurate
in their description of the resulting flows.
h0
h1
h2
V0
sluice
gate
FIGURE 11.1. Schematic of flow under a sluice
gate.
Theory
The continuity equation applied about the
sluice gate is
V0h0b = V2h2b (11.1)
Under real conditions, h2 is somewhat less than
h1. We therefore introduce a contraction
coefficient Cc defined as
Cc =
h2
h1
Substituting into Equation 11.1, canceling the
channel width b, and solving for V0, we get
V0 = V2
Cch1
h0
(11.2)
The Bernoulli Equation applied about the gate is
V0
2
2g
+ h0 =
V2
2
2g
+ h2 (11.3)
Substituting for V0 from Equation 11.2, we obtain
V2
2Cc
2h1
2/h0
2
2g
+ h0 =
V2
2
2g
+ Cch1
Rearranging and solving for V2, we have
V2 =



2g
h0 – Cch1
1 – Cc
2h1
2/h0
2
1/2
Factoring h0 and noting the relationship between
the numerator and denominator, the preceding
equation becomes
V2 =



2gh0
1 + Cch1/h0
1/2
(11.4)
The flow rate is the product of area and velocity.
At section 2, the flow rate may be written as
Q = V2h2b = V2Cch1b
Substituting from Equation 11.4 yields
Q = Cch1b



2gh0
1 + Cch1/h0
1/2
(11.5)
Introducing a discharge coefficient Cs, we write
Q = Csb √2gh0 (11.6)
Comparison with Equation 11.5 gives
Cs =
Cc
√1 + Cch1/h0
(11.7)

40. 40
We see that the contraction coefficient and the
discharge coefficient depend only on the
upstream height and the gate height.
Procedure
Set up the open channel flow apparatus
(Figure 11.2) to obtain flow under a sluice gate.
For nine (if possible) different flow rate/gate
position combinations, record upstream height,
gate height, downstream height, and volume
flow rate.
Calculations
Calculate the contraction coefficient, the
discharge coefficient (Equation 11.7), and the
expected volume flow rate (Equation 11.6).
Compare the calculated flow rate (theoretical)
with the measured (actual) value.
Include in Your Report
• Detailed derivation of the equations
• Graph of contraction coefficient as a function
of the ratio h1/h0
• Graph of discharge coefficient as a function of
the ratio h1/h0
• Graph of flow rates (actual and theoretical)
as a function of the ratio h1/h0
• Discussion of your results
sump tank
pump/motor
pump discharge
pipe
valve
head tank
sluice gate
turbine
meter
flow channel
FIGURE 11.2. Schematic of the open channel flow apparatus.

41. 41
EXPERIMENT 12
OPEN CHANNEL FLOW OVER A WEIR
Flow meters used in pipes introduce an
obstruction into the flow which results in a
measurable pressure drop that in turn is related to
the volume flow rate. In an open channel, flow
rate can be measured similarly by introducing an
obstruction into the flow. A simple obstruction,
called a weir, consists of a vertical plate
extending the entire width of the channel. The
plate may have an opening, usually rectangular,
trapezoidal, or triangular. Other configurations
exist and all are about equally effective. The use
of a weir to measure flow rate in an open channel
is the subject of this experiment.
Flow Over a Weir
Equipment
Open Channel Flow Apparatus (See
Figure 11.2)
Several Weirs
The open channel flow apparatus allows for
the insertion of a weir and measurement of liquid
depths. The channel is fed by two centrifugal
pumps. Each pump has a discharge line which
contains an turbine meter with digital readout,
which provide the means of determining the
actual flow rate into the channel.
Figure 12.1 is a sketch of the side and
upstream view of a 90 degree (included angle) V-
notch weir. Analysis of this weir is presented
here for illustrative purposes. Note that
upstream depth measurements are made from the
lowest point of the weir over which liquid flows.
This is the case for the analysis of all
conventional weirs. A coordinate system is
imposed whose origin is at the intersection of the
free surface and a vertical line extending upward
from the vertex of the V-notch. We select an
element that is dy thick and extends the entire
width of the flow cross section. The velocity of
the liquid through this element is found by
applying Bernoulli's equation:
pa
ρ
+
Vo
2
2
+ gh =
pa
ρ
+
V2
2
+ g(h - y)
Note that in pipe flow, pressure remained in the
equation when analyzing any of the differential
pressure meters (orifice or venturi meters). In open
channel flows, the pressure terms represents
atmospheric pressure and cancel from the
Bernoulli equation. The liquid height is
therefore the only measurement required here.
From the above equation, assuming Vo negligible:
V = √2gy (12.1)
Equation 12.1 is the starting point in the analysis
of all weirs. The incremental flow rate of liquid
through layer dy is:
dQ = 2Vxdy = √2gy(2x)dy
From the geometry of the V-notch and with
respect to the coordinate axes, we have y = h - x.
pa
pa
Vo
V
h
y
dy
x
x axis
y axis
FIGURE 12.1. Side and upstream views of a 90° V-notch weir.

42. 42
Therefore,
Q = ∫
0
h
(2√2g)y1/2(h - y)d y
Integration gives
Qth =
8
15
√2g h5/2 =Ch5/2 (12.2)
where C is a constant. The above equation
represents the ideal or theoretical flow rate of
liquid over the V-notch weir. The actual
discharge rate is somewhat less due to frictional
and other dissipative effects. As with pipe
meters, we introduce a discharge coefficient
defined as:
C' =
Qac
Qth
The equation that relates the actual volume flow
rate to the upstream height then is
Qac = C'Ch5/2
It is convenient to combine the effects of the
constant C and the coefficient C’ into a single
coefficient Cvn for the V-notch weir. Thus we
reformulate the previous two equations to obtain:
Cvn ≈
Qac
Qth
(12.3)
Qac = Cvnh5/2 (12.4)
Each type of weir will have its own coefficient.
Calibrate each of the weirs assigned by the
instructor for 7 different upstream height
measurements. Derive an appropriate equation
for each weir used (similar to Equation 12.4)
above. Determine the coefficient applicable for
each weir tested. List the assumptions made in
each derivation. Discuss the validity of each
assumption, pointing out where they break down.
Graph upstream height vs actual and theoretical
volume flow rates. Plot the coefficient of
discharge (as defined in Equation 12.3) as a
function of the upstream Froude number.
FIGURE 12.2. Other types of weirs–semicircular, contracted and suppressed, respectively.

43. 43
EXPERIMENT 13
OPEN CHANNEL FLOW—HYDRAULIC JUMP
When spillways or other similar open
channels are opened by the lifting of a gate,
liquid passing below the gate has a high velocity
and an associated high kinetic energy. Due to the
erosive properties of a high velocity fluid, it
may be desirable to convert the high kinetic
energy (e.g. high velocity) to a high potential
energy (e.g., a deeper stream). The problem then
becomes one of rapidly varying the liquid depth
over a short channel length. Rapidly varied flow
of this type produces what is known as a
hydraulic jump.
Consider a horizontal, rectangular open
channel of width b, in which a hydraulic jump
has developed. Figure 13.1 shows a side view of a
hydraulic jump. Figure 13.1 also shows the depth
of liquid upstream of the jump to be h1, and a
downstream depth of h2. Pressure distributions
upstream and downstream of the jump are drawn
in as well. Because the jump occurs over a very
short distance, frictional effects can be neglected.
A force balance would therefore include only
pressure forces. Applying the momentum equation
in the flow direction gives:
p1A1 - p2A2 = ρQ(V2 - V1)
Pressure in the above equation represents the
pressure that exists at the centroid of the cross
section. Thus p = ρg(h/2). With a rectangular
cross section of width b (A = bh), the above
equation becomes
h1g
2
(h1b) -
h2g
2
(h2b) = Q(V2 - V1)
From continuity, A1V1 = A2V2 = Q. Combining and
rearranging,
h1
2 - h2
2
2
=
Q 2
gb2




1
h2
-
1
h1
Simplifying,
h2
2 + h2h1 - 2
Q2
gb2h1
= 0
Solving for the downstream height yields one
physically (nonnegative) possible solution:
h2 = -
h1
2
+
√2Q 2
gb2h1
+
h1
2
4
from which the downstream height can be found.
By applying Bernoulli’s Equation along the free
surface, the energy lost irreversibly can be
calculated as
Lost Energy = E =
g(h2 - h1)3
4h2h1
and the rate of energy loss is
d W
d t
= ρQE
The above equations are adequate to properly
describe a hydraulic jump.
Hydraulic Jump Measurements
Equipment
Open Channel Flow Apparatus (Figure 11.2)
The channel can be used in either a
horizontal or a sloping configuration. The device
contains two pumps which discharge water
through calibrated turbine meters connected to
digital readouts. The device also contains on the
channel bottom two forward facing brass tubes.
Each tube is connected to a vertical Plexiglas
tube. The height of the water in either of these
tubes represents the energy level at the
respective tube location. The difference in height
is the actual lost energy (E) for the jump of
interest.
FIGURE 13.1. Schematic of a
hydraulic jump in an open
channel.
h1
V2
V1
p1
p2
h2

44. 44
Develop a hydraulic jump in the channel;
record upstream and downstream heights,
manometer readings (from which the actual
volume flow rate is obtained) and the lost energy
E. By varying the flow rate, upstream height,
downstream height and/or the channel slope,
record measurements on different jumps. Derive
the applicable equations in detail and substitute
appropriate values to verify the predicted
downstream height and lost energy. In other
words, the downstream height of each jump is to
be measured and compared to the downstream
height calculated with Equation 13.1. The same
is to be done for the rate of energy loss (Equation
13.2).
Analysis
Data on a hydraulic jump is usually specified
in two ways both of which will be required for
the report. Select any of the jumps you have
measurements for and construct a momentum
diagram . A momentum diagram is a graph of
liquid depth on the vertical axis vs momentum on
the horizontal axis, an example of which is
shown in Figure 13.2. As indicated in the figure,
the momentum of the flow before the jump equals
the momentum of the flow after the jump.
The momentum of the flow is given by:
M =
2Q2
gbh
+
h2b
4
If momentum before and after the jump is
unchanged, then the he diagram shows merely
that kinetic and potential energy changes equal
one another.
Another significant graph of hydraulic jump
data is of depth ratio h2/h1 (vertical axis) as a
function of the upstream Froude number, Fr1 (=
Q2/gb2h1
3 ). Construct such a graph for any of the
jumps for which you have taken measurements.
FIGURE 13.2. Momentum
diagram for a
hydraulic jump.
h1
h
M
Fr1 < 1
Fr2 > 1
zcr
Mmin
h2

45. 45
EXPERIMENT 14
MEASUREMENT OF PUMP PERFORMANCE
The objective of this experiment is to perform
a test of a centrifugal pump and display the
results in the form of what is known as a
performance map.
Figure 14.1 is a schematic of the pump and
piping system used in this experiment. The pump
contains an impeller within its housing. The
impeller is attached to the shaft of the motor
and the motor is mounted so that it is free to
rotate, within limits. As the motor rotates and
the impeller moves liquid through the pump, the
motor housing tends to rotate in the opposite
direction from that of the impeller. A calibrated
measurement system gives a readout of the torque
exerted by the motor on the impeller.
The rotational speed of the motor is obtained
with a tachometer. The product of rotational
speed and torque is the input power to the
impeller from the motor.
Gages in the inlet and outlet lines about the
pump give the corresponding pressures in gage
pressure units. The gages are located at known
heights from a reference plane.
After moving through the system, the water
is discharged into an open channel containing a
V-notch weir. The weir is calibrated to provide
the volume flow rate through the system.
The valve in the outlet line is used to control
the volume flow rate. As far as the pump is
concerned, the resistance offered by the valve
simulates a piping system with a controllable
friction loss. Thus for any valve position, the
following data can be obtained: torque, rotational
speed, inlet pressure, outlet pressure, and volume
flow rate. These parameters are summarized in
Table 14.1.
TABLE 14.1. Pump testing parameters.
Raw Data
Parameter Symbol Dimensions
torque T F·L
rotational speed ω 1/T
inlet pressure p1 F/L2
outlet pressure p2 F/L2
volume flow rate Q L3/T
The parameters used to characterize the
pump are calculated with the raw data obtained
from the test (listed above) and are as follows:
input power to the pump, the total head
difference as outlet minus inlet, the power
imparted to the liquid, and the efficiency. These
parameters are summarized in Table 14.2. These
parameters must be expressed in a consistent set of
units.
TABLE 14.2. Pump characterization parameters.
Reduced Data
Parameter Symbol Dimensions
input power dWa/dt F·L/T
total head diff ∆H L
power to liquid dW/dt F·L/T
efficiency η —
The raw data are manipulated to obtain the
reduced data which in turn are used to
characterize the performance of the pump. The
input power to the pump from the motor is the
product of torque and rotational speed:
-
dWa
d t
= Tω (14.1)
where the negative sign is added as a matter of
convention. The total head at section 1, where
the inlet pressure is measured (see Figure 14.1), is
defined as
H1 =
p1
ρg
+
V1
2
2g
+ z1
where ρ is the liquid density and V1 (= Q/A) is
the velocity in the inlet line. Similarly, the
total head at position 2 where the outlet pressure
is measured is
H2 =
p2
ρg
+
V2
2
2g
+ z2
The total head difference is given by

46. 46
∆H = H2 - H1 =
p2
ρg
+
V2
2
2g
+ z2
-




p1
ρg
+
V1
2
2g
+ z1
The dimension of the head H is L (ft or m). The
power imparted to the liquid is calculated with
the steady flow energy equation applied from
section 1 to 2:
-
d W
d t
= m
·
g






p2
ρg
+
V2
2
2g
+ z2
-






p1
ρg
+
V1
2
2g
+ z1
In terms of total head H, we have
-
d W
d t
= m
·
g (H2 - H1) = m
·
g ∆H (14.2)
The efficiency is determined with
η =
d W / d t
d W a/dt
(14.3)
Experimental Method
The experimental technique used in obtaining
data depends on the desired method of expressing
performance characteristics. For this experiment,
data are taken on only one impeller-casing-motor
combination. One data point is first taken at a
certain valve setting and at a preselected
rotational speed. The valve setting would then be
changed and the speed control on the motor (not
shown in Figure 14.1) is adjusted if necessary so
that the rotational speed remains constant, and
the next set of data are obtained. This procedure
is continued until 6 data points are obtained for
one rotational speed.
Next, the rotational speed is changed and
the procedure is repeated. Four rotational speeds
should be used, and at least 6 data points per
rotational speed should be obtained.
•
sump tank
inlet
valve
valve
pump
motor
control panel
and gages
v-notch weir
return
1-1/2 nominal
schedule 40
PVC pipe
1 nominal
schedule 40
PVC pipe
pressure
tap
pressure
tap
•
z1
z2
motor
shaft
FIGURE 14.1. Centrifugal pump testing setup.

47. 47
Performance Map
A performance map is to be drawn to
summarize the performance of the pump over its
operating range. The performance map is a graph
if the total head ∆H versus flow rate Q
(horizontal axis). Four lines, corresponding to the
four pre-selected rotational speeds, would be
drawn. Each line has 6 data points, and the
efficiency at each point is calculated. Lines of
equal efficiency are then drawn, and the resulting
graph is known as a performance map. Figure 14.2
is an example of a performance map.
0 200 400 600 800
0
10
20
30
40
Volume flow rate in gallons per minute
Totalheadinft
3600 rpm
1760
2700
900
85%
80%
75%
75%
65%
65%
Efficiency in %
FIGURE 14.2. Example of a performance map of
one impeller-casing-motor combination
obtained at four different rotational speeds.
Dimensionless Graphs
To illustrate the importance of
dimensionless parameters, it is prudent to use the
data obtained in this experiment and produce a
dimensionless graph.
A dimensional analysis can be performed for
pumps to determine which dimensionless groups
are important. With regard to the flow of an
incompressible fluid through a pump, we wish to
relate three variables introduced thus far to the
flow parameters. The three variables of interest
here are the efficiency η, the energy transfer rate
g∆H, and the power dW/dt. These three
parameters are assumed to be functions of fluid
properties density ρ and viscosity µ, volume flow
rate through the machine Q, rotational speed ω,
and a characteristic dimension (usually impeller
diameter) D. We therefore write three functional
dependencies:
η = f1(ρ, µ, Q, ω, D )
g∆H = f2(ρ, µ, Q, ω, D)
d W
d t
= f3(ρ, µ, Q, ω, D)
Performing a dimensional analysis gives the
following results:
η = f1



ρωD2
µ
,
Q
ωD3
g∆H
ω2D2 = f2



ρωD2
µ
,
Q
ωD3
dW/dt
ρω3D5 = f3



ρωD2
µ
,
Q
ωD3
where
g∆H
ω2D2 = energy transfer coefficient
Q
ωD3 = volumetric flow coefficient
ρωD2
µ
= rotational Reynolds number
dW/dt
ρω3D5 = power coefficient
Experiments conducted with pumps show that the
rotational Reynolds number (ρωD2/µ) has a
smaller effect on the dependent variables than
does the flow coefficient. So for incompressible
flow through pumps, the preceding equations
reduce to
η ≈ f1



Q
ωD3 (14.4)
g∆H
ω2D2 ≈ f2



Q
ωD3 (14.5)
dW/dt
ρω3D5 ≈ f3



Q
ωD3 (14.6)
For this experiment, construct a graph of
efficiency, energy transfer coefficient, and power
coefficient all as functions of the volumetric flow
coefficient. Three different graphs can be drawn,
or all lines can be placed on the same set of axes.

48. 48
Specific Speed
A dimensionless group known as specific
speed can also be derived. Specific speed is found
by combining head coefficient and flow
coefficient in order to eliminate characteristic
length D:
ωss =



Q
ωD3
1/2



ω2D2
g∆H
3/4
or ωss =
ωQ1/2
(g∆H)3/4 [dimensionless]
Exponents other than 1/2 and 3/4 could be used (to
eliminate D), but 1/2 and 3/4 are customarily
selected for modeling pumps. Another definition
for specific speed is given by
ωs =
ωQ1/2
∆H3/4



rpm =
rpm(gpm)1/2
ft3/4
in which the rotational speed ω is expressed in
rpm, volume flow rate Q is in gpm, total head ∆H
is in ft of liquid, and specific speed ωs is
arbitrarily assigned the unit of rpm. The equation
for specific speed ωss is dimensionless whereas
ωs is not.
The specific speed of a pump can be
calculated at any operating point, but
customarily specific speed for a pump is
determined only at its maximum efficiency. For
the pump of this experiment, calculate its
specific speed using both equations.

49. 49
EXPERIMENT 15
MEASUREMENT OF VELOCITY
AND
CALIBRATION OF A METER FOR COMPRESSIBLE FLOW
The objective of this experiment is to
determine a calibration curve for a meter placed
in a pipe that is conveying air. The meters of
interest are an orifice meter and a venturi meter.
These meters are calibrated in this experiment by
using a pitot-static tube to measure the velocity,
from which the flow rate is calculated.
Pitot Static Tube
When a fluid flows through a pipe, it exerts
pressure that is made up of static and dynamic
components. The static pressure is indicated by a
measuring device moving with the flow or that
causes no velocity change in the flow. Usually, to
measure static pressure, a small hole
perpendicular to the flow is drilled through the
container wall and connected to a manometer (or
pressure gage) as indicated in Figure 15.1.
The dynamic pressure is due to the movement
of the fluid. The dynamic pressure and the static
pressure together make up the total or stagnation
pressure. The stagnation pressure can be measured
in the flow with a pitot tube. The pitot tube is an
open ended tube facing the flow directly. Figure
15.1 gives a sketch of the measurement of
stagnation pressure.
static pressure
measurement
stagnation pressure
measurement
pitot tube
flow
hh
FIGURE 15.1. Measurement of static and
stagnation pressures.
The pitot-static tube combines the effects of
static and stagnation pressure measurement into
one device. Figure 15.2 is a schematic of the pitot-
static tube. It consists of a tube within a tube
which is placed in the duct facing upstream. The
pressure tap that faces the flow directly gives a
measurement of the stagnation pressure, while
the tap that is perpendicular to the flow gives
the static pressure.
When the pitot-static tube is immersed in the
flow of a fluid, the pressure difference
(stagnation minus static) can be read directly
using a manometer and connecting the pressure
taps to each leg. Applying the Bernoulli equation
between the two pressure taps yields:
A
A
section A-A
enlarged
four to eight holes
equally spaced
manometer
connections
flow direction
FIGURE 15.2. Schematic of a pitot-static tube.
p1
ρg
+
V1
2
2g
+ z1 =
p2
ρg
+
V2
2
2g
+ z2
where state “1” as the stagnation state (which
will be changed to subscript “t”), and state “2” as
the static state (no subscript). Elevation
differences are negligible, and at the point where
stagnation pressure is measured, the velocity is
zero. The Bernoulli equation thus reduces to:
pt
ρg
=
p
ρg
+
V2
2g
Next, we rearrange the preceding equation and
solve for velocity
V =
√2(pt - p)
ρ
A manometer connected to the pitot-static tube
would provide head loss readings ∆h given by

50. 50
∆h =
pt - p
ρg
where density is that of the flowing fluid. So
velocity in terms of head loss is
V = √2g∆h
Note that this equation applies only to
incompressible flows. Compressibility effects are
not accounted for. Furthermore, ∆h is the head
loss in terms of the flowing fluid and not in terms
of the reading on the manometer.
For flow in a duct, manometer readings are to
be taken at a number of locations within the cross
section of the flow. The velocity profile is then
plotted using the results. Velocities at specific
points are then determined from these profiles.
The objective here is to obtain data, graph a
velocity profile and then determine the average
velocity.
Average Velocity
The average velocity is related to the flow
rate through a duct as
V =
Q
A
where Q is the volume flow rate and A is the
cross sectional area of the duct. We can divide
the flow area into five equal areas, as shown in
Figure 15.3. The velocity is to be obtained at
those locations labeled in the figure. The chosen
positions divide the cross section into five equal
concentric areas. The flow rate through each area
labeled from 1 to 5 is found as
Q1 = A1V1 Q2 = A2V2
Q3 = A3V3 Q4 = A4V4
Q5 = A5V5
0.316 R
R
0.837 R
0.949 R0.707 R
0.548 R
FIGURE 15.3. Five positions within the cross
section where velocity is to be determined.
The total flow rate through the entire cross
section is the sum of these:
Qtotal = ∑
1
5
Qi = A1V1 + A2V2 + A3V3 + A4V4
+ A5V5
or Qtotal = A1 (V1 + V2 + V3 + V4 + V5)
The total area Atotal is 5A1 and so
V =
Qtotal
Atotal
=
(Atotal/5)(V1 + V2 + V3 + V4 + V5)
Atotal
The average velocity then becomes
V =
(V1 + V2 + V3 + V4 + V5)
5
The importance of the five chosen radial
positions for measuring V1 through V5 is now
evident.
Velocity Measurements
Equipment
Axial flow fan apparatus
Pitot-static tube
Manometer
The fan of the apparatus is used to move air
through the system at a rate that is small enough
to allow the air to be considered incompressible.
While the fan is on, make velocity profile
measurements at a selected location within the
duct at a cross section that is several diameters
downstream of the fan. Repeat these
measurements at different fan speed settings so
that 9 velocity profiles will result. Use the
velocity profiles to determine the average
velocity and the flow rate.
Questions
1. Why is it appropriate to take velocity
measurements at several diameters
downstream of the fan?
2. Suppose the duct were divided into 6 equal
areas and measurements taken at select
positions in the cross section. Should the
average velocity using 6 equal areas be the
same as the average velocity using 5 or 4
equal areas?

51. 51
Incompressible Flow Through a Meter
Incompressible flow through a venturi and an
orifice meter was discussed in Experiment 9. For
our purposes here, we merely re-state the
equations for convenience. For an air over liquid
manometer, the theoretical equation for both
meters is
Qth = A2
√
2g∆h
(1 - D2
4/D1
4)
Now for any pressure drop ∆hi, there are two
corresponding flow rates: Qac and Qth. The ratio of
these flow rates is the venturi discharge
coefficient Cv, defined as
Cv =
Qac
Qth
= 0.985
for turbulent flow. The orifice discharge
coefficient can be expressed in terms of the Stolz
equation:
Co = 0.595 9 + 0.031 2β 2.1 - 0.184β 8 +
+ 0.002 9β 2.5



106
Re β
0.75
+ 0.09L1



β 4
1 - β 4 - L2 (0.003 37β 3)
where Re =
ρVoDo
µ
=
4ρQac
πDoµ
β =
Do
D1
L1 = 0 for corner taps
L1 = 1/D1 for flange taps
L1 = 1 for 1D &
1
2D taps
and if L1 ≥ 0.433 3, the coefficient of the



β 4
1 - β 4
term becomes 0.039.
L2 = 0 for corner taps
L2 = 1/D1 for flange taps
L2 = 0.5 - E/D1 for 1D &
1
2D taps
E = orifice plate thickness
Compressible Flow Through a Meter
When a compressible fluid (vapor or gas)
flows through a meter, compressibility effects
must be accounted for. This is done by introduction
of a compressibility factor which can be
determined analytically for some meters
(venturi). For an orifice meter, on the other hand,
the compressibility factor must be measured.
The equations and formulation developed
thus far were for incompressible flow through a
meter. For compressible flows, the derivation is
somewhat different. When the fluid flows
through a meter and encounters a change in area,
the velocity changes as does the pressure. When
pressure changes, the density of the fluid changes
and this effect must be accounted for in order to
obtain accurate results. To account for
compressibility, we will rewrite the descriptive
equations.
Venturi Meter
Consider isentropic, subsonic, steady flow of
an ideal gas through a venturi meter. The
continuity equation is
ρ1A1V1 = ρ2A2V2 =
·
misentropic =
·
ms
where section 1 is upstream of the meter, and
section 2 is at the throat. Neglecting changes in
potential energy (negligible compared to changes
in enthalpy), the energy equation is
h1 +
V1
2
2
= h2 +
V2
2
2
The enthalpy change can be found by assuming
that the compressible fluid is ideal:
h1 - h2 = Cp(T1 - T2)
Combining these equations and rearranging gives
CpT1 +
·
ms
2
2ρ1
2A1
2 = CpT2 +
·
ms
2
2ρ2
2A2
2
or
·
ms
2



1
ρ2
2A2
2 -
1
ρ1
2A1
2 = 2Cp(T1 - T2)
= 2CpT1



1 -
T2
T1
If we assume an isentropic compression process
through the meter, then we can write
p2
p1
=



T2
T1
γ
γ - 1
where γ is the ratio of specific heats (γ = Cp/Cv).
Also, recall that for an ideal gas,
Cp =
Rγ
γ - 1
Substituting, rearranging and simplifying, we get

52. 52
·
ms
2
ρ2
2A2
2



1 -
ρ2
2A2
2
ρ1
2A1
2 = 2
Rγ
γ - 1
T1






1 -



p2
p1
γ - 1
γ
For an ideal gas, we write ρ = p/RT. Substituting
for the RT1 term in the preceding equation yields
·
ms
2
A2
2 = 2ρ2
2 γ
γ - 1 


p1
ρ1
1 - (p2/p1) (γ - 1)/γ
1 - (ρ2
2A2
2/ρ1
2A1
2)
For an isentropic process, we can also write
p1
ρ1
γ =
p2
ρ2
γ
or ρ2 =



p2
p1
1/γ
ρ1
from which we obtain
ρ2
2 =



p2
p1
2/γ
ρ1
2
Substituting into the mass flow equation, we get
after considerable manipulation Equation 15.1 of
Table 15.1, which summarizes the results.
Thus for compressible flow through a venturi
meter, the measurements needed are p1, p2, T1,
the venturi dimensions, and the fluid properties.
By introducing the venturi discharge coefficient
Cv, the actual flow rate through the meter is
determined to be
·
mac = Cv
·
ms
Combining this result with Equation 15.1 gives
Equation 15.2 of Table 15.1.
It would be convenient if we could re-write
Equation 15.2 in such a way that the
compressibility effects could be consolidated into
one term. We attempt this by using the flow rate
equation for the incompressible case multiplied
by another coefficient called the compressibility
factor Y; we therefore write
·
mac = CvYρ1A2
√
2(p1 - p2)
ρ1(1 - D2
4/D1
4)
We now set the preceding equation equal to
Equation 15.2 and solve for Y. We obtain Equation
15.3 of the table.
The ratio of specific heats γ will be known for
a given compressible fluid, and so Equation 15.3
could be plotted as compressibility factor Y versus
pressure ratio p2/p1 for various values of D2/D1.
The advantage of using this approach is that a
pressure drop term appears just as with the
incompressible case, which is convenient if a
manometer is used to measure pressure. Moreover,
the compressibility effect has been isolated into
one factor Y.
Orifice Meter
The equations and formulation of an analysis
for an orifice meter is the same as that for the
venturi meter. The difference is in the evaluation
of the compressibility factor. For an orifice meter
the compressibility factor is much lower than
that for a venturi meter. The compressibility
factor for an orifice meter cannot be derived, but
instead must be measured. Results of such tests
have yielded the Buckingham equation, Equation
15.4 of Table 15.1, which is valid for most
manometer connection systems.
Calibration of a Meter
Figures 15.4 and 15.5 show how the apparatus
is set up. An axial flow fan is attached to the
shaft of a DC motor. The rotational speed of the
motor, and hence the volume flow rate of air, is
controllable. The fan moves air through a duct
into which a pitot-static tube is attached. The
pitot static tube is movable so that the velocity
at any radial location can be measured. An orifice
or a venturi meter can be placed in the duct
system.
The pitot static tube has pressure taps which
are to be connected to a manometer. Likewise each
meter also has pressure taps, and these will be
connected to a separate manometer.
A meter for calibration will be assigned by
the instructor. For the experiment, make
measurements of velocity using the pitot-static
tube to obtain a velocity profile. Draw the
velocity profile to scale. Obtain data from the
velocity profile and determine a volume flow
rate.
For one velocity profile, measure the pressure
drop associated with the meter. Graph volume
flow rate as a function of head loss ∆h obtained
from the meter, with ∆h on the horizontal axis.
Determine the value of the compressibility factor
experimentally and again using the appropriate
equation (Equation 15.3 or 15.4) for each data
point. A minimum of 9 data points should be
obtained. Compare the results of both
calculations for Y.

53. 53
TABLE 15.1. Summary of equations for compressible flow through a venturi or an orifice meter.
·
ms = A2





2p1ρ1 (p2/p1)2/γ [γ/(γ - 1)] [1 - (p2/p1)(γ - 1)/γ
]
1 - (p2/p1)2/γ (D2
4/D1
4)
1/2
(15.1)
·
mac = Cv A2





2p1ρ1 (p2/p1)2/γ [γ/(γ - 1)] [1 - (p2/p1)(γ - 1)/γ
]
1 - (p2/p1)2/γ (D2
4/D1
4)
1/2
(15.2)
Y =
√γ
γ - 1
[(p2/p1)2/γ - (p2/p1)(γ + 1)/γ](1 - D2
4/D1
4)
[1 - (D2
4/D1
4)(p2/p1)2/γ](1 - p2/p1)
(venturi meter) (15.3)
Y = 1 - (0.41 + 0.35β 4)
(1 - p2/p1)
γ
(orifice meter) (15.4)
rounded
inlet
outlet ductaxial flow
fan
motor
manometer
connections
pitot-static
tube
venturi meter
FIGURE 15.4. Experimental setup for calibrating a venturi meter.
rounded
inlet
outlet ductaxial flow
fan
motor
orifice plate
manometer
connections
pitot-static
tube
FIGURE 15.5. Experimental setup for calibrating an orifice meter.

54. 54
EXPERIMENT 16
MEASUREMENT OF FAN HORSEPOWER
The objective of this experiment is to measure
performance characteristics of an axial flow fan,
and display the results graphically.
Figure 16.1 shows a schematic of the
apparatus used in this experiment. A DC motor
rotates an axial flow fan which moves air
through a duct. The sketch shows a venturi meter
used in the outlet duct to measure flow rate.
However, an orifice meter or a pitot-static tube
can be used instead. (See Experiment 16.) The
control volume from section 1 to 2 includes all the
fluid inside. The inlet is labeled as section 1, and
has an area (indicated by the dotted line) so huge
that the velocity at 1 is negligible compared to
the velocity at 2. The pressure at 1 equals
atmospheric pressure. The fan thus accelerates
the flow from a velocity of 0 to a velocity we
identify as V2. The continuity equation is
m
·
1 = m
·
2
The energy equation is
0 = -
dW
d t
+ m
·
1



h1 +
V1
2
2
- m
·
2



h2 +
V2
2
2
where dW/dt is the power input from the fan to
the air, which is what we are solving for. By
substituting the enthalpy terms according to the
definition (h = u + pv), the preceding equation
becomes
d W
d t
= m
·
(u1 - u2)
+ m
·









p1
ρ
+
V1
2
2
-



p2
ρ
+
V2
2
2
Assuming ideal gas behavior, we have
u1 - u2 = Cv(T1 - T2)
With a fan, however, we assume an isothermal
process, so that T1 ≈ T2 and ρ1 ≈ ρ2 = ρ. With m
·
=
ρAV (evaluated at the outlet, section 2), the
equation for power becomes
d W
d t
= A2V2









p1 +
ρV1
2
2
-



p2 +
ρV2
2
2
Recall that in this analysis, we set up our control
volume so that the inlet velocity V1 = 0; actually
V1 << V2. Thus



p1 +
ρV1
2
2
-



p2 +
ρV2
2
2
≈



p1 - p2 -
ρV2
2
2
in which p1 is atmospheric pressure, and p2 is
measured at section 2. The quantity in brackets in
the previous equation is the change in total
pressure ∆pt. Thus, the power is
d W
d t
= ∆ptQ (16.1)
This is the power imparted to the air from the
fan.
Data Acquisition
The motor controller is used to set the
rotational speed of the fan, which in turn controls
the volume flow rate of air through the duct. On
the side of the motor is a shaft (a torque arm)
that extends outward normal to the axis of
rotation. When the fan rotates, the motor tends to
rotate in the opposite direction. A weight can be
rounded
inlet
outlet ductaxial flow
fan
motor
manometer
connections
venturi meter
1 2
FIGURE 16.1. Schematic of setup of fan horsepower experiment.

55. 55
placed on the torque arm to reposition the motor
to its balanced position. The product of weight
and torque arm length gives the torque input from
motor to fan.
A tachometer is used to measure the
rotational speed of the motor. The product of
torque and rotational speed gives the power input
to the fan:
dWa
d t
= Tω (16.2)
This is the power delivered to the fan from the
motor.
The efficiency of the fan can now be
calculated using Equations 1 and 2:
η =
d W / d t
d W a/dt
(16.3)
Thus for one setting of the motor controller, the
following readings should be obtained:
1. An appropriate reading for the flow meter.
2. Weight needed to balance the motor, and its
position on the torque arm.
3. Rotational speed of the fan and motor.
4. The static pressure at section 2.
With these data, the following parameters
can be calculated, again for each setting of the
motor controller:
1. Outlet velocity at section 2: V2 = Q/A2.
2. The power using Equation 16.1.
3. The input power using Equation 16.2.
4. The efficiency using Equation 16.3.
Presentation of Results
On the horizontal axis, plot volume flow
rate. On the vertical axis, graph the power using
Equation 1, and Equation 2, both on the same set of
axes. Also, again on the same set of axes, graph
total pressure ∆pt as a function of flow rate. On a
separate graph, plot efficiency versus flow rate
(horizontal axis).

56. 56
EXPERIMENT 17
EXTERNAL LAMINAR FLOWS OVER IMMERSED BODIES
The flow of fluid over an immersed body is
called an external flow. There are qualitative
explanations for the behavior of flows over
bodies. Purely analytic solutions to flow fields
are limited to only a few simple geometries.
External flows are characterized by two regions
in the flow field—the viscous boundary layer
near the solid surface of the body, and the
inviscid free stream. For flow past some immersed
bodies, the boundary layer can separate when the
flow near the body develops an adverse pressure
gradient, resulting in a region of flow reversal.
Locating the point of separation is important
when analyzing external flows, because the
location will have a significant impact on the
pressure distribution and on the corresponding
forces acting on the body.
Hele-Shaw flows are a special class of
external flows where a body is positioned
between two parallel flat plates and the Re < 1.
The resulting pattern of streamlines for these
creeping laminar flows is identical to the
potential or inviscid flow solutions obtained
analytically.
Equipment
Laminar Flow Table Apparatus
Digital Camera
Available Shapes
(use those assigned by the instructor)
Cylinder (disk)
Rectangle
Airfoil
Venturi
Figure 17.1 is a schematic of the laminar flow
table used in this experiment. The apparatus
consists of a one piece base made of fiberglas with
water reservoirs at each end. Water enters the
upstream reservoir and flows over the lower
surface of the device to the downstream tank.
Water leaves this tank and goes to the drain.
A glass cover can be placed over the table and
body to model what is referred to as inviscid
Hele-Shaw flow behavior. Alternatively, the
glass cover is removed to observe the influence of
the viscous boundary layer on the flow. The lower
surface is marked with a grid to aid in
observation and orientation of the bodies. Eight
small holes in the table surface (not shown in the
sketch) allow for the introduction of source and
sink flows. Control valves for each of the eight
source and sink holes are also included in the
apparatus.
Mounted at the back of the table is the dye
reservoir. A valve at the base of this reservoir
controls the flow of the dye, used for
visualization of the flow, to the injection needles
positioned at the entrance of the table surface.
Procedure
Begin by filling the source reservoir with
water. Water will fill the reservoir until it
reaches the level of the marked table surface. As
a result of the incline of the apparatus, the water
should flow down in a thin sheet along the table
surface. If the glass cover is in place, then the
water should be flowing between the table
surface and the glass cover. Any air pockets
should be evacuated before injecting the dye.
Place the desired body on the table surface and
begin injecting the dye. Data collection, in the
form of digital photos, can begin once the flow
has reached steady-state. Source and sink flows
may be added to obtain other classic flows, such
as flow past a Rankine Oval.
Questions
1. How do the observed flow patterns for the
Hele-Shaw flows compare to published
inviscid (potential) flow analytic
solutions? Discuss your results and include
your sources in the discussion.
2. How do the observed flow patterns for the
boundary layer flows compare to other
published experimental results or analytic
solutions? Discuss your results and include
your sources in the discussion.
3. In observing (non Hele-Shaw) flow past a
cylinder, would you expect the separation
points on the cylinder to shift location if
the flow rate were increased? Why or why
not?
4. Are the dye lines observed on the Laminar
Flow Table Apparatus streamlines,
streaklines, or both? Explain your answer.
Acknowledgements
To Dr. Jeffrey Marchetta for implementing this
experiment, and to Darrin Bevard for getting the
apparatus installed and working.

57. 57
removable glass cover
dye reservoir
valve
manifold with injectors
dye water flow
water inlet
to drain
plan
view
profile
view
grid on surface
beneath glass
manifold with injectors
grid on surface
beneath glass
circular
disk
circular
disk
FIGURE 17.1. Plan and profile views of the laminar flow table. The setup is for Hele-Shaw flow past a
cylinder.

58. 58
EXPERIMENT 18
SERIES-PARALLEL PUMP PERFORMANCE
The objective of this experiment is to make
measurements on an apparatus that contains
two identical pumps, and determine: (a) the
performance of one of the pumps; (b) the
performance of both pumps while operating in
series; and, (c) the performance of both pumps
while operating in parallel.
Figure 18.1 is a sketch of the apparatus. A
water tank acts as a supply reservior from
which water is pumped. For individual pump
performance, we use pump (1). Water is pumped
from the tank through the valve at B. It is
discharged through the valve at A, with valve
D closed. Valve E is used as a flow control
valve, while the others are used for on-off
operation.
For series pump operation, pump (1) takes
in water with valve B fully open. Water is
discharged with the valve at A closed, the
valve at D fully open, and the valve at C
closed. Thus, flow that is discharged from
pump (1) enters pump (2). The water from pump
(2) is discharged through valve E which is the
flow control valve.
For parallel operation, the valves at B and
C are both open, and the valve at D is closed.
Valves A and E are both open with the valve
at E used to control the flow. Thus both pumps
operate simultaneously, with the discharge
from both combined through the flow control
valve.
Measurement and Control Systems
Both motors are controlled by external
rotary rheostats, and for series or parallel
operation, should be run at the same power
setting. Rotational speed sensors are mounted on
each motor housing. There are flow meters at
the outlet of each pump and in the pump just
downstream of valve E. Attached to the flow
meters are differential pressure sensors.
Upstream of pump (1) is a temperature sensor.
Output from all sensors is transmitted to an
electronics circuit, which transmits signals to a
computer. Measurements taken are compiled
and displayed by a computer, which removes
the need to take measurements manually, and
to analyze the results “by hand.” The sensors
and the electronics systems are already
connected to the computer, and the programs
needed for analysis are loaded. The computer
will produce performance graphs and tables for
any of the experiments.
centrifugal
pump (1)
centrifugal
pump (2)
motor
motor
water tank
A
B
C
DE
differential
pressure
sensor
differential
pressure
sensor
rotational
speed
sensor
temperature
sensor
FIGURE 18.1. Schematic of the series-parallel pump apparatus.

59. 59
Single Pump Performance
The objective here is to obtain a head flow
curve (∆H vs Q) for a centrifugal pump
operating at one speed.
Procedure
• Launch the program FM21SNGL on the
computer.
• Use pump (1) and be sure that the valves
are set appropriately: valves A, B, and E
are open. Valves C and D are closed.
• Start pump (1); pump (2) should remain off.
Decide on a power setting for pump (1) [such
as 50% or 75% or 100%] and set its controller
accordingly. This setting is used for this
and the subsequent experiments.
• Select “Diagrm” and note the value of the
volume flow rate displayed by the
computer.
• Decide on suitable increments to use for flow
rate so that typically 15 data points are
obtained between zero and maximum flow
rate.
• Close valve E for the condition of no flow
(Q = 0). When the readings on the screen
become sufficiently steady, select “Take
Sample.” This is the first data point. DO
NOT allow the pump to operate at zero
flow for any longer than necessary.
• Open valve E slightly to the first increment
in flow rate decided upon earlier. When
the readings are sufficiently steady, select
“Take Sample.”
• Repeat the previous step for other settings
of valve E, corresponding to increasing
values of flow rate. The last sample point
corresponds to valve E being fully open.
• The recorded data set can now be examined
via any of the selectable options:
“Graphs,” “Tables,” or downloaded into a
spreadsheet. Select the “Graphs” option
and obtain a head versus flow rate curve.
(See software help screens if necessary.)
Series Pump Performance
The objective here is to obtain a head flow
curve (∆H vs Q) for a two identical centrifugal
pumps operating at the same speed, and
operated such the flow leaving pump (1) enters
that of pump (2). When two pumps operate in
series, the combined head versus flow rate
curves is found by adding the heads of the
single pump curves at the same flow rates.
Procedure
• Launch the program FM21SERS on the
computer.
• Use both pumps and be sure that the valves
are set appropriately: valve A is closed.
All other valves are open.
• Start both pumps, and set them on the same
power setting that was used in the single
pump experiment. This setting is used for
this and the subsequent experiment.
• Select “Diagrm” and note the value of the
volume flow rate displayed by the
computer.
• Decide on suitable increments to use for flow
rate so that typically 15 data points are
obtained between zero and maximum flow
rate.
• Close valve E for the condition of no flow
(Q = 0). When the readings on the screen
become sufficiently steady, select “Take
Sample.” This is the first data point. DO
NOT allow the pump to operate at zero
flow for any longer than necessary.
• Open valve E slightly to the first increment
in flow rate decided upon earlier. When
the readings are sufficiently steady, select
“Take Sample.”
• Repeat the previous step for other settings
of valve E, corresponding to increasing
values of flow rate. The last sample point
corresponds to valve E being fully open.
• The recorded data set can now be examined
via any of the selectable options:
“Graphs,” “Tables,” or downloaded into a
spreadsheet. Select the “Graphs” option
and obtain a head versus flow rate curve.
(See software help screens if necessary.)
Parallel Pump Performance
The objective here is to obtain a head flow
curve (∆H vs Q) for a two identical centrifugal
pumps operating at the same speed, and
operated in parallel. Both pumps take in water
from the tank, and discharge the water into a
common line containing the valve at E. When
two pumps operate in parallel, the combined
head versus flow rate curves is found by adding
the flow rates of the single pump curves at the
same head.
Procedure
• Launch the program FM21PARA on the
computer.
• Use both pumps and be sure that the valves
are set appropriately: valve D is closed.
All other valves are open. .
• Start both pumps, and set them on the same
power setting that was used in the single
pump experiment.

60. 60
• Click on the button “single/parallel” on the
“Diagrm” screen. Note that the computer
can analyze data for single or for parallel
pump operation. (Single pump operation
was already completed, but if it was not, it
can be performed while the pumps are
operating in parallel.)
• Note the value of the volume flow rate
displayed by the computer.
• Decide on suitable increments to use for flow
rate so that typically 15 data points are
obtained between zero and maximum flow
rate.
• Close valve E for the condition of no flow
(Q = 0). When the readings on the screen
become sufficiently steady, select “Take
Sample.” This is the first data point. DO
NOT allow the pump to operate at zero
flow for any longer than necessary.
• Open valve E slightly to the first increment
in flow rate decided upon earlier. When
the readings are sufficiently steady, select
“Take Sample.”
• Repeat the previous step for other settings
of valve E, corresponding to increasing
values of flow rate. The last sample point
corresponds to valve E being fully open.
• The recorded data set can now be examined
via any of the selectable options:
“Graphs,” “Tables,” or downloaded into a
spreadsheet. Select the “Graphs” option
and obtain a head versus flow rate curve.
(See software help screens if necessary.)
Results
Compare the results obtained from this
experiment. Do the head versus flow rate
curves come out as expected; i.e., as illustrated
in Figure 18.2? Select several data points and
make calculations to verify the performance
graphs. What conclusions can be drawn
regarding series and parallel pump operation?
Is the use of the computer more convenient than
making calculations and producing graphs by
hand (or with a spreadsheet)?

61. 61
two pumps
one pump
H
H2
H1
Q
any Q
H
two pumps
one pump
Q
any H
Q1 Q2
series pump performance
for any Q
∆H2 = 2∆H1
parallel pump performance
for any ∆H
Q2 = 2Q1
FIGURE 18.2. Performance graphs for series and parallel pump configurations.

62. 62
EXPERIMENT 19
DESIGN OF EXPERIMENTS:
CALIBRATION OF AN ELBOW METER
There are many types of meters that can be
installed in a pipeline—venturi, orifice,
rotameter, and turbine-type. These meters can all
be calibrated to provide a reading of the volume
flow rate of fluid through the pipe.
An alternative, less expensive flow meter—
known as an elbow meter—can also be used. For an
existing pipeline containing elbows, an elbow
meter is perhaps the easiest meter to set up. All
that would be required is to drill and tap a couple
of holes in the elbow, and attach them to a
device for measuring pressure drop. Information
on an elbow meter is available from [1]. A sketch
of an elbow meter is shown in Figure 19.1
flow
D
R
45o
pressure
tap
FIGURE 19.1. Schematic of an elbow meter
showing pressure tap locations.
Installation. It is necessary to select an elbow in a
line where flow rate is to be measured. The
internal dimensions of R and D must be known for
the elbow of interest. Holes are drilled in specific
locations as shown to accept 1/8th nominal pipe
threads or something different if desired.
Pressure measurements are made to determine
the pressure drop that exists as well as the
corresponding flow rate.
Theory. The pressure measurement devices are
attached to the connectors and flow through the
pipe is initiated. The difference in pressure
between the tap locations is to be determined.
As given in [1], the flow rate through the
meter can be calculated with:
Q = A K
√
R
D
∆ p
ρ
where
A = cross sectional area = πD2/4 in ft2
K= 1 -
6.5
√Re
= correction factor (19.1)
Re = Reynolds number = ρVD/µ
104 ≤ Re ≤ 106
ρ = fluid density in slug/ft3
µ = fluid viscosity in lbf·s/ft2
∆p = pressure drop in lbf/ft2
D = diameter in ft
R = radius of elbow in ft
Sample Calculation. Show how flow rate is
calculated using a 4 nominal schedule 80 short
radius elbow meter. Pressure is measured with a
manometer. Water is the working fluid.
Solution: For a 4 nominal, short radius elbow we
have [2]:
R = 4 in. = 0.333 ft D = 0.3198 ft
We calculate
A =
πD2
4
=
π(0.3198)2
4
= 0.0803 ft2
For water,
ρ = 1.94 slug/ft3 µ = 1.9 x 10-5 lbf·s/ft2
A calibration curve is one that relates the volume
flow rate through the meter to the pressure drop,
using whatever units are convenient. We are
calculating the calibration results for only one
data point in such a curve. In this example, we
measure flow rate in gpm, and because we are
using a manometer, we express pressure drop in

63. 63
terms of inches of water. A sample calculation for
a flow rate of, say, 150 gpm is as follows. We
have
Q = 150 gpm (2.229 x 10-3) = 0.334 ft3/s
The flow velocity then is
V =
Q
A
=
0.334
0.0803
= 4.16 ft/s
To find ∆p, we must first find K which in turn
depends on Reynolds number:
Re=
ρVD
µ
=
1.94(4.16)(0.3198)
1.9 x 10-5 = 1.36 x 105
Then
K = 1 -
6.5
√Re
= 1 -
6.5
√1.36 x 105
= 0.982
For an elbow meter,
Q = A K
√
R
D
∆ p
ρ
Rearranging and solving for ∆p gives
∆p = ρ



Q
A K
2 D
R
(19.2)
Substituting
∆p = (1.94)



0.334
0.0803(0.982)
2 0.3198
0.333
or ∆p = 33.4 lbf/ft2
Now in terms of a column of water,
∆h =
∆p
ρg
=
33.4
1.94(32.2)
= 0.534 ft of water
or ∆h = 6.41 in. of water
For calculations of this type on an elbow that has
not been tested in the laboratory, the result is
accurate to within ± 4%. That is, for a reading ∆h
of 6.41 in. of water, the flow rate can be as high
as 156 gpm or as low as 144 gpm. Note that a
manometer is not readable to the nearest
hundredth of an inch. Typically a reading will be
to the nearest tenth of an inch.
So based on the results here, one data point on
the calibration curve is:
∆h = 6.4 in of water Q = 150 gpm
Calibration. In the preceding calculation, note
the dependence of the results on having an
equation for the correction factor K (Equation
19.1). The equation for K was derived from
theoretical considerations [1], but it is desirable
to have experimental results to determine a
“better” relationship for it. We could use
Equation 19.2 with experimental data to
determine K, which is the subject of this exercise.
Thus, if we had an apparatus that is set up
and ready to use, we could measure flow rate Q,
determine R and D from a handbook [2], calculate
A, and reduce Equation 19.2 to:
∆p = (a known constant) x



Q
K
2
(19.3)
Then with the apparatus, we could obtain ∆p vs
Q for a number of data points. Using Equation
19.3, we could then calculate K.
Experiment Design
1. Design an apparatus for making measurements
on an elbow meter. It is desired to have the
capability of making measurements on 3/4, 1 and
1 1/2 inch line sizes/elbows. A sketch of the
apparatus is required, showing:
a) what fluid is to be used
b) the prime mover for pumping the fluid
c) where the fluid is to be stored
d) an accurate method for determining actual
flow rate
2. Write a procedure for the operator(s) to follow
in order to obtain the desired data.
3. Write a theory section that leads the reader
through a sample calculation and shows
specifically how the correction factor K is
determined.
4. How many data points should be obtained so
that K can be determined with 95% confidence?
References
[1] Fluid Meters: Their Theory and Application,
6th edition, 1971, ASME, New York, page 75.
[2] (Perry’s Chemical Engineering Handbook, pg.
6-57.

64. 64
EXPERIMENT 20
DESIGN OF EXPERIMENTS:
MEASUREMENT OF FORCE ON A CONICAL OBJECT
A jet of fluid striking a stationary object
exerts a force on that object. This force can be
measured when the object is connected to a spring
balance or scale. The force can then be related to
the velocity of the jet of fluid and in turn to the
rate of flow. This was the subject of the Impact of
a Jet of Water experiment, in which the force
exerted by a water jet on a flat plate or a
hemisphere was measured. Calculations were
made to theoretically predict this force, and
were compared to the measured results.
The force developed by a jet stream of water
directed at a concave cone is the subject of this
experiment.
Figure 20.1 is a schematic of the device used
in this experiment. The device consists of a tank
within a tank. The interior tank is supported on a
pivot and has a lever arm attached to it. As
water enters this inner tank, the lever arm will
reach a balance point. At this time, a stopwatch
is started and a weight is placed on the weight
hanger (e.g., 10 lbf). When enough water has
entered the tank (10 lbf), the lever arm will
again balance. The stopwatch is stopped. The
elapsed time divided into the weight of water
collected gives the weight or mass flow rate of
water through the system (lbf/sec, for example).
The outer tank acts as a support for the table
top as well as a sump tank. Water is pumped from
the outer tank to the apparatus resting on the
table top. As shown in Figure 20.1, the impact
apparatus contains a nozzle that produces a high
velocity jet of water. The jet is aimed at an object
(such as a flat plate or hemisphere). The force
exerted on the plate causes the balance arm to
which the plate is attached to deflect. A weight
is moved on the arm until the arm balances. A
summation of moments about the pivot point of
the arm allows for calculating the force exerted
by the jet.
Water is fed through the nozzle by means of
a centrifugal pump. The nozzle emits the water in
a jet stream whose diameter is constant. After the
water strikes the object, the water is channeled to
the weighing tank inside to obtain the weight or
mass flow rate.
The variables involved in this experiment
are listed and their measurements are described
below:
1. Mass rate of flow–measured with the
weighing tank inside the sump tank. The
volume flow rate is obtained by dividing
mass flow rate by density: Q = m/ρ.
2. Velocity of jet–obtained by dividing volume
flow rate by jet area: V = Q/A. The jet is
cylindrical in shape with a diameter of 0.375
in.
3. Resultant force—found experimentally by
summation of moments about the pivot point
of the balance arm. The theoretical resultant
force is found by use of an equation derived by
applying the momentum equation to a control
volume about the plate.
Impact Force Analysis
The total force exerted by the jet equals the
rate of momentum loss experienced by the jet after
it impacts the object. For a cone, as shown in
Figure 20.2, whose included half angle is α,
F =
ρQ2
A
(1 + cos α) (20.1)
A
A
FIGURE 20.2. A schematic of a conical impact
object.
Experiment Design
1. Design a conical object to be used with the
apparatus in the lab; i.e., the apparatus used in
Experiment 5. The cone dimensions must be
selected as well as a method for mounting the
cone in the apparatus. Prepare a dimensioned
drawing of your design.

65. 65
2. The method of making flow rate measurements
is believed to be antiquated, and should be
replaced with another method. Determine an
alternative method of measuring flow rate that
is compatible with the apparatus used in
Experiment 4. The instrument(s) selected should
have a digital readout, and should provide data
in appropriate units.
3. Write a procedure for the operator(s) to follow
in order to obtain the desired data.
4. Write a theory section that leads the reader
through a sample calculation and shows
specifically how Equation 20.1 is derived.
flat plate
pivot
balancing weight lever arm with
flat plate attached
water
jet nozzle
drain
weigh tank
plug
sump tank
motor pump
weight hanger
flow control
valve
tank
pivot
FIGURE 20.1. A schematic of the jet impact apparatus.

66. 66
Appendix
Calibration Curves
V-notch weir—turbomachinery experiments

67. 67
0 50 100 150 200 250 300 350
0
20
40
60
80
100
120
volume flow rate in liters/min
heightreadinginmm
FIGURE A.2. Calibration curve for the V-notch weir, turbomachinery experiments.