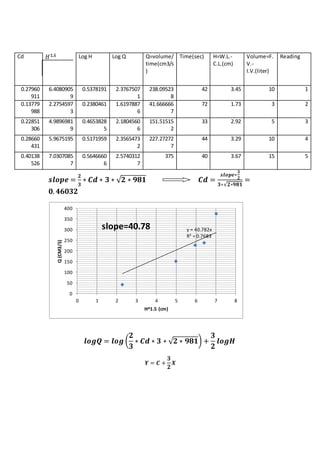
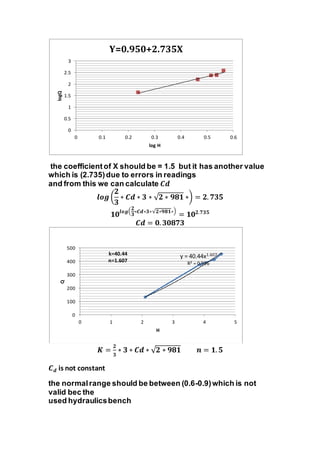
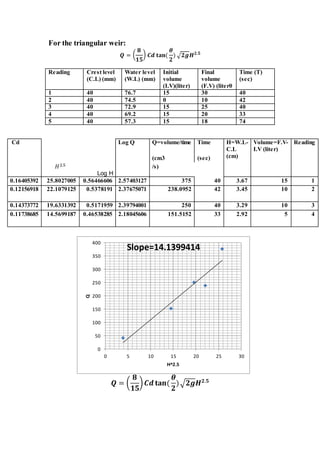
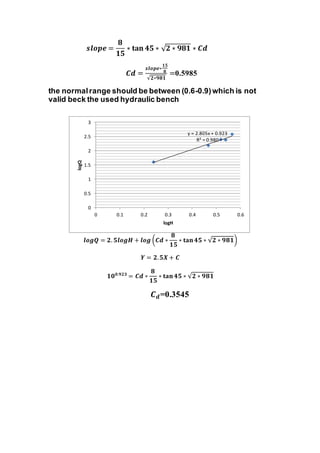
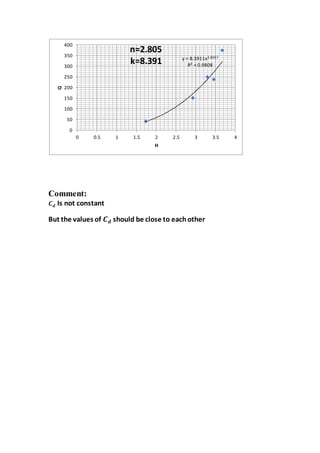
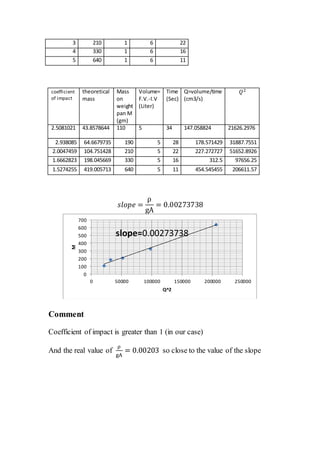
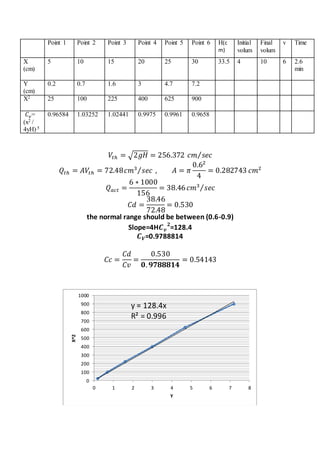
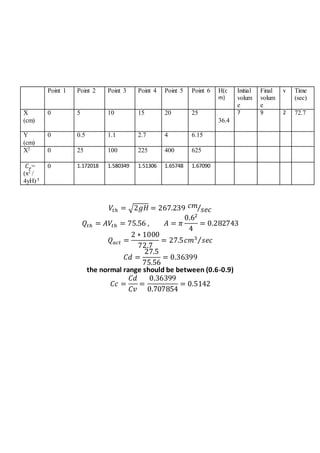
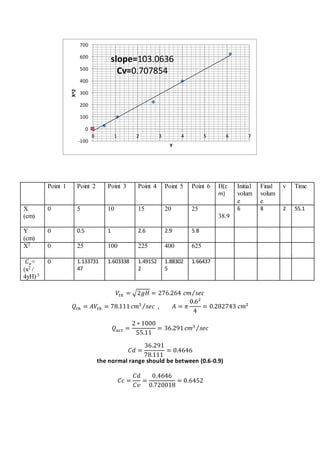
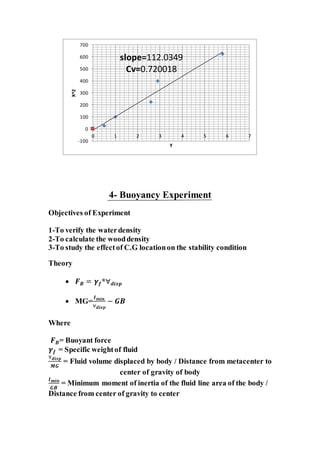
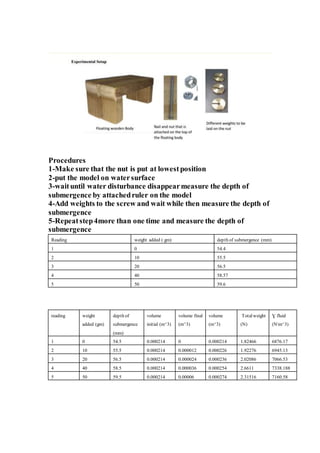
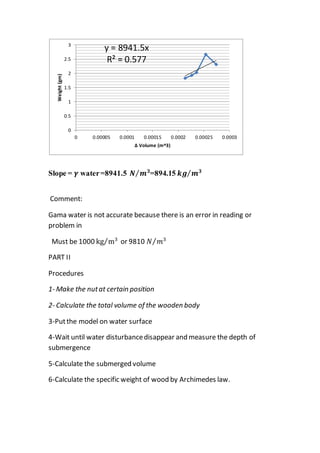
The report documents various fluid mechanics experiments conducted at Cairo University, focusing on weir types, the impact of water jets, and flow through orifices. Key objectives include calculating discharge coefficients, understanding jet dynamics, and measuring flow characteristics. Results indicate deviations from expected discharge coefficients, highlighting experimental errors and the importance of precise measurements.

1. Cairo University
Faculty of Engineering
Civil Engineering Department
2015-2016
Fluid Mechanics
Lab Report
BY: Almoutaz Alsaeed

2. 1. Weir Experiment (Rectangular and Triangular)
Objectives of the Experiment
1. To demonstrate the flow over different weir types.
2. To calculate the coefficient of discharge for different weir types.
3. To study the variation and dependence of the relevant parameters.
Theory
For the rectangularweir:
𝑸 = (
𝟐
𝟑
) 𝑪𝒅𝑩√ 𝟐𝒈𝑯 𝟏.𝟓
For the triangular weir:
𝑸 = (
𝟖
𝟏𝟓
) 𝑪𝒅 𝐭𝐚𝐧(
𝜽
𝟐
)√ 𝟐𝒈𝑯 𝟐.𝟓
where
Cd = Coefficientof discharge
B = width of the rectangularweir (3 cm)
H = head above the weir crestor apex
θ = angle of the triangular weir
g = accelerationof gravity
Experimental Setup

3. Procedures and Readings
1. Make sure that the Hydraulic Bench is levelled.
2. Set the Venire on the point gauge to a datum reading by placing the tip
of the gauge on the crest or the apex of the weir. Take enough care not
damage the weir plate and the point gauge
.
3. Put the point gauge half way between the stilling baffle plate and the
weir plate.
4. Allow water to flow into the experimental setup and adjust the
minimum flow rate by means of the control valve to have atmospheric
pressure all around water flowing over the weir. Increase the flow rate
incrementally such that the head above the weir crest increases around 1
cm for each flow rate increment
5. Foreach flow rate, wait until steady condition is attained then measure
and record the head(H) above the weir.
6. Foreach flow rate, measure and record the initial and final volumes in
the collecting tank and the time required to collect that volume. For each
flow rate, take 3 different readings of
the volumes and time and record the averages
For the rectangularweir:
𝑸 = 𝑪 𝒅.
𝟐
𝟑
. 𝑩.√ 𝟐𝒈 𝑯
𝟑
𝟐
Reading Crest level
(C.L) (cm )
Water level
(W.L)(cm)
Initial
volume
(I.V)(liter)
Final
volume
(F.V)(liter)
Time (T)
(sec)
1 4 7.45 0 10 42
2 4 5.73 15 18 72
3 4 6.92 15 20 33
4 4 7.29 15 25 44
5 4 7.67 15 30 40

4. ReadingVolume=F.
V.-
I.V.(liter)
H=W.L.-
C.L.(cm)
Time(sec)Q=volume/
time(cm3/s
)
Log QLog HCd
1103.4542238.09523
8
2.3767507
1
0.53781916.4080905
9
0.27960
911
231.737241.666666
7
1.6197887
6
0.23804612.2754597
3
0.13779
988
352.9233151.51515
2
2.1804560
6
0.4653828
5
4.9896981
9
0.22851
306
4103.2944227.27272
7
2.3565473
2
0.51719595.96751950.28660
431
5153.67403752.5740312
7
0.5646660
6
7.0307085
7
0.40138
526
𝒔𝒍𝒐𝒑𝒆 =
𝟐
𝟑
∗ 𝑪𝒅 ∗ 𝟑 ∗ √ 𝟐 ∗ 𝟗𝟖𝟏 𝑪𝒅 =
𝒔𝒍𝒐𝒑𝒆∗
𝟑
𝟐
𝟑∗√𝟐∗𝟗𝟖𝟏
=
𝟎. 𝟒𝟔𝟎𝟑𝟐
𝒍𝒐𝒈𝑸 = 𝒍𝒐𝒈 (
𝟐
𝟑
∗ 𝑪𝒅 ∗ 𝟑 ∗ √ 𝟐 ∗ 𝟗𝟖𝟏) +
𝟑
𝟐
𝒍𝒐𝒈𝑯
𝒀 = 𝑪 +
𝟑
𝟐
𝑿
y = 40.782x
R² = 0.7683
0
50
100
150
200
250
300
350
400
0 1 2 3 4 5 6 7 8
Q(CM3/S)
H^1.5 (cm)
slope=40.78

5. the coefficient of X should be = 1.5 but it has another value
which is (2.735)due to errors in readings
and from this we can calculate 𝑪𝒅
𝒍𝒐𝒈 (
𝟐
𝟑
∗ 𝑪𝒅 ∗ 𝟑 ∗ √ 𝟐 ∗ 𝟗𝟖𝟏 ∗) = 𝟐. 𝟕𝟑𝟓
𝟏𝟎𝒍𝒐𝒈(
𝟐
𝟑
∗𝑪𝒅∗𝟑∗√𝟐∗𝟗𝟖𝟏∗)
= 𝟏𝟎 𝟐.𝟕𝟑𝟓
𝑪𝒅 = 𝟎. 𝟑𝟎𝟖𝟕𝟑
𝑲 =
𝟐
𝟑
∗ 𝟑 ∗ 𝑪𝒅 ∗ √ 𝟐 ∗ 𝟗𝟖𝟏 𝒏 = 𝟏. 𝟓
𝑪 𝒅 is not constant
the normalrange should be between (0.6-0.9)which is not
valid bec the
used hydraulicsbench
0
0.5
1
1.5
2
2.5
3
0 0.1 0.2 0.3 0.4 0.5 0.6
logQ
log H
Y=0.950+2.735X
y = 40.44x1.607
R² = 0.996
0
100
200
300
400
500
0 1 2 3 4 5
Q
H
k=40.44
n=1.607

6. For the triangular weir:
𝑸 = (
𝟖
𝟏𝟓
) 𝑪𝒅 𝐭𝐚𝐧(
𝜽
𝟐
) √𝟐𝒈𝑯 𝟐.𝟓
Reading Crest level
(C.L) (mm)
Water level
(W.L) (mm)
Initial
volume
(I.V)(liter)
Final
volume
(F.V) (liter0
Time (T)
(sec)
1 40 76.7 15 30 40
2 40 74.5 0 10 42
3 40 72.9 15 25 40
4 40 69.2 15 20 33
5 40 57.3 15 18 74
ReadingVolume=F.V-
I.V (liter)
H=W.L-
C.L
(cm)
TimeQ=volume/timeLog Q
Log H
𝐻2.5
Cd
(sec)(cm3
/s)
1153.67403752.574031270.5646660625.80270050.16405392
2103.4542238.09522.376750710.537819122.10791250.12156918
3103.29402502.397940010.517195919.63313920.14373772
452.9233151.51522.180456060.4653828514.56991870.11738685
𝑸 = (
𝟖
𝟏𝟓
) 𝑪𝒅 𝐭𝐚𝐧(
𝜽
𝟐
)√ 𝟐𝒈𝑯 𝟐.𝟓
0
50
100
150
200
250
300
350
400
0 5 10 15 20 25 30
Q
H^2.5
Slope=14.1399414

7. 𝒔𝒍𝒐𝒑𝒆 =
𝟖
𝟏𝟓
∗ 𝐭𝐚𝐧 𝟒𝟓 ∗ √ 𝟐 ∗ 𝟗𝟖𝟏 ∗ 𝑪𝒅
𝑪𝒅 =
𝒔𝒍𝒐𝒑𝒆∗
𝟏𝟓
𝟖
√𝟐∗𝟗𝟖𝟏
=0.5985
the normalrange should be between (0.6-0.9)which is not
valid beck the used hydraulic bench
𝒍𝒐𝒈𝑸 = 𝟐. 𝟓𝒍𝒐𝒈𝑯 + 𝒍𝒐𝒈 (𝑪𝒅 ∗
𝟖
𝟏𝟓
∗ 𝐭𝐚𝐧 𝟒𝟓 ∗ √𝟐 ∗ 𝟗𝟖𝟏)
𝒀 = 𝟐. 𝟓𝑿 + 𝑪
𝟏𝟎 𝟎.𝟗𝟐𝟑
= 𝑪𝒅 ∗
𝟖
𝟏𝟓
∗ 𝐭𝐚𝐧 𝟒𝟓 ∗ √𝟐 ∗ 𝟗𝟖𝟏
𝑪 𝒅=0.3545
y = 2.805x + 0.923
R² = 0.980
0
0.5
1
1.5
2
2.5
3
0 0.1 0.2 0.3 0.4 0.5 0.6
logQ
logH

8. Comment:
𝑪 𝒅 Is not constant
But the values of 𝑪 𝒅 should be close to eachother
y = 8.3911x2.8057
R² = 0.9808
0
50
100
150
200
250
300
350
400
0 0.5 1 1.5 2 2.5 3 3.5 4
Q
H
n=2.805
k=8.391

9. 2. Impact of Jet
Objective of the Experiment
To demonstrate and investigate the validity of theoretical expressions for
the calculation of the force exerted by a jet on objects of various shapes
Theory
From momentum principle
𝐹y = ρQ(vout − vin) , in our case 𝜃 =90 flat plate (90)
Then 𝑣 𝑜𝑢𝑡 = 0
Then 𝐹y = ρQvin force of water on plate ,
vin = vnozzle =
Q
A
, A =
π∗(0.8)2
4
= 0.50265cm2
, 𝐹y = ρ
Q2
A
,
𝑀 = ρ
Q2
gA
Experimental Setup
1. The impact of jet apparatus is placed above the regular Hydraulic
Bench as shown in the photographs.
2. A stopwatches.

10. Procedures and Readings
1. Remove the stop plate and transparent casing to measure the nozzle
diameter and place the
flat plate (90º) on the rod attached to the weight pan. Then, reassemble
the apparatus.
2. Connect the inlet pipe of the apparatus to the outlet of the Hydraulic
Bench.
3. Level the base of the apparatus using the bubble balance.
4. Screw down the top plate to datum on the spirit level.
5. Adjust the level gauge to suit datum on the weight pan.
6. Add masses to the weight pan. Allow water to flow in the experiment
and adjust the flow
by the controlvalve of the Hydraulic Bench so that the pan will be re-
adjacent to the level
gauge.
7. Before taking readings the weight pan should be oscillated upwards
and downwards and
rotated to minimize the effect of friction.
8. Take the readings of the initial and final volumes and the time of
accumulation.
9. Record the masses on the weight pan.
10. Repeat the experiment for different masses on the weight pan
Reading Mass
on
weight
pan M
(gm)
Initial
volume
(I.V.)
(litre)
Final
volume
(F.V.)
(litre)
Time(T)
(Sec)
1 110 1 6 34
2 190 1 6 28

11. 3 210 1 6 22
4 330 1 6 16
5 640 1 6 11
coefficient
of impact
theoretical
mass
Mass
on
weight
pan M
(gm)
Volume=
F.V.-I.V
(Liter)
Time
(Sec)
Q=volume/time
(cm3/s)
𝑄2
2.5081021 43.8578644 110 5 34 147.058824 21626.2976
2.938085 64.6679735 190 5 28 178.571429 31887.7551
2.0047459 104.751428 210 5 22 227.272727 51652.8926
1.6662823 198.045669 330 5 16 312.5 97656.25
1.5274255 419.005713 640 5 11 454.545455 206611.57
𝑠𝑙𝑜𝑝𝑒 =
ρ
gA
= 0.00273738
Comment
Coefficient of impact is greater than 1 (in our case)
And the real value of
ρ
gA
= 0.00203 so close to the value of the slope
0
100
200
300
400
500
600
700
0 50000 100000 150000 200000 250000
M
Q^2
slope=0.00273738

12. 3. Flow through Sharp Edged Orifice.
-
Objective of the Experiment
1. To study the path of water jets issuing from orifices.
2. To determine the coefficients of discharge, velocity and contraction
from a sharp-edged circular orifice
.3. To study the variation and dependence of the relevant parameters
Theory
The coefficient of discharge Cd is the ratio of the actual discharge Q act
to the theoretical discharge Qth.
The theoretical discharge is given by the following relationship where A
is the area of the orifice and H
is the total head on the orifice centerline and the actual discharge can be
measured.
𝑄𝑡ℎ = 𝐴√2𝑔𝐻 𝐶𝑑 =
𝑄 𝑎𝑐𝑡
𝑄𝑡ℎ
< 1
The Path of the jet from the orifice is given by the following equation
where x is the horizontal distance, y is the vertical distance and v is the
flow velocity from the orifice
𝑋 = 𝑉𝑎𝑐𝑡 𝑡. 𝑦 = 0.5𝑔𝑡2
𝑦 = 0.5𝑔
𝑥2
𝑣 𝑎𝑐𝑡
2
from bernolli 𝑣𝑡ℎ = √2𝑔𝐻
𝑦 = 0.5𝑔
𝑥2
𝑐 𝑣
22𝑔𝐻
𝐶 𝑉 =
𝑋
2√ 𝑦 ∗ 𝐻
Experimental setup
1. The orifice plate apparatus is placed above the regular Hydraulic
Bench as shown in the photographs.
2. A stopwatchis needed.
3. The adjustable stainless steel overflow pipe near the top of the tank is
used to adjust the level of water in the tank
.
.

13. Procedures and Readings
1. Turn on the pump of the hydraulic bench and allow water into the
constant head tank to build up above the orifice. Wait until steady
condition is achieved
2. You can control the level of the water into the constant head tank by
pulling up and down the adjustable stainless steel overflow pipe as shown
in the photograph.
3. Measure the head (H) above the orifice using the graduated scale.
4. By setting the thin pins so that they just touch the issuing water jet,
draw the path of the water jet on the given graph paper.
5. Measure and record the initial and final volumes and the time of
accumulation for each reading of head (H).
6. Repeat the previous steps for at least four more different heads (H) by
changing the position of the adjustable stainless steel overflow pipe.

14. Point 1 Point 2 Point 3 Point 4 Point 5 Point 6 H(c
m)
Initial
volum
Final
volum
v Time
X
(cm)
5 10 15 20 25 30 33.5 4 10 6 2.6
min
Y
(cm)
0.2 0.7 1.6 3 4.7 7.2
X2 25 100 225 400 625 900
𝐶 𝑣=
(x2 /
4yH).5
0.96584 1.03252 1.02441 0.9975 0.9961 0.9658
𝑉𝑡ℎ = √2𝑔𝐻 = 256.372 𝑐𝑚 𝑠𝑒𝑐⁄
𝑄𝑡ℎ = 𝐴𝑉𝑡ℎ = 72.48𝑐𝑚3
𝑠𝑒𝑐⁄ , 𝐴 = 𝜋
0.62
4
= 0.282743 𝑐𝑚2
𝑄 𝑎𝑐𝑡 =
6 ∗ 1000
156
= 38.46 𝑐𝑚3
𝑠𝑒𝑐⁄
𝐶𝑑 =
38.46
72.48
= 0.530
the normal range should be between (0.6-0.9)
Slope=4H𝑪 𝒗
𝟐
=128.4
𝑪 𝑽=0.9788814
𝐶𝑐 =
𝐶𝑑
𝐶𝑣
=
0.530
𝟎. 𝟗𝟕𝟖𝟖𝟖𝟏𝟒
= 0.54143
y = 128.4x
R² = 0.996
0
100
200
300
400
500
600
700
800
900
1000
0 1 2 3 4 5 6 7 8
X^2
Y

15. Point 1 Point 2 Point 3 Point 4 Point 5 Point 6 H(c
m)
Initial
volum
e
Final
volum
e
v Time
(sec)
X
(cm)
0 5 10 15 20 25
36.4
7 9 2 72.7
Y
(cm)
0 0.5 1.1 2.7 4 6.15
X2 0 25 100 225 400 625
𝐶 𝑣=
(x2 /
4yH).5
0 1.172018 1.580349 1.51306 1.65748 1.67090
𝑉𝑡ℎ = √2𝑔𝐻 = 267.239 𝑐𝑚
𝑠𝑒𝑐⁄
𝑄𝑡ℎ = 𝐴𝑉𝑡ℎ = 75.56 , 𝐴 = 𝜋
0.62
4
= 0.282743
𝑄 𝑎𝑐𝑡 =
2 ∗ 1000
72.7
= 27.5𝑐𝑚3
𝑠𝑒𝑐⁄
𝐶𝑑 =
27.5
75.56
= 0.36399
the normal range should be between (0.6-0.9)
𝐶𝑐 =
𝐶𝑑
𝐶𝑣
=
0.36399
0.707854
= 0.5142

16. Point 1 Point 2 Point 3 Point 4 Point 5 Point 6 H(c
m)
Initial
volum
e
Final
volum
e
v Time
X
(cm)
0 5 10 15 20 25
38.9
6 8 2 55.1
Y
(cm)
0 0.5 1 2.6 2.9 5.8
X2 0 25 100 225 400 625
𝐶 𝑣=
(x2 /
4yH).5
0 1.133731
47
1.603338 1.49152
2
1.88302
5
1.66437
𝑉𝑡ℎ = √2𝑔𝐻 = 276.264 𝑐𝑚 𝑠𝑒𝑐⁄
𝑄𝑡ℎ = 𝐴𝑉𝑡ℎ = 78.111 𝑐𝑚3
𝑠𝑒𝑐⁄ , 𝐴 = 𝜋
0.62
4
= 0.282743 𝑐𝑚2
𝑄 𝑎𝑐𝑡 =
2 ∗ 1000
55.11
= 36.291 𝑐𝑚3
𝑠𝑒𝑐⁄
𝐶𝑑 =
36.291
78.111
= 0.4646
the normal range should be between (0.6-0.9)
𝐶𝑐 =
𝐶𝑑
𝐶𝑣
=
0.4646
0.720018
= 0.6452
-100
0
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7
X^2
Y
slope=103.0636
Cv=0.707854

17. 4- Buoyancy Experiment
Objectives of Experiment
1-To verify the waterdensity
2-To calculate the wooddensity
3-To study the effectof C.G locationon the stability condition
Theory
 𝑭 𝑩 = 𝜸 𝒇*∀ 𝒅𝒊𝒔𝒑
 MG=
𝑰 𝒎𝒊𝒏
∀ 𝒅𝒊𝒔𝒑
− 𝑮𝑩
Where
𝑭 𝑩= Buoyant force
𝜸 𝒇 = Specific weightof fluid
∀ 𝒅𝒊𝒔𝒑
𝑴𝑮
= Fluid volume displaced by body / Distance from metacenter to
center of gravity of body
𝑰 𝒎𝒊𝒏
𝑮𝑩
= Minimum moment of inertia of the fluid line area of the body /
Distance from center of gravity to center
-100
0
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7
X^2
Y
slope=112.0349
Cv=0.720018

18. Procedures
1-Make sure that the nut is put at lowestposition
2-put the model on watersurface
3-waituntil water disturbance disappearmeasure the depth of
submergence by attachedruler on the model
4-Add weights to the screw and wait while then measure the depth of
submergence
5-Repeatstep4more than one time and measure the depth of
submergence
Reading weight added ( gm) depth of submergence (mm)
1 0 54.4
2 10 55.5
3 20 56.5
4 40 58.57
5 50 59.6
reading weight
added (gm)
depth of
submergence
(mm)
volume
initial (m^3)
volume final
(m^3)
volume
(m^3)
Totalweight
(N)
Ɣ fluid
(Nm^3)
1 0 54.5 0.000214 0 0.000214 1.82466 6876.17
2 10 55.5 0.000214 0.000012 0.000226 1.92276 6945.13
3 20 56.5 0.000214 0.000024 0.000236 2.02086 7066.53
4 40 58.5 0.000214 0.000036 0.000254 2.6611 7338.188
5 50 59.5 0.000214 0.00006 0.000274 2.31516 7160.58

19. Slope = 𝜸 water=8941.5 𝑵 𝒎 𝟑⁄ =894.15 𝒌𝒈 𝒎 𝟑⁄
Comment:
Gama water is not accurate because there is an error in reading or
problem in
Must be 1000 kg m3⁄ or 9810 𝑁 𝑚3⁄
PART II
Procedures
1- Make the nutat certain position
2- Calculate the total volume of the wooden body
3-Putthe model on water surface
4-Wait until water disturbancedisappear and measure the depth of
submergence
5-Calculate the submerged volume
6-Calculate the specific weight of wood by Archimedes law.
y = 8941.5x
R² = 0.577
0
0.5
1
1.5
2
2.5
3
0 0.00005 0.0001 0.00015 0.0002 0.00025 0.0003
Weight(gm)
∆ Volume (m^3)

20.  𝛾 𝑤𝑜𝑜𝑑 ∗ ∀ 𝑡𝑜𝑡𝑎𝑙 +𝑊𝑛𝑢𝑡 + 𝑊𝑠𝑐𝑟𝑒𝑤 =𝛾 𝑤𝑎𝑡𝑒𝑟 ∗ ∀ 𝑠𝑢𝑏𝑚𝑒𝑟𝑔𝑒𝑑
𝛾 𝑤𝑜𝑜𝑑(𝑎𝑐𝑡𝑢𝑎𝑙) = 𝑊 𝑉⁄ = 0.173 ( 4∗ 10−4⁄ ) =432.5 𝑘𝑔 𝑚3⁄
𝛾 𝑤𝑜𝑜𝑑(𝑡ℎ) = (894.15 ∗ 2.14 ∗ 10−4
− 0.063) (4 ∗ 10−4⁄ )
= 320.870 𝑘𝑔 𝑚3⁄
Comment:
There is an error in (𝛾 𝑤𝑜𝑜𝑑) because there is an error in (𝛾 𝑤𝑎𝑡𝑒𝑟 ) from
error in reading
PART III
Procedures
1-Makethe nut at certain position and measurethe height of the C.G. of
nut w .r.twooden body upper surface
2-Pat50 gm weight specie on the nut measurethe height of C.G. of
weight specie w.r.t. wooden body upper surface
3-Putthe model on water surface
4-Observeif the model is stable or un stable
5-Record the height of each trial and the status obtained stable,
unstable
6-Calculate the required height of 50 gm weight specie to reach the
neutral case and compareit with observed height
 MG=
𝐼 𝑚𝑖𝑛
𝑉𝑠𝑢𝑝
− 𝐵𝐺
When it in natural case MG= 0 we add 50 gm
𝐼 𝑚𝑖𝑛 = 6.4*10−6
𝑚4
V=2.68*10−4
BG=OG-OB

21. BG= 59.73-36.9=22.83 mm
𝐼 𝑚𝑖𝑛
𝑉
=
6.4∗10−6
2.68∗10−4
=0.02888 m= 23.88 mm
Comment:
The bodywas stable just before turned over cannot calculated in lap
cause error in reading.