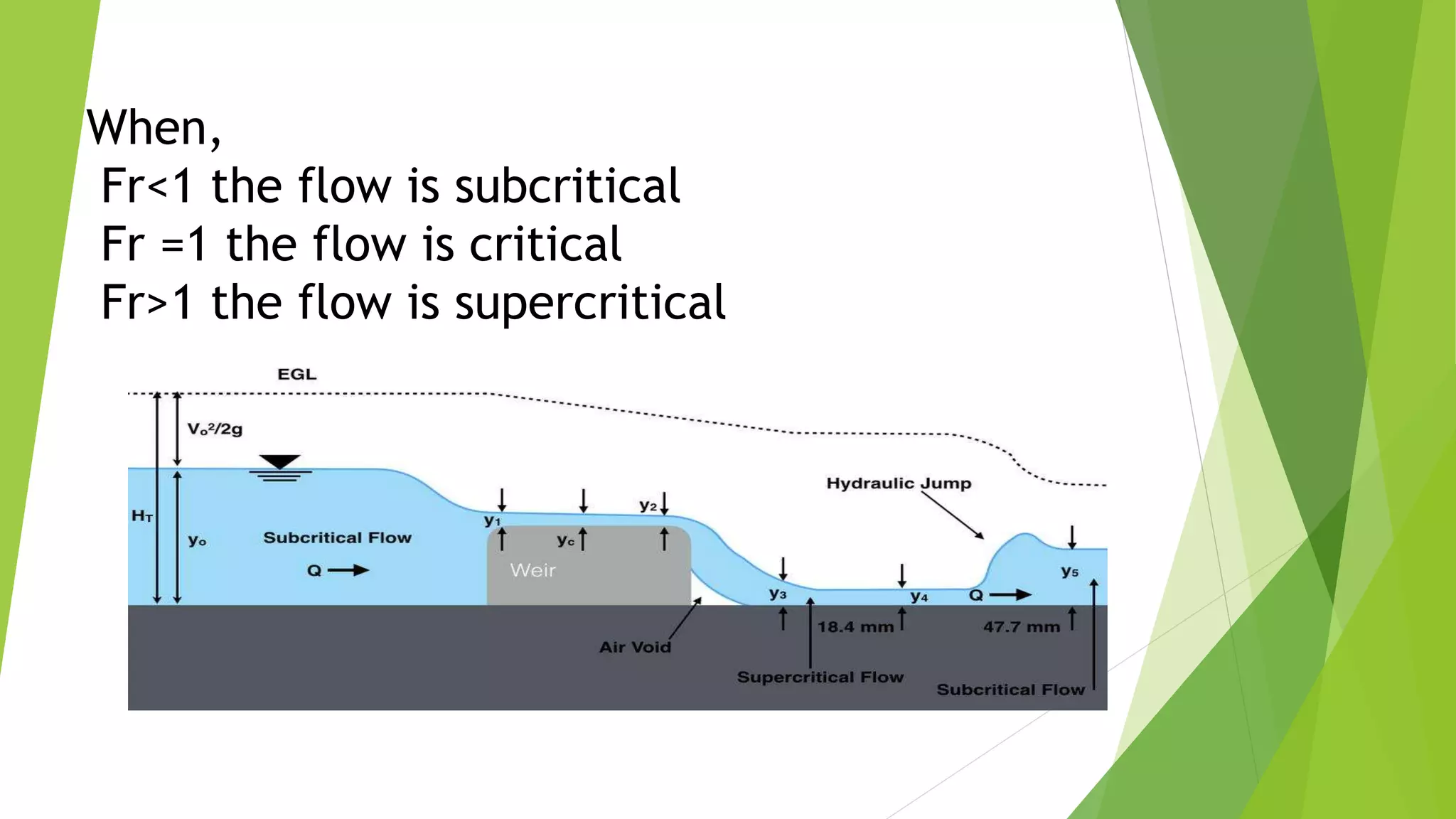
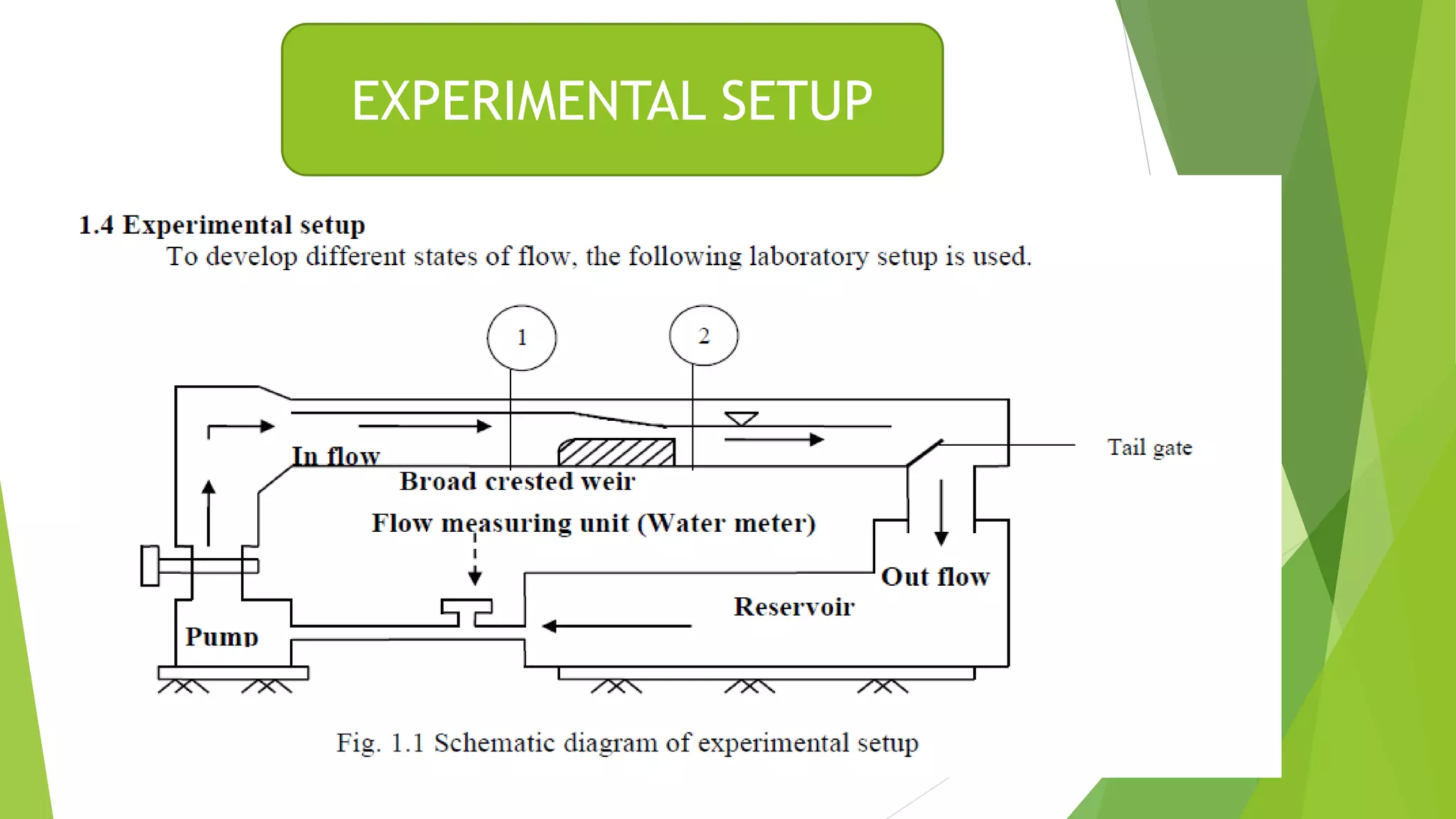
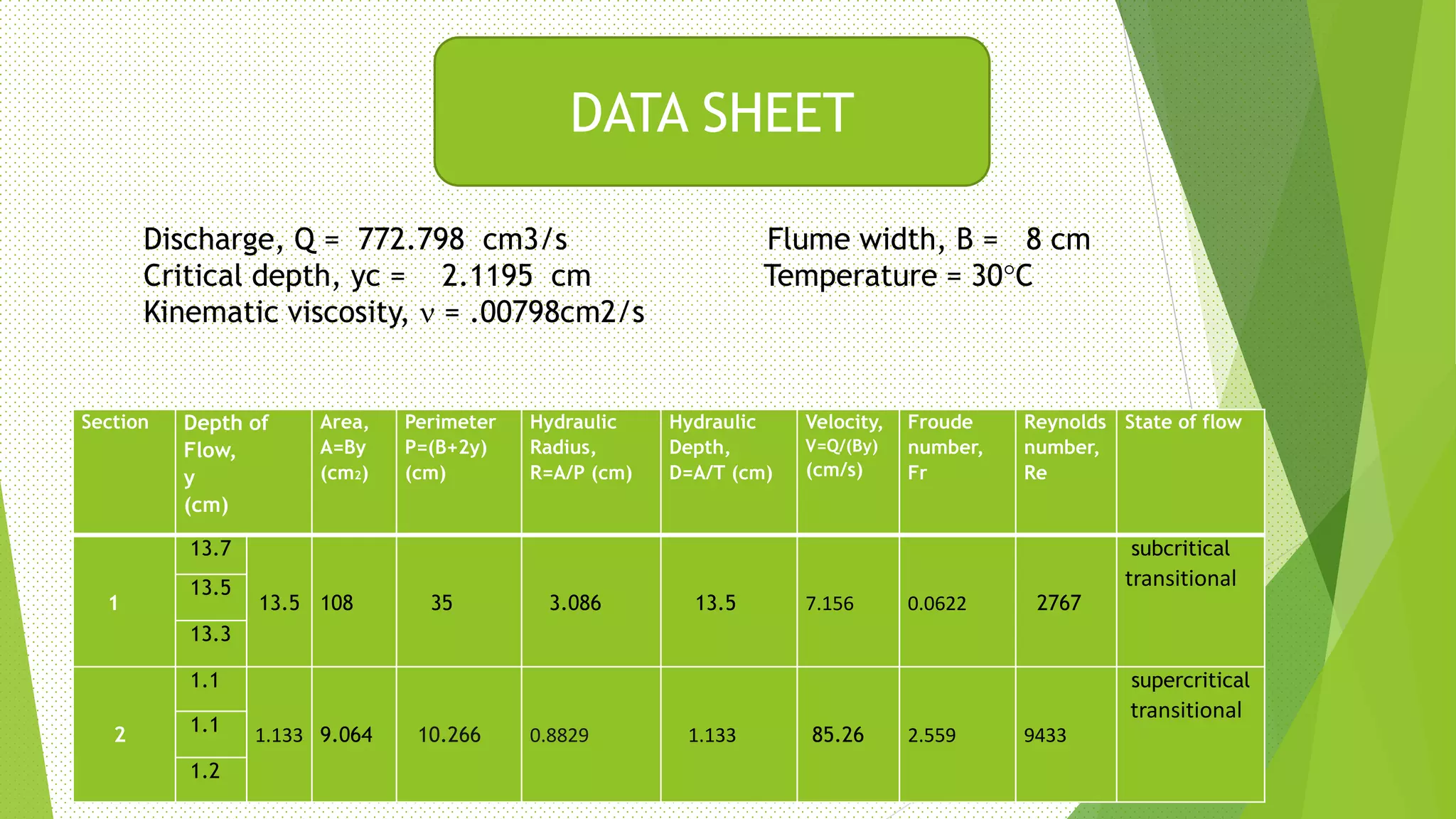
The document summarizes an experiment on determining the state of open channel flow. It includes the background, objectives to determine flow state, critical depth, and Reynolds and Froude numbers. The experimental setup used a flume and point gauge to measure depth upstream and downstream of a weir. Flow was found to be subcritical transitional at section 1 and supercritical transitional at section 2, based on calculated Reynolds and Froude numbers. The critical depth was also calculated.

1. CourseNo.:CE-3202
Credit:0.75
CourseTitle:Openchannelflowsessional
DHAKAUNIVERSITY OF ENGINEERING & TECHNOLOGY, GAZIPUR

2. WELCOME
Presentation
on
Determination of state of flow and
critical depth in an open channel
To

3. Presented
to:
Dr. Mohammad Alauddin
Professor
Dept. of CE
DUET
Ms. Rokshana Pervin
Asst.-Professor
Dept. of CE
DUET

4. GROUP NO. 01
1. MD MEHEDI HASAN
2. MD MOMIN ALI
3. MD RABEUL AWAL
4. MEHEDI HASAN SHAMIM
5. HELAL SARKER
6. M M ALAMGIR HOSSAIN
7. FAYSAL AHAMED
8. MORSHEDUL ALAM
9. EKRAMUL TALUKDER
10. S.M. SHAHEDUR RAHMAN
161065
161067
161068
161069
161071
161072
161073
161074
161075
161076
PRESENTED BY

5.  Background
 Objectives
 Theory
 Experimental setup
 Procedure
 Data sheet
 References
CONTENT

6. The state of open channel flow is mainly
governed by the combined effect of viscous and
gravity forces relative to the inertial forces.
This experiment mainly deals with
determination of the state of flow in an open
channel at a particular section. The state of
flow is very important, as the flow behavior
depends on it. In order to construct different
structures in rivers and canals and to predict
the river response, the state of flow must be
known. The experiment also deals with
determination of critical depth, which is very
useful in determining the types of flow in
practice.
BACKGROUND

7. 1) To measure water depth both upstream and
downstream of a weir.
2) To determine the Reynolds number (Re) and the
Froude number (Fr).
3) To determine the state of flow.
4) To determine critical depth (yc).
5) To observe the subcritical and the supercritical flows.
OBJECTIVES

8. Depending on the effect of viscosity relative to inertia,
the flow may be laminar, turbulent or transitional. The
effect of viscosity relative to the inertia is expressed by
the Reynolds number, given by
Re =
𝑉𝑅
𝑣
THEORY
V = The mean velocity of flow,
R = The hydraulic radius =A/P
A =The wetted cross-sectional area,
P = The wetted perimeter and
 = The kinematic viscosity of water.

9. When,
Re <500 the flow is laminar.
500  Re 12,500 the flow is transitional.
Re > 12,500 the flow is turbulent.

10. When the flow is dominated by the gravity, then the
type of flow can be identified by a dimensionless
number, known as Froude Number, given by
Fr =
𝑉
𝑔𝐷
V = the mean velocity of flow,
D = the hydraulic depth (= A/T),
A = the cross-sectional area,
T = the top width and
g =The acceleration due to
gravity

11. When,
Fr<1 the flow is subcritical
Fr =1 the flow is critical
Fr>1 the flow is supercritical

12. Depending on the numerical values of
Reynolds and Froude numbers, the following
four states of flow are possible in an open
channel:
i) Subcritical laminar Fr<1, Re<500
ii) Supercritical laminar Fr>1, Re<500
iii) Subcritical turbulent Fr<1, Re>12,500
iv) Supercritical turbulent Fr>1, Re>12,500

13. DETERMINATION OF STATE OF FLOW WITHOUT
ANY MEASUREMENT

14. Critical depth
Flow in an open channel is critical when the Froude
number of the flow is equal to unity. Critical flow in a
channel depends on the discharge and the geometry of
channel section. For a rectangular section, the critical
depth is given by
yc=
3 𝑄2
𝑔𝐵2
Where,
yc = The critical depth,
Q = The discharge and
B = The width of the channel.

15. EXPERIMENTAL SETUP

16. i) The depth of flow is measured at sections 1 and 2 by
a point gage.
ii) The reading of discharge is taken.
iii) The velocity at both the sections is calculated.
iv) Re and Fr for the both sections are calculated by
using the equations of Re and Fr. It helps us to
determine the state of flow.
v) The critical depth yc is calculated by using the
equation of critical depth.
PROCEDURE

17. Discharge, Q = 772.798 cm3/s Flume width, B = 8 cm
Critical depth, yc = 2.1195 cm Temperature = 30C
Kinematic viscosity,  = .00798cm2/s
DATA SHEET
Section Depth of
Flow,
y
(cm)
Area,
A=By
(cm2)
Perimeter
P=(B+2y)
(cm)
Hydraulic
Radius,
R=A/P (cm)
Hydraulic
Depth,
D=A/T (cm)
Velocity,
V=Q/(By)
(cm/s)
Froude
number,
Fr
Reynolds
number,
Re
State of flow
1
13.7
13.5 108 35 3.086 13.5 7.156 0.0622 2767
subcritical
transitional13.5
13.3
2
1.1
1.133 9.064 10.266 0.8829 1.133 85.26 2.559 9433
supercritical
transitional
1.1
1.2

18. • www.google.com
• www.wikipedia.com
• www.britannica.com
• www.engineersedge.com
REFERENCES

19. ANYQUERY