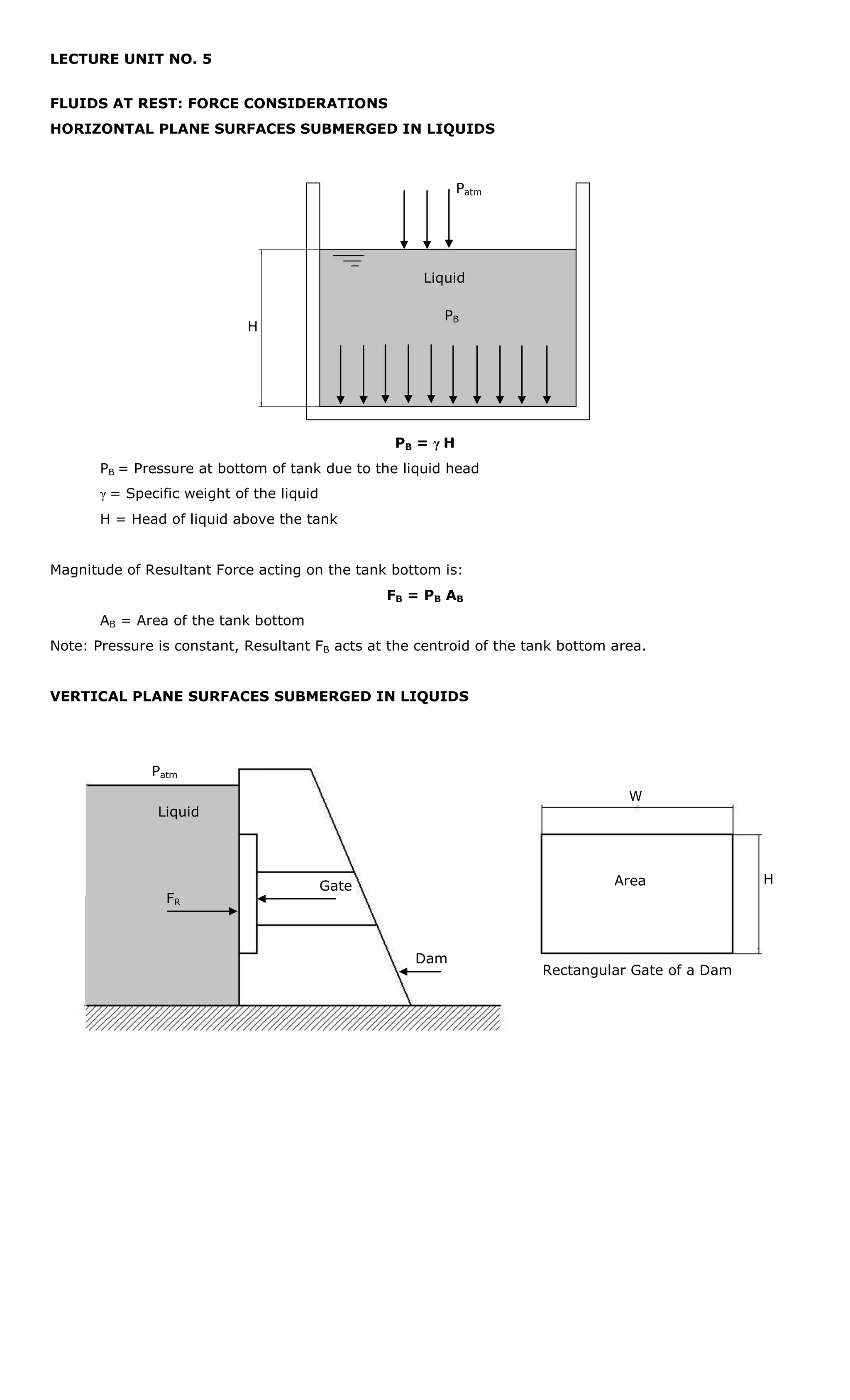
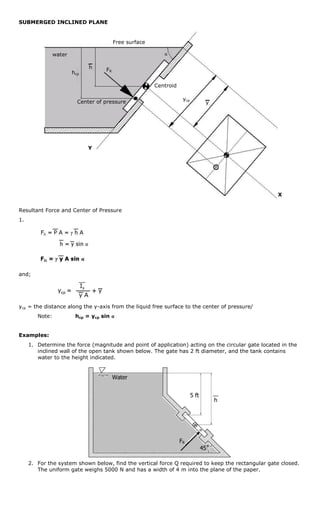
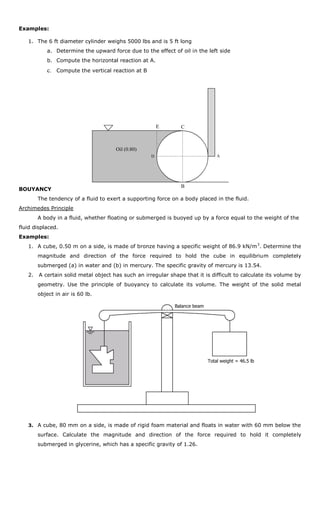
1. The document discusses hydrostatic forces on submerged surfaces including horizontal, vertical, and inclined planes as well as curved surfaces. 2. Key concepts include calculating hydrostatic force based on pressure, depth, and surface area. The center of pressure is also introduced, which is where the total hydrostatic force acts rather than at the geometric centroid. 3. Example problems are provided to calculate hydrostatic forces, center of pressure locations, and buoyancy forces on various submerged objects.

1. LECTURE UNIT NO. 5
FLUIDS AT REST: FORCE CONSIDERATIONS
HORIZONTAL PLANE SURFACES SUBMERGED IN LIQUIDS
Patm
Liquid
PB
H
PB = γ H
PB = Pressure at bottom of tank due to the liquid head
γ = Specific weight of the liquid
H = Head of liquid above the tank
Magnitude of Resultant Force acting on the tank bottom is:
FB = P B A B
AB = Area of the tank bottom
Note: Pressure is constant, Resultant FB acts at the centroid of the tank bottom area.
VERTICAL PLANE SURFACES SUBMERGED IN LIQUIDS
Patm
W
Liquid
Gate Area H
FR
Dam
Rectangular Gate of a Dam

2. hcp h
Centroid H
Pressure
Intensity Line
Center of Pressure
W
FR = γ h A = P A
γ = Specific weight of liquid
h = depth of the centroid of gate area
A = Area of gate
P = Pressure at centroid of gate area
FR = Resultant force on gate area / Hydrostatic force on the gate
Center of Pressure
Since the pressure acting on submerged vertical area is not uniform (not constant), the resultant
force does not act on the centroid of the gate area. The resultant force act on another point called Center
of Pressure.
IX = Centroidal moment of inertia of plane surface About the X-Axis
h = depth to centroid of plane
A = Area of plane surface
hcp = depth to center of pressure
The greater the depth of the plane surface, the smaller the distance between the centroid and center of
pressure.
Vertical distance between the center of pressure and the centroid.

3. SUBMERGED INCLINED PLANE
Free surface
water α
h FR
hcp
Centroid
ycp
Center of pressure y
Y
X
Resultant Force and Center of Pressure
1.
and;
ycp = the distance along the y-axis from the liquid free surface to the center of pressure/
Note: hcp = ycp sin α
Examples:
1. Determine the force (magnitude and point of application) acting on the circular gate located in the
inclined wall of the open tank shown below. The gate has 2 ft diameter, and the tank contains
water to the height indicated.
Water
5 ft
h
FR
45˚
2. For the system shown below, find the vertical force Q required to keep the rectangular gate closed.
The uniform gate weighs 5000 N and has a width of 4 m into the plane of the paper.

4. Hinge
6m
5000 N
3m
Q cg
cp
FR
60˚
CURVED SURFACES SUBMERGED IN LIQUIDS
- tanks, dams, pipes, gates and reservoir
a. Horizontal Component of Hydrostatic Force
Fh = horizontal component of the hydrostatic pressure is equal to the total pressure on the
projection of that surface on a vertical plane which is normal to the chosen axis.
r
r
The location of Fh is at the center of pressure of the submerged
vertical plane
b. Vertical Component of Hydrostatic Force
Fv = vertical component of the hydrostatic pressure is equal to the weight of that volume of
water or liquid extending vertically from the surface of the free surface of liquid.
The location of Fv is at the centroid of the liquid inside the quarter-cylinder.
c. Resultant Force

5. Examples:
1. The 6 ft diameter cylinder weighs 5000 lbs and is 5 ft long
a. Determine the upward force due to the effect of oil in the left side
b. Compute the horizontal reaction at A.
c. Compute the vertical reaction at B
E C
Oil (0.80)
D A
B
BOUYANCY
The tendency of a fluid to exert a supporting force on a body placed in the fluid.
Archimedes Principle
A body in a fluid, whether floating or submerged is buoyed up by a force equal to the weight of the
fluid displaced.
Examples:
1. A cube, 0.50 m on a side, is made of bronze having a specific weight of 86.9 kN/m 3. Determine the
magnitude and direction of the force required to hold the cube in equilibrium completely
submerged (a) in water and (b) in mercury. The specific gravity of mercury is 13.54.
2. A certain solid metal object has such an irregular shape that it is difficult to calculate its volume by
geometry. Use the principle of buoyancy to calculate its volume. The weight of the solid metal
object in air is 60 lb.
Balance beam
Total weight = 46.5 lb
3. A cube, 80 mm on a side, is made of rigid foam material and floats in water with 60 mm below the
surface. Calculate the magnitude and direction of the force required to hold it completely
submerged in glycerine, which has a specific gravity of 1.26.

6. ---------------------------------------------------------------------------------------------------------------------
PROBLEMS:
1. (a) Compute the depth of the center of pressure for a vertical semi-circular gate of diameter “d”
and radius “r” which is submerged in a liquid and has its diameter on the liquid surface (b)
Compute the location of the center of pressure if the top of the gate is 2 m from the surface and
the radius 2 m. (c) Compute also the total hydrostatic force on one side.
2. A triangular gate 1.20 m base and 1.80 m high is placed on the face of a dam as shown in the
figure. Its bases is hinged and the vertex is attached to a cylindrical buoy whose weight is 440 N.
The external diameter of the buoy is 1.2 m and the weight of the gate is 880 N. The mechanism is
such that the buoy will open the gate if the water surface will rise higher than 4 m.
a. Compute the hydrostatic force acting normal to the gate
b. Compute the location of the normal force from the hinge of the gate
c. What is the length of the cable when the gate is about to open?
440 N
θ
4m Hinge 3m
1.20 m
880 N
1.80 m
3. From the figure shown, the gate is 1 m wide and is hinged at the bottom of the gate.
0.5 m
Stopper
Water
2m Gate
Submerged
concrete block
Hinge
a. Compute the hydrostatic force acting on the gate.
b. Compute the location of the center of pressure of the gate from the hinged
c. Determine the minimum volume of concrete (unit weight = 23.6 kN/m 3) needed to keep the
gate in closed position.

7. 4. An object having a sp. gr of 0.60 floats in a liquid having a sp. gr. of 0.80.
a. What is the percentage of the volume below the liquid surface to the total volume of the
body?
b. If the volume above the liquid surface is 0.024 m3, what is the weight of the object?
c. What is the load that will cause the object to be fully submerged?
5. A board weighing 30 N/m has a cross sectional area of 0.005 m 2 and a length of 3.4 m placed in
the tank of oil having a specific gravity of 0.85. Assuming the hinged to be frictionless
a. Compute the specific gravity of the board
b. Compute the length of the board which is submerged in oil
c. Compute the angle θ for equilibrium conditions
A
θ
1.5
Oil (0.85)
Properties Sections