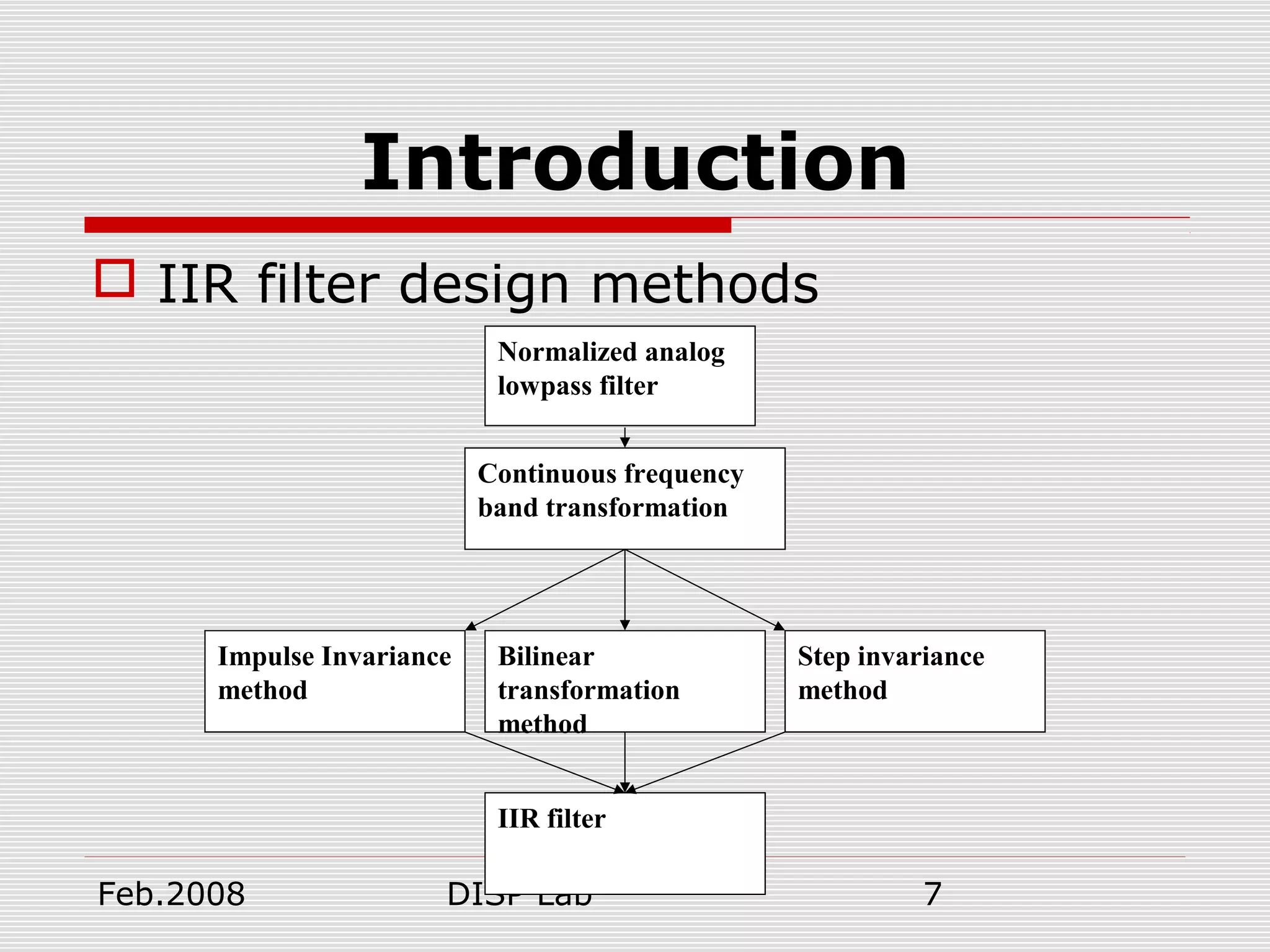
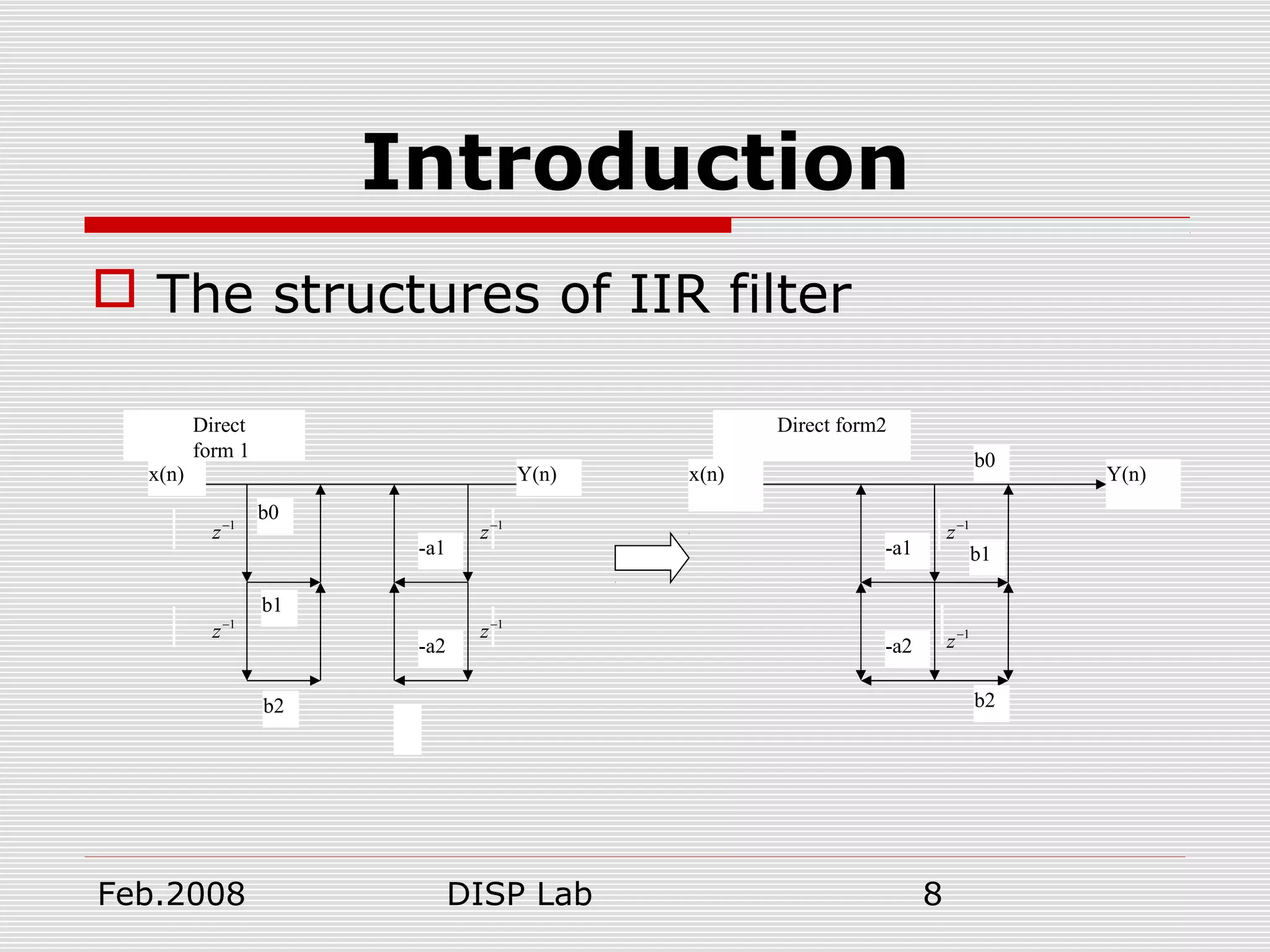
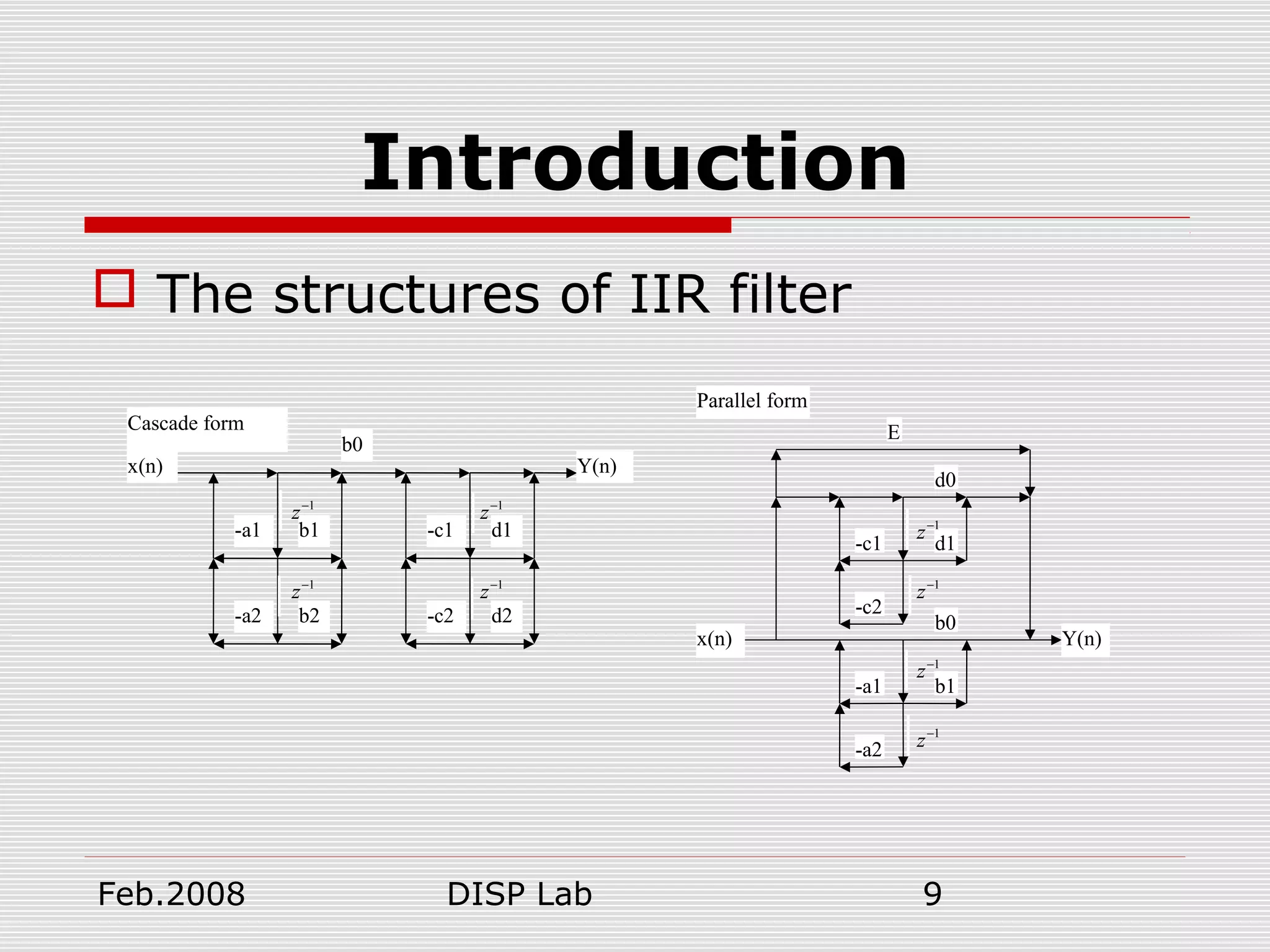
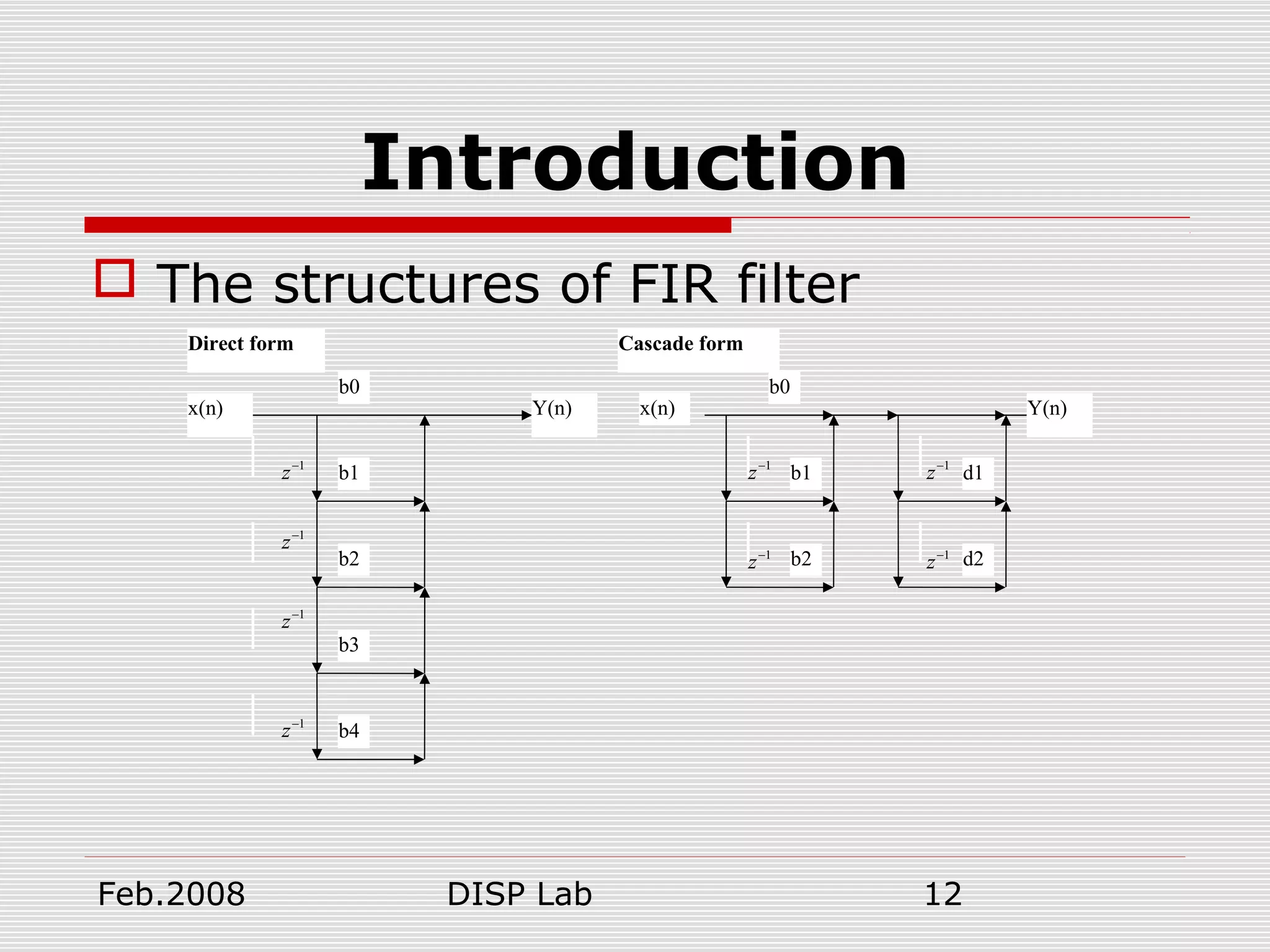
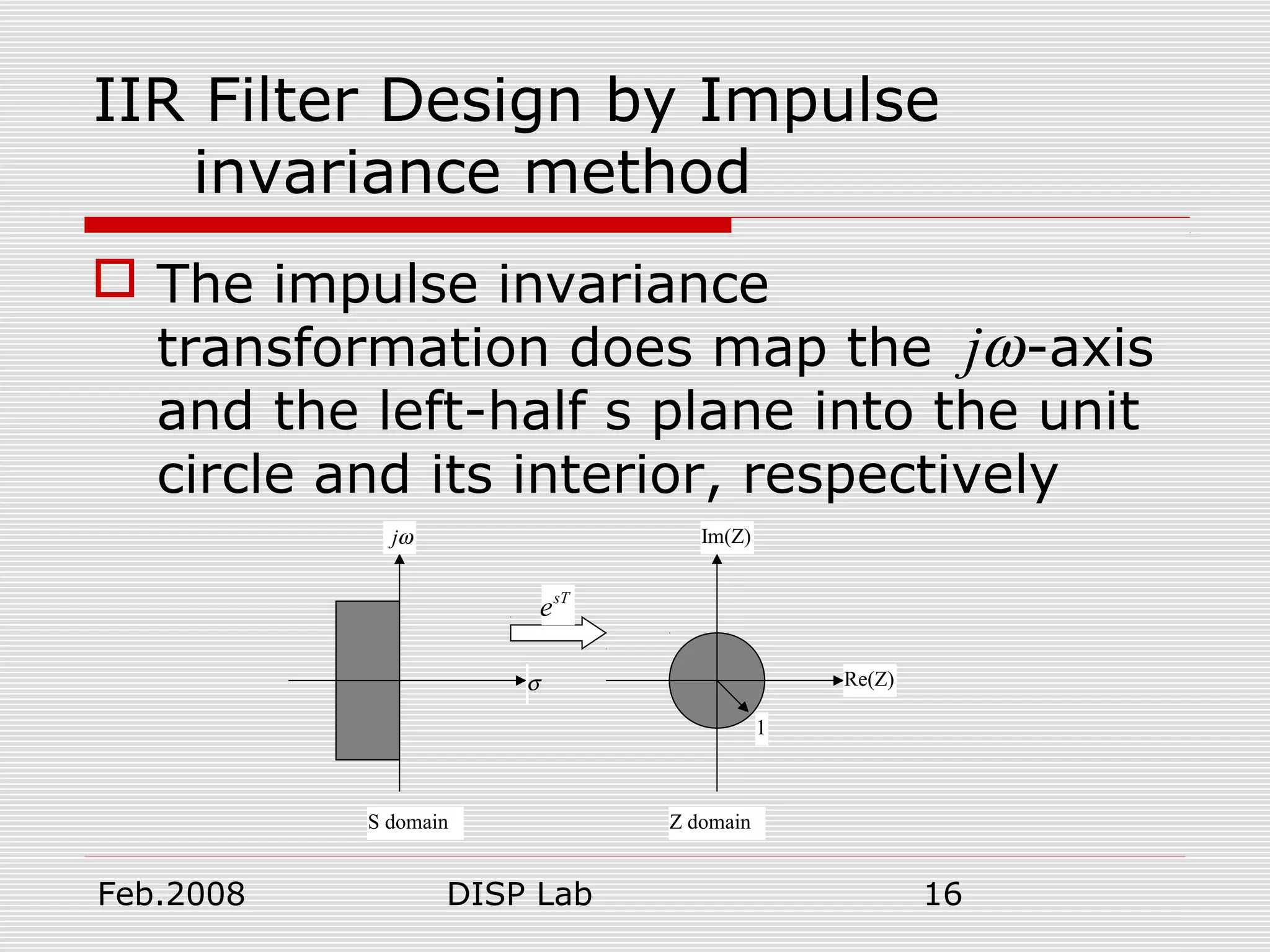
This document summarizes a presentation on FIR and IIR filter design techniques. It introduces common IIR filter design methods like impulse invariance and bilinear transformation. It also discusses FIR filter design using window functions, frequency sampling, and minimizing mean squared error. Specific window functions are examined, including rectangular, triangular, Hanning, Hamming, Kaiser, and Blackman windows. The document provides an overview of digital filter design topics and serves as a reference for further exploration of FIR and IIR filter design methods.





















![Feb.2008 DISP Lab 27
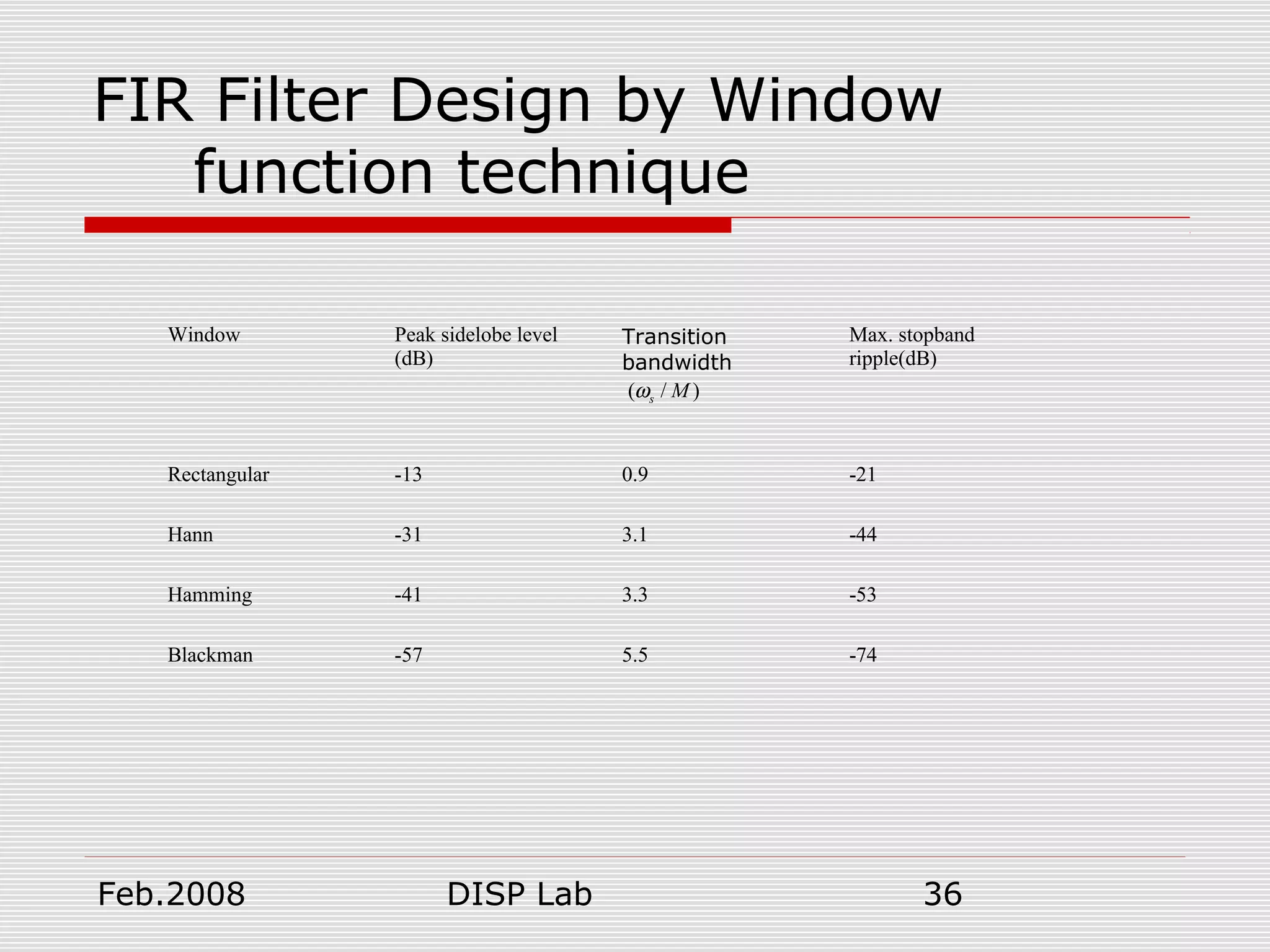
FIR Filter Design by Window
function technique
Simplest FIR the filter design is
window function technique
A supposition ideal frequency
response may express
where
( ) [ ]j j n
d d
n
H e h n eω ω
∞
−
=−∞
= ∑
1
[ ] ( )
2
j j n
d dh n H e e d
π
ω ω
π
ω
π −
= ∫](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-27-2048.jpg)
![Feb.2008 DISP Lab 28
FIR Filter Design by Window
function technique
To get this kind of systematic causal
FIR to be approximate, the most
direct method intercepts its ideal
impulse response!
[ ] [ ] [ ]dh n w n h n= g
( ) ( ) ( )dH W Hω ω ω= ∗](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-28-2048.jpg)

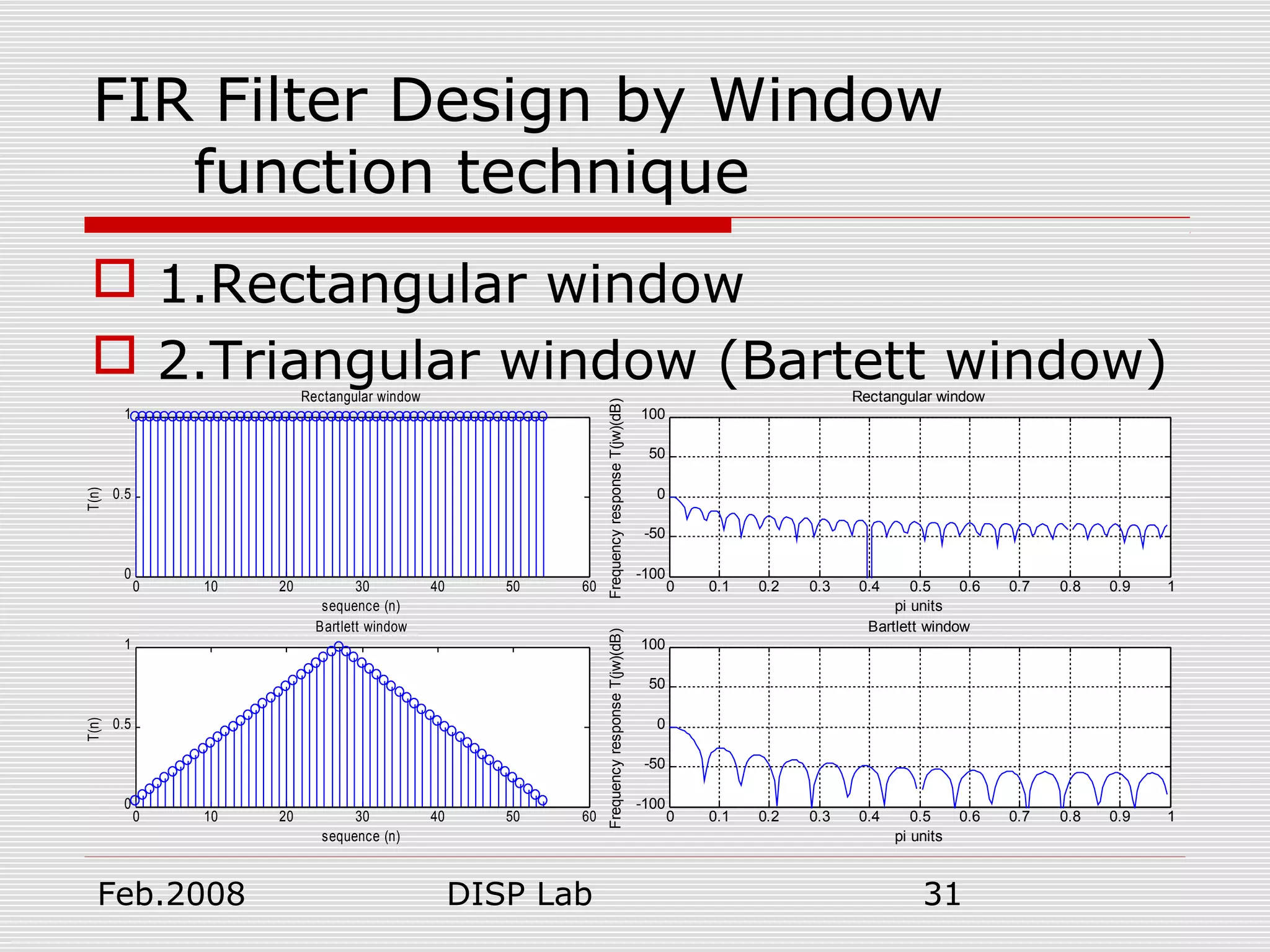
![Feb.2008 DISP Lab 30
FIR Filter Design by Window
function technique
1.Rectangular window
2.Triangular window (Bartett window)
1, 0
[ ]
0,
n M
w n
otherwise
≤ ≤
=
2 , 0
2
2[ ] 2 ,
2
0,
n Mn
M
n Mw n n M
M
otherwise
≤ ≤
= − < ≤
](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-30-2048.jpg)
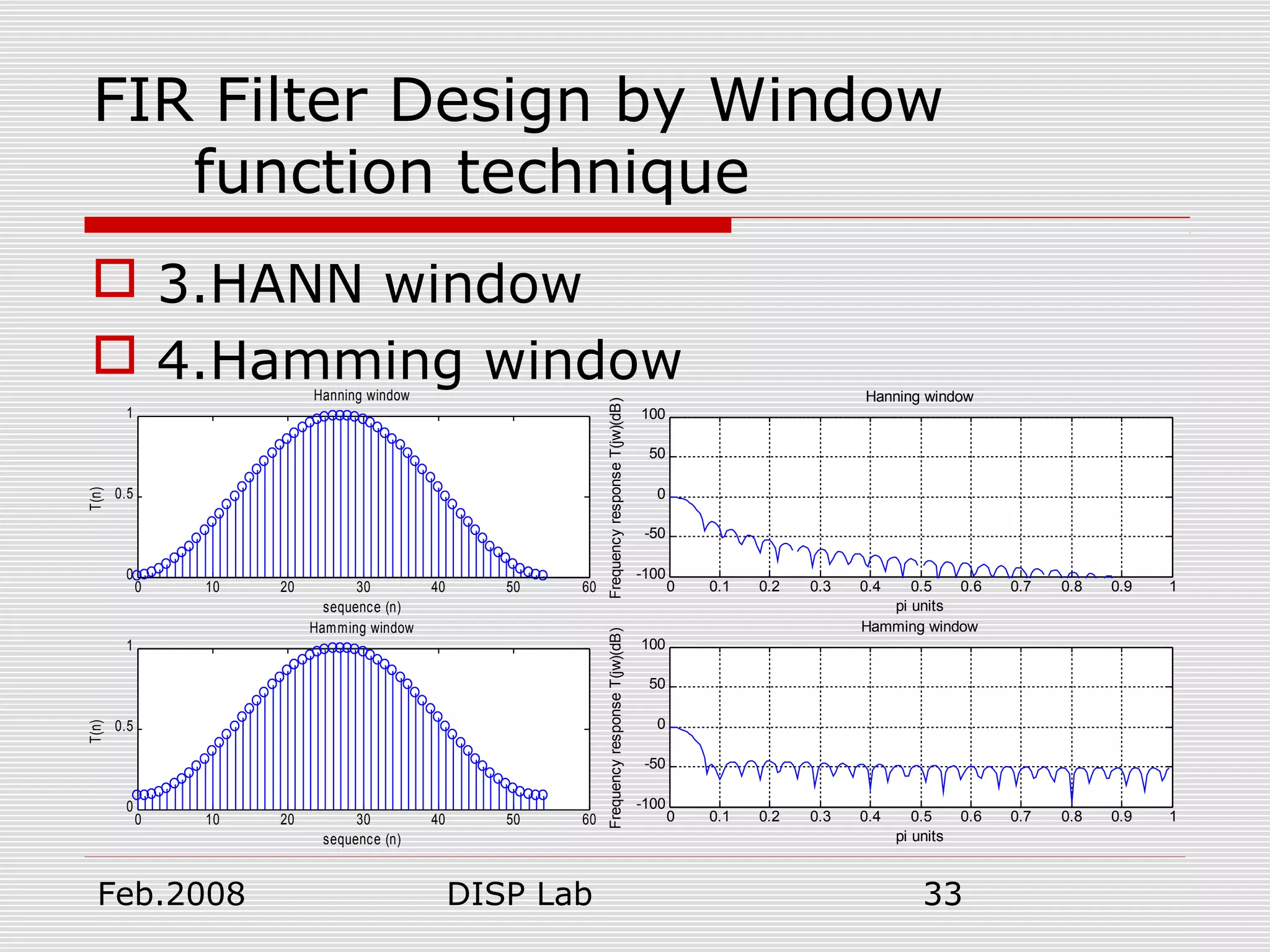
![Feb.2008 DISP Lab 32
FIR Filter Design by Window
function technique
3.HANN window
4.Hamming window
1 2
1 cos , 0
[ ] 2
0,
n
n M
w n M
otherwise
π
− ≤ ≤ =
2
0.54 0.46cos , 0
[ ]
0,
n
n M
w n M
otherwise
π
− ≤ ≤
=
](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-32-2048.jpg)
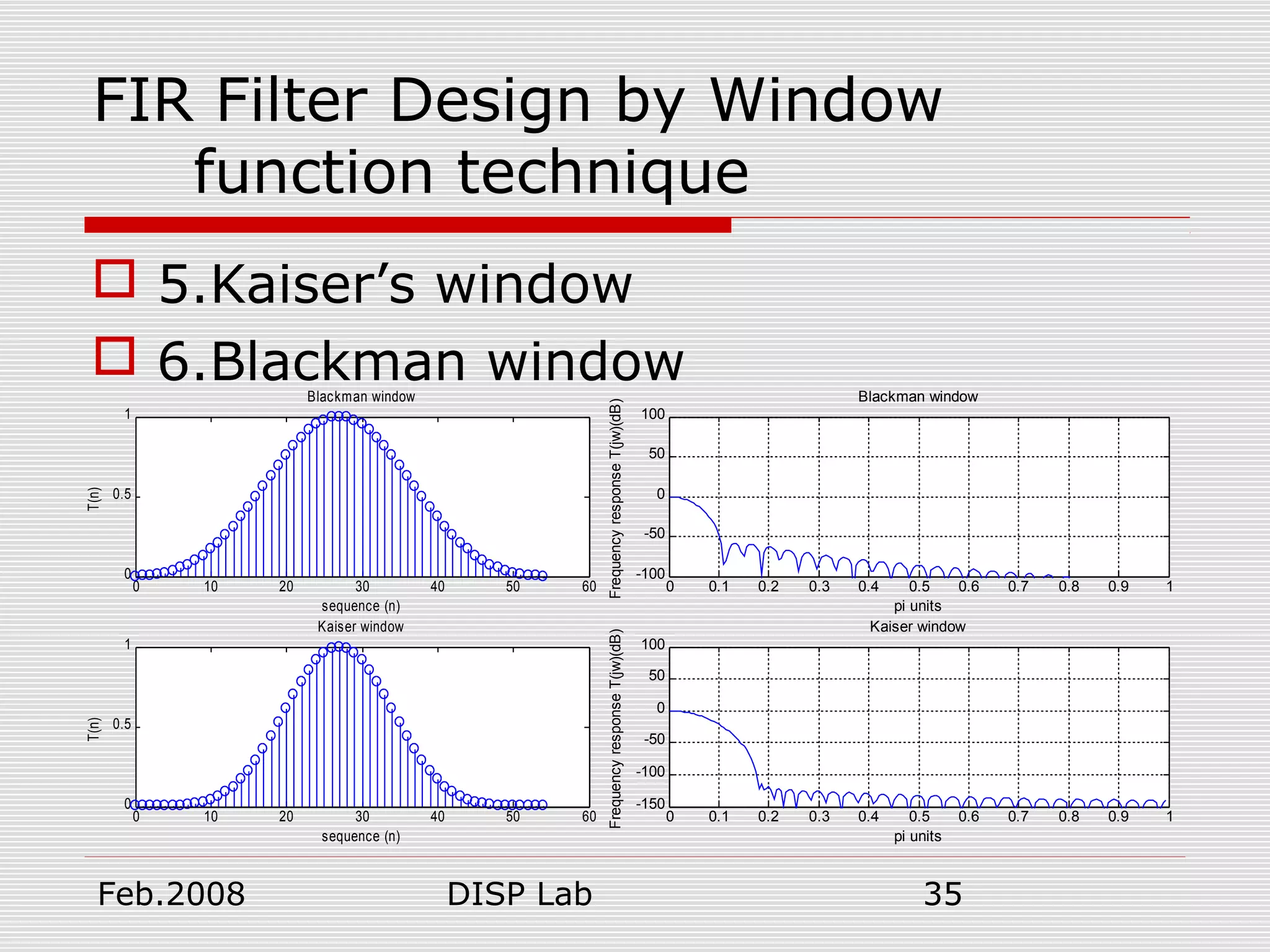
![Feb.2008 DISP Lab 34
FIR Filter Design by Window
function technique
5.Kaiser’s window
6.Blackman window
2
0
0
2
[ 1 (1 ) ]
[ ] , 0,1,...,
[ ]
n
I
Mw n n M
I
β
β
− −
= =
2 4
0.42 0.5cos 0.08cos , 0
[ ]
0,
n n
n M
w n M M
otherwise
π π
− + ≤ ≤
=
](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-34-2048.jpg)

![Feb.2008 DISP Lab 38
FIR Filter Design by Frequency
sampling technique
We wish to derive a linear phase IIR
filter with real nonzero . The
impulse response must be symmetric
where are real and denotes
the integer part
( )h n
[ /2]
0
1
2 ( 1/ 2)
( ) 2 cos( )
1
M
k
k
k n
h n A A
M
π
=
+
= +
+
∑
kA [ / 2]M
0,1,...,n M=](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-38-2048.jpg)

![Feb.2008 DISP Lab 40
FIR Filter Design by Frequency
sampling technique
with corresponding transform
where
Hence
which has a linear phase
1
0
/2
( ) ( )
N
k
k
k N
H z H z
−
=
≠
= ∑
/
2 / 1
(1 )
( )
1
j k N N
k
k j k N
A e z
H z
e z
π
π
−
−
−
=
−
' ( 1)/2 sin / 2
( )
sin[( / / 2)]
j T N
k k
TN
H A e
k N T
ω ω
ω
π ω
− −
=
−](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-40-2048.jpg)
![Feb.2008 DISP Lab 41
FIR Filter Design by Frequency
sampling technique
The magnitude response
which has a maximum value
at where
' sin / 2
( )
sin[( / / 2)]
k k
TN
H A
k N T
ω
ω
π ω
=
−
kN A
/k sk Nω ω= 2 /s Tω π=](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-41-2048.jpg)



![Feb.2008 DISP Lab 45
FIR Filter Design by Frequency
sampling technique
Example: For an ideal lowpass filter
from , we would
choose
The frequency samples are
indeed equal to the desired
' 1, 0,1,...,
( )
0, 1,...,[ / 2]
d k
k P
H
k P M
ω
=
=
= +
'
( ) /k d kA H Nω= ±
( 1) / ( 1), 0,1,...,
0, 1,...,[ / 2]
k
k
M k P
A
k P M
− + =
=
= + '
( )kH ω
'
( )d kH ω](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-45-2048.jpg)

![Feb.2008 DISP Lab 49
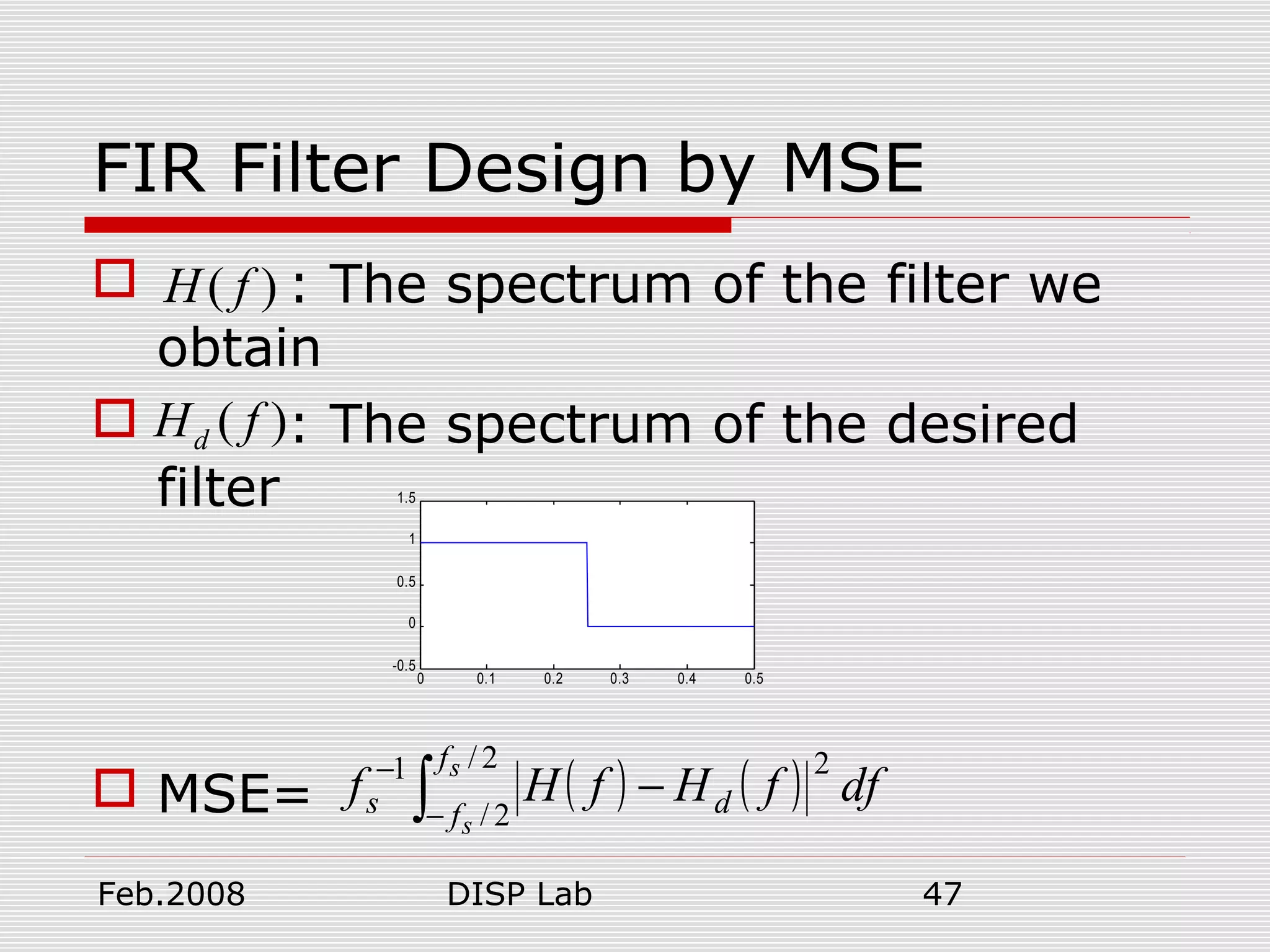
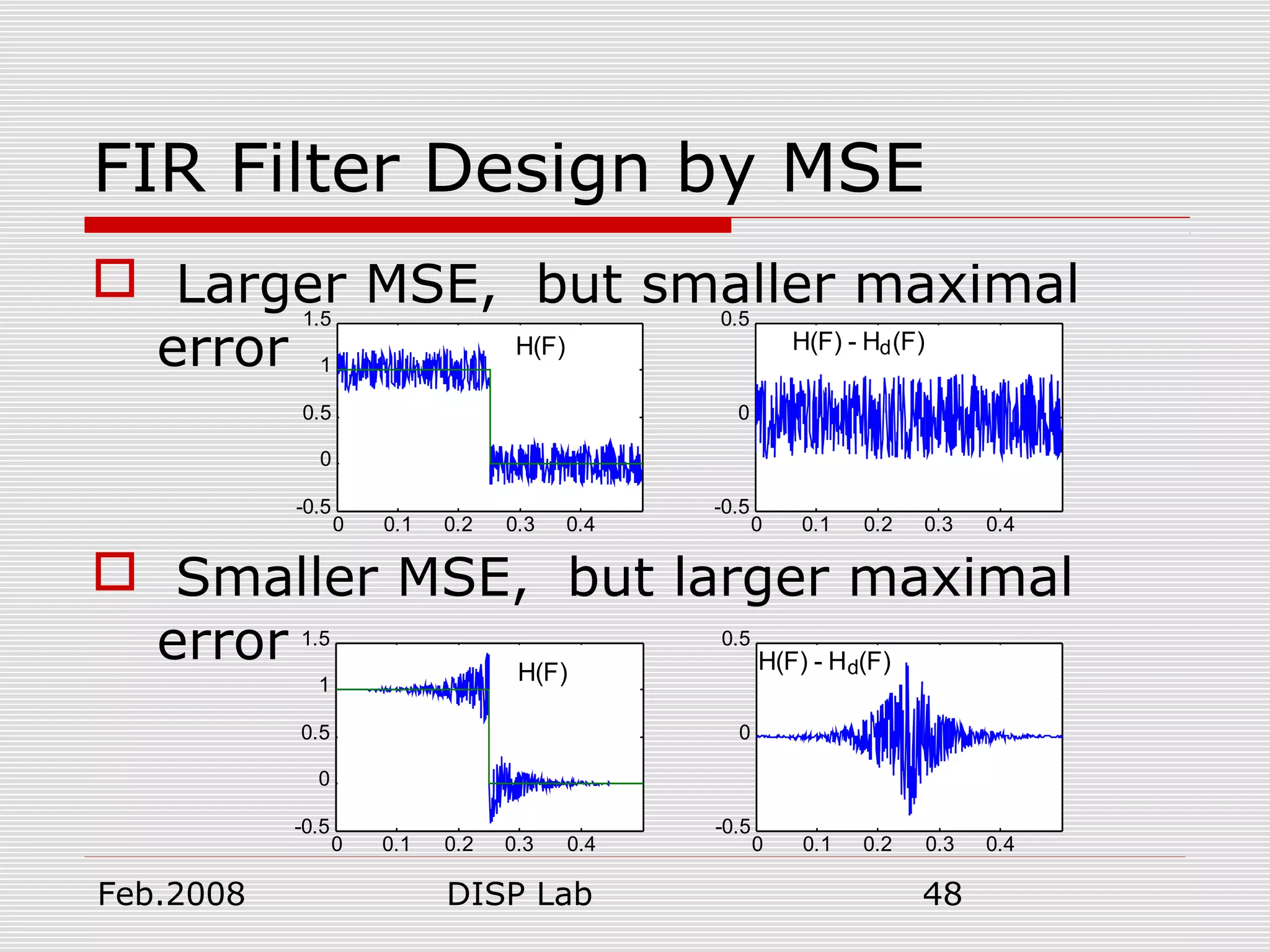
FIR Filter Design by MSE
1. ( ) ( ) ( ) ( )∫∫ −−
−
−=−=
2/1
2/1
22/
2/
21
dFFHFRdffHfRfMSE d
f
f ds
s
s
( ) ( ) dFFHFnns d
k
n
∫ ∑−
=
−=
2/1
2/1
2
0
|| 2cos][ π
( ) ( ) ( ) ( ) dFFHFnnsFHFnns d
k
n
d
k
n
∫ ∑∑−
==
−
−=
2/1
2/1
00
2cos][2cos][ ππ
( ) ( )
1/2
1/2
0 0
[ ]cos 2 [ ]cos 2
k k
n
s n n F s F dF
τ
π τ π τ
−
= =
= ∑ ∑∫
( ) ( ) ( )
1/2 1/2
2
1/2 1/2
0
2 [ ]cos 2
k
d d
n
s n n F H F dF H F dFπ
− −
=
− +∑∫ ∫](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-49-2048.jpg)
![Feb.2008 DISP Lab 50
FIR Filter Design by MSE
2. when n ≠ τ,
when n = τ, n ≠ 0,
when n = τ, n = 0,
3. The formula can be repressed as:
( ) ( ) 02cos2cos
2/1
2/1
=∫−
dFFFn τππ
( ) ( ) 2/12cos2cos
2/1
2/1
=∫−
dFFFn τππ
( ) ( ) 12cos2cos
2/1
2/1
=∫−
dFFFn τππ
( ) ( ) ( )dFFHdFFHFnnsnssMSE dd
k
n
k
n
∫∫ ∑∑ −−
==
+−+=
2/1
2/1
22/1
2/1
01
22
2cos][22/][]0[ π](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-50-2048.jpg)
![Feb.2008 DISP Lab 51
FIR Filter Design by MSE
4. Doing the partial differentiation:
5. Minimize MSE: for all n’s
( )∫−
−=
∂
∂ 2/1
2/1
2]0[2
]0[
dFFHs
s
MSE
d ( ) ( )∫−
−=
∂
∂ 2/1
2/1
2cos2][
][
dFFHFnns
ns
MSE
dπ
0
][
=
∂
∂
ns
MSE
( )∫−
=
2/1
2/1
]0[ dFFHs d ( ) ( )∫−
=
2/1
2/1
2cos2][ dFFHFnns dπ
[ ] [0]
[ ] [ ]/ 2 for n=1,2,...,k
[ ] [ ]/ 2 for n=1,2,...,k
[ ] 0 for n<0 and n N
h k s
h k n s n
h k n s n
h n
=
+ =
− =
= ≥](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-51-2048.jpg)


![Feb.2008 DISP Lab 54
References
[1]B. Jackson, Digital Filters and Signal
Processing, Kluwer Academic Publishers 1986
[2]Dr. DePiero, Filter Design by Frequency
Sampling, CalPoly State University
[3]W.James MacLean, FIR Filter Design
Using Frequency Sampling
[4] 蒙以正 , 數位信號處理 , 旗標 2005
[5]Maurice G.Bellanger, Adaptive Digital
Filters second edition, Marcel dekker 2001](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-54-2048.jpg)
![Feb.2008 DISP Lab 55
References
[6] Lawrence R. Rabiner, Linear Program
Design of Finite Impulse Response Digital
Filters, IEEE 1972
[7] Terrence J mc Creary, On Frequency
Sampling Digital Filters, IEEE 1972](https://image.slidesharecdn.com/firandiirfilterdesign-140429072759-phpapp02/75/Fir-and-iir-filter_design-55-2048.jpg)