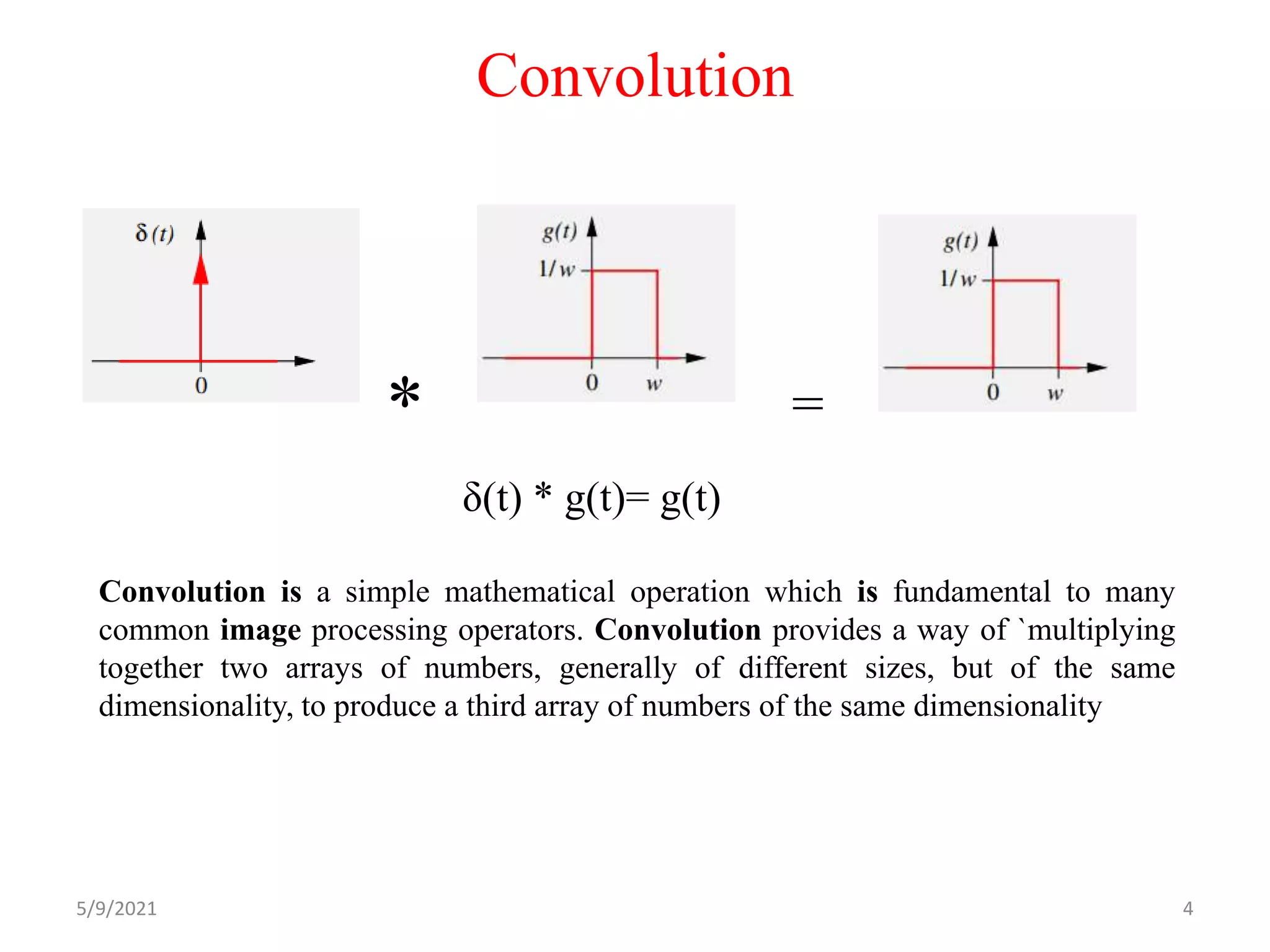
The document discusses convolution, which is a mathematical operation used in signal and image processing. Convolution provides a way to multiply two arrays of numbers to produce a third array. It defines convolution as an integral that calculates the output of a linear time-invariant system by integrating the product of the input and impulse response functions. The key properties of convolution are that it is commutative, distributive, and associative. Examples are provided to demonstrate calculating the convolution of different signals.

1. CONVOLUTION
Dr. Vandana Malode
Department of ECT
MGMU JNEC
5/9/2021 1
source:open source free internet

2. Content
• Definition of impulse response (LTI System)
• Basic concept of convolution
• Prove Convolution Integral
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡 − τ)dτ
• Properties of convolution
• Example of convolution integral.
5/9/2021 2

3. Definition of Impulse Response
• Impulse response is the response of a relaxed LTI
system to unit impulse δ(t)
• LTI system is said to be initially relaxed system if Zero input produced zero
output. In case of certain system; if we apply zero input then output is not
zero. Some value of output is obtained. Such system are called as non
relaxed system
5/9/2021 3
Relaxed LTI
System
Input x(t)=δ(t) output y(t)=h(t)

4. Convolution
* =
δ(t) * g(t)= g(t)
5/9/2021 4
Convolution is a simple mathematical operation which is fundamental to many
common image processing operators. Convolution provides a way of `multiplying
together two arrays of numbers, generally of different sizes, but of the same
dimensionality, to produce a third array of numbers of the same dimensionality

5. Find Convolution Integral
• Superposition integral
x(t) = −∞
∞
𝑥(τ)δ(𝑡 − τ)dτ
• Convolution integral
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡 − τ)dτ
5/9/2021 5

6. LTI(Linear time invariant or LSI) system
• Consider an LTI system which is initially relaxed at
t=0. If the input to the system is an impulse, then the
output of the system is denoted by h(t) and is called
the impulse response of the system
• Remark: A CT LTI system is completely described by
its impulse response h(t)
5/9/2021 6

7. • Consider the CT SISO system:
• If the input signal is and the
system has no energy at , the output
is called the impulse response of
the system
CT Unit-Impulse Response
( )
h t
( )
t

( ) ( )
x t t


( ) ( )
y t h t

( )
y t
( )
x t System
LTI
System
0
t 

5/9/2021 7

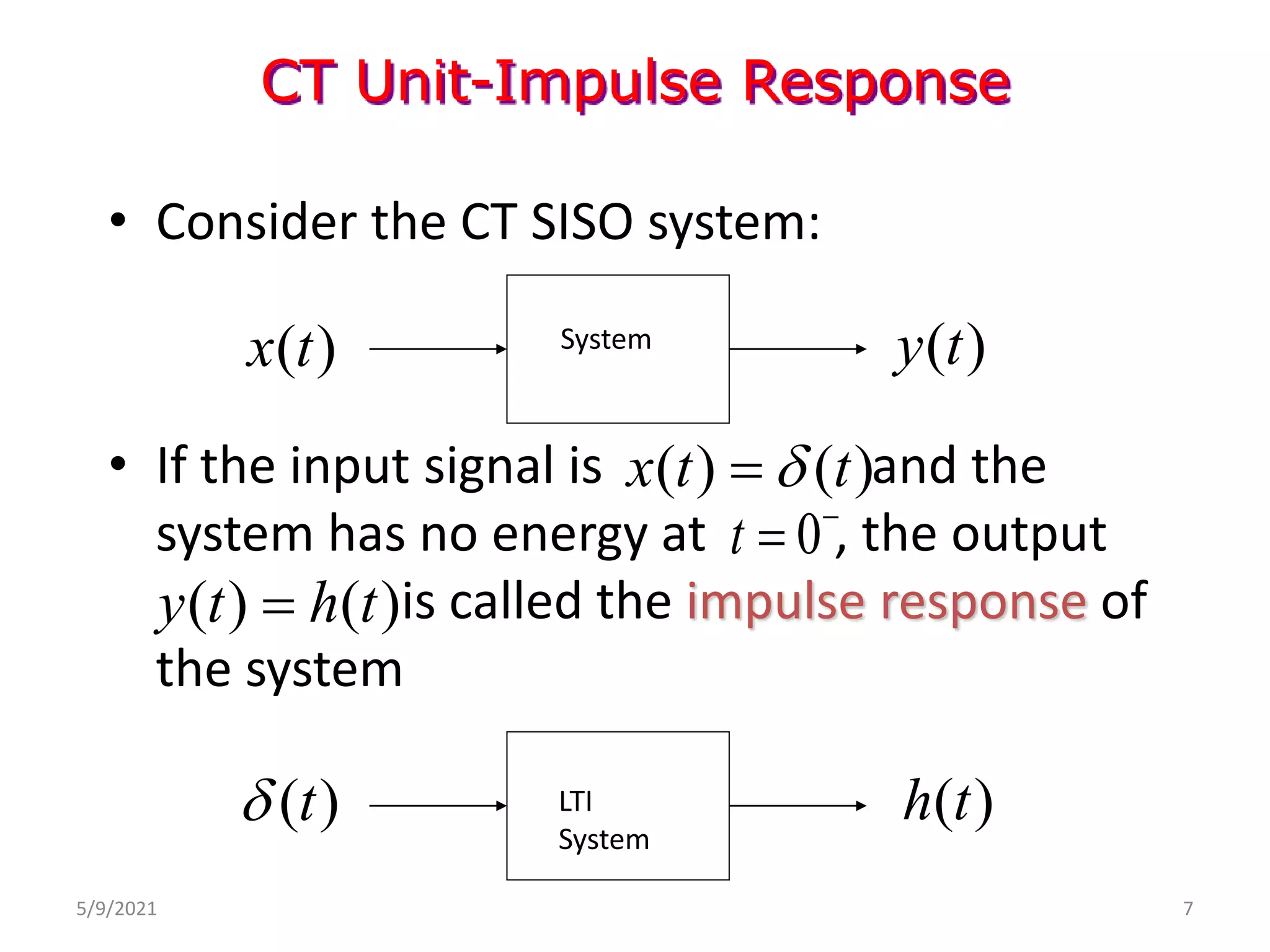
8. • The impulse response is denoted as:
h(t)=T[δ(t)]
We know that any arbitrary signal x(t) can be represented as:
The system output is given by : y(t)=T[x(t)]
• y(t)= T[ ]
 For linear system
• y(t) = −∞
∞
𝑥(τ)𝑇[δ(𝑡 − τ)]dτ------(1)
5/9/2021 8

9. • If the response of the system due to impulse δ(t) is h(t), then the
response of the system due to delayed impulse is
h(t,τ)=T[δ(t-τ)]
put this value in equation 1
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡, τ)dτ----------(2)
 For a time invariant system, the output due to delayed by τ sec
is equal to the output delayed by τ sec. i.e.
h(t,τ)=h(t-τ)
Time invariant----shifting
Put this value in equation (2)
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡 − τ)dτ
This is called convolution integral or simply convolution.
The convolution of two signals x(t) and h(t) can be represented as
y(t)= x(t) * h(t)
5/9/2021 9

10. Response of linear system
• In General , the lower limit and upper limit of integration in the
convolution integral depend on whether the signal x(t) and the impulse
response h(t) are causal or not.
1] If a noncausal signal is applied to a noncausal system
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡 − τ)dτ if both x(t) and h(t) are noncausal
2] If a noncausal signal is applied to a causal system
y(t) = −∞
𝑡
𝑥(τ)ℎ(𝑡 − τ)dτ if x(t) is non causal and h(t)is causal
3]If a causal signal is applied to a noncausal system
y(t) = 0
∞
𝑥(τ)ℎ(𝑡 − τ)dτ if x(t) is causal and h(t)is non causal
4]If a causal signal is applied to a causal system
y(t) = 0
𝑡
𝑥(τ)ℎ(𝑡 − τ)dτ if both x(t) is causal and h(t) are causal
5/9/2021 10
signals and systems by A. Ananad Kumar

11. Properties of convolution Integral
• Let us consider two signals x1(t) and x2(t). The convolution of two
signals x1(t) and x2(t) is given by
x1(t) * x2(t)= −∞
∞
𝑥1(τ)𝑥2(𝑡 − τ)dτ
= −∞
∞
𝑥2(τ)𝑥1(𝑡 − τ)dτ
The properties of convolution are as follows:
Commutative property:
x1(t) * x2(t)= x2(t) * x1(t)
Distributive property:
x1(t) * [x2(t)+x3(t)]= [x1(t) * x2(t)]+[x2(t) * x3(t)]
Associative property:
x1(t) * [x2(t)*x3(t)]= [x1(t) * x2(t)]*x3(t)
5/9/2021 11
signals and systems by A. Ananad Kumar

12. Continue: Properties of convolution Integral
• Shift Property:
x1(t) * x2(t)=z(t)
x1(t) * x2(t-T)=z(t-T)
x1(t-T) * x2(t)=z(t-T)
x1(t-T1) * x2(t-T2)=z(t-T1-T2)
5/9/2021 12
signals and systems by A. Ananad Kumar

13. Find the convolution of the following signals
1] x1(t)=e-2tu(t) ; x2(t)=e-4tu(t)
2] x1(t)=tu(t) ; x2(t)=tu(t)
5/9/2021 13

14. 1] x1(t)=e-2tu(t) ; x2(t)=e-4tu(t)
We know that
x1(t) * x2(t)= −∞
∞
𝑥1(τ)𝑥2(𝑡 − τ)dτ
Put t=τ
Put the value of x1(τ) and x2(t-τ) in above
equation
= −∞
∞
e−2τu(τ) e-4(t-τ)u(t-τ) dτ
5/9/2021 14

15. Continue
Unit step u(τ)=1 for τ>0
u(t-τ)=1 for t-τ≥0 or τ<0
Hence u(τ) u(t-τ)=1 for 0 < τ <t
For all other values of u(τ ) u(t-τ)=0
x1(t) * x2(t) = 0
𝑡
e−2τ e-4(t-τ) dτ
= 0
𝑡
e−2τ e-4t e4τ dτ
= e-4t
0
𝑡
e2τ dτ
= e-4t [ e2τ /2]
= e-4t /2 [ e2t -1] fort≥0
= [ e-2t - e-4t ] /2
5/9/2021 15

16. 3] x1(t)=cost u(t) ; x2(t)=u(t)
We know that
x1(t) * x2(t)= −∞
∞
𝑥1(τ)𝑥2(𝑡 − τ)dτ
Put t=τ
Put the value of x1(τ) and x2(t-τ) in above
equation
x1(t) * x2(t)= −∞
∞
𝑐𝑜𝑠τ , 𝑢 τ 𝑢(𝑡 − τ)dτ
5/9/2021 16

17. Continue
• Hence u(τ) u(t-τ)=1 for 0 < τ <t
=0 Otherwise
x1(t) * x2(t)= 0
𝑡
𝑐𝑜𝑠τdτ
= [ sinτ]0
t
= sint-sin0
= sint for t≥0
5/9/2021 17

18. Find convolution of signal as shown in figure. Plot y(t)
5/9/2021 18

19. Solution: Put t=τ and x(τ)and h(-τ)
• According to definition of convolution
y(t) = −∞
∞
𝑥(τ)ℎ(𝑡 − τ)dτ
Case1: When t<0
There is no overlapping. Therefore y(t)=0
5/9/2021 19

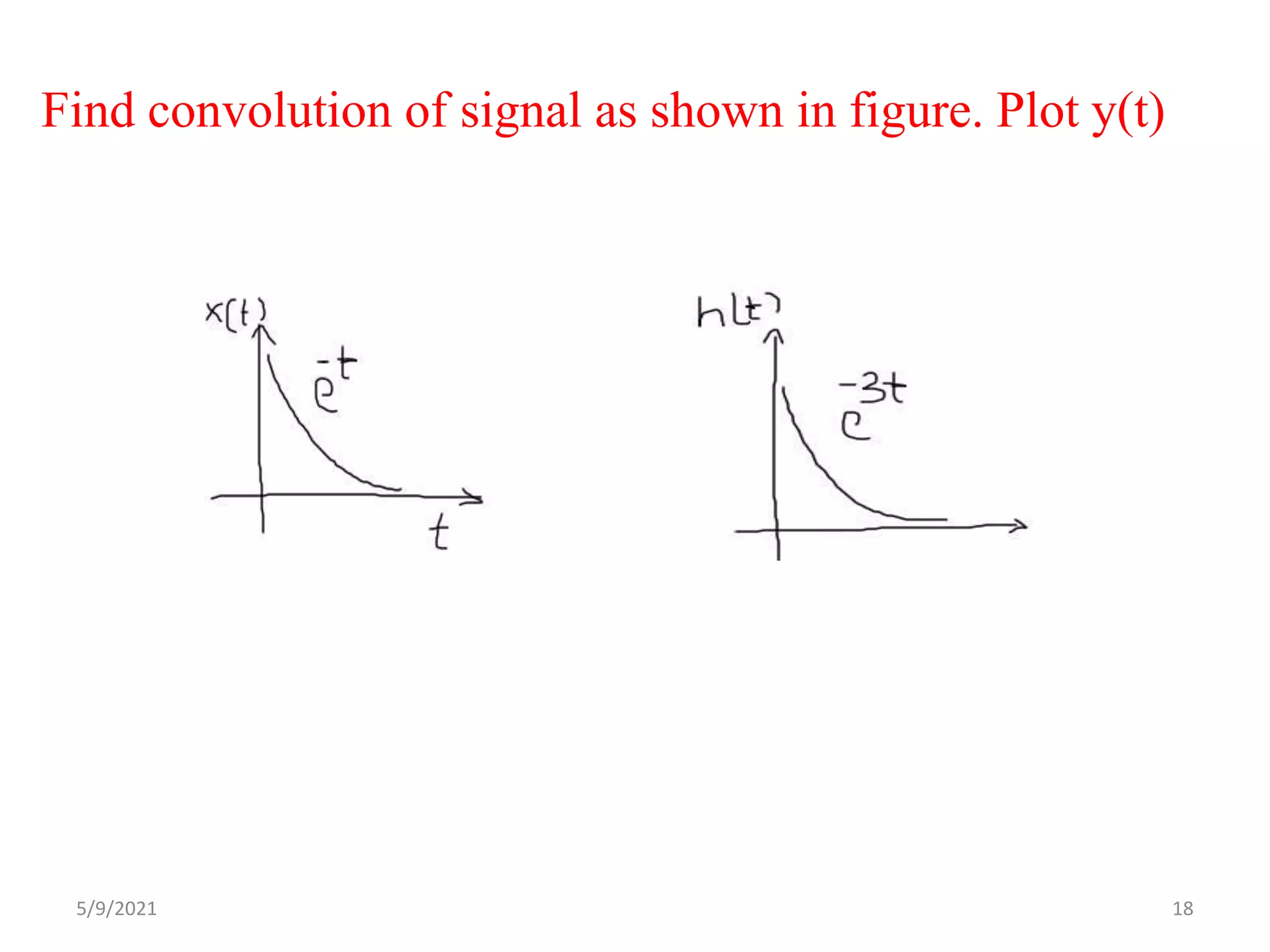
20. • Case2: When t>0
• This condition shown in figure
• Y(t)= 0
𝑡
e−τ e-3(-τ+t) dτ = e-3t/2 [ e-2t -1 ]
5/9/2021 20

21. 5/9/2021 21