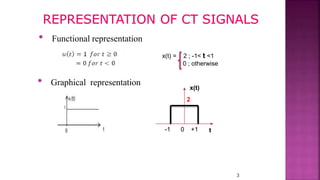
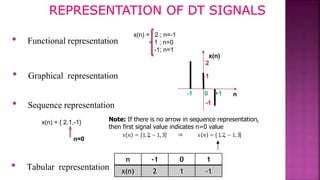
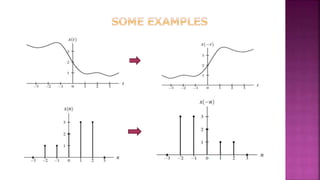
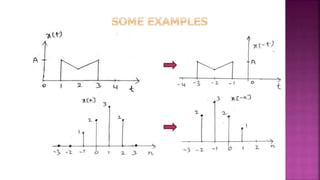
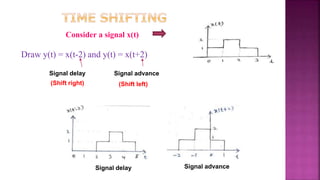
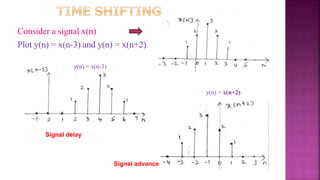
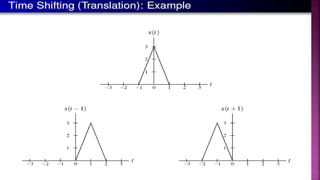
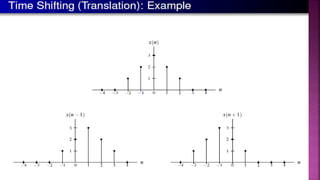
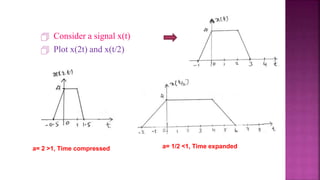
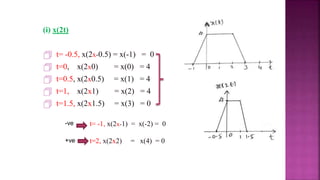
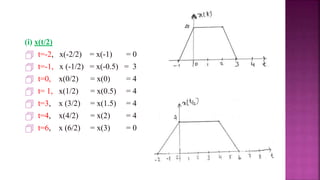
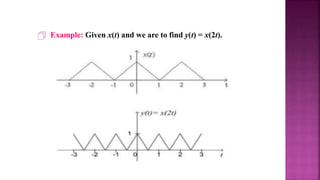
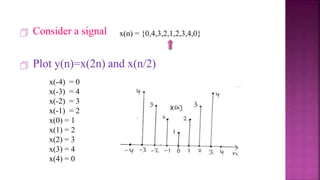
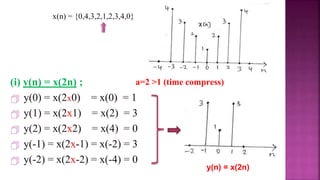
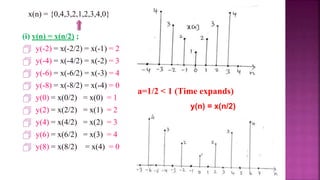
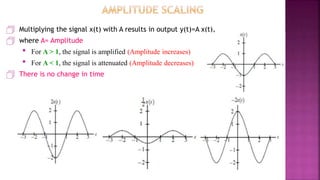
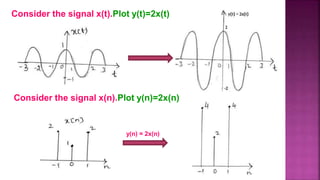
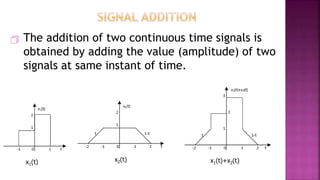
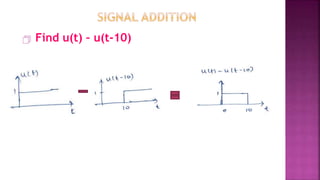
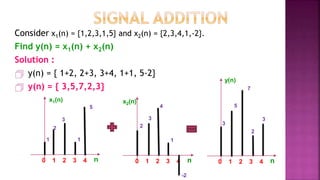
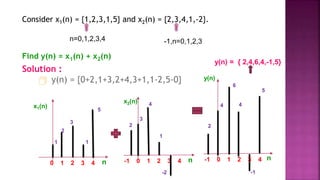
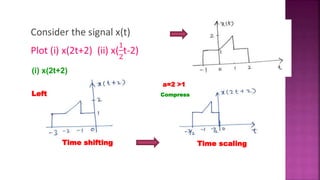
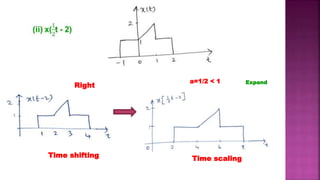
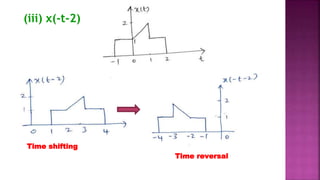
1. The document discusses various operations that can be performed on signals including time reversal, time shifting, time scaling, amplitude scaling, signal addition, and signal multiplication. 2. Examples are provided to demonstrate how to graphically represent signals and how the different operations change the signals. 3. Key steps are outlined for performing each operation including reversing the time axis, delaying or advancing signals, compressing or expanding the time axis, amplifying or attenuating signal amplitude, adding or multiplying signal values.

1. Dr.K.G.SHANTHI
Professor/ECE
shanthiece@rmkcet.ac.in
RMK College of Engineering and Technology
(Time Reversal, Time Shifting , Time Scaling, Amplitude scaling,
Signal addition, Signal Multiplication)

2. 2

3. 3
• Functional representation
x(t) = 2 ; -1< t <1
0 ; otherwise
-1 0 +1
x(t)
2
t
• Graphical representation

4. 4
• Functional representation
x(n) = 2 ; n=-1
1 ; n=0
-1; n=1
n
x(n)
2
1
-1
-1 0 +1
n -1 0 1
x(n) 2 1 -1
x(n) = { 2,1,-1}
n=0
Note: If there is no arrow in sequence representation,
then first signal value indicates n=0 value
• Graphical representation
• Sequence representation
• Tabular representation

5. 1. x(n) = 2n ; n ≥ 0
0 ; n < 0
2.x(n) = { 1,-2,3,2,-1,0,3}
Write the tabular representation of x(n)
5
Draw the graphical representation of x(n)

6. 6

7. Operation on Independent variable
Time Inversion or Time Folding or Time Reversal
Time Shifting
Time Scaling
Operation on Dependent variable
Amplitude scaling
Signal addition
Signal Multiplication
7
Signals

8.  In Time reversal, signal x(t) is reversed with respect to time
i.e. y(t) = x(-t) is obtained for the given function
 Time Folding: By folding the signal x(t) about t=0 (Rotating signal
by 1800 clockwise direction will give mirror image of signal
8
i.e x(-t)

9. 9

10. 10

11. 11

12.  The original signal x(t ) is shifted by an amount tₒ.
 Signal Delayed
 Signal Advanced
12
X(t) X(t- t0) Shift right
X(t) X(t + t0) Shift left

13. 13
Draw y(t) = x(t-2) and y(t) = x(t+2)
Signal delay
(Shift right)
Signal advance
(Shift left)
Signal delay Signal advance
Consider a signal x(t)

14. 14
Consider a signal x(n)
Plot y(n) = x(n-3) and y(n) = x(n+2)
Signal delay
Signal advance
y(n) = x(n-3)
y(n) = x(n+2)

15. 15

16. 16

17. 17

18.  Consider a signal x(t)
 Plot x(2t) and x(t/2)
18
a= 2 >1, Time compressed a= 1/2 <1, Time expanded

19. (i) x(2t)
 t= -0.5, x(2x-0.5) = x(-1) = 0
 t=0, x(2x0) = x(0) = 4
 t=0.5, x(2x0.5) = x(1) = 4
 t=1, x(2x1) = x(2) = 4
 t=1.5, x(2x1.5) = x(3) = 0
19
t= -1, x(2x-1) = x(-2) = 0
t=2, x(2x2) = x(4) = 0
-ve
+ve

20. (i) x(t/2)
 t=-2, x(-2/2) = x(-1) = 0
 t=-1, x (-1/2) = x(-0.5) = 3
 t=0, x(0/2) = x(0) = 4
 t= 1, x(1/2) = x(0.5) = 4
 t=3, x (3/2) = x(1.5) = 4
 t=4, x(4/2) = x(2) = 4
 t=6, x (6/2) = x(3) = 0
20

21.  Example: Given x(t) and we are to find y(t) = x(2t).
21

22.  Consider a signal
 Plot y(n)=x(2n) and x(n/2)
22
x(-4) = 0
x(-3) = 4
x(-2) = 3
x(-1) = 2
x(0) = 1
x(1) = 2
x(2) = 3
x(3) = 4
x(4) = 0
x(n) = {0,4,3,2,1,2,3,4,0}

23. (i) y(n) = x(2n) ;
 y(0) = x(2x0) = x(0) = 1
 y(1) = x(2x1) = x(2) = 3
 y(2) = x(2x2) = x(4) = 0
 y(-1) = x(2x-1) = x(-2) = 3
 y(-2) = x(2x-2) = x(-4) = 0
23
y(n) = x(2n)
a=2 >1 (time compress)
x(n) = {0,4,3,2,1,2,3,4,0}

24. (i) y(n) = x(n/2) ;
 y(-2) = x(-2/2) = x(-1) = 2
 y(-4) = x(-4/2) = x(-2) = 3
 y(-6) = x(-6/2) = x(-3) = 4
 y(-8) = x(-8/2) = x(-4) = 0
 y(0) = x(0/2) = x(0) = 1
 y(2) = x(2/2) = x(1) = 2
 y(4) = x(4/2) = x(2) = 3
 y(6) = x(6/2) = x(3) = 4
 y(8) = x(8/2) = x(4) = 0
24
y(n) = x(n/2)
a=1/2 < 1 (Time expands)
x(n) = {0,4,3,2,1,2,3,4,0}

25.  Multiplying the signal x(t) with A results in output y(t)=A x(t),
 where A= Amplitude
• For A ˃ 1, the signal is amplified (Amplitude increases)
• For A < 1, the signal is attenuated (Amplitude decreases)
 There is no change in time
25

26. 26
y(n) = 2x(n)
Consider the signal x(n).Plot y(n)=2x(n)
Consider the signal x(t).Plot y(t)=2x(t)

27.  The addition of two continuous time signals is
obtained by adding the value (amplitude) of two
signals at same instant of time.
27
x1(t) x2(t) x1(t)+x2(t)

28.  Find u(t) – u(t-10)
28

29. Consider x1(n) = {1,2,3,1,5} and x2(n) = {2,3,4,1,-2}.
Find y(n) = x1(n) + x2(n)
Solution :
 y(n) = { 1+2, 2+3, 3+4, 1+1, 5-2}
 y(n) = { 3,5,7,2,3}
29
0 1 2 3 4
x1(n)
1
2
3
5
n
1
0 1 2 3 4
x2(n)
2
3
4
n
1
-2
0 1 2 3 4
y(n)
3
2
3
5
n
7

30. Consider x1(n) = {1,2,3,1,5} and x2(n) = {2,3,4,1,-2}.
Find y(n) = x1(n) + x2(n)
Solution :
 y(n) = {0+2,1+3,2+4,3+1,1-2,5-0}
30
-1,n=0,1,2,3
n=0,1,2,3,4
0 1 2 3 4
x1(n)
1
2
3
5
n
1
-1 0 1 2 3 4
x2(n)
2
3
4
n
1
-2
-1 0 1 2 3 4
y(n)
2
-1
5
4
n
6
4
y(n) = { 2,4,6,4,-1,5}

31. Multiplication of two signals is obtained by multiplying the
value (amplitude) of two signals at same instant of time.
Consider
x1(n) = {1,2,3,4} and x2(n) = {2,1,3,2}
Find y(n) = x1(n) x2(n)
 y(n) ={ 1x2, 2x1, 3x3, 4x2}
 y(n) = { 2,2,9,8}
31
0 1 2 3
y(n)
2 2
9
8
n

32.  Multiply the signal values at all time or
specific time
32

33.  Follow the precedence rule, if Time shifting and
Time scaling , time reversal and amplitude
scaling occurs in same signal.
 Rule:
33
Amplitude
scaling
Time shifting Time reversal Time scaling

34. 34
(i) x(2t+2)
Time shifting Time scaling
Left
a=2 >1
Compress

35. 35
Time shifting Time scaling
Right
a=1/2 < 1 Expand

36. (iii) x(-t-2)
36
Time shifting
Time reversal

37. 37