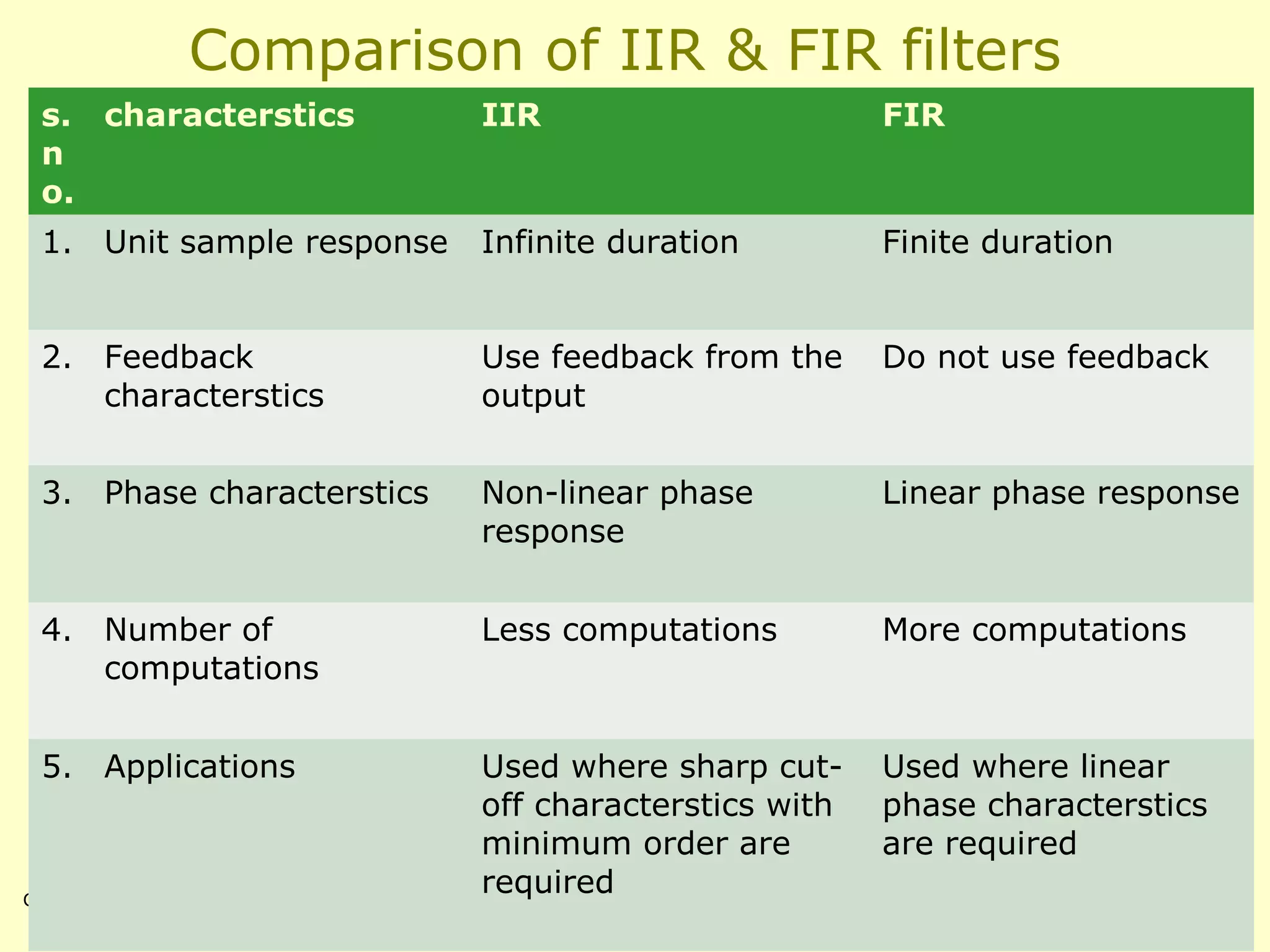
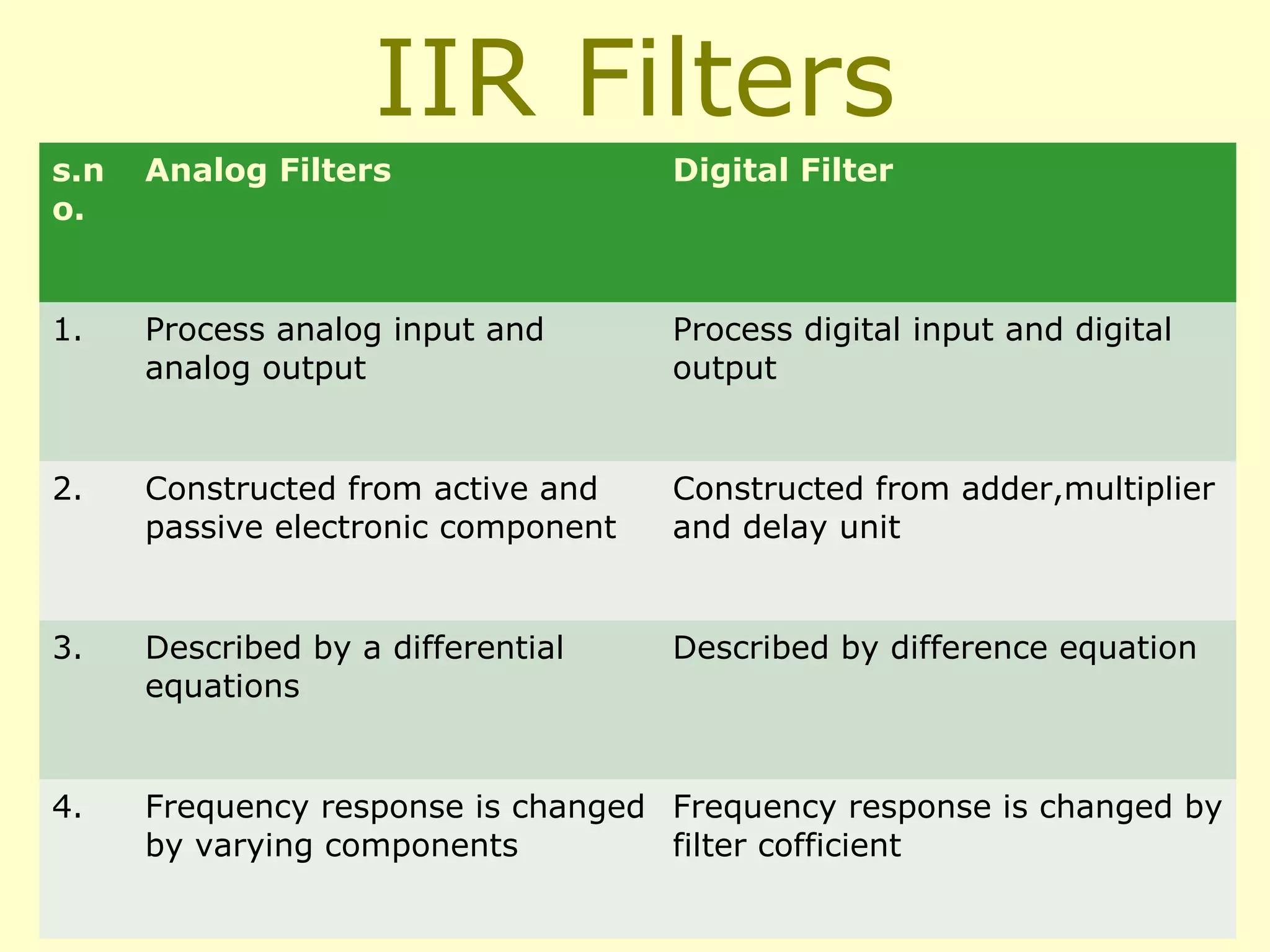
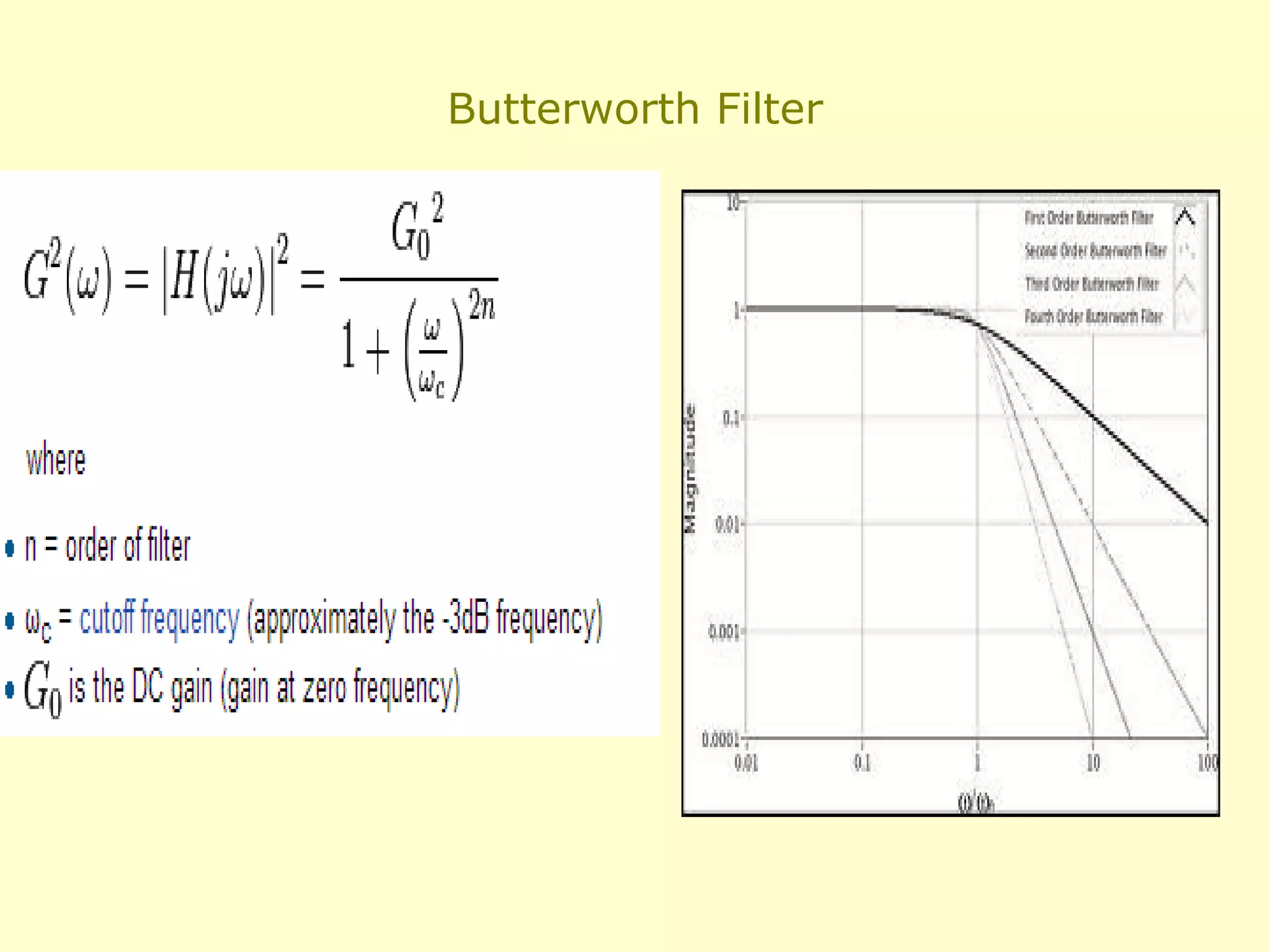
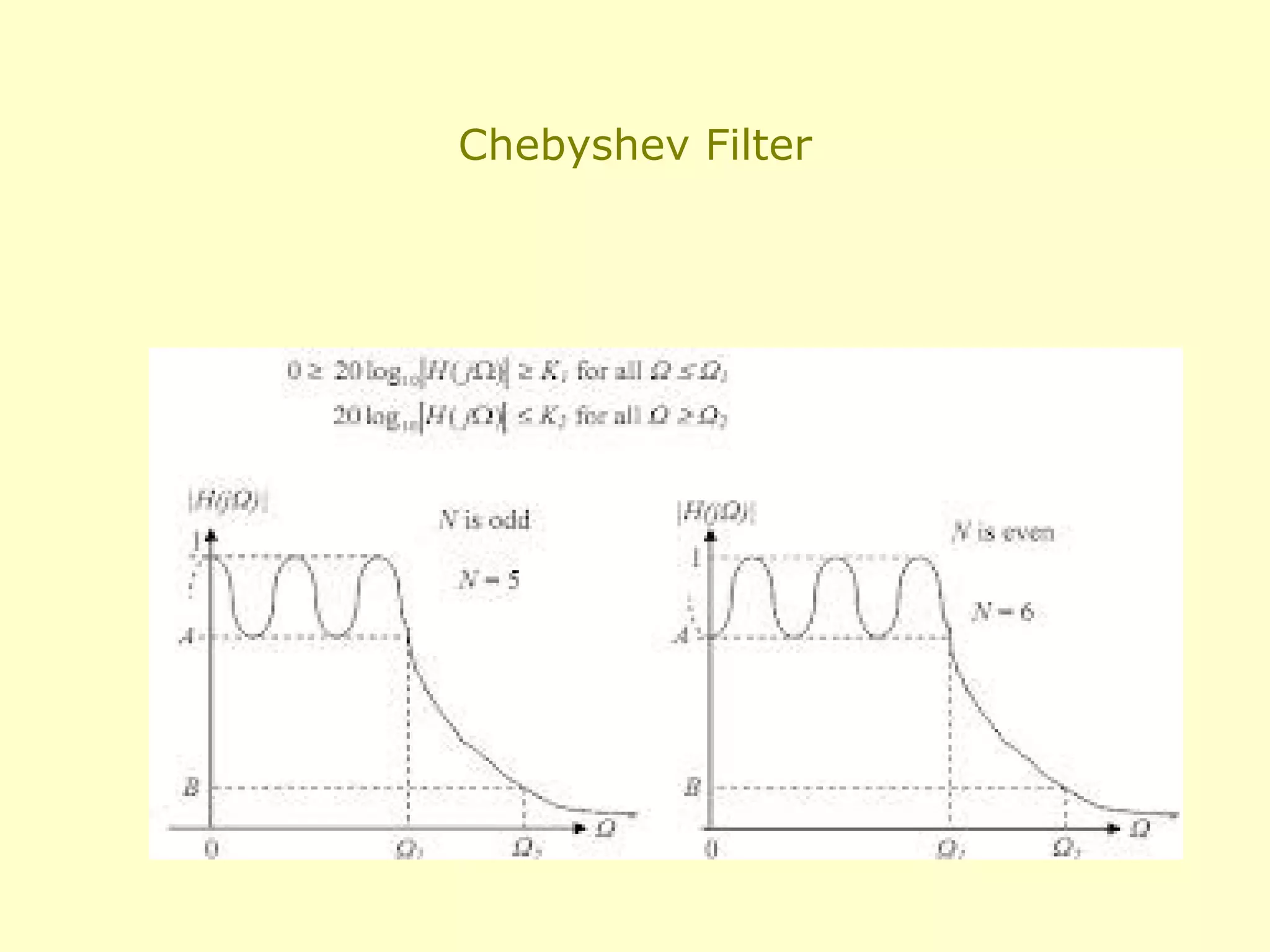
This document discusses the design of IIR and FIR filters. IIR (Infinite Impulse Response) filters are analog filters that use feedback and have non-linear phase responses. Common IIR design methods are impulse invariant, bilinear transformation, and approximation of derivatives. FIR (Finite Impulse Response) filters are digital filters with no feedback and linear phase responses. FIR filters are designed using windowing methods like rectangular, Hamming, and Kaiser windows which concentrate the filter response around the desired frequencies. IIR filters require less computation but FIR filters are required where linear phase response is needed such as data transmission and speech processing.

1. IIR Filter Design
&
FIR Filter Design
Utkarsh Kulshrestha
Kuldeep Saini

2. IIR Filter
Filters are used to remove the noise from the
baseband signals.
Filters gives the flat and smooth frequency
responses.
IIR filters are the Infinite impulse response filters.
Filters are of basically two types:1.Analog filter
2. Digital filters

3. IIR Filters
s.n
o.
Analog Filters
Digital Filter
1.
Process analog input and
analog output
Process digital input and digital
output
2.
Constructed from active and
passive electronic component
Constructed from adder,multiplier
and delay unit
3.
Described by a differential
equations
Described by difference equation
4.
Frequency response is changed Frequency response is changed by
by varying components
filter cofficient

4. IIR Filter
IIR design methods are as follows:1.Impulse Invariant method
2.Billinear method
3.Approximation of Derivatives

5. Impulse invariant method

6. IIR Filters
Bilinear Transformation:-
1- Bilinear transformation is transformation
from analog s-plane to digital z-plane.
2-It avoid the alising problem occurs in
impulse invariant method.
3-This conversion maps analog poles to
digital poles and analog zeros to digital
zeros.

7. IIR Filter
• Prewrapping Procedure:• Amplitude response of digital filter is expanded at the lower
frequencies and compressed at the higher frequencies in
comparision to the analog filter.
• Steps to design digital digital filter using bilinear
transformation technique :• 1-find prewrapping analog frequency
W=2/T tan(w/2)
• 2-using analog frequencies find H(s)
• 3-select the sampling rate of digital filter
substitute S=2/T(1-inv z/1+inv z)
Into transfer function H(s)

8. Butterworth Filter
The butterworth filter has magnitude
frequency response is flat in passband and
stopband.
As the filter order increases then the
butterworth response approximates the ideal
filter response.

9. Chebyshev filter
Type-1 Chebyshev filter
they have equiripple behavior In passband
and monotonic characterstics in stop band.
Type-2 Chebyshev filter
the magnitude response has maximally in
passband and equiripple in stop band.

10. Chebyshev filter
• Type-1

11. Butterworth Filter

12. Chebyshev Filter

13. FIR filter
It is a Digital filter which has Finite Impulse
response duration.
They have usually no feedback.
It has finite number of non zero terms.
FIR filters are used where linear phase response
in passband is required.
It is used for data transmission, speech
processing and always stable.

14. Design technique for FIR filter
1. Fourier series method
2. Windowing method
Rectangular window
Raised cosine window
Hamming window
Hanning window
Blackmann window
Bartlett window
Kaiser window
3.Frequency sampling method

15. Filter Design by Windowing
• Simplest way of designing FIR filters
• Method is all discrete-time no continuous-time involved
• Start with ideal frequency response
∞
π
1
jω
− jω n
Hd e = ∑ hd [n]e
hd [n] =
Hd e jω e jωndω
2π −∫π
n = −∞
( )
( )
• Choose ideal frequency response as desired response
• Most ideal impulse responses are of infinite length
• The easiest way to obtain a causal FIR filter from ideal is
hd [n] 0 ≤ n ≤ M
h[n] = 
else
 0
• More generally
h[n] = hd [n]w[n]
where
1 0 ≤ n ≤ M
w[n] = 
else
0

16. Properties of Windows
• Prefer windows that concentrate around DC in frequency
– Less distortion, closer approximation
• Prefer window that has minimal span in time
– Less coefficient in designed filter, computationally efficient
• So we want concentration in time and in frequency
– Contradictory requirements
• Example: Rectangular window
( ) = ∑e
We
jω
M
n=0
− jω n
1 − e − jω ( M + 1 )
sin[ ω(M + 1) / 2]
=
= e − jωM / 2
sin[ ω / 2]
1 − e − jω
351M Digital Signal Processing

17. Rectangular Window
• Narrowest main lob
– 4π/(M+1)
– Sharpest transitions at
discontinuities in
frequency
• Large side lobs
– -13 dB
– Large oscillation
around discontinuities
• Simplest window
possible
0≤n≤M
else
0
[n] = 1
w


18. Bartlett (Triangular) Window
• Medium main lob
– 8π/M
• Side lobs
– -25 dB
• Hamming window
performs better
• Simple equation
0 ≤ n ≤ M/2
 2n / M

w[n] = 2 − 2n / M M / 2 ≤ n ≤ M

0
else

18

19. Hanning Window
• Medium main lob
– 8π/M
• Side lobs
– -31 dB
• Hamming window
performs better
• Same complexity as
Hamming
1 
 2πn 
 1 − cos
 0 ≤ n ≤ M
w[n] = 2 
 M 

0
else


20. Hamming Window
• Medium main lob
– 8π/M
• Good side lobs
– -41 dB
• Simpler than Blackman

 2πn 
0.54 − 0.46 cos
 0≤n≤M
w[n] = 
 M 

0
else


21. Kaiser Window Filter Design Method
• Parameterized equation
forming a set of windows
– Parameter to change mainlob width and side-lob area
trade-off
w[ n] = {I ( Beta) | I (alpha ), | n |<= M − 1 2
0, otherwise
– I0(.) represents zeroth-order
modified Bessel function of 1st
kind
21

22. Determining Kaiser Window Parameters
• Given filter specifications Kaiser developed empirical equations
– Given the peak approximation error δ or in dB as A=-20log10 δ
– and transition band width ∆F = Fs − Fp
• The shape parameter alpha should be
0.1102( A − 8.7 )
A > 50


0.4
alpha = 0.5842( A − 21) + 0.07886( A − 21) 21 ≤ A ≤ 50

0
A < 21

• The filter order M is determined approximately by
FD
M=
+1
∆F

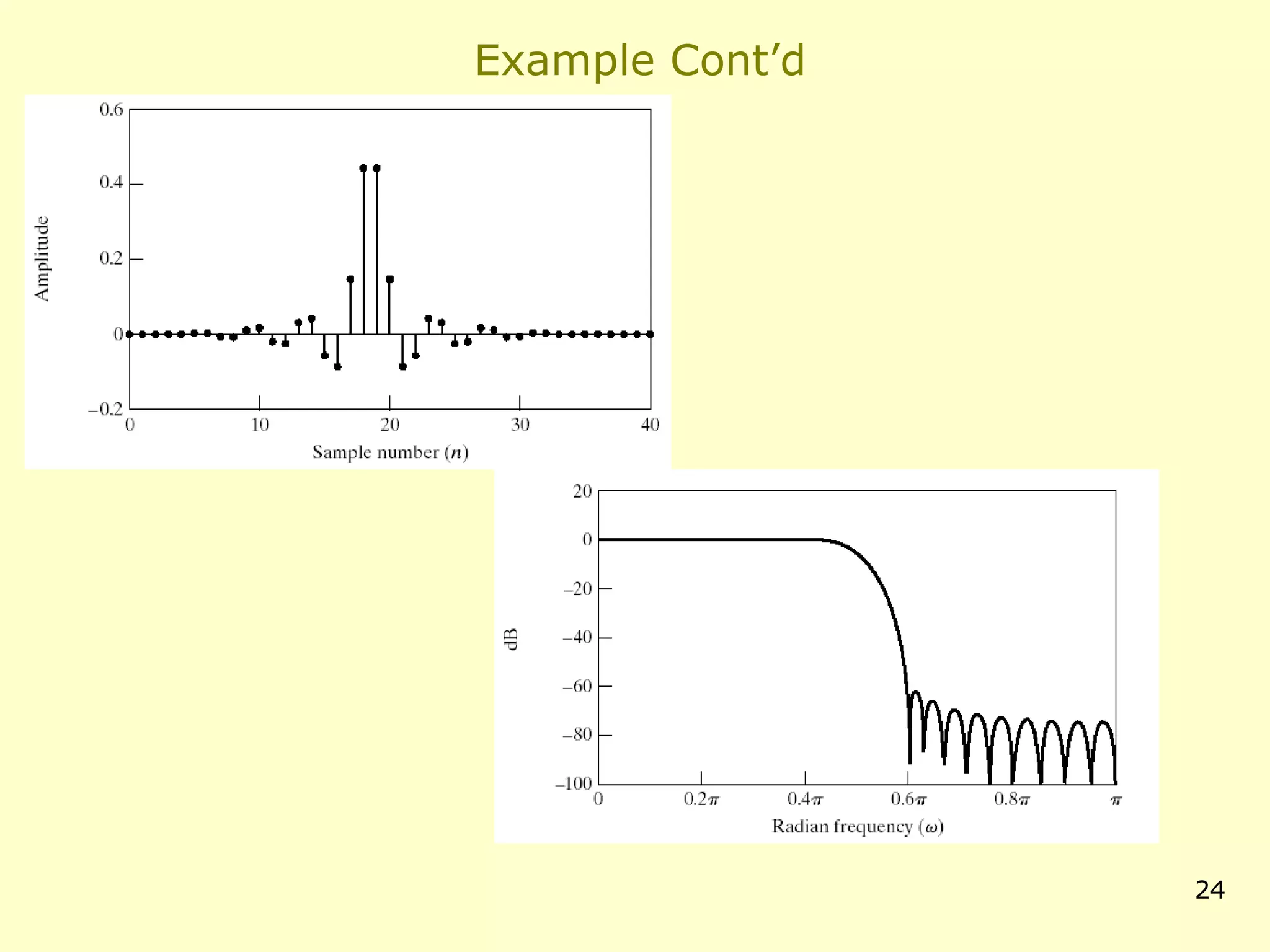
23. Example: Kaiser Window Design of a Lowpass Filter
• Specifications ωp = 0.4π, ωp = 0.6π, δ1 = 0.01, δ2 = 0.001
• Window design methods assume δ1 = δ2 = 0.001
• Determine cut-off frequency
– Due to the symmetry we can choose it to be ωc = 0.5π
• Compute
∆ω = ωs − ωp = 0.2π
A = −20 log10 δ = 60
• And Kaiser window parameters
alpha = 5.653
M = 37
• Then the impulse response is given as
2


 n − 18.5  

I0 5.653 1 − 


18.5  

h[n] =  sin[0.5π(n − 18.5) ] 



π(n − 18.5)
I0 (5.653)

0

0≤n≤M
else

24. Example Cont’d
24

25. Comparison of IIR & FIR filters
s. characterstics
n
o.
IIR
FIR
1. Unit sample response
Infinite duration
Finite duration
2. Feedback
characterstics
Use feedback from the
output
Do not use feedback
3. Phase characterstics
Non-linear phase
response
Linear phase response
4. Number of
computations
Less computations
More computations
5. Applications
Used where sharp cutoff characterstics with
minimum order are
required
Used where linear
phase characterstics
are required
Copyright (C) 2005 Güner Arslan
351M Digital Signal Processing
25

26. More on FIR &
IIR Next time…