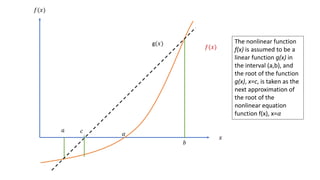
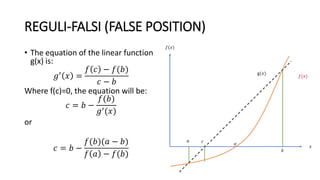
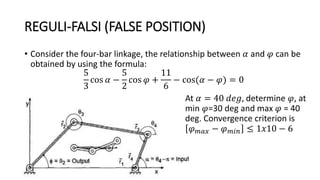
The Reguli-Falsi (False Position) method is a root-finding algorithm that uses linear interpolation to successively improve an approximation for the root of a function. It works by bracketing the root between two values, a and b, where the function values have opposite signs. The method assumes the function is linear within the interval and finds the root c of the linear interpolation function. If c is not the true root of the original function, it establishes a new bracket with one endpoint as the false position c. The process repeats, narrowing the range containing the root until the bracket width is within a specified tolerance.

1. NUMERICAL METHODS
TOPIC 2: REGULI-FALSI
(FALSE POSITION) METHOD

2. REGULI-FALSI (FALSE POSITION)
• The REGULI-FALSI method (also known as False Position linear-
interpolation method) involves obtaining values for two roots to the
equation f(x)=0 by trial-and-error.
• In this method, the nonlinear function f(x) is assumed to be a linear
function g(x) in the interval (a,b), and the root of the function g(x),
x=c, is taken as the next approximation of the root of the nonlinear
equation function f(x), x=𝛼
• The method is called linear interpolation method.

3. 𝑓(𝑥)
𝑥
𝑎
𝑏
g(𝑥)
𝑓(𝑥)
𝑐 𝛼
The nonlinear function
f(x) is assumed to be a
linear function g(x) in
the interval (a,b), and
the root of the function
g(x), x=c, is taken as the
next approximation of
the root of the
nonlinear equation
function f(x), x=𝛼

4. REGULI-FALSI (FALSE POSITION)
• The root of the linear equation
function g(x), that is x=c, is not the
root of the linear function f(x).
• It is a false position (in Latin, Regula
Falsi), which gives the method its
name.
• We now have two interval (a,c) and
(c,b).
• As in the bisection method, the
interval containing the root of the
nonlinear function f(x) is retained.

5. REGULI-FALSI (FALSE POSITION)
• The equation of the linear function
g(x) is:
𝑔′
𝑥 =
𝑓 𝑐 − 𝑓(𝑏)
𝑐 − 𝑏
Where f(c)=0, the equation will be:
𝑐 = 𝑏 −
𝑓(𝑏)
𝑔′(𝑥)
or
𝑐 = 𝑏 −
𝑓(𝑏)(𝑎 − 𝑏)
𝑓 𝑎 − 𝑓(𝑏)

6. REGULI-FALSI (FALSE POSITION)
• Consider the four-bar linkage, the relationship between 𝛼 and 𝜑 can be
obtained by using the formula:
5
3
cos 𝛼 −
5
2
cos 𝜑 +
11
6
− cos(𝛼 − 𝜑) = 0
At 𝛼 = 40 𝑑𝑒𝑔, determine 𝜑, at
min 𝜑=30 deg and max 𝜑 = 40
deg. Convergence criterion is
𝜑𝑚𝑎𝑥 − 𝜑𝑚𝑖𝑛 ≤ 1𝑥10 − 6

7. REGULI-FALSI (FALSE POSITION)
• Look for recent study/innovation on the application of Reguli-Falsi in
your specific field.
• Summary shall be submitted in 1 page
• No duplication