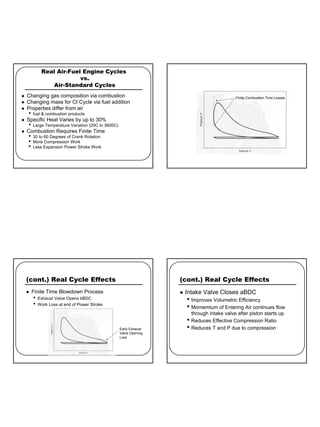
This document discusses the assumptions and equations used in air-standard cycle analysis of internal combustion engines. It covers: - The assumptions of the ideal air-standard cycle, including constant specific heats, reversible processes, and no combustion. - The relevant thermodynamic equations for analyzing the Otto cycle of intake, compression, combustion, expansion, exhaust. - How real engine cycles differ from the ideal cycle assumptions due to varying composition and properties during combustion, finite combustion duration, valve overlap effects. 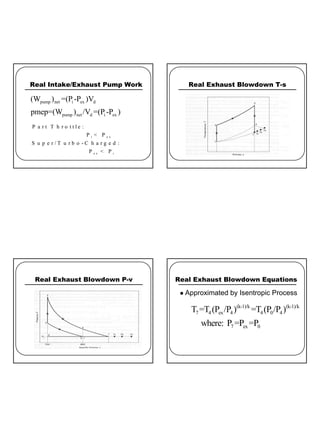- How to account for pump work from intake/exhaust pressures and residual exhaust gases in the clearance volume.

1. 1
I.C. Engines
ME 4803
Engine Cycle Analysis
Dr. Sam V. Shelton
Cycle Analysis
z Actual Cycles:
• Variable Composition (combustion) with Gas
Mixtures (CO2, H2O, N2)
z Air-Standard Cycle:
• Simplified and more manageable
• Determines Important Design Parameters
• Reasonable accuracy, particularly w.r.t.
sensitivity to design parameters
Air-Standard Assumptions
• Working Fluid is air
• Mass is constant (actually variation 7%)
• Closed Cycle
• Recirculated Air
• Heat Exchangers for heat rejection and
addition
• No Internal Combustion
(cont.) Air-Standard Assumptions
z Ideal Processes
• Constant pressure exhaust at 1 atms.
• Normally aspirated cycles have constant
pressure intake at 1 atms
• Turbo/Supercharged cycles have constant
pressure > 1 atms.
• Compression and Expansion are adiabatic
isentropic with contant specific heats

2. 2
(cont.) Air-Standard Assumptions
z Heat addition is at constant volume (SI)
or constant pressure (CI)
z Exhaust blowdown at constant volume
z All processes are reversible
Air-Standard Applicable Equations
z Ideal Gas Properties:
P
v
P v= R T
P V = m R T
P = ρ R T
d h = c d T
d u = c d T
(cont.) Air-Standard Applicable Equations
z Isentropic Compression and Expansion:
k
k-1
(1-k)/k
Pv =constant
Tv =constant
TP =constant
1-2 2 2 1 1
2 1
w =(P v -P v )/(1-k)
= R(T -T )/(1-k)
(cont.) Air-Standard Applicable Equations
• Work in Isentropic Expansion or Compression
• constant specific heats

3. 3
Air Standard Otto Cycle
z 1-2: Isentropic Compression
z 2-3: Constant Volume Heat Additioin
z 3-4: Isentropic Expansion
z 4-5: Constant Volume Heat Rejection
z 5-6: Exhaust at Ambient Pressure
z 6-1: Intake at 1 atms
• Higher than 1 atms if super/turbo-charged
Otto Cycle Thermodynamic Analysis
• Applying Applicable Thermodynamic Equations
6-1: Intake
1-2: Compression
2-3: Constant Volume Heat Addition
3-4: Power Stroke (Expansion)
4-5: Constant Volume Heat Rejection
5-6: Exhaust

4. 4
Intake Process 1-6:
1 6 0
P =P =P
6-1 0 1 6
w =P(v -v )
Isentropic Compression 1-2:
1 1 1
2 1 1 2 1 1 2 1
( / ) ( / ) ( )
k k k
c
T T v v T V V T r
− − −
= = =
2 1 1 2 1 1 2 1
( / ) ( / ) ( )
k k k
c
P P v v P V V P r
= = =
1 2 0
q − =
1-2 2 2 1 1 2 1
1 2 v 1 2
w =(P v -P v )/(1-k)=R(T -T )/(1-k)
=(u -u )=c (T -T )
Constant Volume Heat Input 2-3:
3 2 TDC
v =v =v
2-3
w =0
HV c v 3 2
Q η =(AF+1)c (T -T )
2-3 in v 3 2 3 2
q =q =c (T -T )=(u -u )
Isentropic Expansion 3-4:
3-4
q =0
k-1 k-1 k-1
4 3 3 4 3 3 4 3 c
T =T (v /v ) =T (V /V ) =T (1/r )
k k k
4 3 3 4 3 3 4 3 c
P =P (v /v ) =P (V /V ) =P (1/r )
3-4 3 4 v 3 4
w =(u -u )=c (T -T )

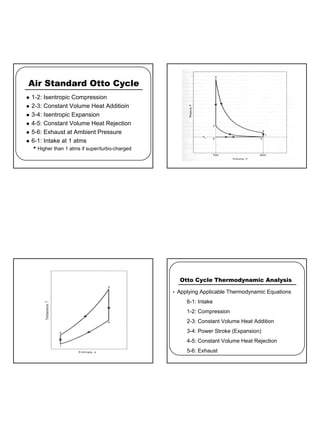
5. 5
Constant Volume Heat Rejection 4-5:
5 4 1 B D C
v = v = v = v
4 -5
w = 0
4 -5 o u t v 5 4 5 4 v 1 4
q = q = c (T -T )= (u -u )= c (T -T )
Blow Down
Exhaust Stroke 5-6:
5 6 0
P =P =P
5-6 0 6 5 0 6 1
w =P (v -v )=P (v -v )
Thermal Efficiency
z From Definition and Previous Process Eqns:
[ ]
t, net in out in
OTTO
v 4 1 v 3 2
η = w / q =1-( q / q )
=1- c (T -T )/c (T -T )
( )
k-1
t, 1 2
OTTO
η =1- 1/ v /v
 
 
k-1
t, c
OTTO
η =1-(1/r )
By using Isentropic Expansion and Compression Eqns:
(cont.) Thermal Efficiency
z Note: Thermal Efficiency and Work Output/cycle
t, c
OTTO
c BDC TDC
η =Function(r Only)
r compression ratio only =V /V
=
Higher Compression Ratio is Win/Win.
Higher Efficiency and Higher Power

6. 6
Real Air-Fuel Engine Cycles
vs.
Air-Standard Cycles
z Changing gas composition via combustion
z Changing mass for CI Cycle via fuel addition
z Properties differ from air
• fuel & combustion products
z Specific Heat Varies by up to 30%
• Large Temperature Variation (20C to 3600C)
z Combustion Requires Finite Time
• 30 to 60 Degrees of Crank Rotation
• More Compression Work
• Less Expansion Power Stroke Work
Finite Combustion Time Losses
(cont.) Real Cycle Effects
z Finite Time Blowdown Process
• Exhaust Valve Opens bBDC
• Work Loss at end of Power Stroke
Early Exhaust
Valve Opening
Loss
(cont.) Real Cycle Effects
z Intake Valve Closes aBDC
• Improves Volumetric Efficiency
• Momemtum of Entering Air continues flow
through intake valve after piston starts up
• Reduces Effective Compression Ratio
• Reduces T and P due to compression

7. 7
(cont.) Real Cycle Effects
z Finite Valve Opening and Closing Times
• Amplifies the previous effect of early Exhaust
Valve Opening and Late Intake Closing
• Causes Valve “Overlap” at TDC
• Both valves open simultaneously at TDC
Summary: Real Cycle Effects
z Errors of Real Cycle Effects vs. Air Standard
Effects not Large
z Some Errors tend to cancel, e.g., Specific Heats
z Real Cycle Efficiency Less than Air Standard
Calculated Values by about 15%
t,Actual t,Otto
η 0.85η
≈
Reall Part Throttle SI Cycle
Negative Pump Work
Real Turbo/Supercharged SI Cycle Effect
Positive Pump Work

8. 8
Real Intake/Exhaust Pump Work
pump net i ex d
pump net d i ex
(W ) =(P -P )V
pmep=(W ) /V =(P -P )
i e x
e x i
P a r t T h r o t t l e :
P < P
S u p e r / T u r b o - C h a r g e d :
P < P
Real Exhaust Blowdown T-s
Real Exhaust Blowdown P-v Real Exhaust Blowdown Equations
z Approximated by Isentropic Process
(k-1)/k (k-1)/k
7 4 ex 4 4 0 4
7 ex 0
T =T (P /P ) =T (P /P )
where: P =P =P

9. 9
Residual Exhaust in Intake Gases
z Residual Exhaust
Gases in Clearance
Volume, Vc, at TDC
Starting Intake
Stroke
r ex m
x =m /m
Calculating Residual Exhaust
z Using Energy Conservation to calculate T7:
ex ex a a m m
m h +m h =m h
m 1 r e x r a
e x 7
(T ) = x T + (1 -x )T
w h e re :
T T
=
(Cont.) Calculating Residual Exhaust
z Again, approximating blowdown as isentropic:
k
4 7 7 4 4 ex 4 0
P /P =(v /v ) =P /P =P /P
k
3 7 7 3 3 ex 3 0
P /P =(v /v ) =P /P =P /P
ex 5 ex 5 7 1 7
m =V /v =V /v =V /v
(cont.) Calculating Residual Exhaust
7 7 7 7 atm
v RT / P ; P P
= ≈
r 2 7 2 7
r
x =(V /v )=V /v
3% x 7%
< <
Exhaust Residual Examples: 3-2 & 3-3