Download as PDF, PPTX
Uploaded bySoumith V
Air standard cycles
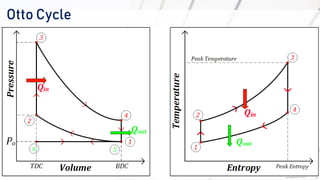
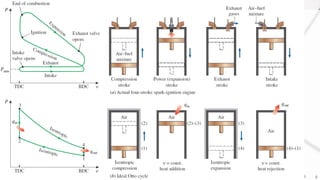
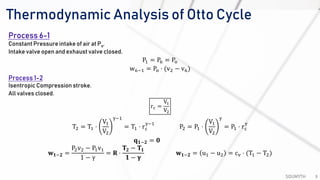
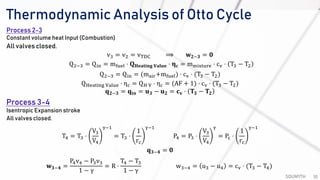
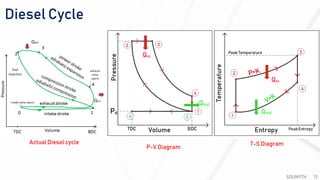
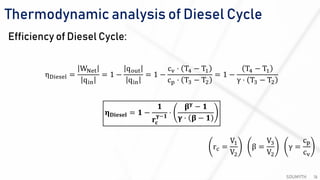
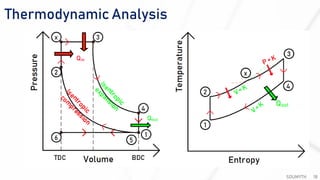
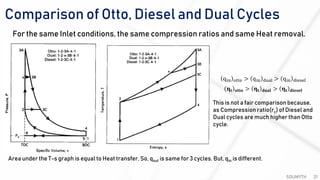
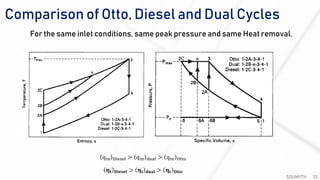
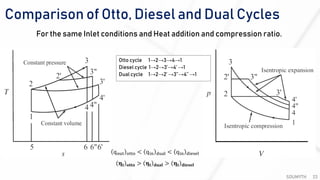
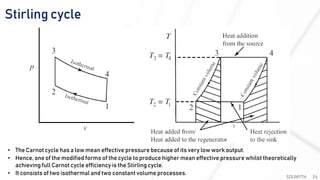
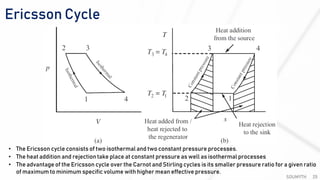
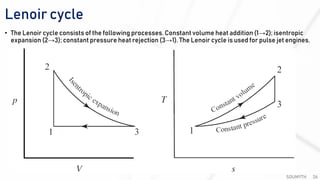
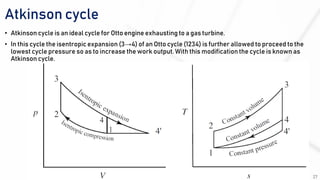
The document discusses various air standard cycles that are used to model internal combustion engine processes, including the Otto, Diesel, and dual cycles. It provides details on the assumptions and thermodynamic processes that define each cycle. The Otto cycle consists of four processes: constant-pressure intake, isentropic compression, constant-volume combustion, and isentropic expansion. The Diesel cycle models combustion as a constant-pressure process rather than constant volume. The dual cycle models combustion as both constant-volume and constant-pressure processes. Comparisons are made between the cycles in terms of their heat transfer and thermal efficiencies.
More Related Content
Similar to Air standard cycles
Air standard cycles
- 1.
- 2. Introduction SOUMYTH 2 In orderto understand internal combustion engine processes, it is advantageous to analyse the performance of an idealized closed cycle that closely approximates the real cycle i.e., Air standard cycle. It is based on following assumptions, • Working medium is assumed to be perfect gas and follows the relation PV = mRT. • There is no change in the mass of the working medium ( ሶ𝐦=0). • All the processes that constitute the cycle are reversible. • Heat is assumed to be supplied from a constant high temperature source and not from chemical reactions during the cycle. • Some heat is assumed to be rejected to a constant low temperature sink during the cycle. • It is assumed that there are no heat losses from the system to the surroundings. • The working medium has constant specific heats throughout cycle. • The physical constants viz., Cp, Cv, γ and M of the working medium are the same as those of air at standard atmospheric conditions.
- 3. Carnot Cycle SOUMYTH 3 •This cycle consists of two isothermal and reversible Adiabatic processes. • Carnot cycle is a perfect cycle and engines can be compared with it to judge the degree of perfection.
- 4. Carnot Cycle SOUMYTH 4 ηCarnot= Work done by the system during the cycle (𝐖) Heat supplied to the system during the cycle 𝐐 𝐬 W = Qs − Qr Qr = mRT1 ⋅ loge V1 V2 Qs = mRT3 ⋅ loge V4 V3 ηCarnot = mRT3 ⋅ loge V4 V3 − mRT1 ⋅ loge V1 V2 mRT3 ⋅ loge V4 V3 = T3 − T1 T3 V4 V1 = V3 V2 ηCarnot = 1 − T1 T3 • Increase in thermal efficiency can be achieved only by increasing the source temperature (T3). • Between two fixed temperatures Carnot cycle has the maximum possible efficiency compared to other air standard cycles.
- 5.
- 6.
- 7. Otto Cycle SOUMYTH 7 Theintake stroke of the Otto cycle starts with the piston at TDC and is a constant-pressure process at an inlet pressure of one atmosphere (6-1). For real engine, inlet pressure will be at a pressure slightly less than atmospheric due to pressure losses in the inlet air flow. The temperature of the air during the inlet stroke is increased as the air passes through the hot intake manifold. The second stroke of the cycle is an Isentropic compression from BDC to TDC (1-2). In a real engine, the beginning of the stroke is affected by the intake valve not being fully closed until slightly after BDC. The end of compression is affected by the firing of the spark plug before TDC. There is an increase in pressure during the compression stroke, but the temperature within the cylinder is increased substantially due to compressive heating. The third stroke of the cycle is a Constant-Volume heat input process 2-3 at TDC. In real engine, constant volume process is replaced by Combustion process which occurs at nearly Constant volume conditions. In a real engine combustion is started slightly before TDC, reaches its maximum speed near TDC, and is terminated a little after TDC. During combustion, a large amount of heat is added which results in peak temperature and peak pressure of air at the end of combustion.
- 8. Otto Cycle SOUMYTH 8 Inthe fourth stroke, high Pressure and Enthalpy produces power stroke which pushes the piston backwards (3-4). In a real engine, it is approximated as an Isentropic expansion, the beginning of the power stroke is affected by the last part of the combustion process. The end of the power stroke is affected by the exhaust valve being opened before BDC. During the power stroke, values of both the temperature and pressure within the cylinder decrease as volume increases from TDC to BDC. In the fifth stroke, near the end of power stroke, exhaust valve is opened and exhaust blowdown occurs. Pressure is reduced to exhaust manifold and large amount of enthalpy is carried away by exhaust gases. The exhaust valve is opened before BDC to allow for the finite time of blowdown to occur. In real cycle, exhaust blowdown is replaced with a Constant-Volume heat rejection, closed-system process 4-5. Pressure at the end has been reduced to atmospheric pressure. The last stroke of the four-stroke cycle now occurs as the piston travels from BDC to TDC. Process 5-6 is the exhaust stroke that occurs at a constant pressure of one atmosphere due to the open exhaust valve.
- 9. Thermodynamic Analysis ofOtto Cycle SOUMYTH 9 Process 6-1 Constant Pressure intake of air at Po. Intake valve open and exhaust valve closed. P1 = P6 = Po w6−1 = Po ⋅ (v2 − v6) Process 1-2 Isentropic Compression stroke. All valves closed. rc = V1 V2 T2 = T1 ⋅ V1 V2 γ−1 = T1 ⋅ rc γ−1 P2 = P1 ⋅ V1 V2 γ = P1 ⋅ rc γ 𝐪 𝟏−𝟐 = 𝟎 𝐰 𝟏−𝟐 = P2v2 − P1v1 1 − γ = 𝐑 ⋅ 𝐓𝟐 − 𝐓𝟏 𝟏 − 𝛄 𝐰 𝟏−𝟐 = u1 − u2 = cv ⋅ (T1 − T2)
- 10. Thermodynamic Analysis ofOtto Cycle SOUMYTH 10 Process 2-3 Constant volume heat Input (Combustion) All valves closed. v3 = v2 = vTDC ⟹ 𝐰 𝟐−𝟑 = 𝟎 Q2−3 = Qin = mfuel ⋅ 𝐐 𝐇𝐞𝐚𝐭𝐢𝐧𝐠 𝐕𝐚𝐥𝐮𝐞 ⋅ 𝛈 𝐜 = mmixture ⋅ cv ⋅ T3 − T2 Q2−3 = Qin = (mair+mfuel) ⋅ cv ⋅ (T3 − T2) QHeating Value ⋅ ηc = QH V ⋅ ηc = (AF + 1) ⋅ cv ⋅ (T3 − T2) 𝐪 𝟐−𝟑 = 𝐪𝐢𝐧 = 𝐮 𝟑 − 𝐮 𝟐 = 𝐜 𝐯 ⋅ 𝐓𝟑 − 𝐓𝟐 Process 3-4 Isentropic Expansion stroke All valves closed. T4 = T3 ⋅ V3 V4 γ−1 = T3 ⋅ 1 rc γ−1 P4 = P3 ⋅ V3 V4 γ = Pc ⋅ 1 rc γ−1 𝐪 𝟑−𝟒 = 𝟎 𝐰 𝟑−𝟒 = P4v4 − P3v3 1 − γ = R ⋅ T4 − T3 1 − γ w3−4 = u3 − u4 = cv ⋅ (T3 − T4)
- 11. Thermodynamic Analysis ofOtto Cycle SOUMYTH 11 Process 4-5 Constant volume Heat rejection. Exhaust valve open and intake valve closed. v5 = v4 = v1 = vBDC ⟹ 𝐰 𝟒−𝟓 = 𝟎 Q4−5 = Qout = mmixture ⋅ cv ⋅ T5 − T4 = mmix ⋅ cv ⋅ T1 − T4 q4−5 = 𝐪 𝐨𝐮𝐭 = 𝐜 𝐯 ⋅ 𝐓𝟓 − 𝐓𝟒 = u5 − u4 = cv ⋅ (T1 − T4) Process 5-6 Constant Pressure exhaust stroke at Po. Exhaust valve open and intake valve closed. P5 = P6 = Po w5−6 = Po ⋅ v6 − v5 = Po ⋅ (v6 − v1)
- 12. Diesel Cycle SOUMYTH 12 •Early CI engines injected fuel into the combustion chamber very late in the compression stroke. • Due to ignition delay and the finite time required to inject the fuel, combustion lasted into the expansion stroke. This kept the pressure at peak levels well past TDC. • This combustion process is best approximated as a constant-pressure heat input in an air-standard cycle. • In CI engines, the air is compressed to a temperature, that is above the auto ignition temperature of the fuel and combustion starts on the contact as the fuel is injected into the hot air.
- 13. Diesel Cycle SOUMYTH 13 ActualDiesel cycle P-V Diagram T-S Diagram
- 14. Thermodynamic analysis ofDiesel Cycle SOUMYTH 14 Process 6-1 Constant pressure Air intake W6−1 = Po ⋅ v1 − vo Process 1-2 Isentropic Compression stroke. T2 = T1 ⋅ V1 V2 γ−1 = T1 ⋅ rc γ−1 P2 = P1 ⋅ V1 V2 γ = P1 ⋅ rc γ q1−2 = 0 w1−2 = P2v2 − P1v1 1 − γ = u1 − u2 = cv ⋅ T1 − T2 Process 2-3 Constant pressure Heat Addition Q2−3 = Qin = mf ⋅ QHV ⋅ ηc = ma + mf ⋅ cp ⋅ T3 − T2 q2−3 = cp ⋅ T3 − T2 w2−3 = P2 ⋅ v3 − v2 = q2−3 − u3 − u2 → 𝐂𝐮𝐭𝐨𝐟𝐟 𝐫𝐚𝐭𝐢𝐨 𝛃 = V3 V2 Volume change ratio during combustion rc = V1 V2
- 15. Thermodynamic Analysis ofDiesel Cycle SOUMYTH 15 Process 3-4 Isentropic Expansion stroke T4 = T3 ⋅ V3 V4 γ−1 = T3 ⋅ 1 rc γ−1 P4 = P3 ⋅ V3 V4 γ = P3 ⋅ 1 rc γ−1 𝐪 𝟑−𝟒 = 𝟎 𝐰 𝟑−𝟒 = P4v4 − P3v3 1 − γ = R ⋅ T4 − T3 1 − γ w3−4 = u3 − u4 = cv ⋅ (T3 − T4) Process 4-5 Constant volume Heat rejection. v5 = v4 = v1 = vBDC 𝐰 𝟒−𝟓 = 𝟎 Q4−5 = Qout = mmixture ⋅ cv ⋅ T5 − T4 = mmix ⋅ cv ⋅ T1 − T4 q4−5 = 𝐪 𝐨𝐮𝐭 = 𝐜 𝐯 ⋅ 𝐓𝟓 − 𝐓𝟒 = u5 − u4 = cv ⋅ (T1 − T4) Process 5-6 Constant Pressure exhaust stroke at Po. P5 = P6 = Po w5−6 = Po ⋅ v6 − v5 = Po ⋅ (v6 − v1)
- 16. Thermodynamic analysis ofDiesel Cycle SOUMYTH 16 Efficiency of Diesel Cycle: ηDiesel = WNet qin = 1 − qout qin = 1 − cv ⋅ T4 − T1 cp ⋅ T3 − T2 = 1 − T4 − T1 γ ⋅ T3 − T2 𝛈 𝐃𝐢𝐞𝐬𝐞𝐥 = 𝟏 − 𝟏 𝐫𝐜 𝛄−𝟏 ⋅ 𝛃 𝛄 − 𝟏 𝛄 ⋅ 𝛃 − 𝟏 rc = V1 V2 β = V3 V2 γ = cp cv
- 17. Dual Cycle SOUMYTH 17 Indicatordiagram for Dual Cycle • The Dual cycle, also called a mixed cycle or limited pressure cycle, is a compromise between Otto and Diesel cycles. • C.I engines have higher compression ratios and S.I engines have higher efficiencies. • Instead of injecting fuel late in the compression stroke near TDC, modern C.I engines start to inject the fuel much earlier in the cycle somewhere around 200 bTDC. So, part of combustion occurs at constant volume and remaining at constant pressure. • Dual cycle is similar to Diesel cycle except for Heat input process.
- 18.
- 19. Thermodynamic Analysis SOUMYTH 19 Process2-x Constant volume Heat addition w2−x = 0 q2−x = cv ⋅ Tx − T2 = ux − u2 Pressure ratio α = Px P2 = P3 P2 = Tx T2 = 1 rc k ⋅ P3 P1 Process x-3 Constant pressure heat addition P3 = Px = Pmax qx−3 = cp ⋅ T3 − Tx = h3 − hx wx−3 = P3 ⋅ v3 − vx T3 = Tmax β = V3 Vx Qin = Q2−x + Qx−3 = mf ⋅ QHV ⋅ ηc qin = q2−x + q3−x = ux − u2 + h3 − hx
- 20. Thermodynamic Analysis SOUMYTH 20 Thermalefficiency of dual cycle: ηt Dual = wnet qin = 1 − qout qin = 1 − cv T4 − T1 cv Tx − T2 + cp T3 − Tx ηt Dual = 1 − T4 − T1 Tx − T2 + γ ⋅ T3 − Tx ηt dual = 1 − 1 rc k−1 ⋅ α ⋅ βγ − 1 γ ⋅ α β − 1 + α − 1 α → pressure ratio, rc → compression ratio, β = compression ratio
- 21. Comparison of Otto,Diesel and Dual Cycles SOUMYTH 21 For the same Inlet conditions, the same compression ratios and same Heat removal. Area under the T-s graph is equal to Heat transfer. So, qout is same for 3 cycles. But, qin is different. qin otto > qin dual > qin diesel 𝛈𝐭 𝐨𝐭𝐭𝐨 > 𝛈𝐭 𝐝𝐮𝐚𝐥 > 𝛈𝐭 𝐝𝐢𝐞𝐬𝐞𝐥 This is not a fair comparison because, as Compression ratio(rc) of Diesel and Dual cycles are much higher than Otto cycle.
- 22. Comparison of Otto,Diesel and Dual Cycles SOUMYTH 22 For the same inlet conditions, same peak pressure and same Heat removal. qin Diesel > qin dual > qin Otto 𝛈𝐭 𝐃𝐢𝐞𝐬𝐞𝐥 > 𝛈𝐭 𝐝𝐮𝐚𝐥 > 𝛈𝐭 𝐎𝐭𝐭𝐨
- 23. Comparison of Otto,Diesel and Dual Cycles SOUMYTH 23 For the same Inlet conditions and Heat addition and compression ratio. Otto cycle 1→2→3→4→1 Diesel cycle 1→2→3’→4’ →1 Dual cycle 1→2→2’ →3’’→4’’ →1 qout otto < qin dual < qin diesel 𝛈𝐭 𝐨𝐭𝐭𝐨 > 𝛈𝐭 𝐝𝐮𝐚𝐥 > 𝛈𝐭 𝐝𝐢𝐞𝐬𝐞𝐥
- 24. Stirling cycle SOUMYTH 24 •The Carnot cycle has a low mean effective pressure because of its very low work output. • Hence, one of the modified forms of the cycle to produce higher mean effective pressure whilst theoretically achieving full Carnot cycle efficiency is the Stirling cycle. • It consists of two isothermal and two constant volume processes.
- 25. Ericsson Cycle SOUMYTH 25 •The Ericsson cycle consists of two isothermal and two constant pressure processes. • The heat addition and rejection take place at constant pressure as well as isothermal processes • The advantage of the Ericsson cycle over the Carnot and Stirling cycles is its smaller pressure ratio for a given ratio of maximum to minimum specific volume with higher mean effective pressure.
- 26. Lenoir cycle SOUMYTH 26 •The Lenoir cycle consists of the following processes. Constant volume heat addition (1→2); isentropic expansion (2→3); constant pressure heat rejection (3→1). The Lenoir cycle is used for pulse jet engines.
- 27. Atkinson cycle SOUMYTH 27 •Atkinson cycle is an ideal cycle for Otto engine exhausting to a gas turbine. • In this cycle the isentropic expansion (3→4) of an Otto cycle (1234) is further allowed to proceed to the lowest cycle pressure so as to increase the work output. With this modification the cycle is known as Atkinson cycle.