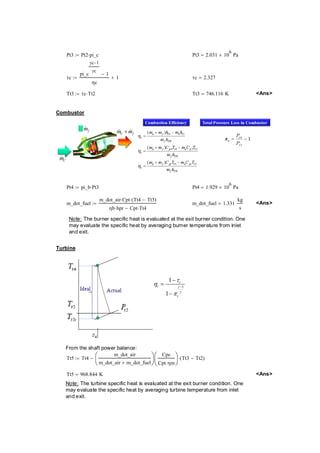
The document covers the analysis of an actual turbojet cycle, detailing various components' performance such as the compressor, burner, turbine, and nozzle under specific operating conditions. It includes calculations related to isentropic efficiency, thrust, and fuel mass flow rate, among others, while providing parameters and assumptions necessary for the analysis. Additionally, it discusses the potential improvements from switching to a variable converging-diverging nozzle, concluding that the marginal benefits may not justify the increased complexity and cost.

1. Aeropropulsion
Unit
Non-Ideal Cycle Analysis
2005 - 2010
International School of Engineering, Chulalongkorn University
Regular Program and International Double Degree Program, Kasetsart University
Assist. Prof. Anurak Atthasit, Ph.D.

2. Aeropropulsion
Unit Kasetsart University A. ATTHASIT 2
Actual Turbojet Cycle
In-class Practice: Ch06P01
0 1 2 3 4 5 9
0 m
f m
0
f
m
m
A turbojet flies at sea level at a Mach number of 0.75. It ingests
74.83 kg/s of air. The compressor operates with a pressure ratio
of 15 and an efficiency of 88 percent. The fuel has a heating
value of 41,400 kJ/kg, and the burner total temperature is
1389K. The burner has an efficiency of 91 percent and a total
pressure ratio of 0.95, whereas the turbine has an efficiency of
85 percent. A converging nozzle is used, and the nozzle
efficiency is 96 percent. The total pressure recovery for the
diffuser is 0.92 and the shaft efficiency is 99.5 percent. Find:
1. Isentropic diffuser efficiency
2. Compressor exit total temperature and pressure
3. Fuel mass flow rate
4. Turbine exit total temperature and pressure
5. Check if the nozzle is choked and find the nozzle exit area
6. The developed thrust
7. TSFC.
Prove
• Obj: Able to
use the
fundamental
equation
under the
correct
assumptions
Analysis
• Obj:
Understand
the physical
meaning of
each
parameters
Calculation
• Obj: Able to
solve the
relations
under the
constraints of
corrected unit,
constant, …
etc.
Standard Sea Level:
T0=288.2 K
P0=101.33 kPa
gc=1.4, gt=1.3
Cpc=1.004 kJ/kg/K
Cpt=1.239 kJ/kg/K

3. Actual Turbojet Cycle In-class Practice: Ch06P01
A turbojet flies at sea level at a Mach number of 0.75. It ingests 74.83 kg/s of air. The compressor
operates with a pressure ratio of 15 and an efficiency of 88 percent. The fuel has a heating value of
41,400 kJ/kg, and the burner total temperature is 1389K. The burner has an efficiency of 91 percent and
a total pressure ratio of 0.95, whereas the turbine has an efficiency of 85 percent. A converging nozzle
is used, and the nozzle efficiency is 96 percent. The total pressure recovery for the diffuser is 0.92 and
the shaft efficiency is 99.5 percent. Find:
1. Isentropic diffuser efficiency
2. Compressor exit total temperature and pressure
3. The fuel mass flow rate
4. Turbine exit total temperature and pressure
5. Check if the nozzle is choked and find the nozzle exit area
6. The developed thrust
7. TSFC
Constants Properties of Air and Hot gaz:
Cold Section: γc := 1.4 Cpc 1.004⋅103 J
kg K ⋅
:= Rc 287.1
J
kg K ⋅
:=
Hot Section: γt 1.4 := Cpt 1.00410⋅ 3 J
kg K ⋅
:= Rt 287.1
J
kg K ⋅
:=
Temp and Pressure at Standard Sea Level:
T0 288.2K :=
P0 101.3310:= ⋅ 3Pa
a0 γc Rc := ⋅ ⋅T0
Flight Condition and Engine Operations:
M1 0.75 :=
u1 M1a0 := ⋅
pi_c 15 :=
m_dot_air 74.83
kg
s
:=
Component Performance:
Diffuser pressure recovery factor:Fuel Characterisitc:
pi_d 0.92 := hpr 4140010⋅ 3 J
kg
:=
Compressor isentropic efficiency:
ηc 0.88 :=
Total pressure ratio of the burner:The mechanical shaft efficiency:
pi_b 0.95 := ηm 0.995 :=
Combustion efficiency:Isentropic turbine efficiency:
ηb 0.91 := ηt 0.85 :=
Maximum Total Temperature at Turbine inletNozzle efficiency:
Tt4 1389K := ηn 0.96 :=

4. Solutions:
Diffuser
τr 1
γc − 1
2
:= + ⋅M12 τr 1.113 =
pi_r τr
γc
γc−1
:= pi_r 1.452 =
Tt1 τr T0 := ⋅ Tt1 320.623K =
Pt1 pi_rP0 := ⋅ Pt1 1.47210= × 5 Pa
Note: Since the diffuser is adiabatic, the total temperature at the diffuser exit is
Tt2 Tt1 :=
Pressure recovery factor for the diffuser is
0.92;
Pt2
Pt1
=0.92
Pt2 pi_dPt1 := ⋅ Pt2 1.35410= × 5 Pa
Isentropic Efficiency of Diffuser is
ηd
τr pi_d
γc−1
⋅ γc − 1
τr − 1
:= ηd 0.767 = <Ans>
Compressor

5. Pt3 := Pt2⋅pi_c Pt3 2.03110= × 6 Pa
τc
pi_c
γc−1
γc − 1
ηc
:= + 1 τc 2.327 =
Tt3 τc Tt2 := ⋅ Tt3 746.116K = <Ans>
Combustor
C m
f m
C f m +m
Pt4 pi_bPt3 := ⋅ Pt4 1.92910= × 6 Pa
m_dot_fuel
m_dot_air Cpt ⋅ Tt4 Tt3 ⋅( − )
ηb hpr ⋅ Cpt Tt4 − ⋅
:= m_dot_fuel 1.331
kg
s
= Ans
Note: The burner specific heat is evaluated at the exit burner condition. One
may evaluate the specific heat by averaging burner temperature from inlet
and exit.
Turbine
1
1
1
t
t
t
γ
γ
τ
η
π
−
−
=
−
From the shaft power balance:
Tt5 Tt4
m_dot_air
m_dot_air m_dot_fuel +
⎛⎜⎝⎞⎟⎠
Cpc
Cpt⋅ηm
⎛⎜⎝
⎞⎟⎠
Tt3 Tt2 := − ⋅( − )
Tt5 968.844K = Ans
Note: The turbine specific heat is evaluated at the exit burner condition. One
may evaluate the specific heat by averaging turbine temperature from inlet
and exit.

6. To obtain Pt5, we must calculate Tt5i (Isentropic Total Temp.) and then use the
isentropic relation between temperature and pressure ratio.
pi_t 1
1
Tt5
Tt4
− ⎛⎜⎝
⎞⎟⎠
ηt
−
⎡⎢⎢⎣
⎤⎥⎥⎦
γt
γt−1
:= pi_t 0.214 =
Pt5 Pt4pi_t := ⋅ Pt5 4.13810= × 5 Pa Ans
Nozzle
Recall for the choked converging nozzle condition:
5 9
5 9
5 9 95
5 9 95
9 5 95959
9
5
1 / ( )
1 /
Applying the energy equation between states t5 and 9
2( )2()2()
Since the flow is still considered to be adiabatic,
t
n
t i
t t
n
t i it
t t nti
t
h h
h h
T T TT A
T T TT
u h hCpTTCpTT
T
T
η
η
η
−
=
−
− −
= =
− −
= − =−=−
9
9 2
9
1
2
1 9
9 9
5 5
* 1
9
5
1 ( ) 1 1
2
For the ideal case,
1 1 1 1
2
Sonic condition at nozzle exit (choked converging nozzle),
1 1
(1 )
t
n
i
t t n
t n
T B
T M
P T M
P T
P
P
γ
γ
γ
γ
γ
γ
γ
η
γ
η
γ
η γ
−
−
−
⎛ ⎞
⎜ ⎟
= = ⎜ ⎟ ⎜ − ⎟ +
⎝ ⎠
⎛ − + ⎞ ⎜ − ⎟
⎛ ⎞ ⎜ + ⎟
= ⎜ ⎟ = ⎜ ⎟
⎝ ⎠ ⎜ ⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎛ − ⎞
= ⎜ + ⎟ ⎝ + ⎠
Note that, the nozzle is choked when P9P0 which gives the result of M9=1 Ans
P9_sonic Pt51
1 − γt
ηn⋅(1 + γt)
+ ⎡⎢⎣
⎤⎥⎦
γt
γt−1
:= ⋅ P9_sonic 2.12310= × 5 Pa
Then the nozzle is choked, and gives M9=1. From (B),

7. T9 Tt5
1
1
γt − 1
2
+
⎛⎜⎜⎝
⎞⎟⎟⎠
:= ⋅ T9 807.37K =
u9 2Cpt ⋅ Tt5 T9 := ⋅( − ) u9 569.421
m
s
=
ρ9
P9_sonic
Rt T9 ⋅
:= ρ9 0.916
kg
m3
=
A9
m_dot_fuel m_dot_air ( + )
ρ9 u9 ⋅
:= A9 0.146m= 2 Ans
Total Thrust:
Thrust_momentum m_dot_fuelm_dot_air ( + ) u9 ⋅ m_dot_air u1 := − ⋅
Thrust_pressure A9P9_sonicP0 := ⋅( − )
Thrust Thrust_momentumThrust_pressure := +
Thrust_pressure 1.62110= × 4 N
Thrust 4.04710= × 4 N Ans
TSFC:
TSFC
m_dot_fuel
Thrust
:= TSFC 3.28910 − 5 × s
m
= Ans

8. Aeropropulsion
Unit Kasetsart University A. ATTHASIT 3
Actual Turbojet Cycle
Influence of Nozzle Area
In-class Practice: Ch06P02
Prove
• Obj: Able to
use the
fundamental
equation
under the
correct
assumptions
Analysis
• Obj:
Understand
the physical
meaning of
each
parameters
Calculation
• Obj: Able to
solve the
relations
under the
constraints of
corrected unit,
constant, …
etc.
0 1 2 3 4 5 9
0 m
f m
0
f
m
m
To improve the engine performance, one can replace
the converging nozzle with a variable converging-diverging
nozzle (to match the exit pressure to the
ambient pressure) and repeat the preceding
calculations to see how much improvement results.
All of the computations are the same as those in
Ch06P01 up to the nozzle. Find:
1. Gas exit Mach number and the nozzle exit area
2. The developed thrust
3. TSFC.
Standard Sea Level:
T0=288.2 K
P0=101.33 kPa
gc=1.4, gt=1.3
Cpc=1.004 kJ/kg/K
Cpt=1.239 kJ/kg/K

9. Actual Turbojet CycleInfluence of Nozzle Area
In-class Practice: Ch06P02
To improve the engine performance, one can replace the converging nozzle with a variable
converging-diverging nozzle (to match the exit pressure to the ambient pressure) and repeat the
preceding calculations to see how much improvement results. All of the computations are the
same as those in Ch06P01 up to the nozzle. Find:
1. Gas exit Mach number and the nozzle exit area
2. The developed thrust 3. TSFC.
Results from Ch06P01
Constants Properties of Air and Hot gaz:
Cold Section: γc := 1.4 Cpc 1.004⋅103 J
kg K ⋅
:= Rc 287.1
J
kg K ⋅
:=
Hot Section: γt 1.4 := Cpt 1.00410⋅ 3 J
kg K ⋅
:= Rt 287.1
J
kg K ⋅
:=
Temp and Pressure at Standard Sea Level:
T0 288.2K :=
P0 101.3310:= ⋅ 3Pa
a0 γc Rc := ⋅ ⋅T0
Turbine exit:
Tt5 968.844K :=
Pt5 4.13810:= ⋅ 5Pa
Component Performance:
Nozzle efficiency:
ηn 0.96 :=
Mass Flow Rate:
m_dot_fuel 1.331
kg
s
:=
m_dot_air 74.83
kg
s
:=
Flight Condition and Engine Operations:
M1 0.75 :=
u1 M1a0 := ⋅

10. Solutions
The nozzle is variable nozzle, and so the exit pressure matches the ambient pressure and
there is no need to check for choking
P9 P0 :=
T9i Tt5
P9
Pt5
⎛⎜⎝
⎞⎟⎠
γt−1
γt
:= ⋅ T9i 648.138K =
The nozzle efficiency is again 96 percent, thus, the nozzle exit temperature is
T9 Tt5 ηn Tt5T9i := − ⋅( − ) T9 660.966K =
The exit speed can obtain from the energy equation,
u9 2Cpt ⋅ Tt5 T9 := ⋅( − ) u9 786.269
m
s
=
a9 γt Rt := ⋅ ⋅T9 a9 515.431
m
s
=
M9
u9
a9
:= M9 1.525 = Ans
Note: the hot gas exit velocity is much higher than one of the choked case (Ch06P01).
ρ9
P9
Rt T9 ⋅
:= ρ9 0.534
kg
m3
=
A9
m_dot_fuel m_dot_air ( + )
ρ9 u9 ⋅
:= A9 0.181m= 2 Ans
Note: The Nozzle exit area is slightly higher than one of the choked case.
Total Thrust:
Thrust_momentum m_dot_fuelm_dot_air ( + ) u9 ⋅ m_dot_air u1 := − ⋅
Thrust_pressure A9P9P0 := ⋅( − )
Thrust Thrust_momentumThrust_pressure := +
Thrust_momentum 4.07810= × 4 N
Thrust_pressure 0N =
Thrust 4.07810= × 4 N Ans
TSFC:
TSFC
m_dot_fuel
Thrust
:= TSFC 3.26410 − 5 × s
m
= Ans

11. Aeropropulsion
Unit
Kasetsart University
4
A. ATTHASIT
Influence of Nozzle Area In-class Practice: Ch06P03
Prove
•Obj: Able to use the fundamental equation under the correct assumptions
Analysis
•Obj: Understand the physical meaning of each parameters
Calculation
•Obj: Able to solve the relations under the constraints of corrected unit, constant, … etc.
As one can see for this operating point, the results are only marginally better. Consequently, for this particular design one would probably not add the complexity and cost of a variable converging- diverging nozzle for the small improvement that would result.

12. Aeropropulsion
Unit Kasetsart University A. ATTHASIT 5
Conclusion
*
2
1
*
2
1
1
*
*
2
*
1
2( 1)
2
*
1
2
1
1
2
1
2
1
1
2
1
2
1
1
2
1
1
1 2
1
2
T
T
M
P
P
M
P
P
T
M
T
P
m AV AM
R T
M
A
A M
g
g
g
g
g
g
g
g
g
g

 g
g

g
g






  
 
 
  
 
  
           
  
 
   
           
 
    
    
    
  
 
 
2
0
0 t
dA d du
A u
udu dP
dh dh udu
dP d dT
P T
a
P






g
  
 
  
 

P dP
T dT
d
A dA
u du
 





P
T
A
u

dx
2
dP
P 
See You
Next Class!