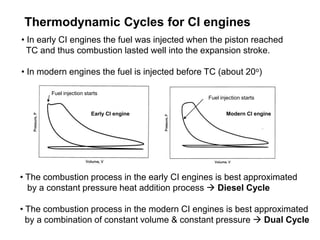
Thermodynamic Cycles for CI engines - Early CI engines injected fuel at top dead center, resulting in combustion during the expansion stroke. Modern engines inject fuel before top dead center, around 20 degrees. - The combustion process in early CI engines approximates a constant pressure heat addition process, known as the Diesel cycle. Modern CI engines' combustion approximates a combination of constant volume and constant pressure processes, known as the Dual cycle. - The air-standard Diesel cycle consists of four processes: isentropic compression, constant pressure heat addition, isentropic expansion, and constant volume heat rejection. Its thermal efficiency is lower than the Otto cycle for the same compression ratio due to the later fuel injection

1. Thermodynamic Cycles for CI engines
• In early CI engines the fuel was injected when the piston reached
TC and thus combustion lasted well into the expansion stroke.
• In modern engines the fuel is injected before TC (about 20o)
Fuel injection starts
Early CI engine
Fuel injection starts
Modern CI engine
• The combustion process in the early CI engines is best approximated
by a constant pressure heat addition process  Diesel Cycle
• The combustion process in the modern CI engines is best approximated
by a combination of constant volume & constant pressure  Dual Cycle

2. Early CI Engine Cycle vs Diesel Cycle
FUEL
A
Fuel injected
at TC
I
R
Fuel/Air
Mixture
Combustion
Products
Actual
Cycle
Intake
Stroke
Compression
Stroke
Power
Stroke
Qin
Diesel
Cycle
Air
Exhaust
Stroke
Qout
TC
BC
Compression
Process
Const pressure
heat addition
Process
Expansion
Process
Const volume
heat rejection
Process

3. Air-Standard Diesel Cycle
Process 1 2
Process 2  3
Process 3  4
Process 4  1
Isentropic compression
Constant pressure heat addition
Isentropic expansion
Constant volume heat rejection
Cut-off ratio:
Qin
rc
Qout
v2
TC
v1
BC
TC
BC
v3
v2

4. First Law Analysis of Diesel Cycle
Equations for processes 12, 41 are the
same as those presented for the Otto cycle
23 Constant Pressure Heat Addition
(
Qin
m
P3v3 ) (u 2
Qin
m
(h3
Qin
Qin
P V V2
) 2 3
m
m
(u3 u 2 )
(u3
AIR
h2 )
P2 v2 )
P
RT2
v2
RT3
v3
T3
T2
v3
v2
rc

5. 3  4 Isentropic Expansion
(u 4 u3 )
Wout
m
vr4
vr3
P4 v4
T4
Wout
Q
(
)
m
m
AIR
(u3 u 4 )
v4
v4
note v4=v1 so
v3
v3
P3v3
T3
P4
P3
T4 r
T3 rc
v4 v2
v2 v3
v1 v2
v2 v3
vr
r

rc
vr
4
3
v4
v3
r
rc

6. Thermal Efficiency
Diesel
cycle
1
Qout m
u u
1 4 1
Qin m
h3 h2
For cold air-standard the above reduces to:
Diesel
const cV
1
1
r
k 1
1 rck 1
k rc 1
recall,
Otto
1
1
rk
1
Note the term in the square bracket is always larger than one so
for the same compression ratio, r, the Diesel cycle has a lower
thermal efficiency than the Otto cycle
When rc (=v3/v2)1 the Diesel cycle efficiency approaches the
efficiency of the Otto cycle

7. Thermal Efficiency
Modern CI Engines
12 < r < 23
The cut-off ratio is not a natural choice for the independent variable
A more suitable parameter is the heat input, the two are related by:
rc
1
k 1 Qin
1
k P V1 r k 1
1
as Qin 0, rc1 and

Otto