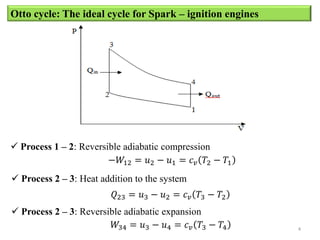
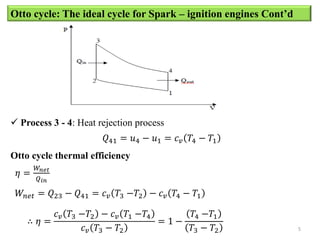
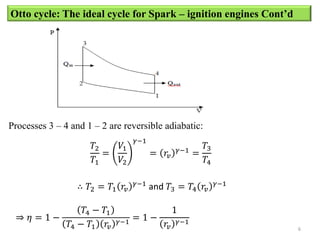
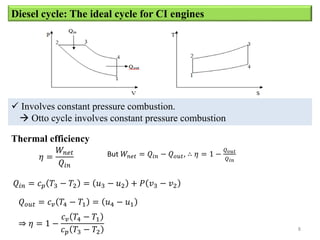
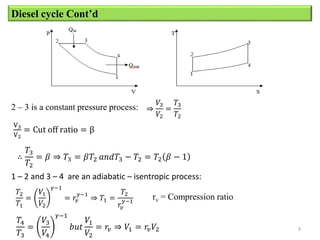
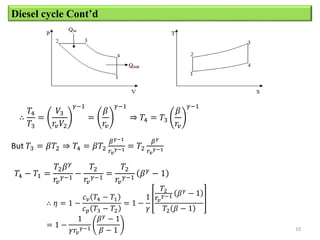
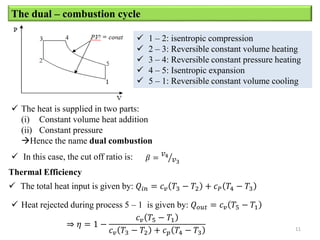
The document provides an overview of different types of reciprocating engine cycles, including definitions of key terms, equations, and efficiency calculations. It describes the ideal Otto, Diesel, and dual combustion cycles. It includes equations to calculate efficiency, temperatures, pressures, work output, and mean effective pressure. It concludes with sample problems to calculate values for each cycle type.